基于RBF神经网络的AUV路径跟踪分数阶滑模控制

王 香, 张永林

基于RBF神经网络的AUV路径跟踪分数阶滑模控制

王 香, 张永林

(江苏科技大学 电子信息学院, 江苏 镇江, 212003)

针对自主水下航行器(AUV)在对接过程中的路径跟踪问题, 提出一种基于径向基函数(RBF)神经网络的分数阶滑模控制算法。首先基于滑模控制设计AUV路径跟踪控制算法, 将分数阶微积分引入滑模控制中的等速趋近律以缓解系统的抖振, 然后采用RBF神经网络对AUV运动模型中的不确定性及外界干扰进行补偿, 最后通过Lyapunov定理证明了控制系统的稳定性。仿真结果表明: 所设计的控制器能对AUV路径进行有效跟踪, 与传统滑模控制器以及未考虑系统不确定性及外界干扰的分数阶滑模控制器相比, 该控制器跟踪速度更快, 稳定效果更好, 跟踪性能更强。

自主水下航行器; 路径跟踪; 径向基函数神经网络; 滑模控制; 分数阶微积分

0 引言

随着人类对海洋资源不断地开发利用, 自主水下航行器(autonomous undersea vehicle, AUV)成为了探索海洋的重要载体, 而精准的路径跟踪能力是AUV水下作业能力的技术保障之一[1-4]。海洋环境极其复杂并且充满不确定性, 在实际运行中, 由于其强非线性、不确定性、多耦合性等特点, 当运行速度及运行环境发生改变时, AUV所受到的水动力、惯性力和科里奥利向心力等会随之发生改变, 很难建立精准的动力学模型对其轨迹进行跟踪[5-9]。

目前, 模糊控制、自适应鲁棒控制、反步法和神经网络等控制方法均被用于AUV的运动控制。文献[10]提出一种反步法与滑模控制相结合的变深控制方法抑制无人水下航行器(unmanned undersea vehicle, UUV)运动过程中的姿态失衡问题。文献[11]利用神经网络控制器补偿水下机器人受到的环境干扰, 设计了一种基于反步滑模控制的AUV变深控制算法, 解决了离散AUV水平面的路径跟踪控制问题。文献[12]提出一种基于模糊滑模的AUV深度控制器, 有效抑制了传统滑模控制中的抖振问题。目前, 对AUV精准路径跟踪问题的研究仍是AUV研究领域的热点之一。

分数阶微积分是整数阶微积分的推广, 近年来, 基于分数阶微积分与滑模控制理论而产生的分数阶滑模控制已取得了一些进展。文献[13]提出了一种基于分数阶微积分的机械臂滑模控制算法, 有效的提高了关节的跟踪速度与跟踪精度。文献[14]提出了集成神经网络与自适应算法的分数阶滑模控制。文献[15]提出了一种神经网络结合干扰观测器的主动反馈控制方法, 以解决异结构不确定分数阶混沌系统的同步问题。文章在现阶段研究基础上, 提出了一种新型的基于径向基函数(radial basis function, RBF)神经网络的分数阶滑模控制。在利用滑模控制对AUV进行路径跟踪的基础上, 将分数阶微积分引入滑模控制的等速趋近律中来缓解系统的抖振, 并采用RBF神经网络补偿AUV动力学模型中的不确定性以及外部未知干扰, 利用 Lyapunov函数证明了系统的稳定性。与传统的滑模控制[16]及分数阶滑模控制[13]路径跟踪效果相比较, 文中采用的控制方法跟踪时间快, 跟踪性能好, 能有效补偿系统的不确定性以及外部扰动。

1 AUV数学模型

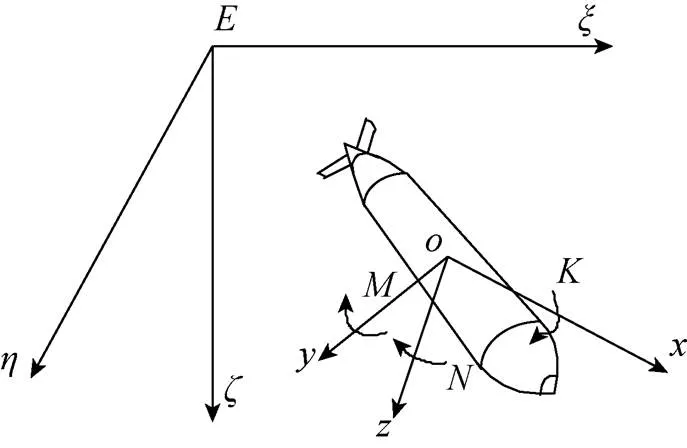
图1 AUV运动坐标系

在运动坐标系下, 可将AUV的六自由度动力学模型描述为[17]

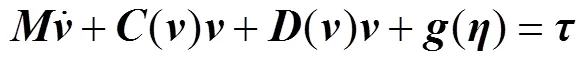
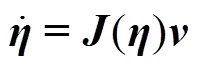
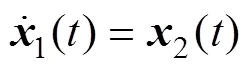
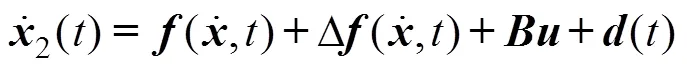
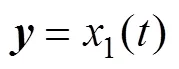
2 基于RBF神经网络的分数阶滑模控制

针对AUV模型不确定性和外界干扰对其运动控制和路径跟踪精度的影响, 以及传统滑模存在的抖振问题, 文中提出了一种基于RBF神经网络的分数阶滑模控制算法, 其结构图如图2所示。主要利用滑模控制对AUV期望路径进行跟踪控制, 同时利用分数阶微积分修正滑模控制中等速趋近律的参数来缓解系统的抖振, 并且将RBF神经网络用于补偿AUV动力学模型中的不确定性及外界不确定干扰, 从而达到对AUV精确跟踪的效果。

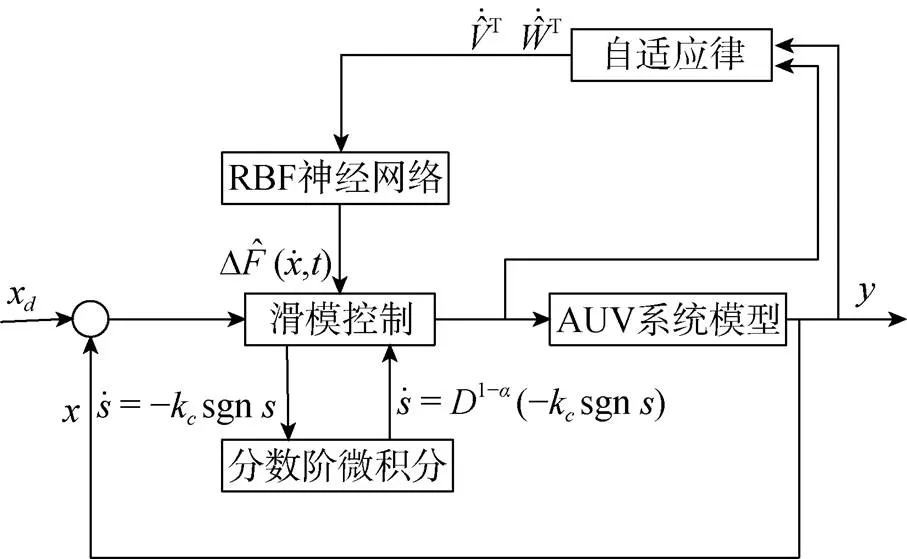
图2 控制系统结构图

2.1 分数阶滑模控制

分数阶微积分由整数阶微积分衍生而来, 扩展了微积分阶次的概念, 其算子定义为

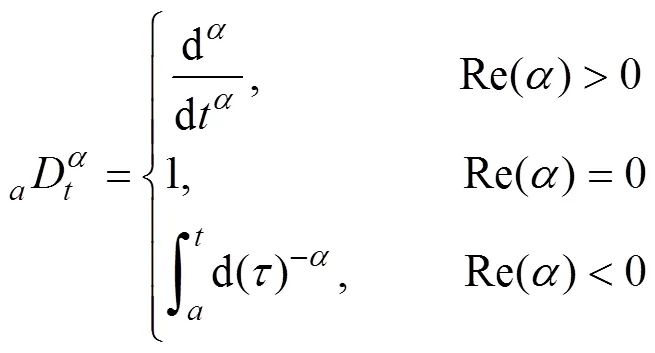
Caputo分数阶积分定义为

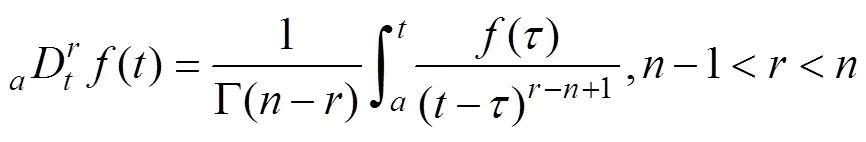
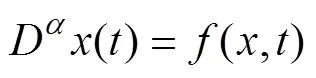
假设Lyapunov函数满足如下条件

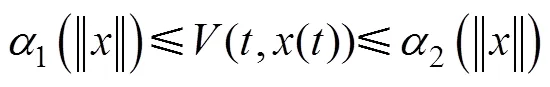
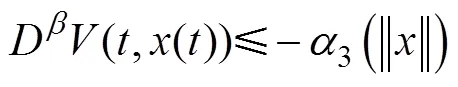
将上述分数阶积分算子引入滑模控制中, 跟踪误差表达式为

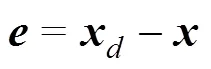
设计滑模面为

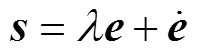
对其进行求导, 可得

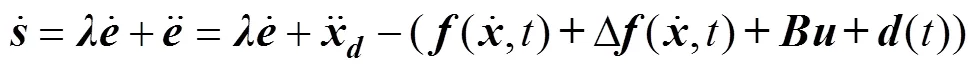
在滑模控制中一般采用趋近律的方法改善趋近运动过程中的动态品质[21], 但传统趋近律存在抖振严重和收敛时间长等缺点, 故文中将分数阶微积分引入等速趋近律中, 选取了一种分数阶趋近律。

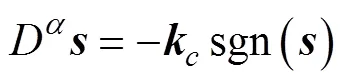
则

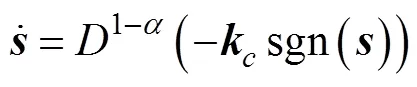
采用以下Lyapunov函数

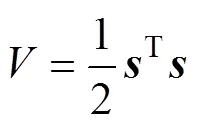
对式(16)两端进行求导, 得

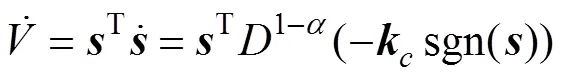
由于

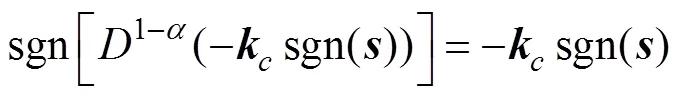
则

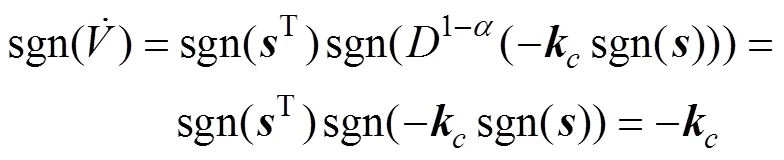
对于带有模型不确定性及外界干扰的系统, 设计控制输入为

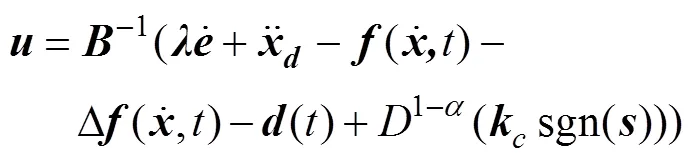
2.2 基于RBF神经网络的分数阶滑模控制

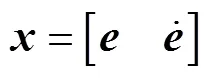
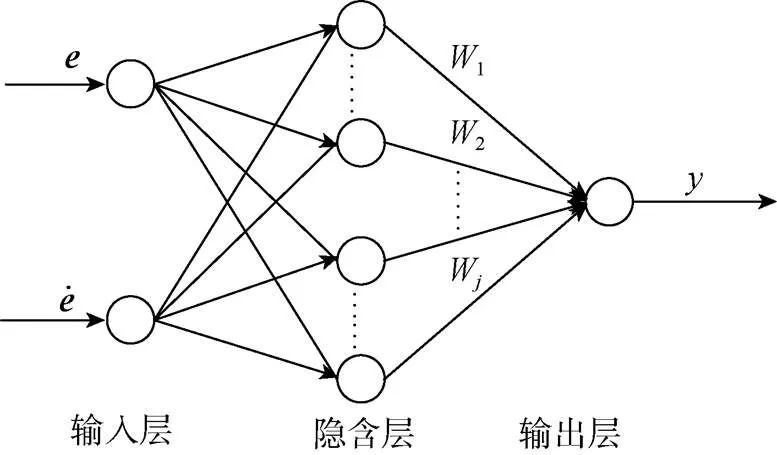
图3 RBF神经网络拓扑结构

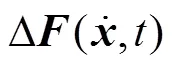
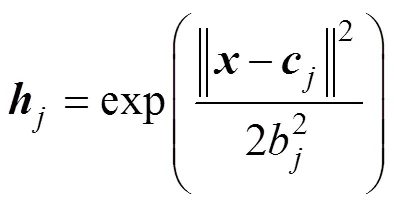
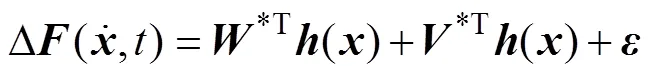
网络输出为

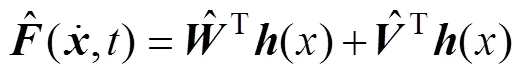
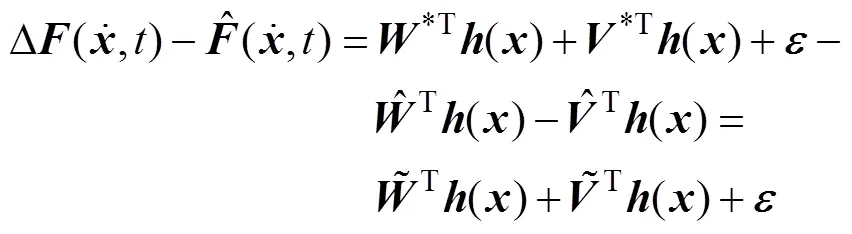
定义Lyapunov函数为

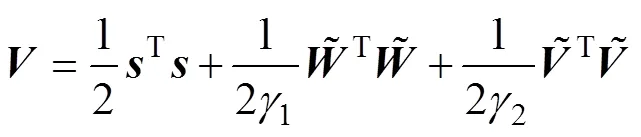
设计控制律为

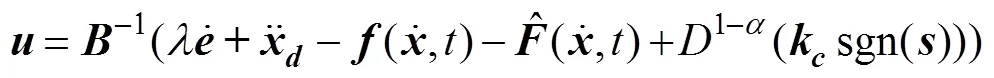
则

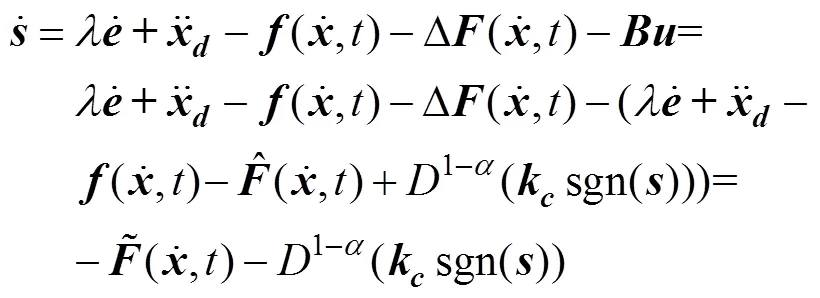
故

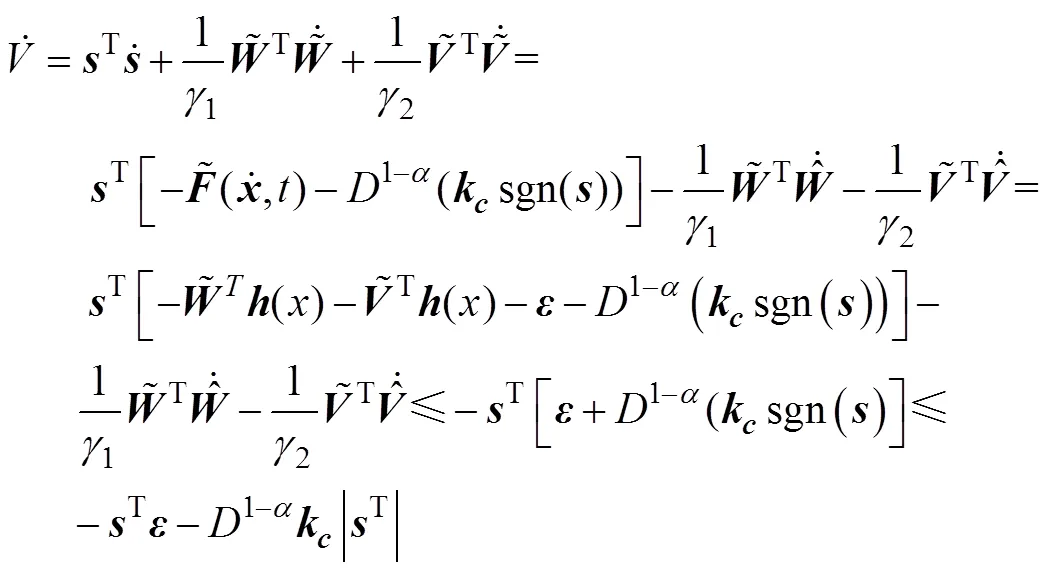
3 仿真结果与分析

为了验证文中所提方法的有效性和可靠性, 采用安装了分数阶建模与控制工具箱FOMCON的MATLAB来完成仿真。在AUV的运动过程中, 横滚方向的影响较小, 因此仅考虑前进、横移、升沉、纵倾和艏摇5个自由度的运动。

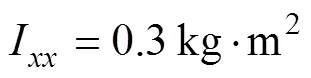
图4为文中所提控制方法的速度跟踪情况, 从图中可以看出, 各方向在轻微的抖动后都能很快地跟踪至期望速度。图5为文中所提控制方法各方向的控制输入, 可以看到各方向都有较好的控制状态。

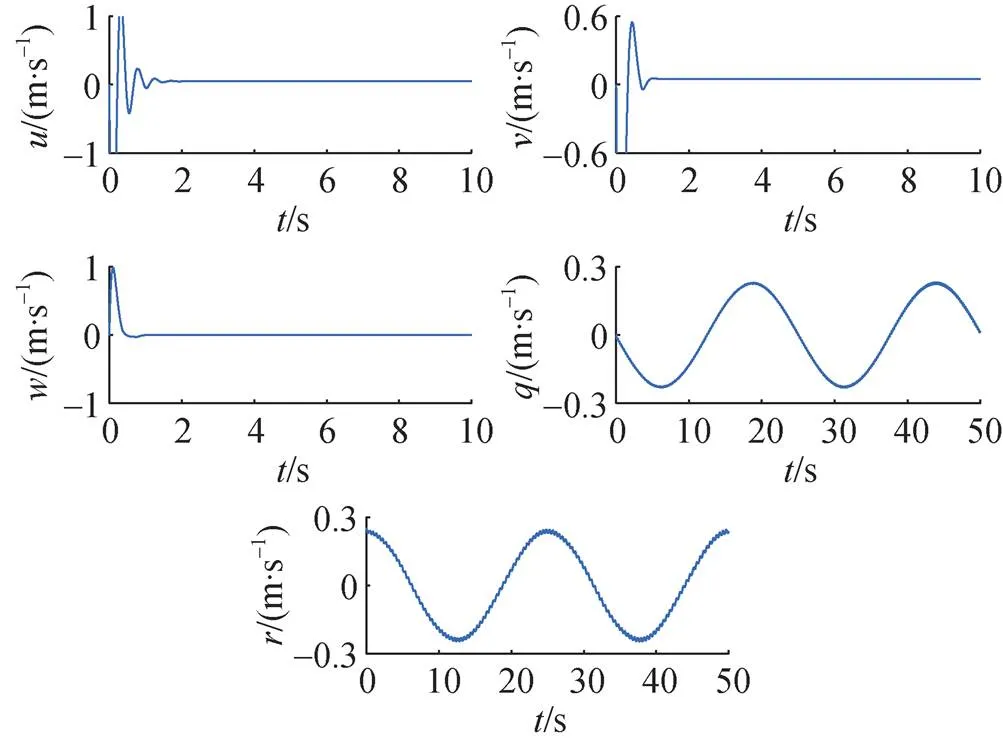
图4 各方向速度跟踪情况

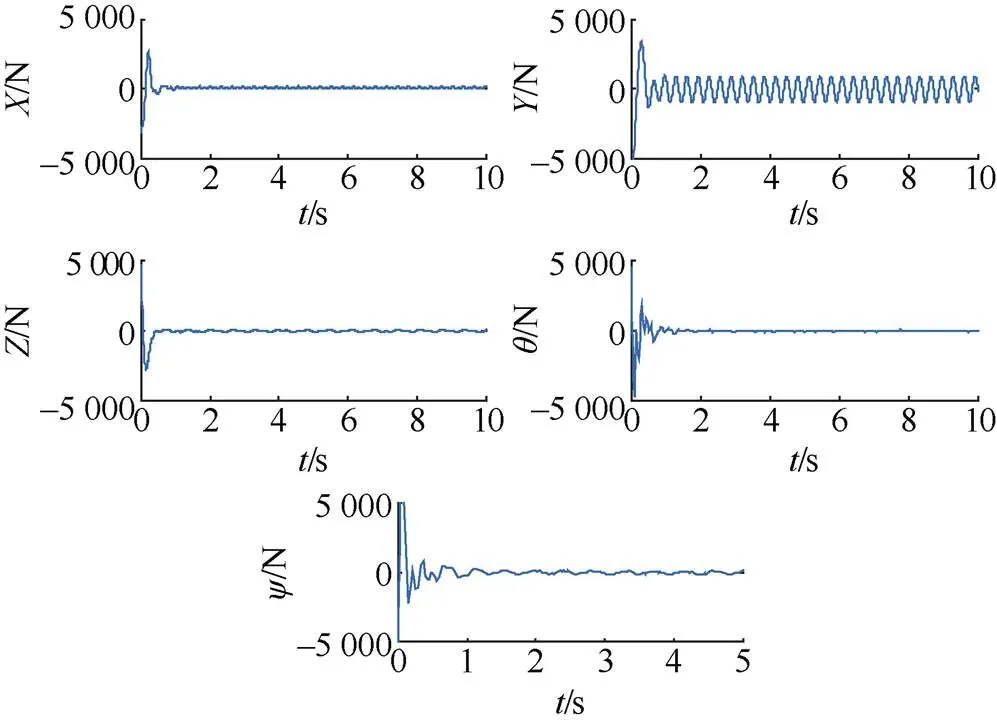
图5 各方向控制输入曲线

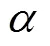
为进一步分析, 对图6~8中的数据进行处理, 处理结果如表1所示。

由表1可知, 文中所提控制方法与传统的等速趋近律滑模控制相比, 跟踪误差的均方差减小了45%, 平均绝对跟踪误差减小了62.5%; 与分数阶滑模控制的跟踪效果相比, 跟踪误差的均方差减小了11%, 平均绝对跟踪误差减小了25%。故该控制方法优于传统滑模控制与分数阶滑模控制, 具有实际应用价值。

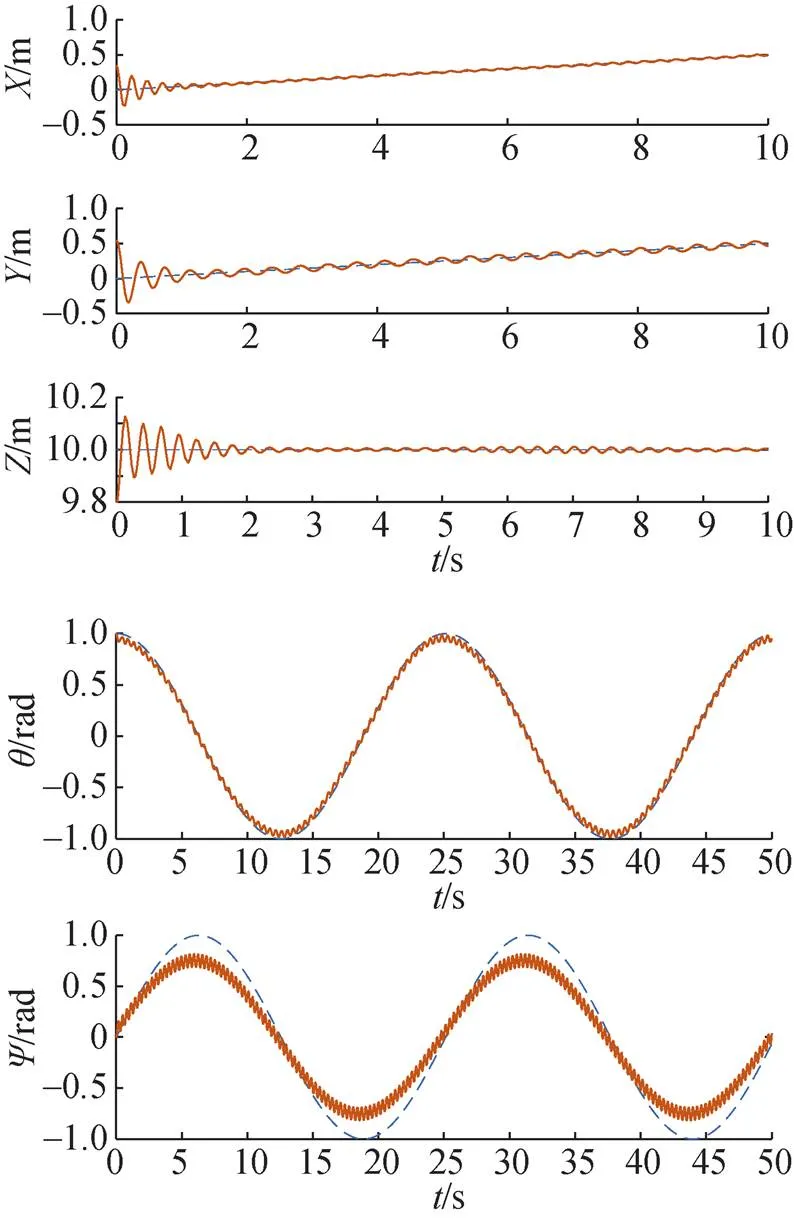
图6 基于传统滑模控制的AUV路径跟踪

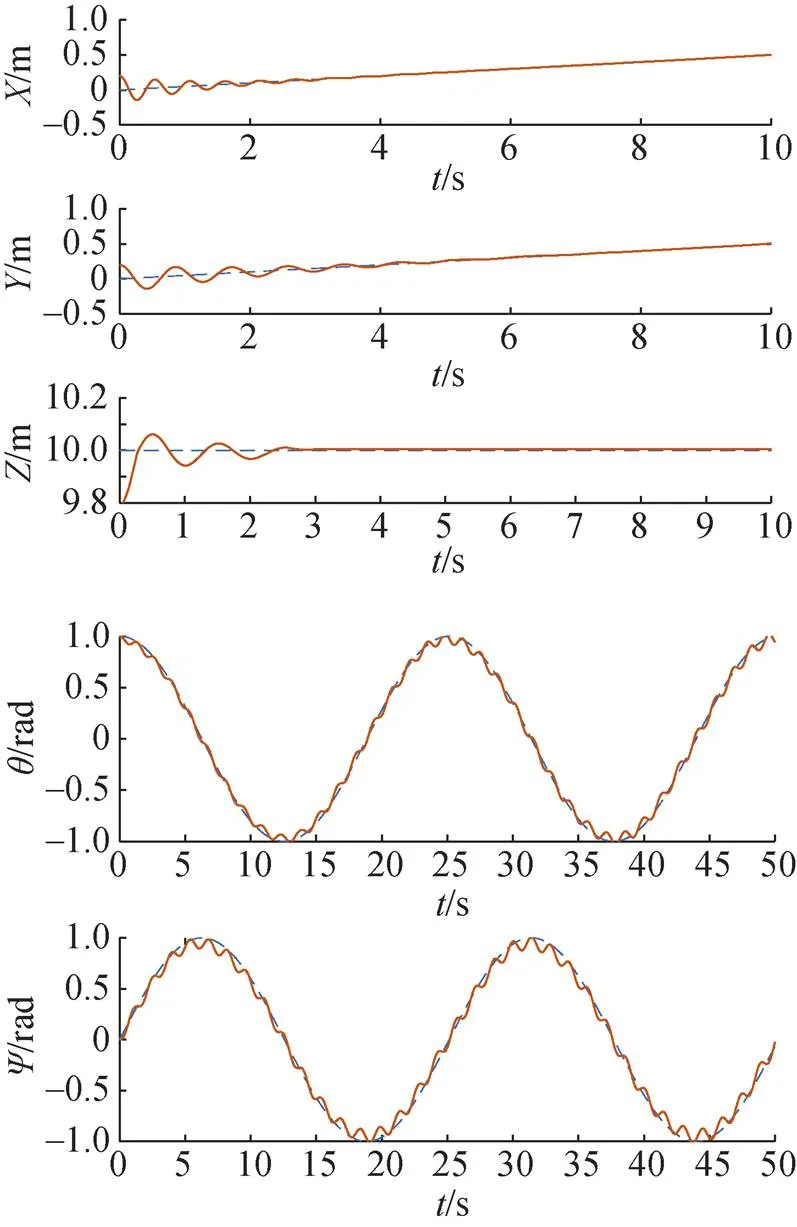
图7 基于分数阶滑模控制的AUV路径跟踪

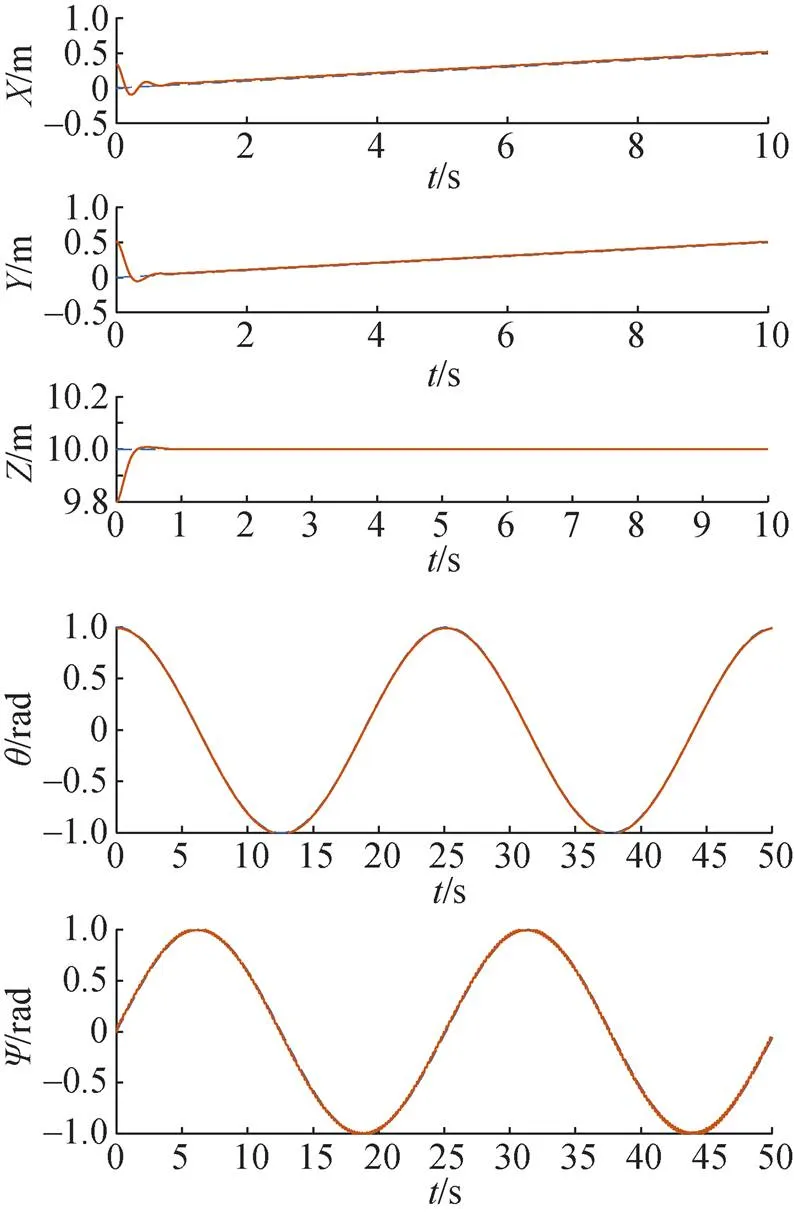
图8 基于RBF神经网络的AUV分数阶滑模路径跟踪

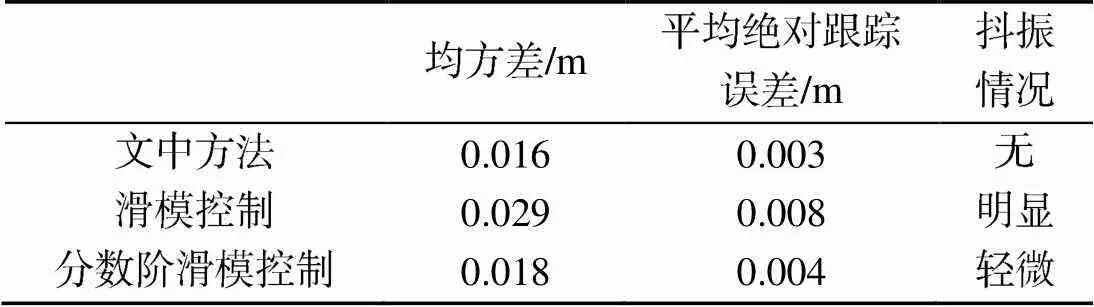
表1 不同控制方法跟踪数据对比

4 结束语

文中针对AUV的精准路径跟踪问题, 提出了一种基于RBF神经网络的AUV路径跟踪分数阶滑模控制方法。将分数阶微积分引入滑模控制的趋近律, 利用分数阶微积分修正滑模控制中等速趋近律的参数来消除系统的抖振, RBF神经网络用于补偿AUV动力学模型中的不确定性及外界不确定干扰, 并用Lyapunov定理证明了其稳定性。同时将提出的控制方法与单一的滑模控制及分数阶滑模控制的跟踪效果相比较, 得出了在相同条件下, 该控制方法具有更快的收敛时间和更好的跟踪性能, 更加适用于实际应用。

[1] 孙叶义, 武皓微, 李晔, 等. 智能无人水下航行器水下回收对接技术综述[J]. 哈尔滨工程大学学报, 2019, 40(1): 1-11.Sun Ye-yi, Wu Hao-wei, Li Ye, et al. Summary of AUV Underwater Recycle Docking Technology[J]. Journal of Harbin Engineering University, 2019, 40(1): 1-11.

[2] Palomeras N, Vallicrosa G, Mallios A, et al. AUV Homing and Docking for Remote Operations[J]. Ocean Engineering, 2018(154): 106-120.

[3] Petersen M J, Pedersen P T. Collision between Ships and Offshore Platform[C]//Proceeding of 13th Annual Offshore Technology Conference. Houston, US: OTC4134, 2011, 163-171.

[4] 史剑光, 李德骏, 杨灿军, 等. 水下自主机器人接驳碰撞过程分析[J]. 浙江大学学报(工学版), 2015, 49(3): 497-504.Shi Jian-guang, Li De-jun, Yang Can-jun, et al. Impact Analysis during Docking Process of Autonomous Underwater Vehicle[J]. Journal of Zhejiang University(Engi- neering Science), 2015, 49(3): 497-504.

[5] Mitra A, Panda J P, Warrior H V. The Effects of Free Stream Turbulence on the Hydrodynamic Characteristics of an AUV Hull Form[J]. Ocean Engineering, 2019(174): 148-158.

[6] Marani G, Choi S K, YUH.J. Underwater Autonomous Manipulation for Intervention Missions AUVs[J]. Ocean Engineering, 2009, 36(1): 15-23．

[7] 李岳明. 多功能自主式水下机器人运动控制研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

[8] Carlucho I, Paula M D, Wang S, et al. Adaptive Low- Level Control of Autonomous Underwater Vehicles Using Deep Reinforcement Learning[J]. Robotics and Autonomous Systems, 2018(107): 71-86

[9] Liang X, Wan L, Blake J, et al. Path Following of an Under Actuated AUV Based on Fuzzy Back-Stepping Sliding Mode Control[J]. International Journal of Advanced Robotic Systems, 2016, 13(122): 1-11.

[10] 蒋云彪, 郭晨, 于浩淼. 基于反步滑模算法的水下无人航行器变深控制[J]. 船舶工程, 2018, 40(2): 83-87.Jiang Yun-biao, Guo Chen, Yu Hao-miao. Diving Control of Unmanned Underwater Vehicle Based on Backstepping Sliding Model Algorithm[J]. Ship Engineering, 2018, 40(2): 83-87.

[11] 赵杰梅, 胡忠辉. 基于动态反馈的AUV水平面路径跟踪控制[J]. 浙江大学学报(工学版), 2018, 52(8): 1467- 1473, 1481.Zhao Jie-Mei, Hu Zhong-Hui. Path Following Control of AUV in Horizontal Plane Based on Dynamic Feedback Control[J]. Journal of Zhejiang University(Engineering Science), 2018, 52(8): 1467-1473, 1481.

[12] Lakhekar G, Deshpande R. Diving Control of Autonomous Underwater Vehicles via Fuzzy Sliding Mode Tech-nique[C]//International Conference on Circuit, Power and Computing Technologies. Jeju, South Korea: IEEE, 2015.

[13] 张鑫, 李嘉欣. 基于分数阶微积分的机械臂滑模控制的研究[J/OL]. 系统仿真学报, http://kns.cnki.net/kcms/de tail/11.3092.V.20190213.1217.016.html.

[14] 张碧陶, 高福荣, 姚科. 集成神经网络与自适应算法的分数阶滑模控制[J]. 控制理论与应用, 2016, 33(10): 1373-1377.Zhang Bi-tao, Gao Fu-rong, Yao Ke. Neural Network and Adaptive Algorithm-Based Fractional Order Sliding Mode Controller[J]. Control Theory & Applications, 2016, 33(10): 1373-1377.

[15] 程春蕊, 朱军辉, 王东晓. 分数阶不确定四翼混沌系统的自适应滑模同步[J]. 华中师范大学学报(自然科学版), 2018, 52(2): 155-159.Cheng Chun-rui, Zhu Jun-hui, Wang Dong-xiao. Adaptive Synchronization of Fractional-Order Four-Wings Chaotic Systems with Uncertainties Based on Sliding Mode Control[J]. Journal of HuaZhong Normal University(Natural Sciences), 2018, 52(2): 155-159.

[16] 何晓燕, 张永林. 水下遥作业系统的协调控制的研究[J]. 船舶工程, 2013, 35(3): 67-70.

[17] Källström C G. Guidance and Control of Ocean Vehicles[J]. Automatica, 1996, 32(8): 1235.

[18] Li Y, Chen Y, Podlubny I. Mittag-Leffler Stability of Fractional Order Nonlinear Dynamic Systems[J]. Automatica, 2009, 45(8): 1965-1969.

Fractional-Order Sliding Mode Control Based on RBF Neural Network for AUV Path Tracking

WANG Xiang, ZHANG Yong-lin

(School of Electronics and Information, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

Aiming at the path tracking problem of autonomous undersea vehicle(AUV) in the process of docking, a fractional-order sliding mode control algorithm based on radial basis function(RBF) neural network is proposed. Firstly, the AUV path tracking control algorithm is designed based on sliding mode control, the fractional calculus is introduced into the constant velocity reaching law of sliding mode control to alleviate the shaking of the system. Then, the RBF neural network is used to compensate for uncertainty in the AUV motion model and for external interference. Finally, the stability of the control system is proved by Lyapunov stability theory. Simulation results show that the designed controller can effectively track the path of AUV. Compared with the traditional sliding mode control and the fractional-order sliding mode control without considering system uncertainty and external interference, the proposed control method has faster tracking speed, higher stability and better tracking performance.

autonomous undersea vehicle(AUV); path tracking; radial basis function(RBF) neural network; sliding mode control; fractional calculus

TP273; TP242.2

A

2096-3920(2020)03-0284-07

10.11993/j.issn.2096-3920.2020.03.007

2018-12-06;

2019-01-04.

王 香(1995-), 女, 在读硕士, 主要研究方向为先进控制理论及应用.

王香, 张永林. 基于RBF神经网络的AUV路径跟踪分数阶滑模控制[J]. 水下无人系统学报, 2020, 28(3): 284-290.

(责任编辑: 陈 曦)