一种回溯算法结合数据时序重构融合滤波的初始对准方法

杨管金子, 李建辰, 国琳娜, 黄 海

一种回溯算法结合数据时序重构融合滤波的初始对准方法

杨管金子1, 2, 李建辰1, 2, 国琳娜1, 2, 黄 海1

(1. 中国船舶重工集团公司 第705研究所, 陕西 西安, 710077; 2. 水下信息与控制重点实验室, 陕西 西安, 710077)

为了在提高鱼雷初始对准精度的同时保证较短的对准时间, 文中在采用回溯算法进行初始对准的基础上, 通过对存储数据的调用及线下处理, 提出一种数据时序重构融合滤波算法, 通过对存储数据进行再次调用、整体辨识、特征量提取和时序重构, 构建多级滤波器, 与传统“正向—逆向—正向”滤波回溯算法比较, 实现了一定时间内滤波估计及对准精度的进一步提高。实航数据的仿真对比试验证明了该方法在精度及时间上的有效性。

鱼雷; 初始对准; 回溯算法; 时序重构; 融合滤波

0 引言

作为水下反舰反潜主战武器, 鱼雷需要具备快速发射和精确制导的作战能力, 初始对准作为惯性导航系统的关键技术之一, 直接影响鱼雷射前准备时间及水下导航定位精度。

为了在提高鱼雷对准精度的同时, 保证较短的对准时间, 国内外学者开展了大量的研究。高伟[1]、Acharya[2]等提出一种基于观测量扩充的捷联惯导系统快速对准方法, 在保证原有精度同时, 缩短了对准时间; 王岩等[3]提出一种贯序传递对准方案, 使得滤波器具有更快的估计收敛速度; 张磊等[4]提出多级组合滤波的思想, 实现了捷联惯导的快速初始对准(约30 s); Wang等[5]提出了二次对准技术方案。随着计算机技术的发展, 李京书等[6]提出了基于罗经法的严格正逆向迭代对准算法; Thompson[7]、张朝飞[8]、刘锡祥[9]等也分别对回溯算法进行了相应有效性的研究。

以上研究内容皆在一定程度上兼顾了初始对准精度及对准时间的双向指标, 特别是随着计算机技术的发展, 计算能力、计算精度和存储空间不再成为算法发展及应用的瓶颈, 对数据的处理形式存在着更多的可能性。

文中在以上研究思路的基础上, 提出一种回溯算法结合数据时序重构融合滤波的初始对准方法, 该方法采用回溯的思路, 对在线数据进行存储再调用, 通过对数据的线下处理, 实现数据时序上的多样化重构, 构建多级滤波, 通过融合算法, 消除单一时序上的个性偏差, 从而实现有限对准时间内初始对准精度的进一步提高。

1 系统模型及滤波算法

一般初始对准过程为, 以主惯导注入参数作为观测量, 采用卡尔曼滤波对子惯导待修正状态量进行在线滤波估计。其中, 子惯导系统状态量通常选取11维参量, 包括北向、东向和天向失谐角误差, 北向和东向速度误差, 3个轴向的加速度计零偏以及3个轴向的陀螺漂移等, 即

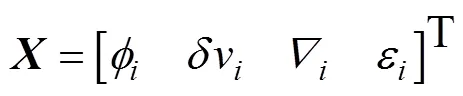
系统方程及观测方程分别为

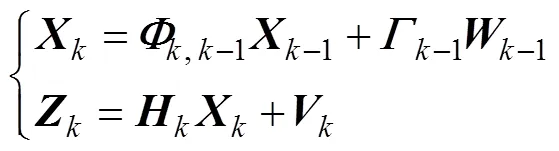
基于外界观测的修正量为主惯导注入参数与子惯导解析参数的差, 目前由于平台与子惯导之间的交互存在匹配上的限制, 一般采用速度匹配的方式, 可写作

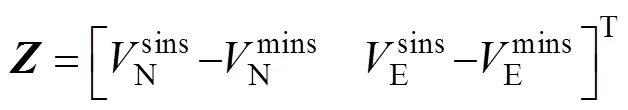
方程式中的具体系统误差矩阵及观测矩阵在此不作详细展开。卡尔曼滤波在线迭代过程为

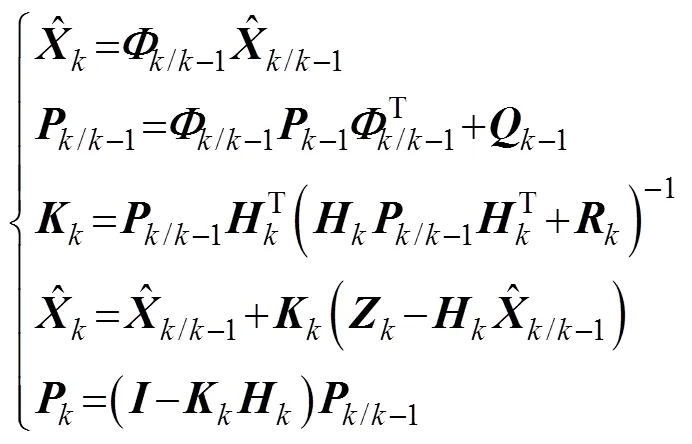
可以看出, 状态量的估计包含预测及修正两部分, 一步预测结果依靠系统建模, 修正偏差依靠外部注入观测量, 二者权值通过增益矩阵进行在线分配, 即

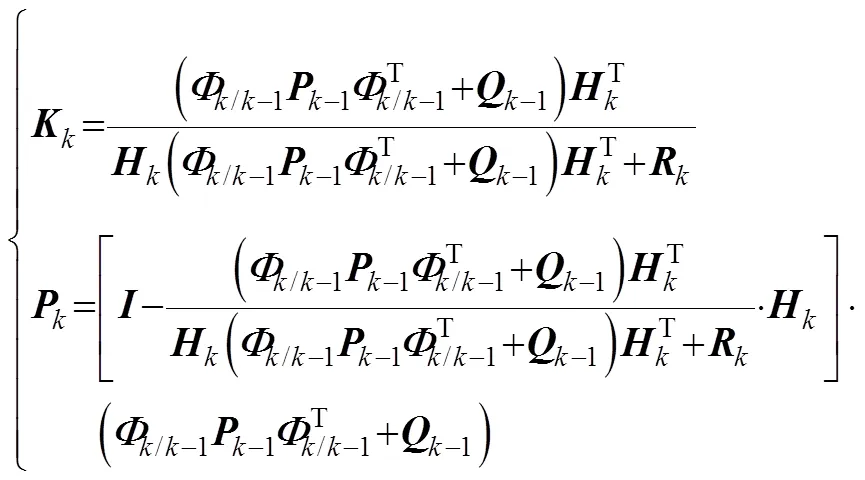
从式(5)可以看出, 当滤波器参数不变时,阵仅与系统误差阵相关。其中,阵可简化为

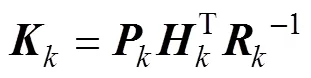
可以看出,阵及阵的迭代计算与外部观测量无关。随着迭代次数的增加,阵和阵依靠事先建立的滤波模型及参数进行程式化的收敛, 当收敛到一定程度时, 滤波预测程度与修正程度趋于平衡, 从而达到滤波稳态。即一次修正过程中, 滤波器收敛有效迭代步数受到阵、阵和阵初始化的限制[10-11]。

针对上述情况, 为延长滤波稳态到来的时间, 对状态量误差进行进一步估计, 可以在一定迭代步数后对的参数值进行重置, 或对阵和阵进行在线估计优化, 但这无疑增加了在线对准时间。回溯算法的应用在能够实现上述操作的同时, 达到兼顾缩短在线对准时间的目的。

2 回溯初始对准算法

回溯算法原理及流程如图1所示。

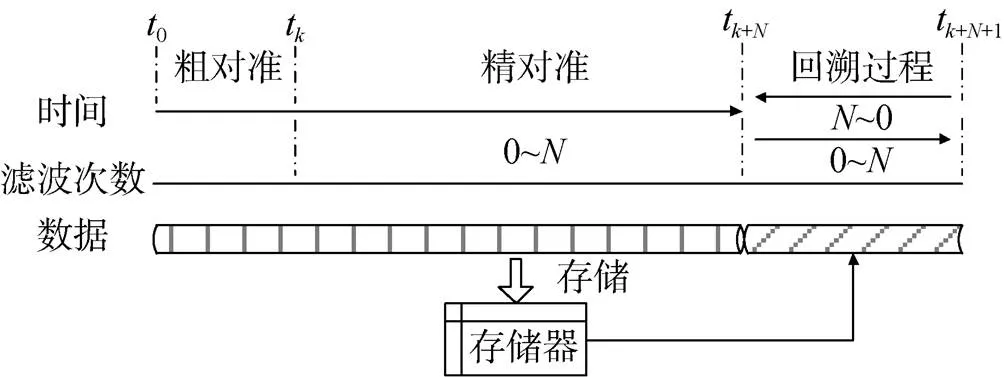
图1 回溯算法原理框图

一般初始对准分为粗对准和精对准过程以对初始误差进行修正, 在t时刻完成对准过程。回溯算法通过对在线数据进行存储, 在完成误差修正后, 再次调用存储数据, 同时对滤波器进行初始化, 以计算周期为时间单位再次进行“虚拟在线”滤波, 人为延长数据利用时间, 从而达到在几乎不占用对准时间条件下, 提高对准精度的目的[6-9]。

为保持数据时序上的连续性, 一般回溯算法采用“正向—逆向—正向”的滤波方式。下面采用一组实航数据对回溯算法的有效性进行仿真分析,该实航数据的姿态与惯性测量单元(inertial mea- surement unit, IMU)输出曲线如图2所示。

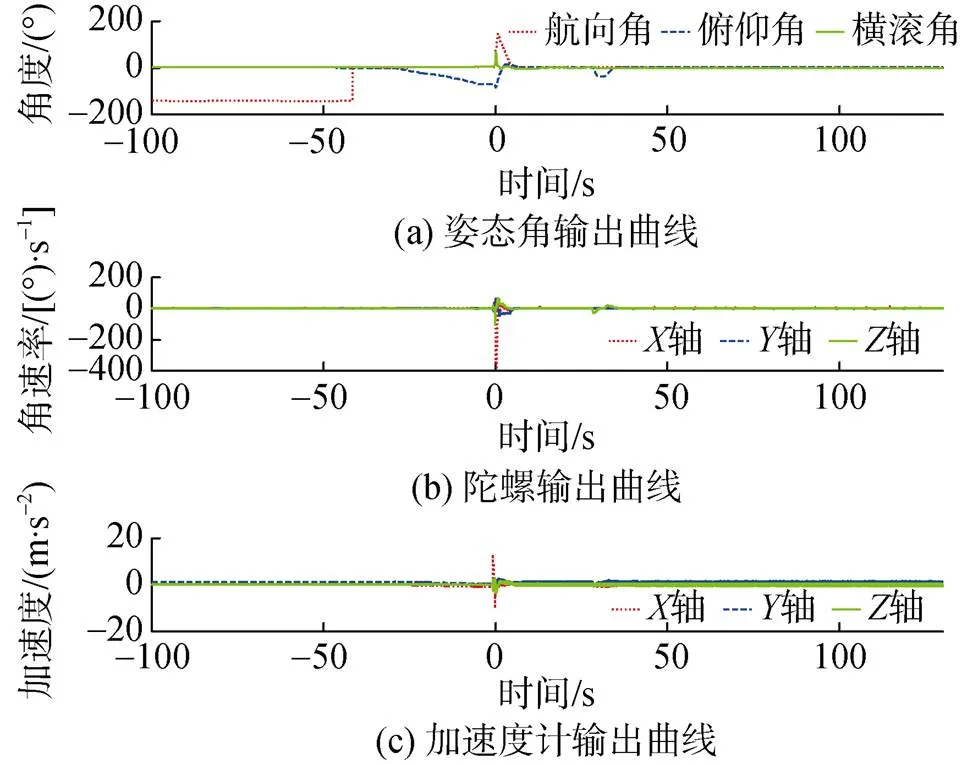
图2 实航数据姿态及IMU输出曲线

由图2可知, 按姿态变化可将实航过程分为射前和射后阶段, 在射前初始对准段分别进行常规及回溯初始对准, 其中回溯算法采用“正向—逆向—正向”的交替滤波时序。转导航后, 采集入水后的在线导航阶段解算的姿态及速度曲线进行比较, 对比结果如图3所示。

由图可知, 回溯算法能够有效减小姿态及速度初始误差, 在一定程度上也消除了由于姿态误差引起的水平速度累积误差。结果验证了回溯算法对改善对准精度及导航解算精度的有效性。

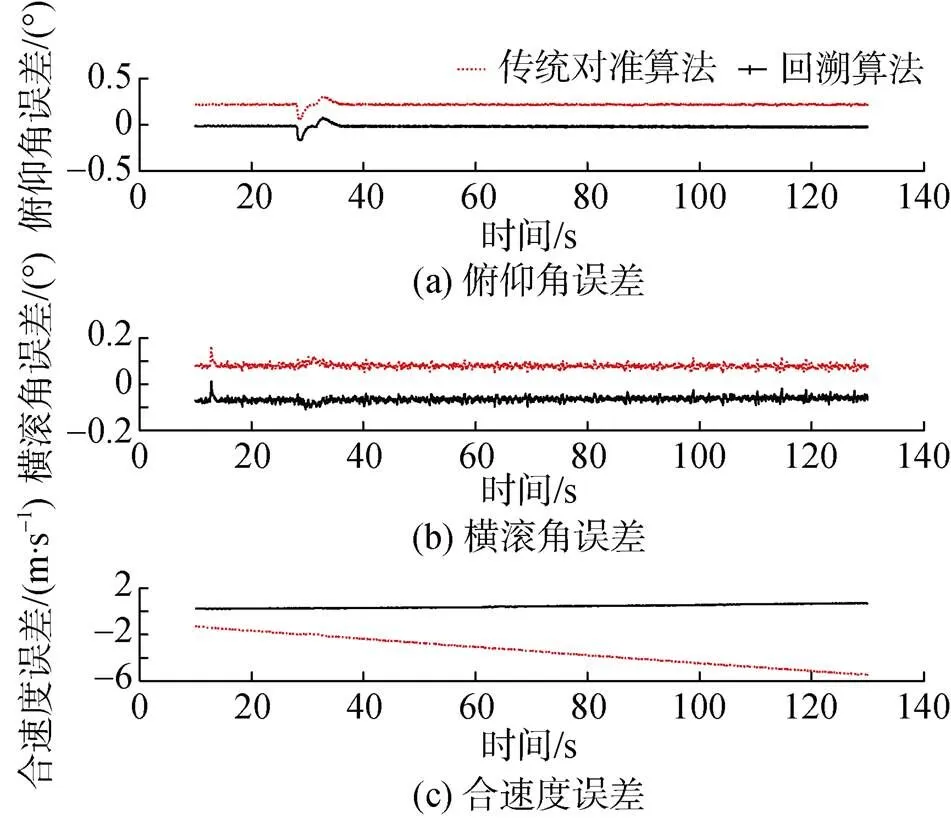
图3 传统对准算法与回溯算法修正后姿态及速度导航解算对比曲线

图4为北向和东向失谐角估计曲线。可以看出, 回溯算法的“正向—逆向—正向”滤波能够对失谐角误差进行进一步的估计, 但由于数据时序的不同, 其2次估计状态显示出了不同的估计效果。在此基础上, 开展存储数据时序上的多样性重构, 结合不同时序下的特性, 采用数据融合算法, 消除单向时序可能带来的个性偏差, 进一步提高初始对准精度。

3 回溯算法结合数据时序重构融合滤波算法

对存储数据时序多样性的重构, 可以打破“正向—逆向—正向”滤波的单一时序模式, 对存储数据加以充分利用及挖掘, 同时辅以具有良好稳健性、宽阔覆盖区域、高测量维数和强故障容错能力的多数据融合算法, 消除彼此差异可能带来的个性偏差, 进一步提高回溯算法的精度。

存储数据的重复调用及“虚拟在线”滤波过程, 及其基于数据整体时序的观测及处理模式, 为对数据进行时序重构、全局辨识、特征提取以及对滤波器进行适应性改进等操作提供了条件。

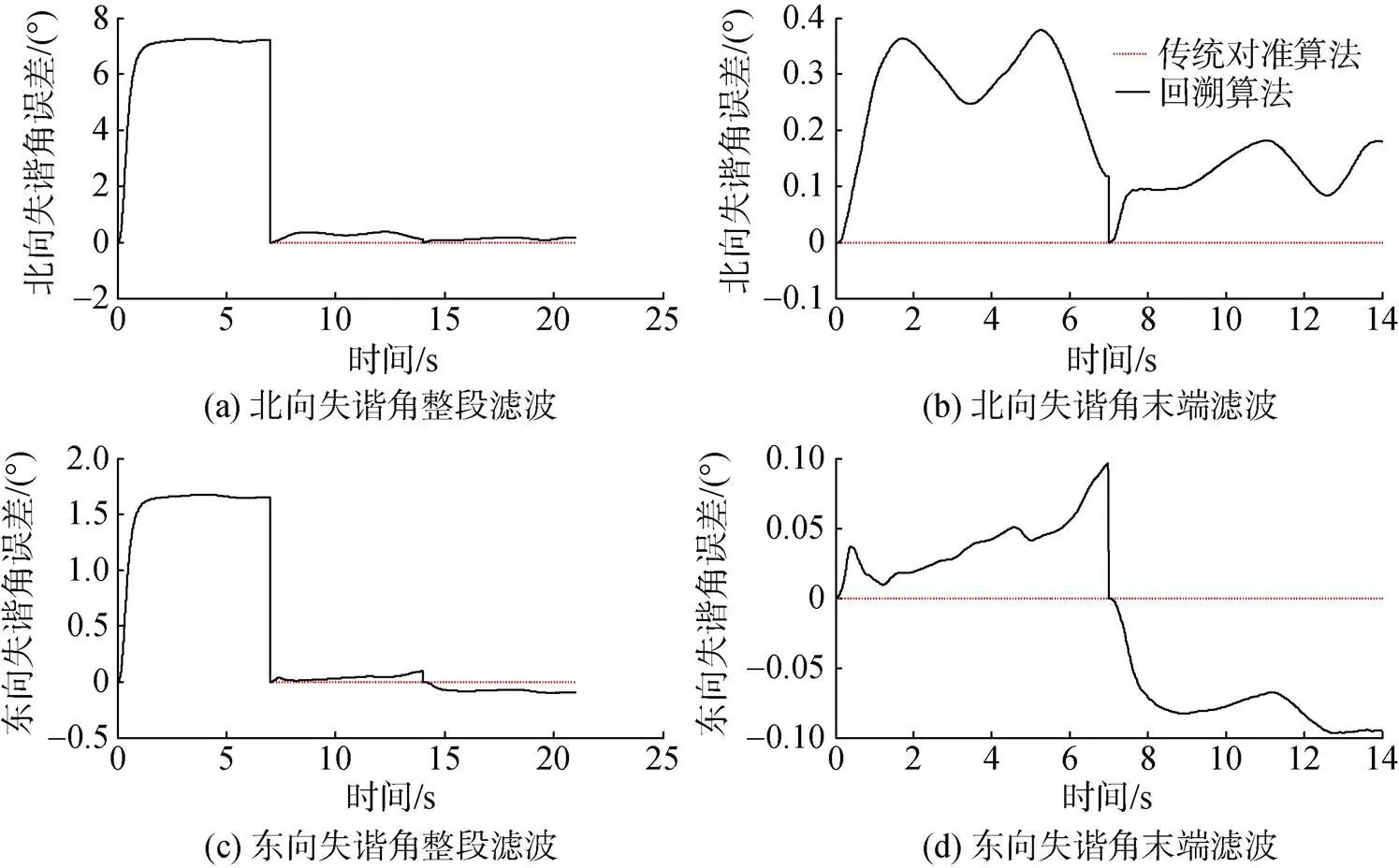
图4 传统对准算法与回溯算法失谐角估计对比曲线

对存储数据的重构首先必须具备一定的先决条件, 即重构后的数据在整体时序上需具备一定的连续性, 不能出现较大的时间跳动, 以免时序的跳跃带来数据上的断层, 从而导致滤波过程引入更大的初始误差。

设计某一条件下的回溯算法仿真试验, 其中俯仰角作正弦变化, 过程1为截取整数段周期的数据进行回溯, 过程2为截取整数段+0.25个周期的数据进行回溯。图5为2个过程的失谐角收敛状态曲线。

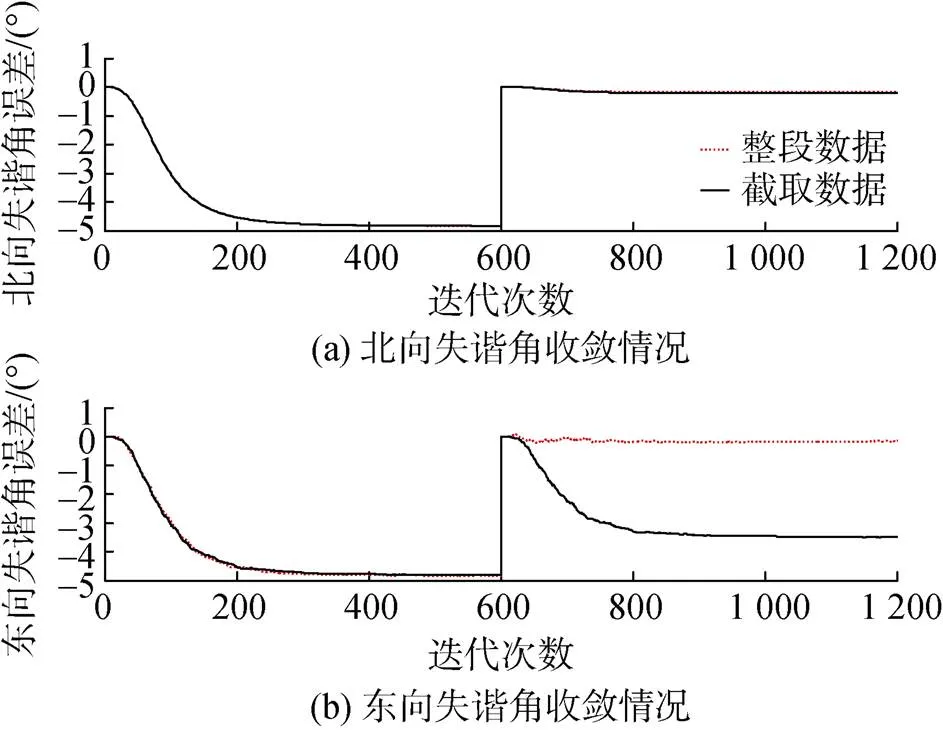
图5 整段数据与截取数据失谐角估计曲线

由图可知, 数据在滤波开始及结束节点的不对称性造成的二次滤波误差, 导致二次滤波需要对新增误差再次进行估计, 降低了二次滤波的效用。因此, 对存储数据进行重构前, 需根据对准工况、内部参数对数据进行整体辨识, 截取特定的数据段进行时序的重构及回溯。其中简单的方法是保证数据起始和终点2个时间点的匹配。

一般的载体平台在鱼雷进行初始对准时, 皆保持一定的稳定性, 不做较大主动机动, 此时, 在风浪和洋流的作用下形成的动基座可以简单地用三角函数叠加的形式进行描述, 即

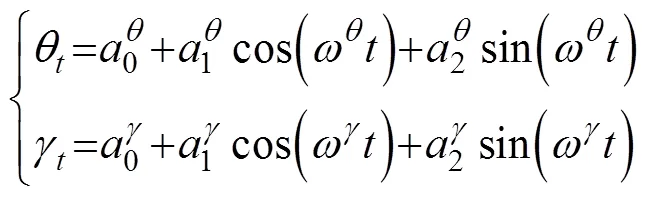
由于可以对数据进行整体处理, 加上一般载体平台晃动周期在15 s左右, 因此能够较为准确地对上述晃动公式进行辨识。利用数学仿真对采集的主惯导参数进行晃动特征三角函数的拟合, 在上述水平姿态函数的基础上, 将姿态的随机噪声设定为0.2°, 模拟晃动特征三角函数设定为

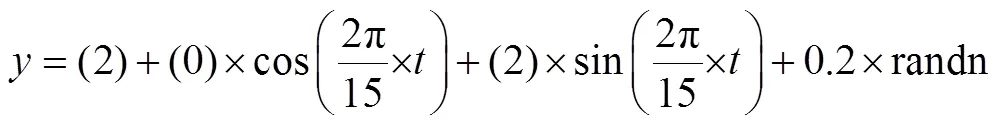
利用30 s的数据拟合得到的参数为

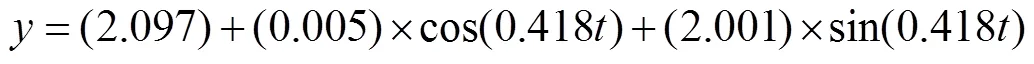
同时, 离线数据的处理可以实现在任何一点上提取到主惯导的注入参数、惯性测量组合输出参数以及导航解算得到的姿态、速度等信息, 因此, 可以避免在再次滤波开始时刻与修正时刻在数据上的不对称性。

文中选取4种存储数据重构方式: 正向、逆向、间隔正向+逆向以及间隔逆向+正向, 4种重构方式的操作公式如下

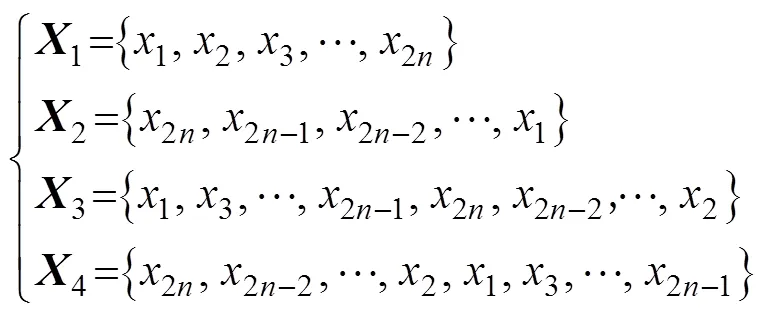
在上述不同重构模式下, 分别进行回溯算法初始对准仿真, 同时对4种滤波器估计结果通过下式进行融合

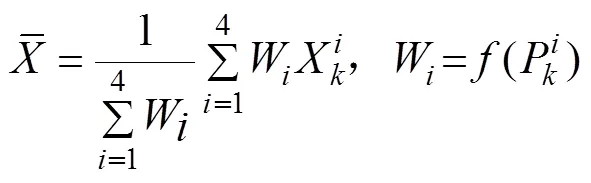
其中,为各重构方式的加权值, 其通过对各方式下的系统误差收敛情况进行权值分配。从而形成如图6所示的数据时序重构融合滤波算法。

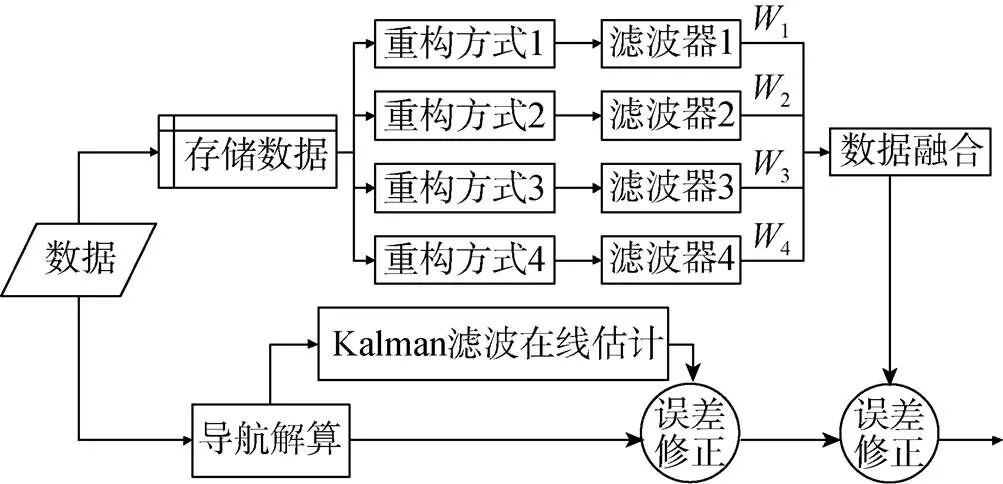
图6 数据时序重构融合滤波算法原理图

根据上图所示原理及流程, 对不同模式下的初始对准修正结果在实航数据条件下进行对比仿真, 如图7所示。

由上图可知, 由于数据时序上的重构, 不同方式显示出不同的初始残留误差, 实线为融合后的解算结果, 可以看出, 融合后的曲线结合了不同重构方式下的滤波特性, 中和了单一重构方式的个性偏差, 得到了较好的姿态及速度解算结果。

4 仿真试验与分析

文中提出的回溯算法结合数据时序重构融合滤波的初始对准方法(简称为“回溯重构算法”)在精度和时间上的有效性进行试验验证。采用常见的基于“正向—逆向—正向”滤波时序的回溯算法与文中方法进行对比, 二者失谐角估计收敛曲线如图8所示。

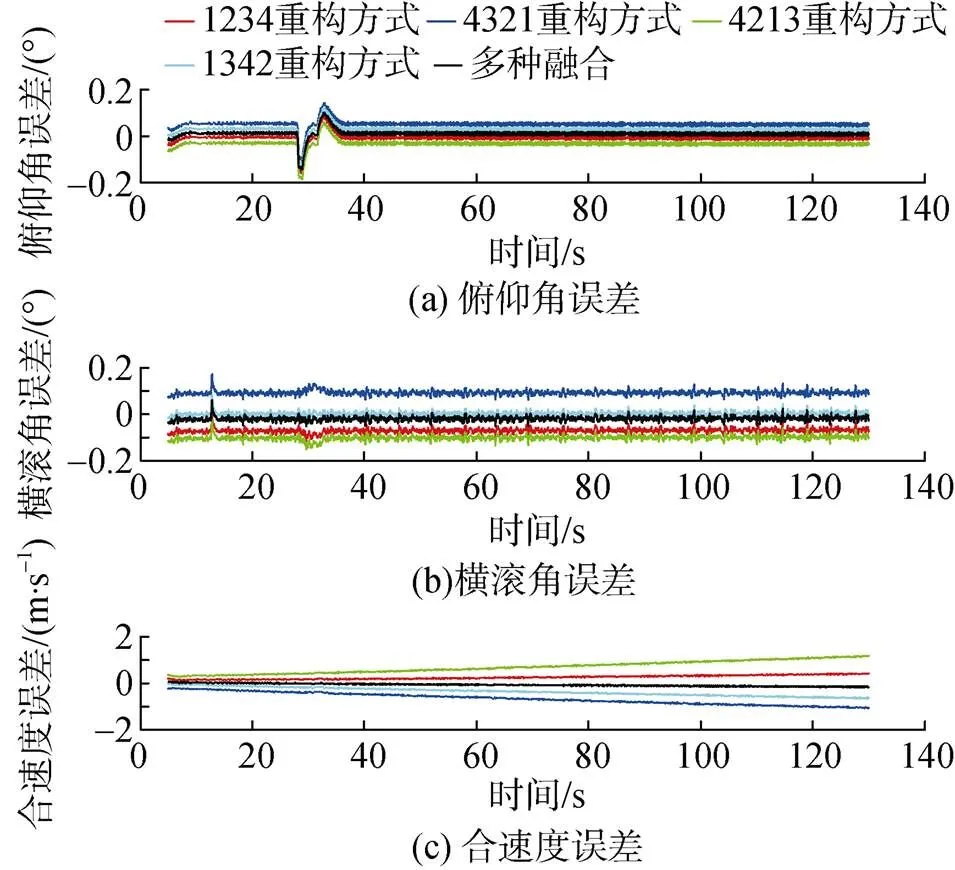
图7 不同重构方式及融合滤波的姿态与速度导航解算对比曲线

由图可知, 相比“正向—逆向—正向”滤波算法, 回溯重构方法在小角度误差下的二次收敛过程更加平稳可靠。

转导航后的在线导航阶段解算的姿态及速度曲线对比情况如图9所示, 其姿态及速度的初始误差及速度累积误差具体数值如表1所示。

通过表1数据可以看出, 相比基于“正向—逆向—正向”滤波时序的回溯算法, 回溯重构算法在经过姿态及速度初值补偿后, 姿态及速度初始误差明显减少, 且速度由于姿态初始误差造成的解算累积误差也相应更少。

以上从失谐角估计收敛曲线及修正后导航解算姿态及速度曲线两方面, 验证了文中所提出方法能够有效提高对准精度。

下面在相同的仿真验证试验条件下, 对初始对准过程中进行自适应调平, 通过滑动窗口实时对滤波收敛状态进行判定, 完成对准的自主调平,与完整时间的对准算法作比较, 验证文中所提算法在对准时间上的有效性。自适应调平后的失谐角估计收敛曲线如图10所示。

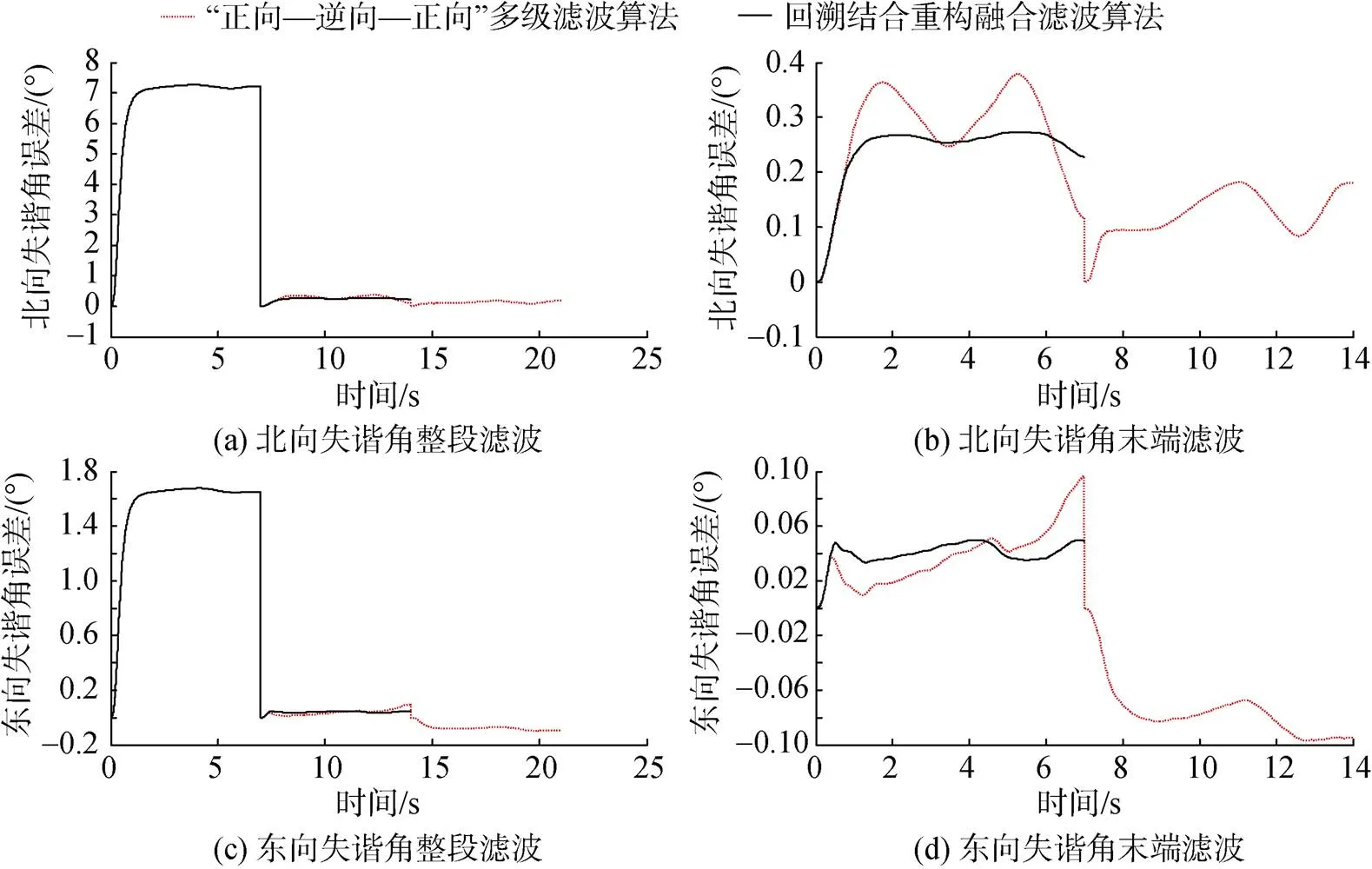
图8 回溯重构算法与回溯算法失谐角估计对比曲线

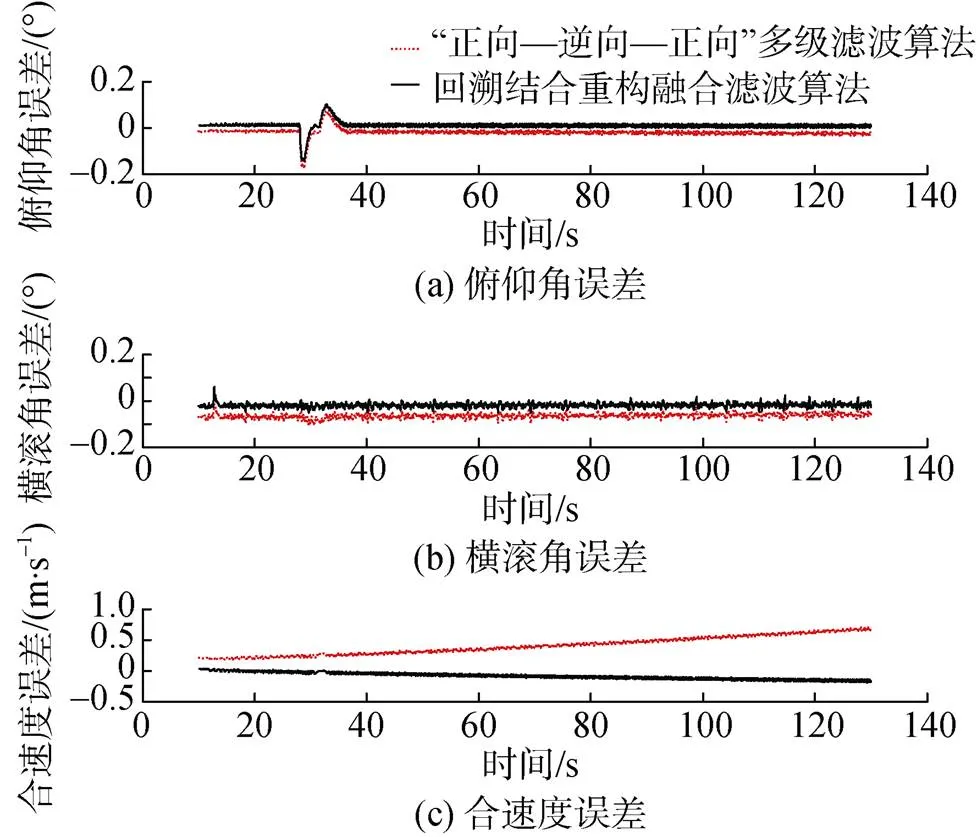
图9 回溯重构算法与回溯算法姿态与速度导航解算对比曲线

从图中可以看出, 一次自适应调平后虽然只占用了30.01 s的对准时间, 但通过数据存储调用及线下的多次滤波计算, 相比较完整时间下的对准算法, 仍能完整估计出失谐角误差(其中多级滤波中—线出现的阶梯状, 是由不同重构方式下的调平时刻不同而引起的)。

通过导航解算曲线进行修正精度验证结果如图11所示。

可以看出, 相比传统的对准算法, 自适应调平后虽然所利用数据量较少, 单次滤波时间较短, 但通过多次滤波能够达到相当的精度, 且由于结合了多种数据重构融合算法的使用, 在修正后, 其导航解算误差相比传统的回溯对准算法更小。

由此可以得出, 文中所提出算法, 不仅在一般回溯算法的基础上, 在相同数据量的条件下, 能够进一步的提高初始对准精度; 同时, 在较短的时间及较小的数据量条件下, 能够通过增加数据重构及融合滤波的次数, 达到与较多数据量相当的初始对准精度的目的。

表1 回溯重构算法与回溯算法初始误差

5 结束语

为兼顾鱼雷武器快速发射及精准制导的战术需求, 文中根据回溯算法工作原理, 利用存储数据整体处理模式的便利及优势, 提出一种回溯算法结合数据时序重构融合滤波的初始对准方法, 该方法在对数据进行整体辨识及特征段选取的基础上, 进行时序的多样性重构, 并行多次滤波后进行融合, 达到结合不同重构方式下的滤波特性,中和单一时序个性偏差的目的, 在有限时间内进一步提高初始对准精度。通过仿真试验, 验证了该方法相比传统对准算法和“正向—逆向—正向”滤波时序回溯算法在精度上的先进性, 以及在保证一定对准精度的前提下, 该算法在缩短对准时间上的有效性。

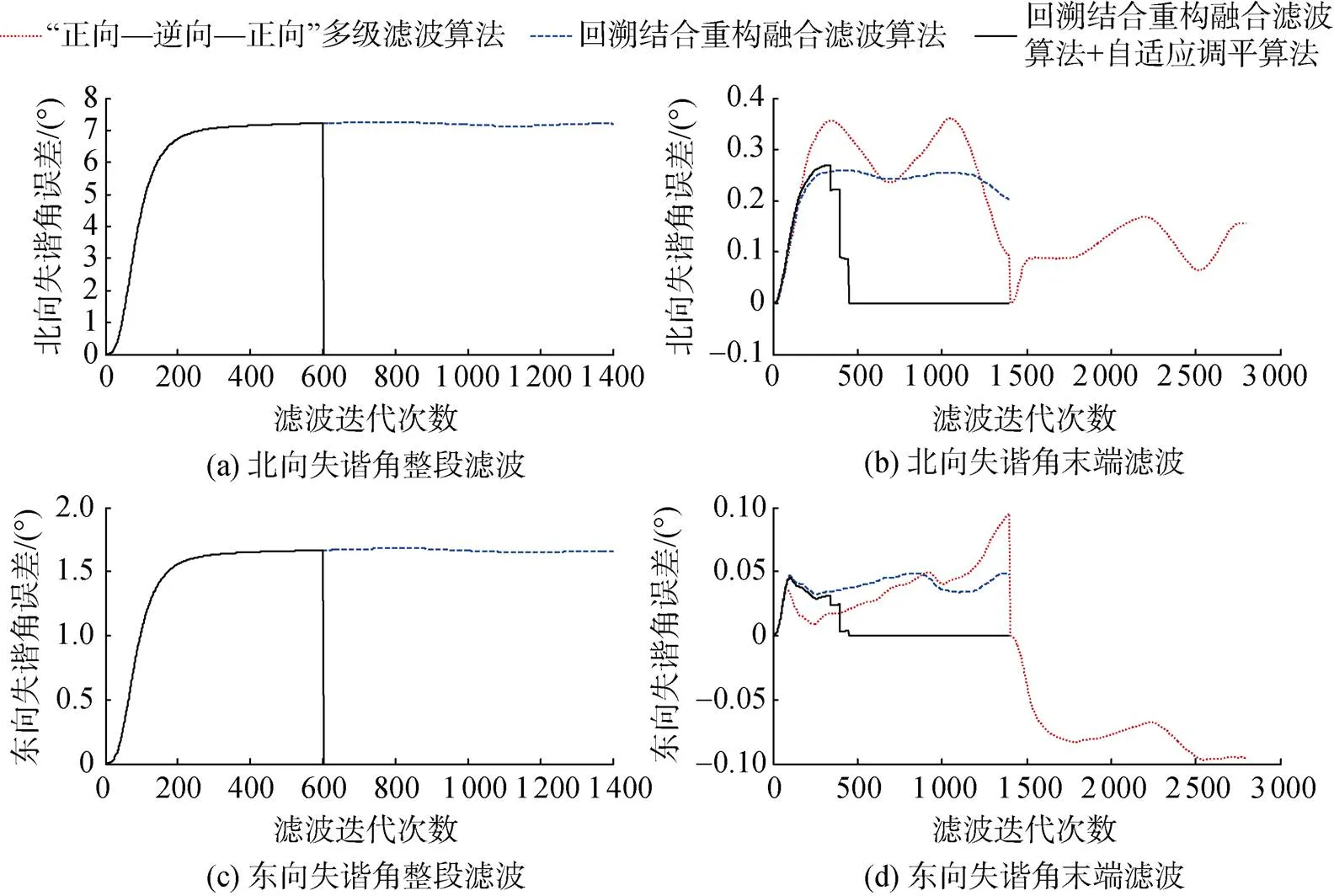
图10 自适应调平后失谐角估计曲线

表2 自适应调平后不同算法初始误差

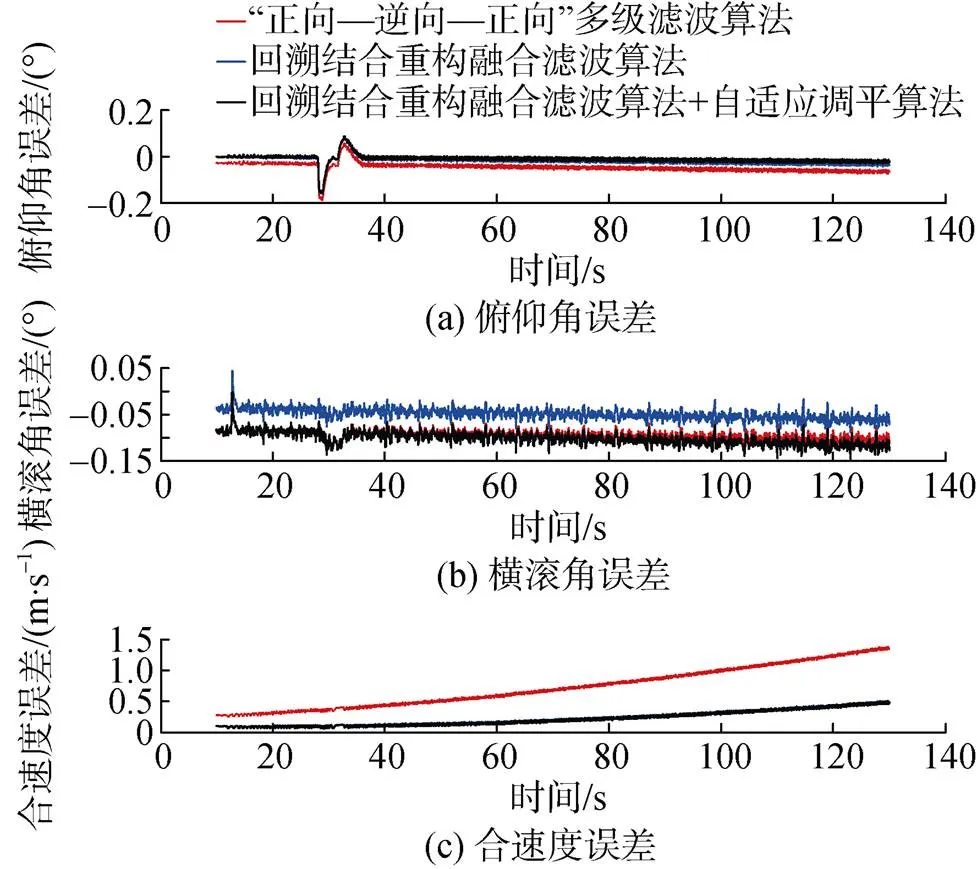
图11 自适应调平后姿态与速度导航解算对比曲线

[1] 高伟, 张鑫, 于飞, 等. 基于观测量扩充的捷联惯导快速初始对准方法[J]. 系统工程与电子技术, 2011, 33(11): 2492-2495.Gao Wei, Zhang Xin, Yu Fei, et al. Fast Alignment Method of SINS Using Measurement Augmentation[J]. Systems En- gineering and Electronics, 2011, 33(11): 2492- 2495.

[2] Acharya A, Sadhu S. Improved Self-Alignment Scheme for SINS Using Augmented Measurement[J]. Aerospace Science and Technology, 2011, 15(2): 125-128.

[3] 王岩, 王立文. 一种新的捷联惯导系统对准方法[J]. 鱼雷技术, 2010, 18(4): 282-286.Wang Yan, Wang Li-wen. A Transfer Alignment Method of SINS for Shipborne Torpedo[J]. Torpedo Technology, 2010, 18(4): 282-286.

[4] 张磊, 汪渤, 戴绍忠. 捷联惯导系统快速初始对准的多级组合滤波实现[J]. 系统仿真学报, 2008, 20(23): 6377-6379.Zhang Lei, Wang Bo, Dai Shao-zhong. Fast SINS Initial Alignment by Integrated Filtering Methods[J]. Journal of System Simulation, 2008, 20(23): 6377-6379.

[5] Wang S, Deng Z, Su L. Three-time Rapid Transfer Alignment Method of SINS/GPS Navigation System of High-Speed Marine Missile[J]. Journal of Harbin Institute of Technology(New Series), 2008, 15(2): 244-247.

[6] 李京书, 许江宁, 何泓洋, 等. 严格逆向过程的罗经回溯对准方法[J]. 系统工程与电子技术, 2014, 36(2): 348- 353.Li Jing-shu, Xu Jiang-ning, He Hong-yang, et al. Backtracking Scheme for Alignment with Strict Reverse Process Based on Compass[J]. Systems Engineering and Electronics, 2014, 36(2): 348-353.

[7] Thompson I C, Morgan K S. Rapid Self-Alignment of a Strapdown Inertial System Through Real-Time Reprocessing: US7739045[P]. 2006-5-31.

[8] 张朝飞, 罗建军, 侯永利. 抗扰动的捷联惯导系统回溯参数辨识对准法[J]. 中国惯性技术学报, 2015, 23(6): 734-738.Zhang Zhao-Fei, Luo Jian-Jun, Hou Yong-li. Anti-infe- rence Backtracking Parameter Identification Alignment Approach for Strapdown Inertial Navigation System[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 734-738.

[9] 刘锡祥, 徐晓苏, 李天旦, 等. 基于数据存储与循环解算的SINS快速对准方法[J]. 中国惯性技术学报, 2013, 21(6): 715-720.Liu Xi-Xiang, Xu Xiao-Su, Li Tian-dan, et al. Fast Alignment Method for SINS Based on Stored Data and Loop Calculation[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 715-720.

[10] Li J, Li Y, Jiang Q, et al. The Initial Alignment Method for Low-Cost Strapdown Inertial Navigation System Based on Kalman Filter[J]. Applied Mechanics and Materials, 2012, 220-223: 680-683.

[11] 王学斌, 徐建宏, 张章. 卡尔曼滤波器参数分析与应用方法研究[J]. 计算机应用与软件, 2012, 29(6): 212-215.Wang Xue-Bin, Xu Jian-Hong, Zhang Zhang. On Analysis and Application Approach for Kalman Filter Parameters[J]. Computer Applications and Software, 2012, 29(6): 212-215.

An Initial Alignment Method Using Backtracking Algorithm Combined with Data Sequence Reconstruction Fusion Filtering

YANG Guan-jin-zi1,2, LI Jian-chen1,2, GUO Lin-na1,2, HUANG Hai1

(1. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China; 2. Science and Technology on Underwater Information and Control Laboratory, Xi’an 710077, China)

In order to improve the initial alignment accuracy of torpedo and ensure shorter alignment time, on the basis of applying the backtracking algorithm to the initial alignment, a data sequence reconstruction fusion filtering method is proposed by calling and offline-processing the stored data. The proposed method can further improve the filtering estimation and alignment accuracy within a certain time compared with the traditional “forward-backward-forward” filtering backtracking algorithm by re-calling of the stored data, overall identification, feature extraction, time sequence reconstruction, and construction of a multi-stage filter. Comparison between simulation results and sea trial data proves the effectiveness of the proposed method in accuracy and time.

torpedo; initial alignment; backtracking algorithm; sequence reconstruction; fusion filtering

TJ630.33; U666.124

A

2096-3920(2020)03-0263-08

10.11993/j.issn.2096-3920.2020.03.004

2019-05-19;

2019-07-21.

杨管金子(1988-), 男, 在读博士, 工程师, 主要研究方向为鱼雷制导技术.

杨管金子, 李建辰, 国琳娜, 等. 一种回溯算法结合数据时序重构融合滤波的初始对准方法[J]. 水下无人系统学报, 2020, 28(3): 263-270.

(责任编辑: 陈 曦)