基于LMI的无人水下航行器干扰补偿控制

赵 旭, 龚时华, 杨 进

基于LMI的无人水下航行器干扰补偿控制

赵 旭, 龚时华, 杨 进

(中国船舶重工集团公司 第705研究所昆明分部, 云南 昆明, 650118)

针对无人水下航行器(UUV)航行时外界干扰复杂, 水动力导数计算不精确, 舵角受限以及存在非线性动态的问题, 提出了一种利用未知输入观测器对其未建模动态进行观测, 并依据李亚普诺夫函数设计干扰补偿控制律的方法, 同时考虑舵角饱和约束并将控制律设计过程转化为线性矩阵不等式最优化问题, 实现了对未知扰动的实时观测与补偿。将其应用到大型UUV航向航深控制上, 仿真结果表明, 该方法对未知输入具有很强的补偿能力, 提高了控制精度, 有效减少了控制律设计对水动力导数的依赖度, 改善了未知干扰作用下舵角的振荡特性。

无人水下航行器; 干扰; 线性矩阵不等式; 未知输入观测器; 饱和约束

0 引言

无人水下航行器(unmanned undersea vehicle, UUV)因具有自主航行能力, 可完成海洋/海底环境信息获取, 固定/移动目标探测、识别、定位与跟踪以及区域警戒等任务, 具有重要的民用、军用价值, 已成为世界各国海洋装备的重要研究方向[1]。大型UUV作为水下作战的“基地”或“母艇”, 具有为水下小型无人集群提供停靠补给、环境评估及平台发射等功能, 并可输送多种有效载荷, 而受到国内外学者的关注[2]。UUV工作环境复杂, 干扰建模精度不高, 同时其运动的水动力导数难以精确计算, 使得UUV的高精度控制较为困难。但随着UUV水下勘察、探测及搜索研究的不断深入, 以及大型UUV内部载荷正常工作的需求, 对UUV控制精度以及抗干扰能力提出了更高的要求。

近十年来, 故障诊断与干扰观测技术发展迅速, 其中基于观测器的故障诊断技术, 由于能够给出定量的干扰观测值, 在故障诊断与估计领域引起学者的关注, 并针对扩张状态观测器[3]、滑模观测器[4]、自适应观测器[5]、学习观测器[6]及未知输入观测器(unknown input observer, UIO)[7]等展开了研究。在此基础上, 将干扰观测与反馈控制相结合, 实现闭环控制律补偿外界扰动, 能使系统获得较强的抗干扰能力。如Ye等[8]依据李亚普诺夫函数设计了自适应的观测与反馈控制律, 并证明其鲁棒性, 但其需要干扰的先验知识; Seron等[9]则直接利用系统测量状态进行模型误差估计, 并由控制律实现干扰补偿, 但直接计算法干扰估计误差较大, 且要求输入矩阵可逆; Alwi等[10]则利用积分滑模观测器进行干扰观测, 并通过控制分配实现补偿, 但未考虑输入饱和约束对控制稳定性的影响。

为了解决以上问题, 文中利用UIO能够解耦不匹配扰动[11], 实现对匹配扰动的鲁棒最优干扰观测的特性, 依据李亚普诺夫函数推导了闭环系统干扰补偿反馈控制律, 同时为了降低舵机的饱和输出, 引入饱和约束, 将以上条件均转换为线性矩阵不等式(linear matrix inequality, LMI)求解, 从而实现对干扰的补偿, 并证明了其鲁棒性。整个设计流程较以往方法更易于实现, 不需要干扰先验条件, 有效降低了控制律设计过程中对水动力导数的需求, 提升了干扰作用下的控制精度。

1 UUV干扰补偿控制问题基本描述

含有UIO的系统, 是利用UIO观测外界扰动, 并在控制律中对其观测的扰动进行补偿。其基本结构如图1所示。

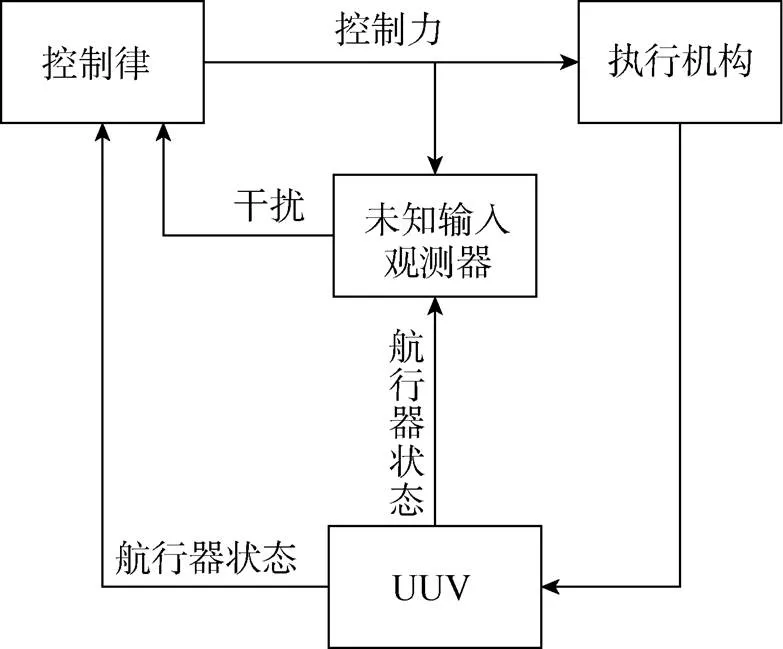
图1 UUV控制系统结构示意图

由于大型UUV一般处于低速、小俯仰角、小滚动角的运动状态, 可对其动力学进行线性化处理, 方便后续控制律推导, 而线性化过程中忽略的非线性以及耦合特性, 可通过UIO对其进行观测, 由控制律补偿。

基于UIO的UUV航向航深控制问题的关键在于如何设计UIO, 以保证对外界扰动的稳定观测, 以及如何设计控制律, 对扰动进行补偿, 并保证其闭环的鲁棒性能。

2 UIO设计

考虑到实际工程中采用数字信号进行控制, 引入线性离散模型

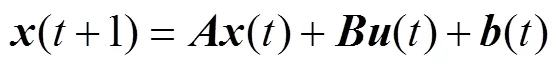
扰动按类型可分为匹配扰动与不匹配扰动, 匹配扰动与控制输入具有相同的输入矩阵[11], 令

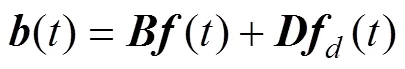
由模型可以看出, 匹配扰动可由控制输入直接进行补偿, 不匹配扰动直接补偿则较为困难。实际上, 匹配扰动包括水动力参数摄动、动力学耦合项、水动力高阶导数等, 不匹配扰动则包括运动学线性化误差、位置角度导航误差等。考虑将不匹配扰动交由控制律进行鲁棒抑制, 而匹配扰动通过UIO观测器进行观测, 并直接补偿。

由于UIO观测器特性可以完全解耦不匹配扰动对其观测过程的干扰。为了观测扰动, 建立增广系统模型如下

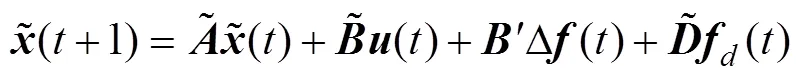
构造UIO对增广系统进行观测, UIO形式如下

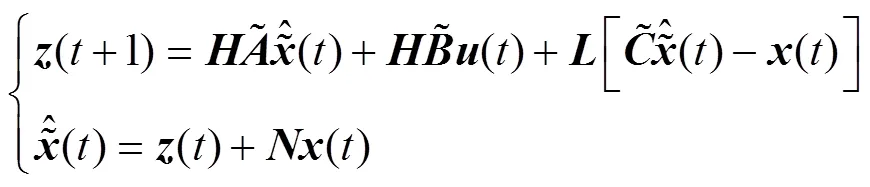
令

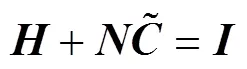
并在式(3)的等式右边乘上单位阵, 得

联立式(4)和式(6), 可得观测误差方程

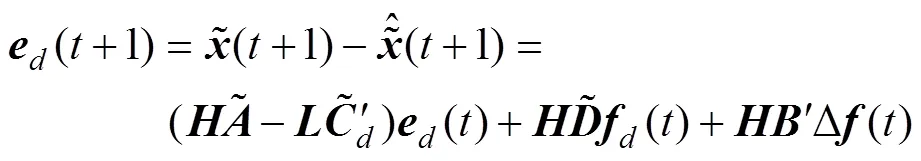
引理1:

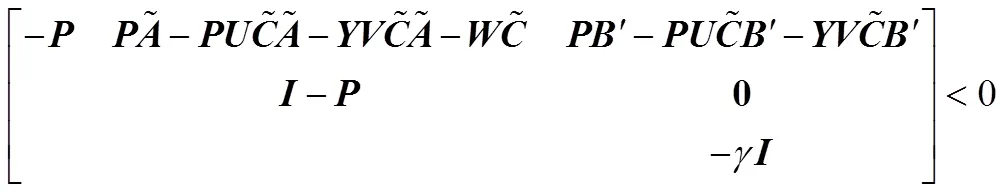
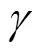
3 干扰补偿控制律

构造反馈控制律如下

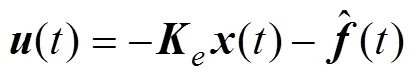
将式(10)代入到式(1), 得

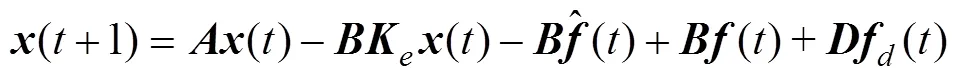
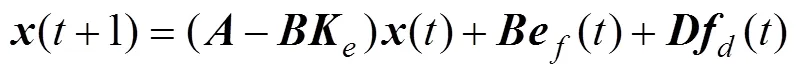
定理1:

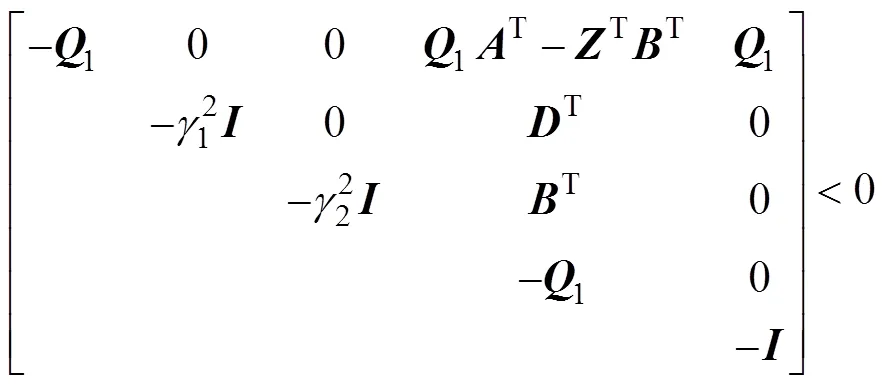
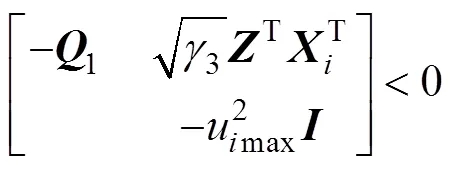
证明: 定义李亚普诺夫函数

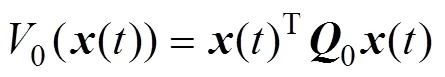
则有

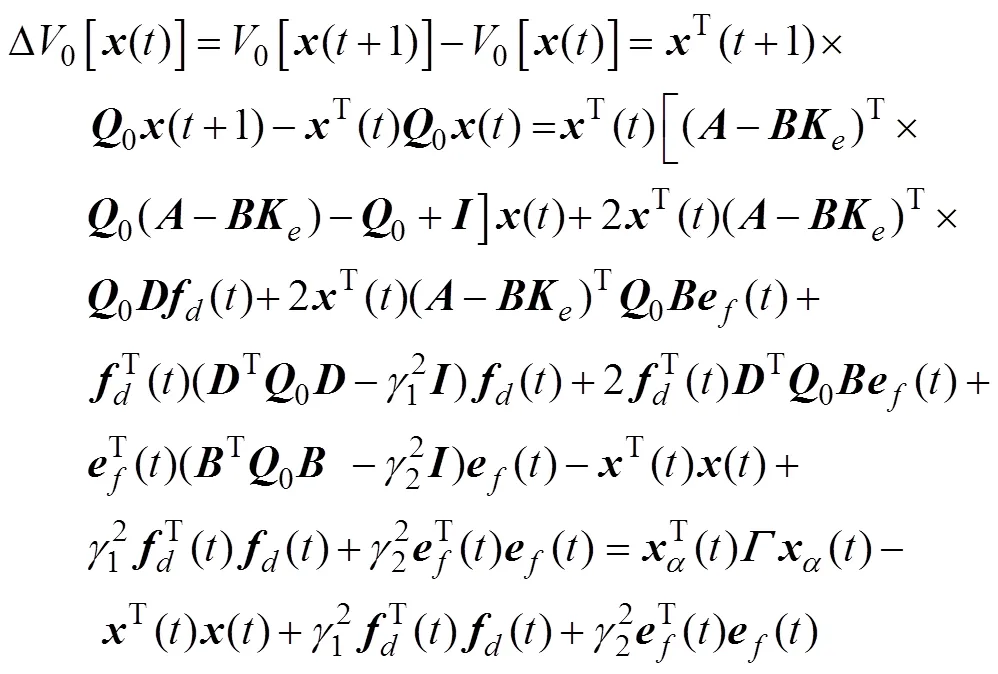
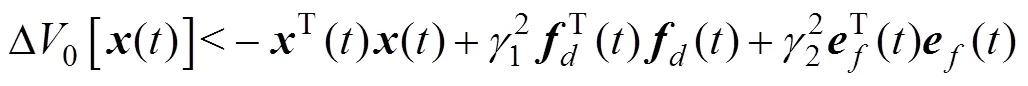
在零初始条件下

式(18)可写为

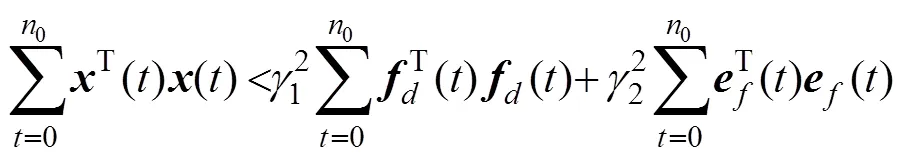
则有

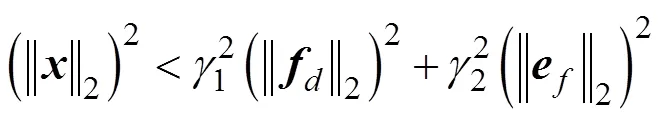
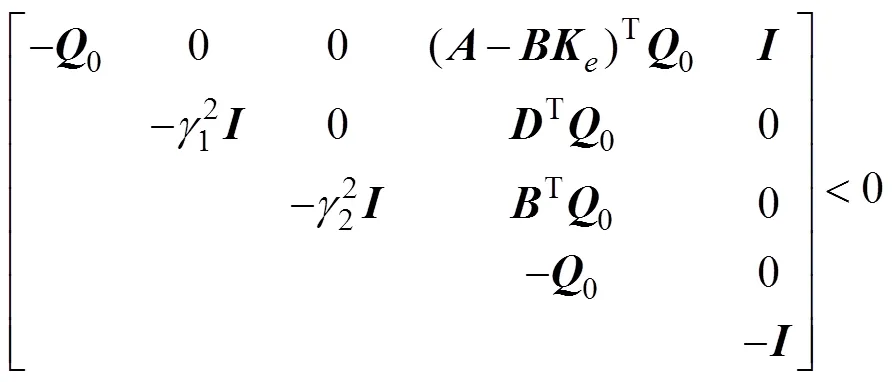
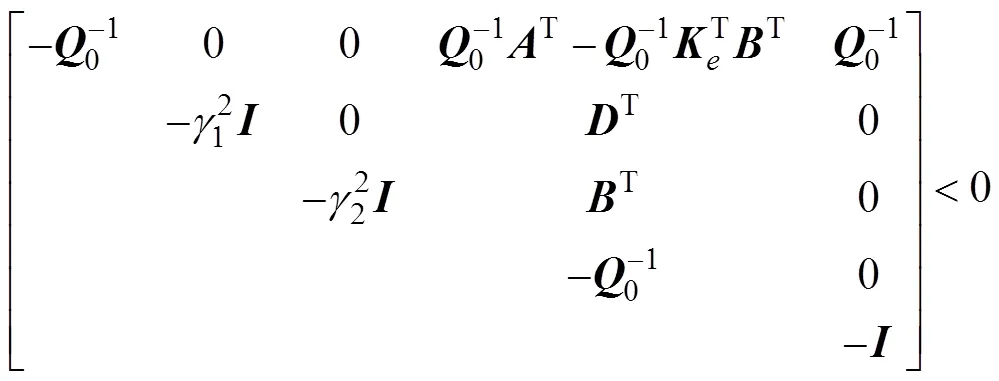
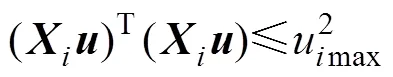
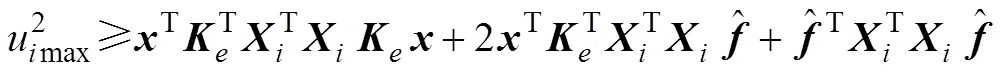
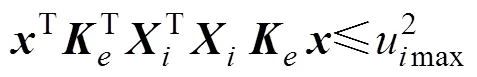
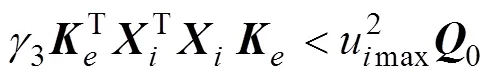
式(28)可写成

根据Schur补引理, 式(29)等价于

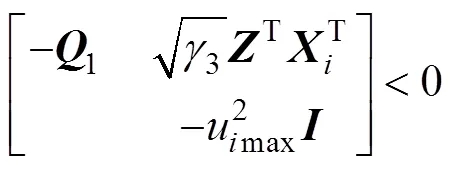
定理1得证。

4 仿真验证

4.1 UUV控制模型

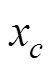
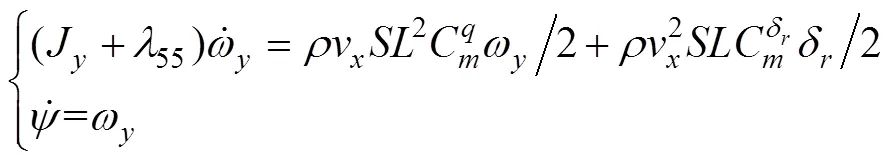
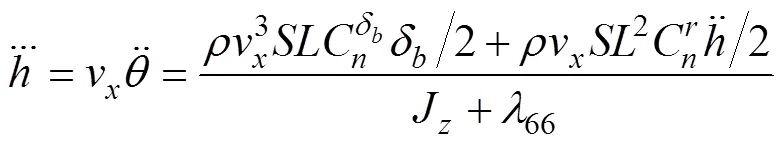
其简化的航深航向控制模型如下

整理式(32)和式(33), 得式(34)矩阵中变量

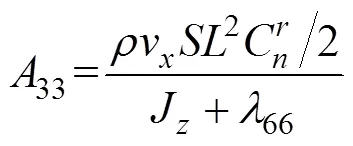
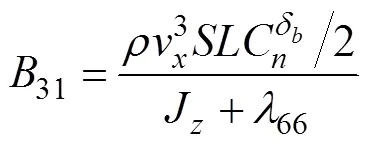
对式(32)进行离散化, 可得

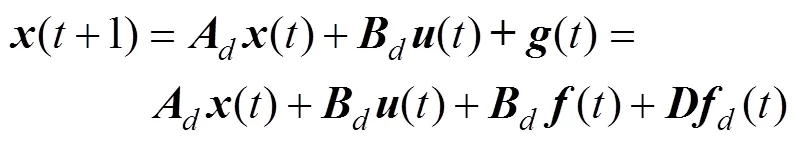
4.2 仿真结果与分析

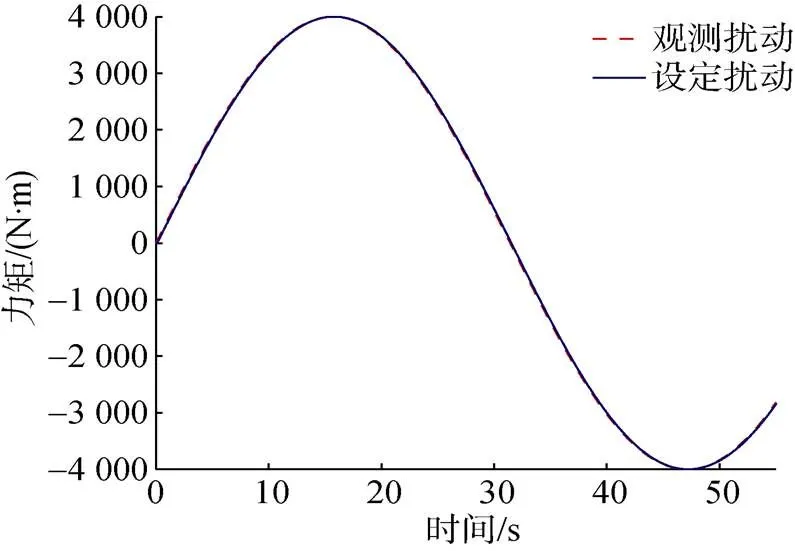
图2 扰动观测曲线

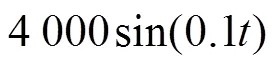
由于实际中, UUV的6个自由度互相耦合, 还存在其余未建模水动力导数, 同时运动学也并非严格线性, 这些扰动难以以一个解析的表达式描述, 为了验证该方法在大型UUV中处理如上未建模动态的控制性能, 同时验证线性化模型对设计控制律的有效性, 被控对象采用六自由度运动的UUV, 其动力学方程为

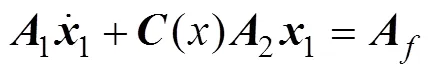
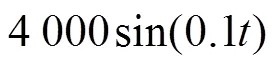
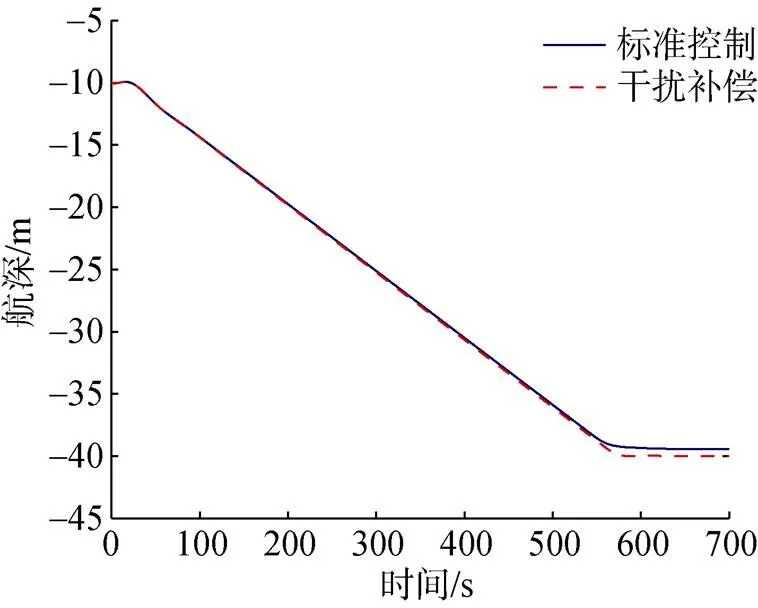
图3 航深控制曲线

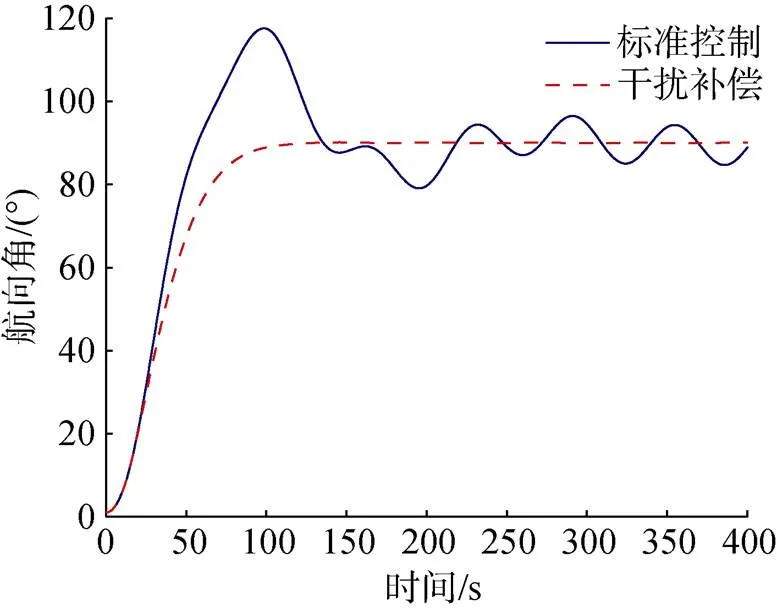
图4 航向角控制曲线

从图3和图4中可以得到如下结论:

1) 对于常值干扰, 干扰补偿有效降低了稳态误差, 稳态误差从0.5 m降低至0.1 m;

2) 对于周期性扰动, 干扰补偿能够有效补偿未知周期性扰动, 干扰作用下稳态误差仅有0.5°, 有效提升了控制精度;

3) 不进行干扰补偿时, 被控对象将因周期性外界扰动而呈现出明显的周期性特征;

4) 虽然线性模型于巡航速度2 m/s处建立, 但若速度出现偏差, 实际速度为1.6 m/s, 导致模型水动力导数出现摄动, 系统仍然可以稳定。

同时, 为说明抗饱和处理的有效性, 给出不抗饱和与抗饱和处理后的舵角输出见图5和图6。

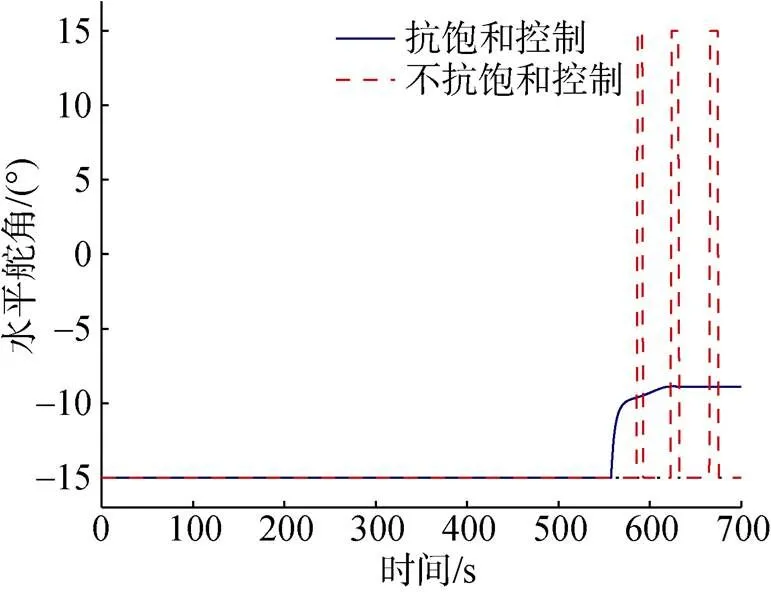
图5 抗饱和/不抗饱和时水平舵角输出对比曲线

图6 抗饱和/不抗饱和时垂直舵角输出对比曲线

从图5和图6中可以得出以下结论:

1) 抗饱和处理后, 被控对象受到周期性扰动的影响, 舵角也呈现出周期性特征, 用于对抗外界干扰;

3) 不抗饱和处理中, 舵角一直处于最大输出, 且在最大正负舵角中不停切换, 这种工作模式极易造成舵机损坏, 而抗饱和处理后改善了这一特性, 可有效保护舵机;

4) 不抗饱和处理时, 受舵角处于最大幅值振荡影响, 航向与航深也处于高幅振荡状态, 系统处于临界稳定, 并不符合控制需求。

5 结束语

针对UUV控制律设计依赖水动力导数, 外界未知干扰建模困难, 难以实现高精度控制的问题, 文中利用UIO观测扰动并结合鲁棒最优控制律对其进行补偿, 提高了在扰动作用下的控制精度, 同时在控制律设计中引入饱和特性, 改善了舵角输出, 避免了传统鲁棒控制的高增益反馈对舵机的损坏, 将以上约束设计为LMI最优问题, 方便计算。仿真结果表明, 该方法能够估计系统存在的外扰动, 有效抑制扰动对于控制精度的影响, 改善系统抗干扰能力。未来将进一步研究观测器在传感器噪声影响下如何进行匹配扰动解耦观测并进行控制补偿的方法。

[1] 潘光, 宋保维, 黄桥高, 等. 水下无人系统发展现状及其关键技术[J]. 水下无人系统学报, 2017, 25(1): 44-51.

Pan Guang, Song Bao-wei, Huang Qiao-gao, et al. Development and Key Techniques of Unmanned Undersea System[J]. Journal of Unmanned Undersea Systems, 2017, 25(1): 44-51.

[2] 钟宏伟, 李国良, 宋林桦, 等. 国外大型无人水下航行器发展综述[J]. 水下无人系统学报, 2018, 26(4): 273-282.

Zhong Hong-wei, Li Guo-liang, Song Lin-hua, et al. Development of Large Displacement Unmanned Undersea Vehicle in Foreign Countries: a Review[J]. Journal of Unmanned Undersea Systems, 2018, 26(4): 273-282.

[3] 廉成斌, 唐献平, 荆雪燕, 等. 鱼雷型无人水下航行器鲁棒控制器设计[J]. 舰船科学技术 2016, 38(7): 77-81.

Lian Cheng-bin, Tang Xian-ping, Jin Xue-yan, et al. Design Method of Robustness Controller for Torpedo Type Unmanned Underwater Vehicle[J]. Ship Science and Technology, 2016, 38(7): 77-81.

[4] 张爱华, 胡庆雷, 霍星, 等. 过驱动航天器飞轮故障重构与姿态容错控制[J]. 宇航学报, 2013, 34(3): 369-376.

Zhang Ai-hua, Hu Qing-lei, Huo Xing, et al. Fault Reconstruction and Fault Tolerant Attitude Control for Over- Activated Spacecraft under Reaction Wheel Failure[J]. Journal of Astronautics, 2013, 34(3): 369-376.

[5] Shen Y, Liu L, Dowell E H. Adaptive Fault Tolerant Robust Control for a Linear System with Adaptive Fault Identification[J]. IET Control Theory & Applications, 2013, 7(2): 246-252.

[6] Jia Q H, Chen W, Zhang Y C, el al. Robust Fault Reconstruction Via Learning Observers in Linear Parameter-varying Systems Subject to Loss of Actuator Effectiveness[J]. IET Control Theory & Applications, 2014, 8(1): 42-50.

[7] Gao Z, Liu X, Chen M Z Q. Unknown Input Observer-Based Robust Fault Estimation for System Corrupted by Partially Decoupled Disturbance[J]. IEEE Trans. Industrial Electronics, 2016, 63(4): 2537-2547.

[8] Ye D, Park J H, Fan Q. Adaptive Robust Actuator Fault Compensation for Linear Systems Using a Novel Fault Estimation Mechanism[J]. International Journal of Robust & Nonlinear Control, 2016, 26(8): 1597-1614.

[9] Seron M M, De Doná J A. Robust Actuator Fault Compensation Accounting for Uncertainty in the Fault Estimation[J]. International Journal of Adaptive Control & Signal Processing, 2014, 28(12): 1440-1453.

[10] Alwi H, Edwards C. Fault Tolerant Control Using Sliding Modes with On-line Control Allocation[J]. Automatica, 2008, 44(7): 1859-1866.

[11] Hashemi M, Kamali E A, Naraghi M. Fast Adaptive Fault Estimation for Linear System with Actuator Effectiveness Loss and Unmatched Unknown Inputs[C]//2016 4th International Conference on Robotics and Mechatronics (ICROM). Tehran, Iran: IEEE, 2016: 278-284.

[12] Zhou M, Shen Y, Wang Q. Robust UIO-based Fault Estimation for Sampled-data Systems: an LMI Approach[C]//2013 IEEE International Conference on Information and Automation (ICIA). Yinchuan, China: IEEE, 2013: 1308-1313.

[13] 严卫生. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2005.

Disturbance Compensation Control for Unmanned Undersea Vehicle Based on LMI

ZHAO Xu, GONG Shi-hua, YANG Jin

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

As regards the problems that an unmanned undersea vehicle(UUV) is subjected to complex external disturbance, the calculation of hydrodynamic derivative is inaccurate, the rudder angle is restricted, and nonlinear dynamic exists, a disturbance compensation control law is designed based on the Lyapunov function and the unknown input observer(UIO) to observe the unmodeled dynamics. After considering the rudder angle saturation constraint and transforming the control law design process into the optimization problem of linear matrix inequality, real-time observation and compensation of unknown disturbance are realized. Simulation results show that the proposed method has the ability to compensate disturbance and improve control precision, which facilitates the course and depth control of UUV, effectively reduces the dependence of the control law design on the hydrodynamic derivative, and improves the oscillation characteristics of rudder angle under unknown disturbance.

unmanned undersea vehicle(UUV); disturbance; linear matrix inequality(LMI); unknown input observer(UIO); saturation constraint

TJ630.33; TP13

A

2096-3920(2020)03-0271-07

10.11993/j.issn.2096-3920.2020.03.005

2019-03-01;

2019-05-31.

赵 旭(1992-), 男, 硕士, 主要从事水下航行器控制与故障诊断技术研究.

赵旭, 龚时华, 杨进. 基于LMI的无人水下航行器干扰补偿控制[J]. 水下无人系统学报, 2020, 28(3): 271-277.

(责任编辑: 杨力军)