几类根式函数的不定积分

赵继红

(宝鸡文理学院 数学与信息科学学院， 陕西 宝鸡 721013)

众所周知，有理函数的原函数是初等函数。但一般而言, 根式函数(或称无理函数)的原函数不一定是初等函数[1，2]。因此不同于有理函数不定积分的求解, 求根式函数的不定积分一般来说要更困难, 没有固定的公式和方法来套用, 需要根据题型灵活运用换元积分法和分部积分法。基于此事实, 本文中笔者整理了几类求解具有特殊形式的根式函数不定积分的有效方法, 通过选取适当的变量代换化解被积函数中由于根式的出现所带来的困难。需要指出的是, 一些根式函数不定积分的求解方法已在一些教材[1-3]和文献[3-6]中都提到, 但基本上都是贯穿于讲解不定积分的换元积分法时的举例, 例子分布离散, 方法总结不够全面, 本文的目的是将这些求解方法进行归纳整理, 总结出一般求解根式函数不定积分的技巧和方法, 便于学生学习, 加深对不定积分换元积分法的理解和掌握。贯穿全文, 我们用符号R(u,v,∧)来表示函数R是变量u,v,∧的有理函数。

1 最小公倍数法

解 令x=t[2,3]=t6,则原式可化为简单的有理函数的不定积分：

2 整体代换法

3 三角变换法

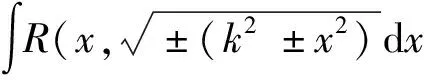
借助于辅助三角形即得

4 分部积分法

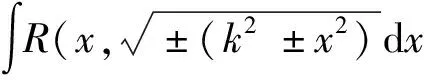
解 利用分部积分法, 得：

移项即得:

5 倒代换

当x>0时, 有t>0, 从而

同样, 当x<0时, 有t<0, 则

6 欧拉(Euler)变换法

ax2+bx+c=a(x-x1)(x-x2)

进一步, 通过恒等变形得

此类型的不定积分前文已经讨论过, 可以用整体代换法来求解。

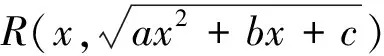
然后通过两边各自平方后消去x2项, 将原积分化为有理函数的不定积分。上述变换称为欧拉(Euler)变换。

将上述结果代入, 可将所求不定积分化为如下有理函数的不定积分：

综上, 在求解根式函数的不定积分时, 选取恰当的变量代换很关键, 而熟练地掌握和运用换元方法是基础。初学者一定要熟记求解不同类型的根式函数不定积分时所采用的方法和技巧, 解题才能对症下药, 并且不能拘泥于使用一种变量代换, 有时候需要同时进行好几次换元过程才能解决一些更复杂根式函数的不定积分。对于初学者而言, 一定要多做练习, 归纳题型, 总结方法, 深刻理解和掌握根式函数不定积分的各种换元方法以及灵活运用这些方法, 丰富和提高对微积分学理解层次的深度和厚度, 为后续内容的学习奠定一个良好的理论基础。