基于减基概念的凸集结构可靠性分析方法

张 正，吴曼颖，毕仁贵

(1.吉首大学 土木工程与建筑学院，张家界 427000；2.怀化学院 机械与光电物理学院，怀化 418008；3.吉首大学 物理与机电工程学院，吉首 416000)

1 引 言

准确而又高效地求解结构可靠性是机械设计、制造以及维护等领域不容忽视的一个重要工程分析问题[1,2]。结构可靠性分析中，较为常见的方法有改进的一次二阶矩法和蒙特卡洛法MCM[3,4]。在工程实践中，改进的一次二阶矩法通过构建验算点上的线性函数面去逼近极限状态曲面来模拟结构的可靠概率，所得到的可靠度较为粗糙保守且难具精准性，在应用上具有较大的工程局限性；MCM通过模拟随机变量进行计算，在不需考虑极限状态曲面性态的条件下可以准确地获得结构的可靠度，具有较佳的工程适宜性，该方法虽然具有较高的计算适应性，但是由于需要抽样大量的数据进行多次重分析，其计算效率直接与抽样数量和一次重分析的时间有关，故而最终的计算过程较为耗时。当工程结构可靠性分析涉及到大规模的有限元计算时，MCM模拟需要反复解算大量级的有限元问题，有限元的求解过程将使其可靠性分析流程极为耗时，甚至会使之丧失工程可行性。因此，针对大规模工程结构可靠性分析问题，如何使MCM模拟呈现出高效率的计算状态有重要意义。

减基法RBM[5-8]是一种能快速逼近工程问题解的概念性方法，文献[9]基于此开发了一种快速分析区间参数域结构可靠性的减基方法，发现引入减基法的MCM模拟具有较高的工程应用价值。然而在工程实践中，可靠性分析所遇到的问题不仅限于区间参数域结构情形，往往还会出现椭球凸集之类的复杂参数域结构问题[10-13]。椭球凸集参数域(以下简称椭球域)具有异于区间参数域的几何形态和特征性态，相较于区间参数域，其既不便于结构减基空间及减基列式的建构，也不便于MCM的减基抽样和模拟，新的问题需要新的解决方式。

鉴于此，针对椭球域结构的可靠性分析问题，提出了一种基于减基概念的高效解算方法。综合坐标系的正交变换及其逆向变换，在结构的椭球域上建立合适的减基空间和减基算法，同时在结构的椭球域上构建均匀的等概率参数抽样点集，之后在低维的减基空间中快速运行MCM模拟，从而实现了对结构可靠性的高效率分析。算例验证了该方法的工程可行性，并验证了其较之有限元分析具有较高的计算时效性。

2 可靠性问题描述

将椭球域结构的极限状态函数表达为

(1)

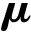
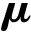
(2)

(3)

3 可靠性减基分析

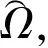
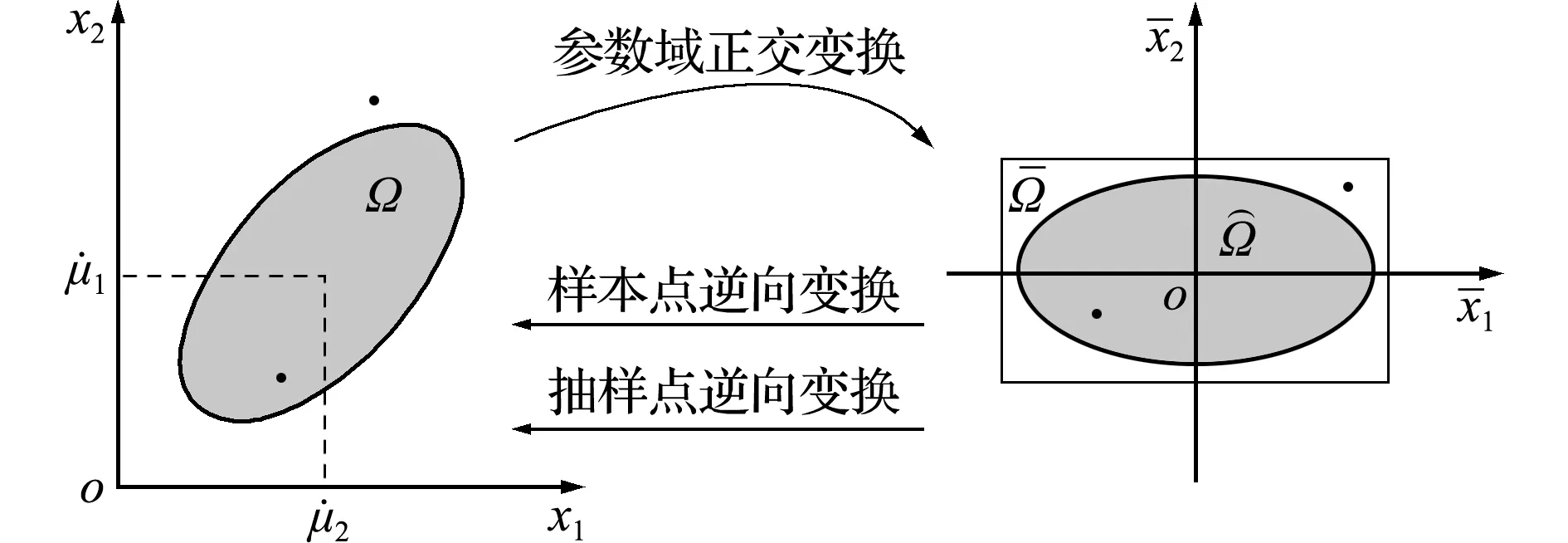
图1 椭球域下结构可靠性减基分析

Fig.1 Structural reliability reduction analysis on ellipsoid domain

3.1 椭球域下的减基列式

3.1.1 参数域正交变换

对于椭球域结构可靠性问题(3)所定义的椭球域Ω,分析其特征矩阵W，将W进行正交坐标变换，即进行如下的Schur变换[14]，

W=TTΛΤ

(4)

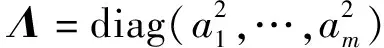
3.1.2 样本点逆向变换

将特征矩阵W的分解式(4)代入结构可靠性问题(3)所定义的椭球域Ω,得

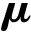
(5)

或记为

(6)

(7)

也可写为

(8)

3.1.3 减基列式的构建

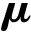
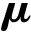
(9)

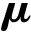
(10)

以及

3.2 椭球域下的减基模拟

3.2.1 抽样点逆向变换

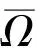
(12)

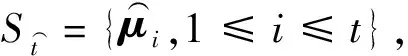
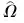
St={μi,1≤i≤t}

(13)

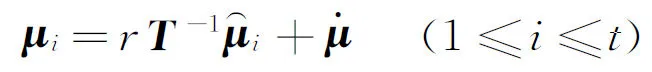
(14)

3.2.2 MCM减基模拟

对于椭球域结构可靠性问题(3)，利用减基法进行快速逼近，并依据减基列式(10，11)可以将其变为减基形式下的极限状态函数式

(15)

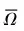
(17)

4 可靠性计算流程

针对椭球域结构的可靠性问题，本文提出的可靠性分析方法可分为离线处理和在线计算两个阶段。离线处理阶段，主要是构建椭球域下的减基列式和椭球域中的均匀抽样点集，并予以保存；在线计算阶段，主要是实施MCM减基快速模拟，并获得结构的可靠度逼近值及其数值可靠域，其计算流程如图2所示。其中，在线计算模块MCM的减基模拟的具体计算步骤如下。

图2 椭球域结构的可靠性计算流程

Fig.2 Computational process of reliability for the ellipsoidal structure

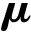
5 数值算例测试

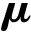
(18)

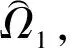
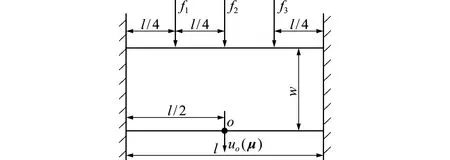
图3 结构数值算例

Fig.3 Numerical example of structure

图4 测试算例的两种椭球域情况

Fig.4 Two ellipsoidal domains for the testing example

图5 关于椭球域Ω1的减基空间样本点分布

Fig.5 Distribution of sample points for the ellipsoid domainΩ1

图6 椭球域Ω1中MCM减基模拟的数值可靠域

Fig.6 Numerical reliability domain by MCM reduced-basis simulation on the ellipsoid domainΩ1

在同一台计算机上，对于椭球域Ω1情况，利用MCM减基模拟执行的可靠性分析，消耗的在线平均计算时间约为166 s；如果在MCM减基模拟同时加入稀疏矩阵技术，则消耗的在线平均计算时间可进一步降为约59 s；而利用MCM有限元模拟并配合相应的稀疏矩阵技术所实施的可靠性分析，耗费的平均计算时间约为1495 s。显见，在椭球域结构的可靠性分析中，MCM减基模拟方法相较于MCM有限元模拟方法具有较高的计算时效性，而这种相对的高时效性主要是由MCM的大批量和RBM的低维性所造成的。

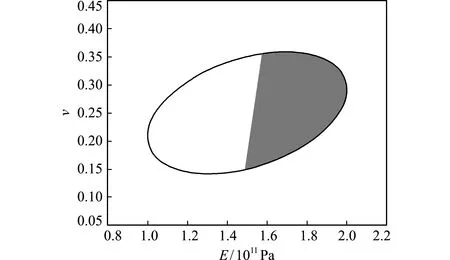
图7 椭球域Ω1中MCM有限元模拟的数值可靠域

Fig.7 Numerical reliability domain by MCM finite-element simulation on the ellipsoid domainΩ1

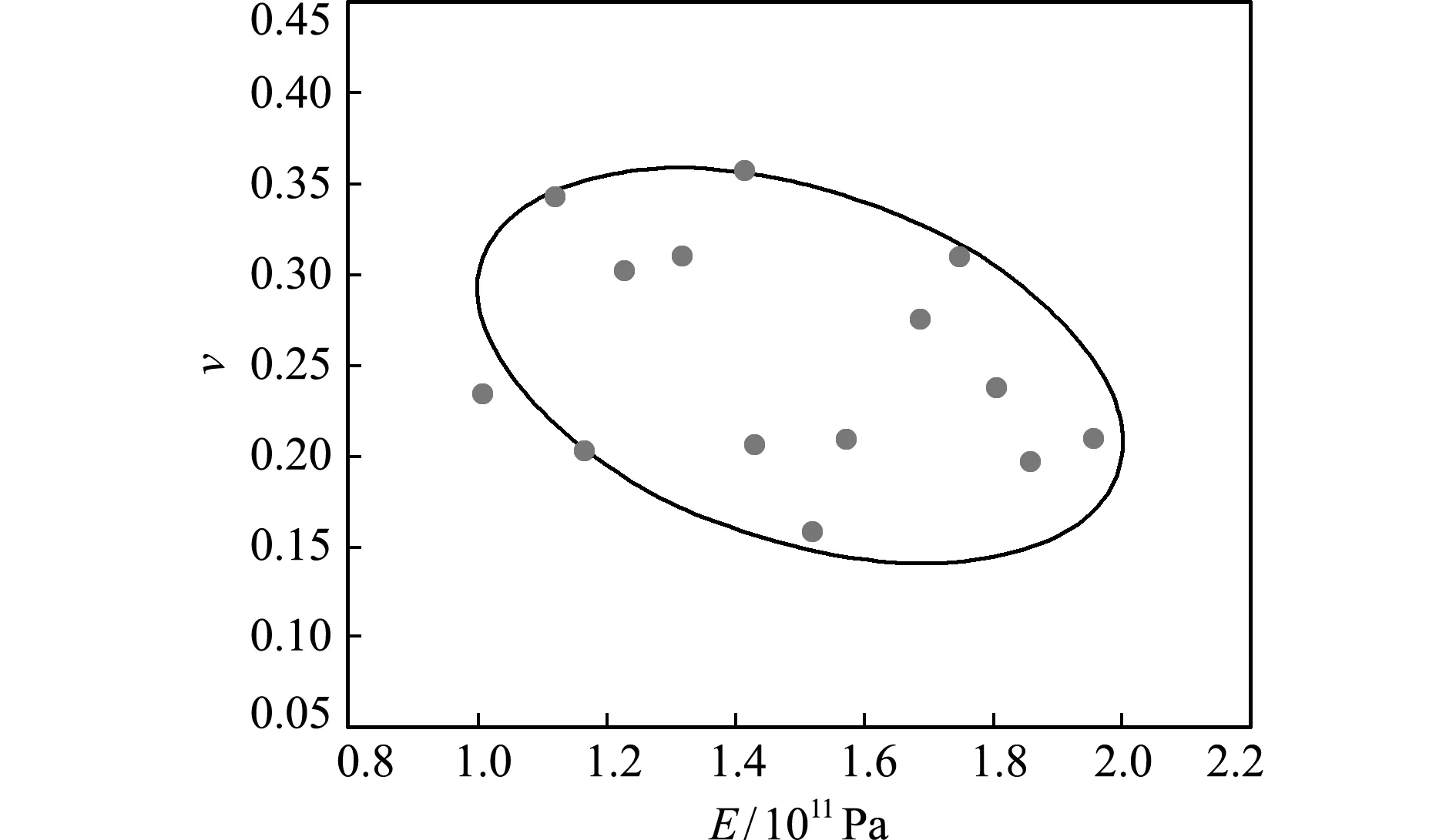
图8 关于椭球域Ω2的减基空间样本点分布

Fig.8 Distribution of sample points for the ellipsoid domainΩ2

图9 椭球域Ω2中MCM减基模拟的数值可靠域

Fig.9 Numerical reliability domain by MCM reduced-basis simulation on the ellipsoid domainΩ2

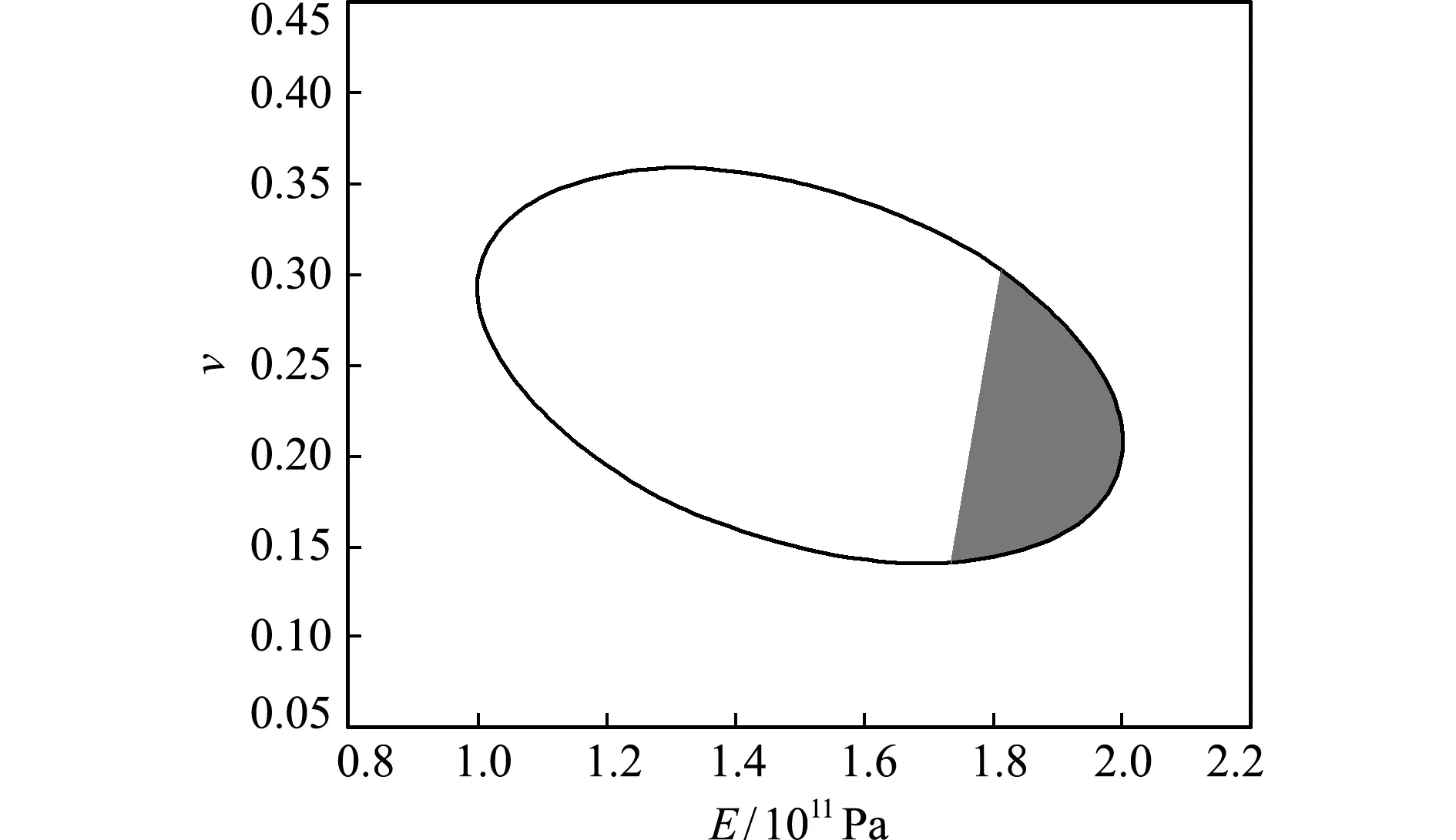
图10 椭球域Ω2中MCM有限元模拟的数值可靠域

Fig.10 Numerical reliability domain by MCM finite-element simulation on the ellipsoid domainΩ2

6 结 论

工程实践中，针对结构可靠性分析过程存在的计算效率低下等问题，基于减基概念提出了一种新的面向椭球域结构的可靠性高效分析方法。通过对结构参数域的坐标正交变换以及参数样本点的坐标逆向变换，构建出椭球域结构的减基空间及其减基计算模型，并在此基础上通过在新坐标系下的等概率抽样以及参数抽样点的标准椭球域判别及坐标逆向变换，实现了可靠性分析的MCM减基模拟。本文的算例测试验证了所提方法能够获得准确的计算可靠度及数值可靠域，并具有较高的计算时效性。此外，本文方法对于结构可靠性分析具有重要的通用意义和实践价值，后续的研究可进一步拓展到有关大型设备和高端装备的可靠性设计等 领域。