基于有限体积法的三维局部冲刷数值模型研究及应用

李登松，戴光清，金 鑫，曾 赟，漆力健

(1.四川农业大学 水利水电学院，雅安 625014；2.四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065；3.成都理工大学 能源学院，成都610059)

1 引 言

水流在流经桥梁墩台、丁坝和河海岸线等水工建筑物时，极易产生局部冲刷，导致水工建筑物的毁坏。因此，局部冲刷的破坏机制和程度一直备受关注，目前主要借助物理模型试验进行研究。大量的试验结果表明，冲刷破坏的主要原因是漩涡和下潜水流[1,2]，其发展大致分为形成初始冲坑、冲坑发展和平衡冲深三阶段[3]。破坏程度主要根据经验或半经验性冲深公式的计算结果进行预测，如Garde等[4]的丁坝冲深公式和Melville等[5，6]的桥台公式。但是试验存在比尺效应，而且难以准确全面地捕捉冲刷坑发展过程和坑内流场信息等。

与物理模型试验相比，数值计算弥补了上述缺点，并且可以预测冲坑地形的演变。目前，数值模型的开发主要基于有限体积法(FVM)、有限差分法(FDM)和光滑粒子法(SPH)等。SPH法根据拉格朗日法求解，将其应用在局部冲刷模拟的过程中则为追踪泥沙颗粒的运动轨迹[7]。FVM和FDM法均是根据欧拉法求解N-S方程，不同之处在于方程的求解形式[8]。在以欧拉法为基础建立局部冲刷仿真平台时，核心问题是水沙(流固)模型的耦合计算，以及水沙运动交界面的耦合处理。水沙模型的耦合包括单向和双向耦合，大多采用单向耦合，如文献[9，10]在模拟冲刷演变的过程中数据传递按照流场(N-S方程)→地形更新(泥沙连续性方程)的方向进行。水沙运动交界面的耦合处理包括动边界法(MBM)和浸入边界法(IBM)。动边界法直接处理运动边界和水沙耦合面[11]，文献[12，13]通过该方法实现了圆柱桥墩和丁坝周围局部冲刷时运动边界的网格重构。

本文以有限体积法和非结构化的计算网格为基础，水沙交界面数据采用单向传递，运动交界面应用动边界法，最终构建了局部冲刷的三维数值模型。应用该数值平台模拟桥墩和丁坝周围的局部冲刷，预测了冲深和冲刷过程中地形的变化，并通过相关研究者的试验结果验证了三维数值模型的可靠性和准确度。

2 控制方程

2.1 三维非恒定水流控制方程

局部冲刷水流为三维非恒定水流，连续性方程和纳维-斯托克斯(Navier-Stokes)方程能较好地进行模拟，控制方程的积分形式如式(1,2)。

连续性方程的积分形式为

(1)

动量方程的积分形式

(2)

N-S方程(2)为瞬时运动方程，按时间平均后为雷诺方程(RANS)。雷诺方程中的切应力项为

(3)

在SSTk-ω紊流模型中，运动涡粘系数νT、紊动能k和耗散率ω分别由式(4～6)计算。

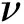
(4)

(5)

(6)

式中F1,F2,S,σk,σω 2,Pk,β*,α,β和σk为闭合系数。

2.2 河床变形方程

在局部冲刷的过程中，水力学条件变化较为迅速，并不会立刻或较大地改变悬移质输沙率。而短时间内河床地形的改变主因为推移质通量变化。因此，忽略泥沙颗粒沿水深方向输移扩散的通量守恒法适用于水工建筑物周围的泥沙输运，满足通量守恒法的河床变形控制方程为

(7)

qB L=qbuB L|ds||δb|

(8)

式中qb为单宽体积推移质输沙率；uB L为平行于床面的速度矢量；ds为单元体面的边缘长度矢量；δb为沿Z坐标轴的矢量，大小为推移质层厚度。

在计算推移质通量时，常用的单宽体积推移质输沙率公式有Meyer-Peter-Muller公式和Van Rijn公式。本文选用Van Rijn公式,即

(9)

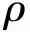
T=(τb-τb,c)/τb,c

(10)

式中τb为床面切应力，本文通过数值计算获取瞬时床面切应力；τb,c为泥沙颗粒起动时的临界床面切应力，该切应力由Shields曲线获取。

2.3 边界条件

边界条件分为水流进出口和壁面。水流进口边界采用速度进口，出口边界采用压力出口。当水流流过固壁边界时，主要涉及壁面上的剪切条件和粗糙度参数。剪切条件是对固壁剪切力的设定，文中移动壁面设定为无滑移条件。粗糙度常数Cs主要由颗粒类型决定，当颗粒类型与均匀沙粒相距甚远时，结果偏差很大，在 0.5～1.0 间调整该值。但是，不存在通用的参数准则适用于任意颗粒类型。由于泥沙冲刷模拟需要泥沙颗粒粒径，因此应用有效粗糙率ks和糙率常数值Cs模拟均匀沙和非均匀沙属性，取值列入表1。

表1 有效粗糙率ks取值

Tab.1 Value of effective roughnessks

壁面类型有效粗糙率ks光滑壁面0非均匀沙粒d50/dm均匀沙粒沙粒高度

此外，临近壁面区域的网格处理精度直接影响附近流场求解结果的精度。因此临近壁面的第一个网格几何中心的尺寸应大于有效粗糙率ks。

k-ω模型的近壁面处理依据以下方法,

∂k/∂n=0, ∂w/∂n=0

(11)

式中n为壁面边界法向量。

在临近壁面边界的第一个网格中心处的值定义为

(12)

式中Cμ为调节湍动粘性幅度的常数,K=0.4为卡门常数,uτ为摩阻流速,yp为第一层网格节点与壁面的距离。

3 空间离散与求解

3.1 河床变形方程的空间离散

根据散度定理离散基于有限体积法的河床变形方程(7)后，该方程变为

(13)

式中AH为网格面投影在水平面上的面积,n为网格面上边缘线的单位外法向量,ie为单元体面的四条边。

由于数据存储于非结构化体网格或面网格的中心，在重构网格面上的通量qB L时，定义中心网格Cell_0和邻近网格Cell_1如图1所示。

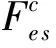
(14)

式中qb,e s为通过面es的单宽体积推移质输沙率,de s为面es的面积(三维)或边缘线长度(二维),uB L为面es平行于床面的速度矢量,n01为网格中心和邻近网格单元的法向量，方向始终由单元Cell_0指向单元Cell_1。

图1 网格面通量重构

Fig.1 Reconstructed flux of grid face

(15)

式中qb,d为中心网格下游的单元体，如图2所示，采用一阶迎风格式判断单元体是上游或下游单元体；(qb)c为中心网格的梯度，根据高斯定理获取，如式(17)；d为中心网格指向下游网格的矢量，大小为两个网格中心的距离。

(16)

式中Ω为单元体的三维体积或二维面积,dS为单元面的面积或二维边缘线的长度。

3.2 沙滑模型

天然河床或者冲坑绝大多数都具有一定坡度，斜坡上的泥沙颗粒存在泥沙休止角，大于泥沙休止角时，失去稳定状态，下滑直至达到新的稳定状态。因此,在更新网格节点位移值时，需要沙滑模型修正床面变形位移值，实现斜坡床面坍塌。

以图3的网格单元C19作为分析对象，阐述沙滑模型。当网格面的坡度超过泥沙颗粒休止角后，调整节点位置，使坡度满足泥沙休止角要求。在C19网格上的节点由邻近四个网格单元共用，节点调整距离ΔZ受到共用网格调整值的影响，调整值由式(17)计算。

(17)

式(17)中，ΔZ19和ΔZ均为未知量，添加泥沙守恒方程(18)使其封闭[14]。

图2 一维非结构中心网格和上下游网格的位置

Fig.2 Location of up and down grids of one-dimensional unstructured central grid and central grid

(18)

式中i为共用邻近网格，A19和Ai为单元面水平投影面积。

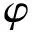
3.3 水沙模型的耦合与求解

在水沙模型耦合时，将计算域单独分为流体域、泥沙固体域和水沙交界面，在流体域内基于ANSYS-FLUENT平台计算水动力控制方程，在固体域内基于用户定义函数(UDF)实现泥沙输移模型和底床变形方程的数值求解，然后将位移变化量赋给水沙交界面。

水沙模型的耦合计算以上一时间步结果作为水沙交界面当前步的计算数据，即采用单向弱耦合，具体步骤如下。

(1)根据上一时间n-1步的水流模块和泥沙模块计算数据，执行当前时间n步底床变形方程的显式数值计算，通过反距离权重系数得到交界单元面上节点的位移值。

(2)根据当前时间n步的位移值，预估交界面任何位置坡度，若超过泥沙休止角，执行沙滑模型，进而调整n步位移值给定最终更新值。

(3)根据最终位移更新值修改交界面地形，重构计算域内网格。若冲淤平衡则停止计算，否则重构后的网格将为下一时间n+1步的水流模块提供边界条件，执行步骤(1)和(2)，直至达到平衡。

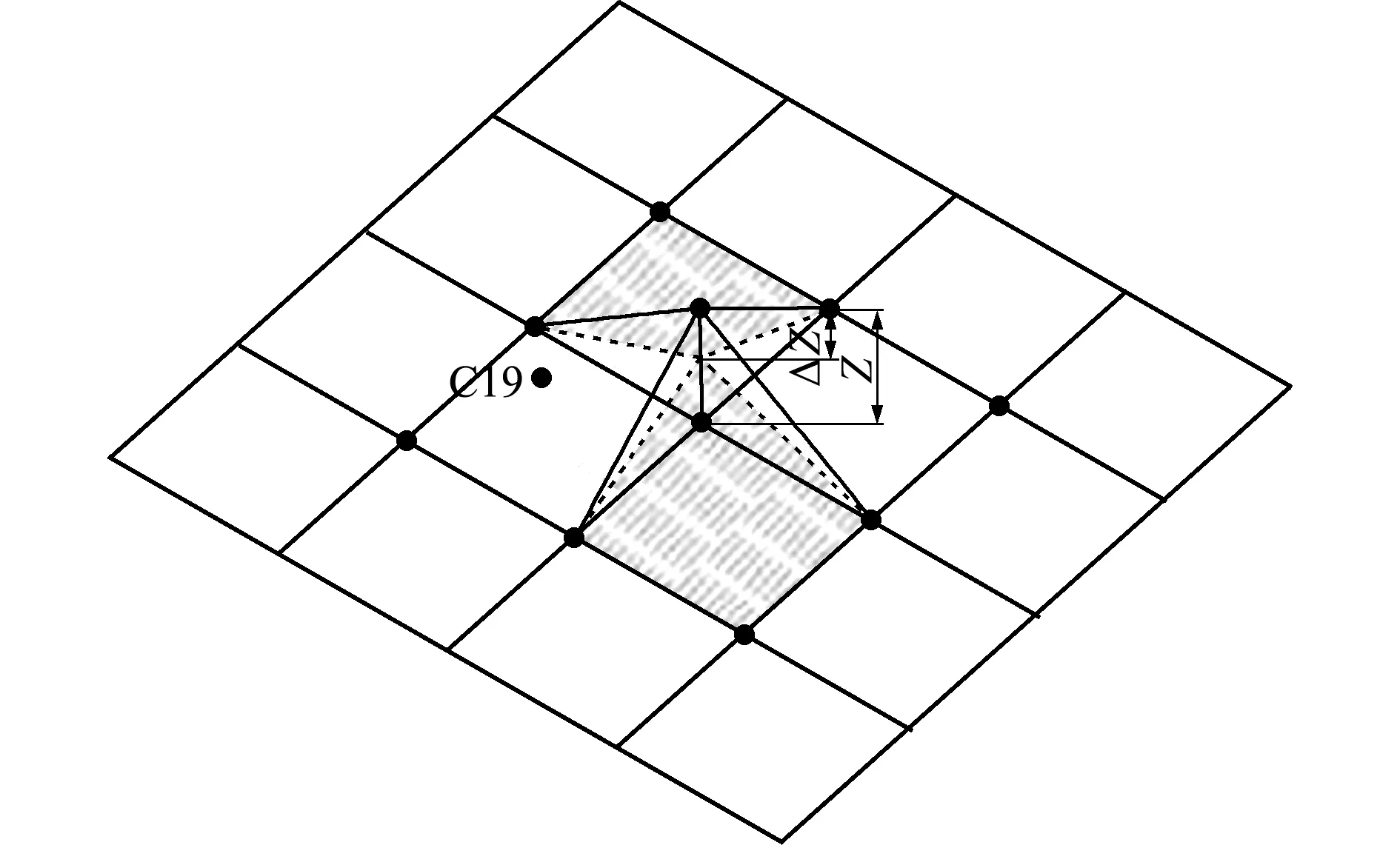
图3 斜坡上泥沙颗粒滑动

Fig.3 Sediment particles sliding on the slope

应用ANSYS-FLUENT用户自定义函数接口(UDF)实现泥沙模块和底床地形变化模块的数值求解后，得到了床面位移的更新值，通过动网格模型中DEFFINE _GRID_MOTION 更新和定义边界运动。

4 模型验证与应用

4.1 Sumer动床圆柱冲刷

4.1.1 模型及工况

模型的可靠性和准确性验证基于Roulund等[15]的动床圆柱冲刷试验。在动床试验中，桥墩的直径为D=10 cm，距离稳定后的水流进口为6.6 m，前方长为3.85 m的底床范围均为动床。试验明渠长为9.9 m，宽为3.6 m。水流行进流速为V= 0.46 m/s，水深H=0.4 m，水流边界层厚度为0.2 m，行进流速与泥沙颗粒起动临界流速比值为1.25，底床泥沙颗粒粒径为d50=0.26 mm。圆柱周围的水流特性和冲刷过程记录采用水下微型摄像机，流速采用DANTEC 2.5 mm。

数值计算域和计算工况与文献[14]的数值试验保持一致，列入表2。

4.1.2 平衡冲深时地形与试验对比

图4为平衡冲深时冲坑形状和Sumer试验的对比。可以看出，通过本文的三维局部冲刷数值模拟得到最终冲坑形状投影至平面为圆形，与试验测量结果吻合良好。

表2 计算工况

Tab.2 Computational conditions

泥沙粒径/mm桥墩直径/m行进流速/m·s-1水深/m0.260.1000.460.2

图4 平衡冲深时冲坑形状和试验对比

Fig.4 Comparison of the shape of the scour hole with the experiment in equilibrium depth

图5为平衡冲深时纵轴线本文数值计算的冲深与Sumer试验测量值和数值计算值的比较。从图5的冲深值比较可以看出，本文数值的圆柱迎水段冲深值大于Sumer试验和数模值，最大误差值分别达到20%和30%，但变化趋势一致，其原因在于本文初始给定的水流稳定段直接影响了迎水段泥沙输移。圆柱尾流后的冲深值与Sumer数值计算值间的误差为5%左右。

4.1.3 冲刷坑内水流特性与试验对比

由于Sumer的动床试验未测量冲坑内水流特性，与Unger等[16]的试验测量结果定性比较分析轴对称面圆柱迎水端冲坑内不同时刻的流场特征，如 图6 所示。可以看出，冲坑发展时坑内流场表现的特征基本与试验测量结果吻合。在初始时刻，如图6(a)所示，近底床附近的涡旋和下潜水流以及近自由水面的上升趋势均有捕捉；在冲刷发展一段时间后，如图6(b)所示，冲坑从圆柱边界逐渐向后发展，形成了一定的坡面，整体坡面角度均小于泥沙休止角，且坑内水流为明显的下潜水流，与Unger试验测量结果一致，Unger分析后指出此阶段的下潜水流偏转至圆柱横向两侧，加剧此处泥沙的冲刷；当冲刷继续发展时，如图6(c)所示，冲坑内形成了明显的涡旋，近床面附近的水流下潜趋势也明显。此外，从自由水面在整个冲刷演变过程中的发展可以看出，靠近圆柱附近的水面上升趋势未 改变。

图5 纵轴线数值计算的冲深与Sumer试验测量值比较

Fig.5 Comparison of the numerical depth of the longitudinal axis with the experimented by Sumer

图6 轴对称面数值计算的冲坑内流场(左)与Unger试验(右)比较

Fig.6 Comparison of numerical calculation(left)and Unger’s experiment(right)of the flow field of axisymmetric plane in the scour hole

根据冲坑内水流特性与试验的定性比较，可以认为本文建立的三维数值局部冲刷模型能准确模拟冲坑内水流发展。

4.1.4 三维冲刷坑的演变结果分析

圆柱局部冲刷在不同时刻的三维冲坑地形如图7所示。可以看出，地形演变特征如下。在初始发展阶段，即T≤50 s时，圆柱上游的冲坑形状接近半圆形，斜坡斜率小于或等于泥沙休止角，在圆柱下游的泥沙淤积成类似坎的形状；随着冲刷持续发展至T≤1230 s，冲坑内水流表现出图6(a)的特性后逐渐演变为图6(b,c)所示的特性，由于下潜水流偏移至圆柱两侧导致冲坑横向扩展和纵向逐渐冲深，最终形成了圆形冲坑，坑内的泥沙带走后大面积淤积为舌状，当水流演变为下潜水流和涡旋共同作用后，水流持续冲刷冲坑底部，使得冲坑横向和纵向范围扩大，且伴随斜坡坍塌形成倒锥形坡度，坑后淤积泥沙向圆柱横向和下游扩散；当冲刷发展至T=2415 s时，即将达到稳定状态，此时冲坑范围扩大趋势减小；当冲刷发展至T=3600 s时，达到稳定冲深阶段，深度增加值和范围基本保持稳定，床面泥沙冲淤达到平衡状态。此外，在整个过程中能较为清晰地观察到初始时下游和水流入口段形成的堆积泥沙(沙丘)逐渐迁移发展的演变。以上总结的演变特征与Sumer试验过程中观察到的演变特征一致。

图7 不同时刻的冲深地形

Fig.7 Topography of scour hole at different times

经过上述动床冲坑演变、冲深变化和坑内水流特性可以看出,本文建立的三维局部冲深数值模型的准确度能满足要求。

4.2 Michiue动床丁坝局部冲刷试验

4.2.1 模型及工况

采用Michiue等[17]在明渠水槽中的非淹没正交丁坝局部冲刷试验进一步验证数值模型准确度。试验水槽长为7 m、宽为0.4 m，坡度为1/300；流量为0.004 m3/s，平均水深为2.85 cm，行进流速为 0.351 m/s；泥沙为均匀沙，中值粒径为0.6 mm。丁坝尺寸长为0.1 m，宽为0.01 m。数值计算的区域长为8.0 m、宽为0.4 m、高为0.3 m，如图8所示。

4.2.2 平衡冲深时地形与试验对比

图9比较了丁坝冲刷数值计算地形与Michiue的试验测量值。可以看出，在丁坝背流侧，数值计算的冲刷坑形态与试验测量基本一致，计算的最大冲刷深度平均达到了5 cm；在丁坝坝头位置，冲刷坑的外围形态均表现为长舌状；但数值计算的最大冲刷深度仅位于坝头，试验测量值则延伸至迎流侧的上游约15 cm处，其原因是由于数值计算模型中添加的沙滑模型导致斜坡面满足泥沙休止角后就处于稳定状态，不再受到冲刷，使得此处与实测值存在一定偏差。图9中，丁坝的计算最大冲刷深度约为8 cm，试验测量值为9 cm，两者的误差为11%。此外，数值计算结果沿y方向的扩展比测量值大，这种趋势与文献[14，18]数值计算的丁坝冲刷时得到的冲刷范围明显比实测范围大的结果 相似。

图8 数值计算域示意

Fig.8 Schematic diagram of numerical calculation area

4.2.3 三维冲刷坑的演变结果分析

图10为丁坝周围局部冲刷演变示意。可以看出，丁坝冲刷至时间T=50 s时的时间段内为初始冲刷发展阶段，且初始位置始于迎流侧和坝头，带走的泥沙分别向坝头的冲坑外围和坝后淤积成由两道梁汇成的舌状体；随着水流持续冲刷至 550 s 时，冲坑范围持续性的扩展变大，坝后舌状堆积体逐渐往边墙附近移动，丁坝迎流和背流侧的冲坑均往外后退扩展至边墙；当冲刷至1050 s时，坝后的淤积形态和坝头冲坑地形形态基本不再发生变化，此时迎流侧靠近边墙的冲坑斜坡面继续冲深；当冲刷至2300 s和3600 s时，丁坝冲刷的最大冲刷深度误差接近0.2%，冲坑整体形态保持稳定，即冲刷达到稳定冲深阶段。

图9 冲刷数值计算地形与Michiue试验实测值比较(单位:cm)

Fig.9 Comparison of numerical calculation and Michiue’s experiment of the topography of scour hole(unit:cm)

图10 丁坝周围不同时刻局部冲刷坑的地形

Fig.10 Topography of local scour hole around dike at different times

5 结 论

基于有限体积法和非结构化的计算网格建立了包括三维非恒定水流、泥沙输移和河床变形方程等控制方程的局部冲刷三维数学模型。应用ANSYS-FLUENT软件模拟三维非恒定水流，利用用户自定义函数接口(UDF)二次开发实现泥沙输移和底床变形方程的数值计算，并结合动网格技术重构变形网格，最终实现了局部冲刷的三维数值模拟。主要结论如下。

与文献[14]的圆柱动床局部冲刷试验以及文献[16]进行的丁坝局部冲刷试验结果对比后验证了该三维模型的可靠性，并成功模拟了局部冲刷过程中地形的变化、最大冲深位置和平衡冲深时的最终地形。

以切应力观点为基础建立的三维局部冲刷数值模型，因数值计算过程中切应力较易获取，具有简易性和较强的可靠性；在利用有限体积法开发类似的局部冲刷数值模型时，单元体泥沙通量重构和坡度影响下,泥沙颗粒起动、输沙率计算以及网格重构过程中坡度修正等均影响数值模型的精度。

在地形变化导致网格更新时，ANSYS-FLUENT提供的动网格模型基本能满足体型较为简单的工程(如本文圆柱桥墩冲刷和丁坝冲刷等)局部冲涮大变形区域网格更新需求。但对于体型复杂的工程问题已不再适应，应开发相应的网格重构替代模型。