基于CUDA的有限元矩阵并行装配算法研究

胡斌星，李新国，孙 鹏

(1.西北工业大学 航天学院，西安 710072；2.西北工业大学 空天飞行技术研究所,西安 710072)

1 引 言

随着航天运载器广泛采用轻质复合材料和升力体的气动布局等因素，其刚体和弹性体的模态耦合问题愈发突出[1]。传统的方法是将箭体视为柔性梁分析[2,3]，将助推器也视为一维梁与芯级组成空间梁系，基于特定的小偏差增量模型分析弹性振动对控制系统的影响[4]。而在高超声速飞行器的分析中也常以均匀分布质量的自由梁[5]或悬臂梁[6]建模来分析其与气动和推进系统的耦合关系。随着现代航天理论与相关行业技术的推进，航天运载器技术从一次性运载火箭向可重复使用运载器过渡，同时对新一代飞行器提出重复使用、健康监测、故障诊断和任务重构的要求。将弹性问题从三维空间简化为平面问题虽克服了计算的困难，在工程上也得到了验证，但在很多情况下，这种简化将会导致较大的误差。如飞行器在飞行过程中产生滚转时，需考虑结构的扭转弯曲作用；简化的非均质梁在载荷不均匀时，按平面柔性梁进行简化误差较大[7]；简单的一维梁模型解析解无法模拟运载器各部位的应力应变以实现健康监测，也无法通过传感器所测的结构损伤程度计算当前极限过载以重构制导指令，无法达成任务重构的目的。

限制采用有限元模型的因素主要是其仿真计算速度较慢，且单元刚度矩阵、组装和总刚度矩阵的计算均较为耗时，尤其当飞行器本身构建单元数量较大时，无法在一个或几个制导周期内完成结构强度的校核。目前，GPU计算在有限元分析中的应用尚处于初级阶段[8]。许栋等[9]针对浅水问题利用GPU完成了多达112倍的加速比，并对核函数参数进行了优化分析；曾良等[10]通过共享内存边界的迭代法，实现了流体计算的加速问题；Cecka等[11]针对热传导问题的有限元并行组装进行了深入研究；Dinh等[12]则对GPU的有限元实时仿真问题做了一定研究，并总结了COO(Coordinate)格式下的单元组装问题；Dziekonski等[13]讨论了在多GPU环境下，大型系数线性方程的生成问题。

本文结合目前主流飞行器构型，利用GPU浮点运算能力极强的特点，着重从单元刚度矩阵的并行组装方面进行详细研究及设计，为实际的飞行仿真及任务提供技术验证。

2 有限元矩阵并行装配算法设计

在有限元法求解步骤中，单元刚度矩阵完成计算后下一步就是装配总刚度矩阵，建立总平衡方程组以求解节点位移。当节点数目较多时，总刚度矩阵的阶数也较大，由于计算机内存的容量限制，有可能无法按照传统方法进行存储，在ANSYS中采用波前法[13]，即边分析边消去以避免总刚度矩阵的生成。不过鉴于波前法需频繁交换CPU缓存和内存的数据，限于内存带宽，在求解较大规模问题时往往较为费时[14]。同时，由于存在大量的内存拷贝和索引量操作，装配步骤在大型有限元模型的整体求解耗时中也占有相当比重。下文在内存能够完全容纳总刚度矩阵的假设下，设计总刚度矩阵的并行算法。

2.1 有限元矩阵装配并行性分析

总刚度矩阵根据单元类型的不同分别计算每个单元局部坐标下的刚度矩阵，经局部坐标系下的单元刚度矩阵转换到整体坐标系下后对号入座完成装配。

[K]=∑[Ke]

(1)

由于邻近单元共用某个节点，且可能在单元刚度矩阵中的位置一样，则总刚度矩阵的装配不能单纯以单元向量形式并行化，否则可能出现相同地址的访问冲突，进而造成计算结果错误。当且仅当每步并行装配没有共同节点的若干个单元的刚度矩阵，或至少保证每步中所有单元矩阵在总刚度矩阵中的位置不一时，并行装配才得以实现。从实际出发，有如下方案。

(1)每次同时装配一个单元刚度矩阵中多个位置的元素。

(2)每次同时装配若干个单元刚度矩阵中同一位置的元素。

(3)每次同时装配若干个单元刚度矩阵中若干位置的元素。

在单元刚度矩阵计算阶段，每步均是以长度为r的向量形式对单元刚度矩阵中的某个子块的某一处元素并行计算，由此可推断每步装配能同时计算r个单元的分块单元刚度矩阵中块[Ki,j]中(p，q)处的元素。而当r为单元总数时，并行装配的每一步即为叠加所有单元的单元刚度矩阵中同一位置的元素。于是可提出，在何种情况下可同时装配所有单元刚度矩阵同一位置处的元素满足访问冲突的要求，即如何保证总刚度矩阵中所有位置的元素在每一步装配中均只受一个单元影响。结合GPU架构，适用于其SIMD架构的组装算法应添加以下几点关键思路。

(1)将任务分成若干个相互独立的子块，子块间应不存在对同一地址的访存冲突。

(2)尽量减少全局内存的数据传输量，且尽量满足内存的合并访问，提高分级内存体系下的数据重用和访问效率。

(3)平衡数值计算和数据流间的效率。

(4)尽量优化每个线程块内线程数和流处理器内的可用线程块数目。

基于CUDA的并行组装算法的难点在于，如何保证单元核函数高效地获取节点数据并将单元数据组装至系统方程。合并读取和写入全局内存并且避免共享内存访存冲突在没有显著耗时的输入数据重构的条件下几乎不可避免。此外，通常多个单元共享某一个节点，则说明其共享自由度，故在整个并行计算中应该尽量避免全局同步机制和原子操作以期避免竞态条件[15]。在此之前，文献[16，17]介绍了FEM中稀疏矩阵的并行组装问题,提出每个线程对应计算系统方程Ax=F的每一个非零值，以避免竞态条件；然而，该方法需要每个线程计算单元子程序并从每个贡献单元的数据中提取相关条目，因此，该做法会导致很多的冗余计算。如果ef是每个单元的自由度数，则单元子程序需要调用(ef+1)ef次(前一项表示对每个非对称矩阵 中的非零项，后一项表示在Ae的非零项)。尽管单元特征矩阵的计算过程因单元特性而异可能计算开销并不大，但多次从全局内存中检索单元子程序所需的节点数据，而非以合并访问的方式进行，则时间开销非常大。

考虑组装算法的通用性，暂且认定单元矩阵的形式不一，仅认为单元子程序作为黑箱在每个线程或线程块内运行，实现组装过程与单元特征矩阵计算的分割独立。文献[18]表明，该方案适宜于低阶单元并取得了较好的加速比，同时基于该思路针对高阶单元的优化在文献[19]中也已有阐述。则在确定单元特征矩阵与装配过程解耦后，即确定装配形式，即GPU内的线程或线程块与矩阵中元素间的关联，如某一个某一行(列)、非零元素或非零项子集等。同时，考虑可用的GPU资源，由于其包含了三种分级内存系统[20]，可得到如下基于GPU架构的典型并行方案。

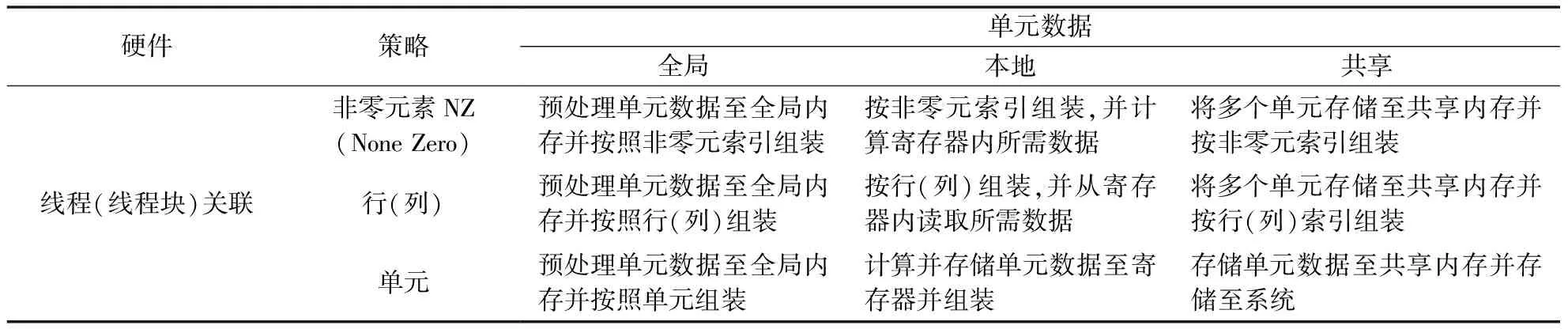
表1 数据的存储与硬件资源的关系

数据存储-线程关联的组装策略列入表1，每种方案均有其优劣，其中文献[18]阐述了基于本地寄存器的NZ组装算法、全局内存的行组装算法以及基于不同颜色区分的单元组装算法。故下文主要阐述各并行装配算法在GPU上的实现及优化,其中第一部分详细描述依照颜色划分单元的装配策略，保证两个线程不会同时写入某一相同内存地址的具体实现；第二部分阐述第二种算法，即将计算分为两部分，计算所有的单元数据并存入全局内存，接着组装所有的单元数据至矩阵A；第三种算法较前两种更复杂，使用了共享内存以减少全局内存的通信量,节点和单元皆分割成若干个子集，每个子集调用若干线程计算单元特征矩阵并计算单元在系统方程内相应的位置。方案三能够减少节点数据的总读取量，避免了单元数据的重复执行并减少了全局内存的写入量。

2.2 并行装配算法

2.2.1 以颜色分组的组装策略

避免竞态条件的直接方法是在组装算法前对网格单元进行着色预处理，使得任意两个相同颜色的单元不共享自由度，如图1所示。尽管确定一个模型的最小着色数是一个NP(Non-deterministic Polynomial)完全问题，但已有多种启发式算法[21,22]能够找到近似的最小着色数。

本文选用网格的对偶图的顶点着色，其中每个单元代表图中的节点，两个节点若通过一条边相连则表示两个单元共线或者共面。需注意应保证每种颜色的单元数目尽量相近，因为在CUDA中各流的数据量和计算量尽量相同才能发挥流的最大作用[23]；同时，若某种颜色的单元数量不足可能启动较少的线程块，进而导致GPU资源的低效使用。

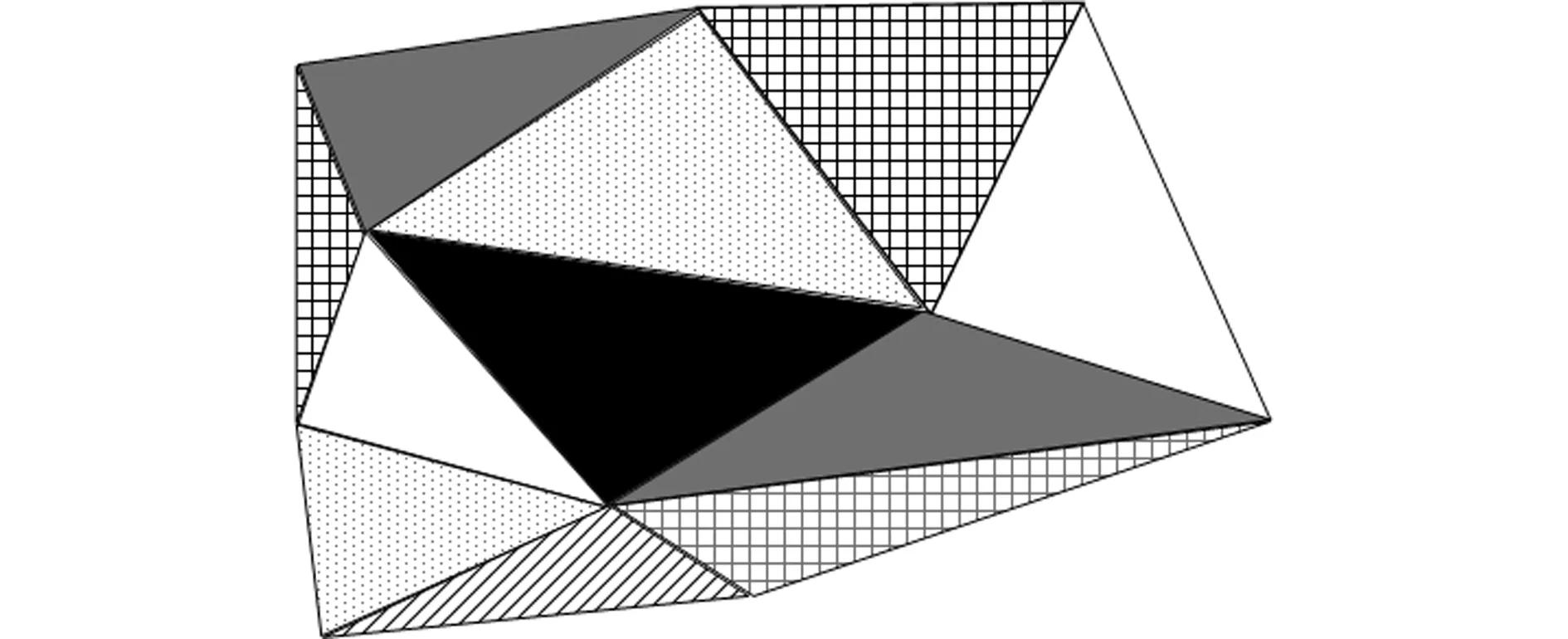
图1 2维单元着色

Fig.1 2-D element coloring

在此，不妨将着色为k的单元集合写做εk。在集合εk中单元之间不共享节点，所以不用优化从全局显存中读取的每个单元的节点数据。相反，每个元素从全局内存中检索自己的节点数据，运行单元核函数计算单元刚度和质量矩阵，并将该数据组装至系统方程。则预处理每个着色的单元矩阵Ek为

Ek(σk(e),a)=E(e,a)

(2)

σk:εk→{1,…,|εk|}是全局单元号至着色单元号的映射。这些矩阵放置在内存中，线程对应单元内存的合并访问。每个着色为k的组装核函数流程如下。

(1)Tid←globalThreadID;

(2)For alln∈[1,en]do

(3)Nodes[n]←C(Ek(tid,n))

(4)End for

(5)计算(Ae,Fe)=elem(nodes)至系统方程

在上述算法中，步骤(5)取决于稀疏矩阵的存储格式。为保证程序的通用性，在此提前计算本地单元数据至目标系统方程的索引数组中。为保证读取的合并访问，数据格式安排如图2所示。一个列主元矩阵存储每个单元的节点号(灰色部分)，其后表示每个单元数据与系统方程的映射关系(白色部分)。假定有一个一阶线性三角单元，可知矩阵的列数为三个点的坐标数据加上6个单元特征矩阵Ae及3个等式右端的Fe项。

2.2.2 使用全局显存的非零项组装策略

该策略采用一个线程(或线程块)计算一个有限单元数据，为避免竞态条件，先将单元数据写入全局显存以便稍后的系统方程构建。受GPU硬件架构的限制，全局显存内的单元数据在构造系统方程时无法执行全局的同步操作，故组装系统方程和计算单元特征矩阵需执行两个不同的核函数。鉴于篇幅，针对全局显存的非零项组装策略仅介绍单元特征矩阵的核函数并行计算部分。

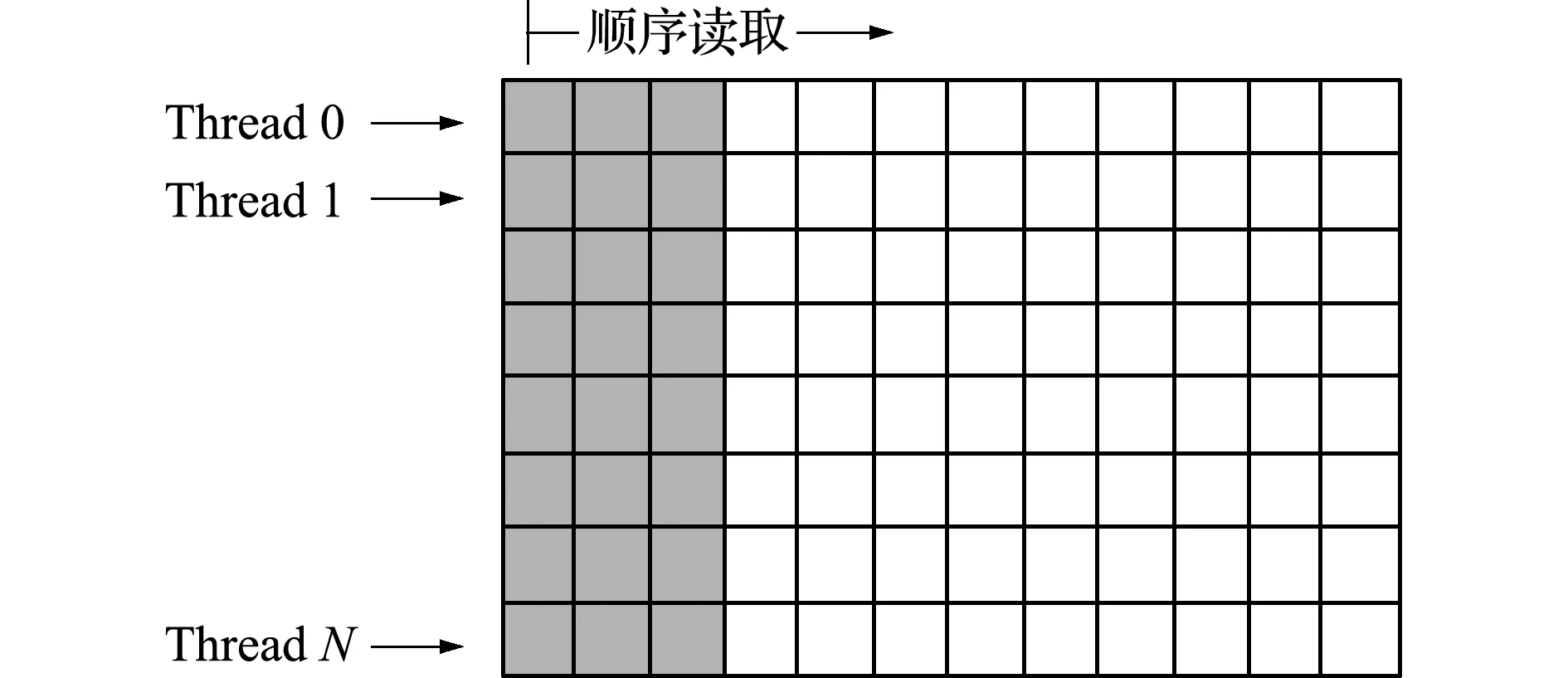
图2 单元数据及其附加映射数据在GPU内存存储格式

Fig.2 Storage format of unit data and its additional mapping data in GPU memory

在一般情况下，因单元内节点编号并不连续，而节点结构体数组通常是按编号排序的，故通常在读取该部分数据时无法实现合并访问。在此不妨设置一个节点数据矩阵Ce，其中，Ce(e,a)是单元e的本地节点a的节点数据。如果节点数据不发生变化，则可实现加速；若节点数据发生变化，则Ce需在每个时步进行更新。与上述算法对比，本策略中Ce刷新需要额外的全局显存带宽，通常会导致计算速度更慢。故可将单元组织为若干个子集，其中子集内的单元可以共享节点数据，使得经由全局显存的数据传输总量通过预取数据实现线程块内的数据共享。在此，不妨假定εk是第k个线程块的单元集合，计算节点集合Nk的公式为

Nk={E(e,a)∶e∈εk(a=1,…,en)}

(3)

线程块k需检索其对应的单元子集εk，然后该单元子集所需的节点数据经全局显存存入共享内存。由于GPU内的共享内存有大小限制，为确保核函数不会调用失败，Nk有如下约束。

(4)

SharedMemSize是以字节数表示的共享内存大小，Dn是单节点的数据大小，无论单双精度均转换成字节即可获得Nk的上限。对后续章节可能存在的非线性及多步插值问题，|Dn|=nd+nf，其中nd表示坐标数据nf牛顿-辛普森迭代的中间值或多步插值中出现的半步长中间量。

确定了满足公式(4)的Nk后，即可将单元分为若干等分子集。选用图论的划分方法，保证每个单元是图中的一个节点，若相应的单元间共面则在两节点间添加一条连线。METIS[24]提供了较优的划分算法，保证得到一个可接受的Nk值。待Nk经计算确定，即可将节点数据存储至共享内存并在单元子程序内参与计算。对于每个线程块k，预处理块单元矩阵Ek定义为

Ek(e,a)=σk(Ek(e,a))(∀e∈εk,a=1,…,en)

(5)

式中σk∶Nk→{1,…,|Nk|}表示第k个块内全局节点号E(e,a)至块节点号Ek(e,a)的映射向量，存储在共享内存中并用于索引节点数据。在每个线程块k内，若干个en维元组连续存储以便全局显存读取的合并访问；待完成后便得到一个blockSise行的列主元矩阵，如图3所示为一个en=3的示意图。一个线程读取索引表后即可将共享内存内的节点数据指向所需的单元子程序；随后，单元子程序计算完单元特征矩阵，并将其以合并访问的方式回传至全局显存。

2.2.3 使用共享内存的非零项组装策略

共享内存较寄存器更大，其访问延迟较全局内存低得多，且块内线程间可以共享单元数据以减少子程序对数据调用的总时长，故提出块内线程处理某一节点子集的思路。假设N是所有节点的集合，有Nk⊂N，于是有单元集合εk为

εk={e∈ε∃a,E(e,a)∈Nk}

(6)

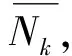
(7)

(8)

式中|Dn|是输入节点数据的尺寸，|De|是单元子程序生成的单元数据Ae和Fe的大小。对于非线性问题,若采用高阶项模拟，假定一个单元内的任意节点有nd个自由度和nf个中间量，可推导

|Dn|=en(nd+nf)

(9)

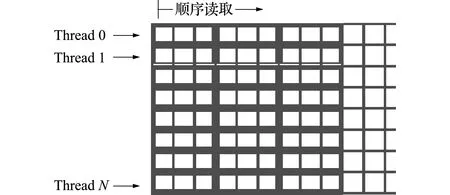
图3en=3的列主元预处理块单元矩阵EI

Fig.3 Column primary element matrix ofen=3

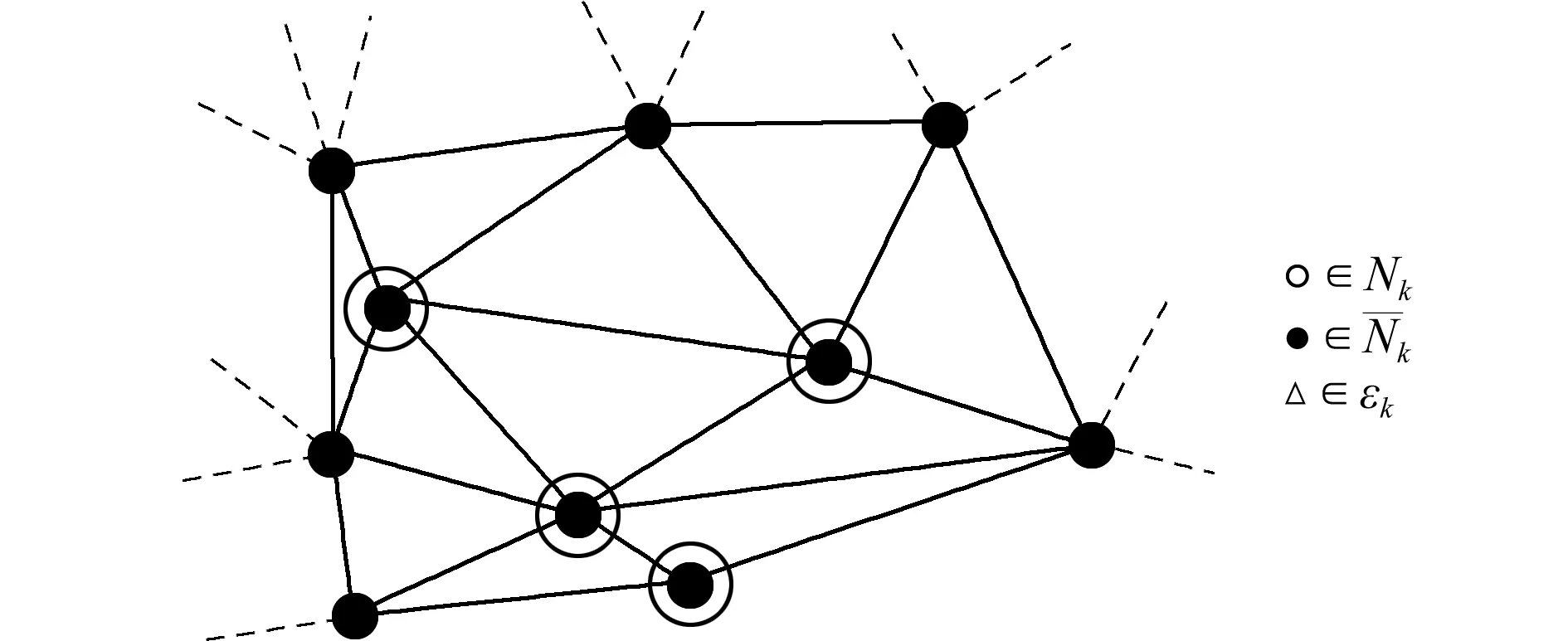
图4 节点集合Nk与其对应单元集合εk

Fig.4 Node setNk-cell setεk

此外，|De|=ef(ef+1)，该参数是本地单元矩阵Ae和力向量Fe的尺寸。考虑单元特征矩阵的对称性，则有

(10)

式中n*因单元维度和形状而异。

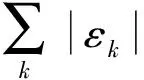
同时，由于单元之间共享节点，最优的也是最重要的优化措施是所有的节点数据仅从全局内存中读取一次，否则会出现多个单元多次读取某节点数据，可能出现访存冲突，也使得计算的实时性无法保证。因此，与全局内存的非零组装算法不同，在此以节点数据为导向作为源索引，其后存储共用该节点的单元，进而形成列主元的归约矩阵，如图5所示。其灰色部分表示全局节点号，白色代表共用该节点的单元列表。区分两种不同索引的方式参考了Cris等[11]的策略,为区分这两部分整数索引，通过反码再减1的方式表示目标索引，通过加1表示目标源索引；程序内每个线程先判断整数的正负号，依据正负号区分两种索引类型。随着线程依次读取列表内数据，将所有指向源向量S的数据累加并存储至目标向量T的目标索引，如下，

(1)Fori:NZ_Reduction

(2)Ifi>0

(3)t←t+S[i-1]

(4)else ifi<0

(5)T[-i-1]←t

(6)End if

(7)End for

其组装方式如图6所示。对于常用的低阶单元,其单元矩阵尺寸较小，辅以节点为索引作为输入量，使得划分的单元集合尺寸较大，理论效率较高。可以看出，在预处理阶段如果Nk内部分或所有节点号连续，有些全局内存的读取也是可以合并访问的。同时,为避免共享内存的存储体读取冲突，分配给每个单元的共享内存地址不能连续。

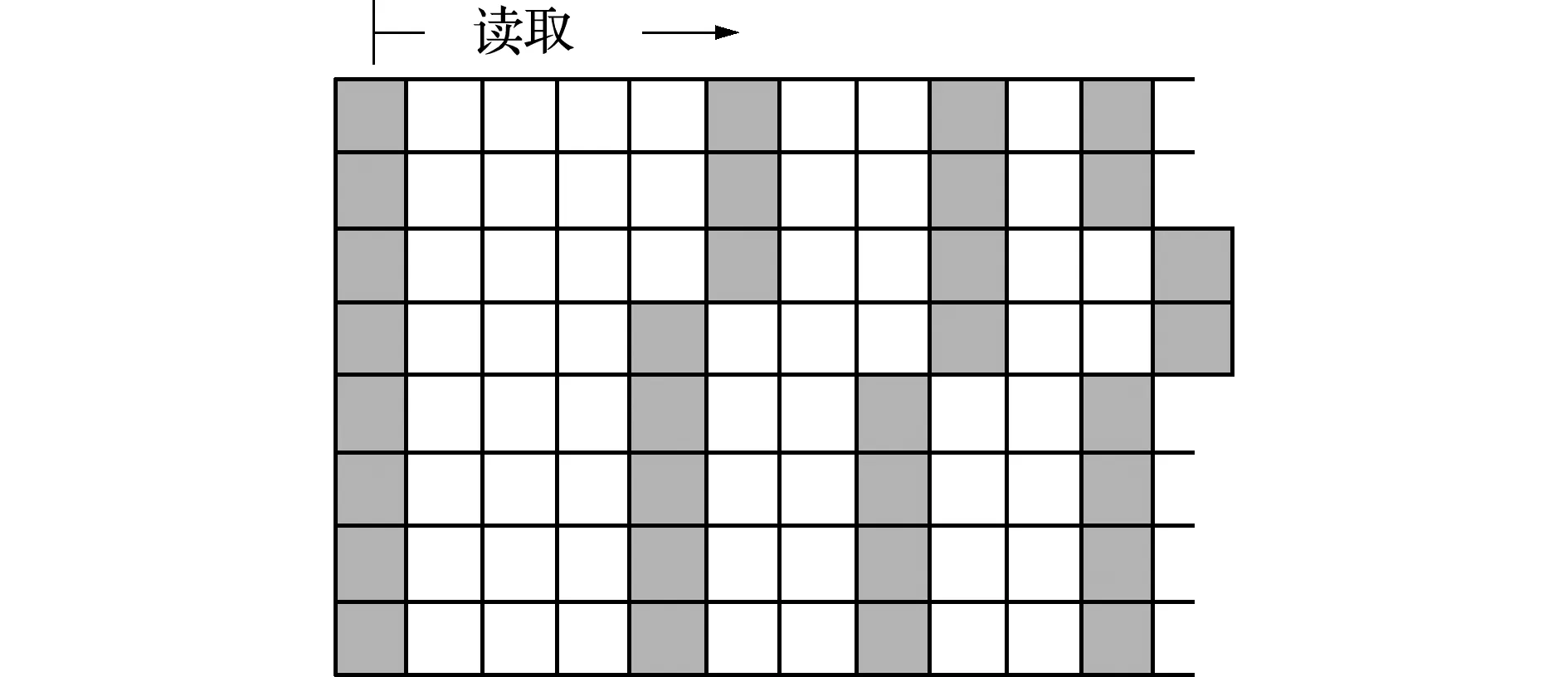
图5 线程块内blockSize行的列主元形式存储的归约矩阵

Fig.5 Reduction matrix stored in column primitive form of block size row

3 并行组装算法算例对比

3.1 测试平台与对象

本文测试平台硬件选用单机多GPU工作站，采用上述算法在自行设计的并行求解器框架下，模拟细长体弹性飞行器飞行过程，并对单GPU及多GPU并行的性能及拓展性进行对比，列入表2。因为CUDA 9.0版本不支持Visual studio新版本的一部分宏，为避免自行配置发生未知错误，在保证支持编译C++11标准的编译器中选择MSVC14.0。为进一步验证单机多GPU节点的耗时情况，带*号的GPU1作为添加的另一部GPU，以期实现单计算节点的并行任务分割。

同时，鉴于Windows并非真正的实时操作系统，其CPU端计时器精度仅有1 ms，故在进行时间统计时采用CUDA自带的cudaEvenet_t计时，其精度为0.5 μs。若干组适宜于航天器典型构型或特征的测试算例列入表3。

3.2 计算精度及效率分析

首先，测试METIS对于单元分类的计算耗时情况。在使用Release且不进行优化，网格从文件中读取的情况下,测试颜色分组耗时，各算例情况如图7所示。可以看出，因为文件读取内容没有变化，I/O耗时基本没有太大变化，几乎是随着单元数目的增加而线性增加。但是两种划分方式随单元数目的变化有着非常大的变化,红黑树在前几个单元数量较少的算例中表现优异，但从编号3开始,K路划分的耗时增幅相对较少；当单元数达到80000左右时，两者在划分成22种颜色的情况下耗时比已达到2.5倍左右。从划分颜色数量的变化趋势看，划分的颜色越多，边切割数越多，必然导致耗时越多；但是若在只有一部图形处理器的工作站上，没有必要划分很多种颜色进而产生非常多的流，那么在4～10种颜色划分中其耗时变化不大，尤其在单元数较多时波动不超过5%，也验证了Cris[11]的观点；而在若干台、每台均有多于一部图形处理器的工作环境下，在编号6中单元数较多时，其额外耗时不超过6 ms，相较于集群计算的通信延迟是能接受的。可见，在此使用METIS进行颜色分组是非常高效和合适的方法；同时，也能通过曲线拟合的方法，在已知单元数目条件下，选择最优的划分算法。

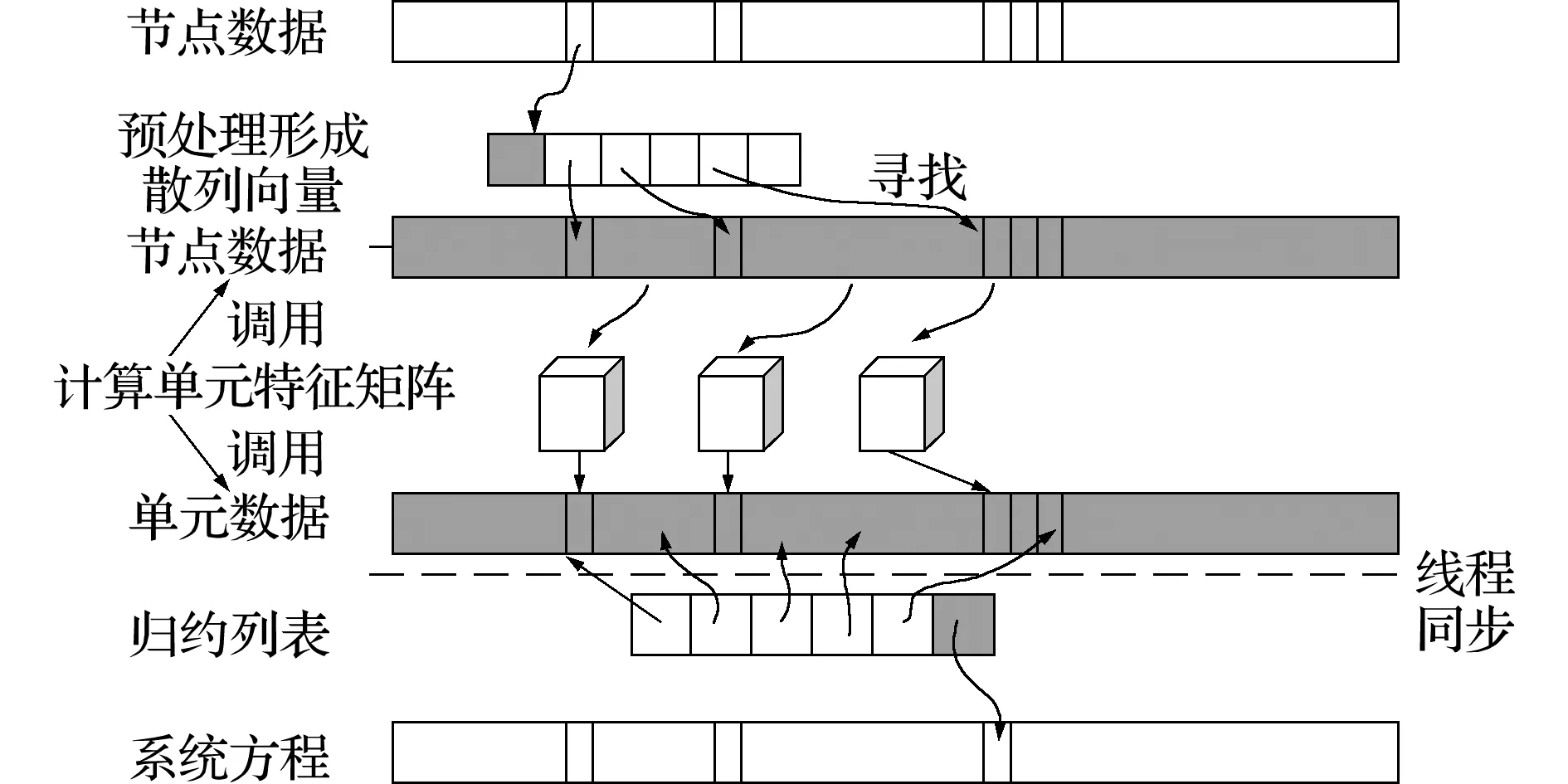
图6 利用共享内存的非零值组装策略流程

Fig.6 Flow chart of non-zero assembly strategy using shared memory

表2 计算平台配置

Tab.2 Computing platform configuration

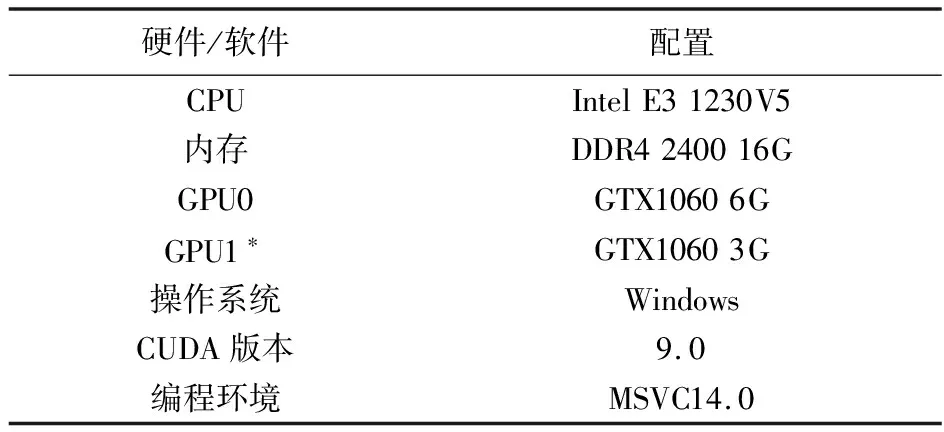
硬件/软件配置CPUIntelE31230V5内存DDR4240016GGPU0GTX10606GGPU1∗GTX10603G操作系统WindowsCUDA版本9.0编程环境MSVC14.0

表3 飞行器典型构型或部件算例

Tab.3 Typical configuration and components list of aircraft

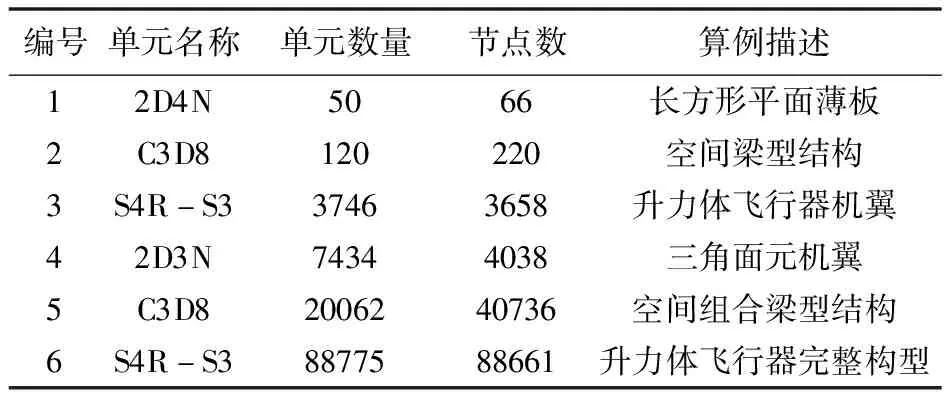
编号单元名称单元数量节点数算例描述12D4N5066长方形平面薄板2C3D8120220空间梁型结构3S4R-S337463658升力体飞行器机翼42D3N74344038三角面元机翼5C3D82006240736空间组合梁型结构6S4R-S38877588661升力体飞行器完整构型

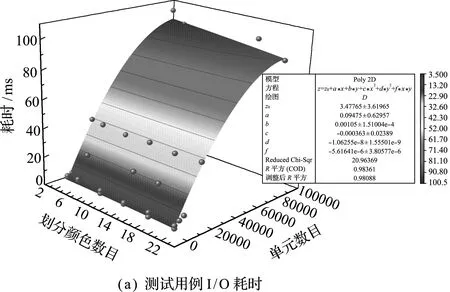
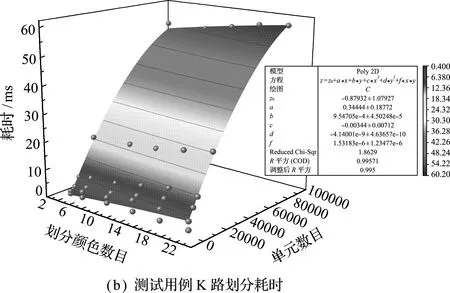
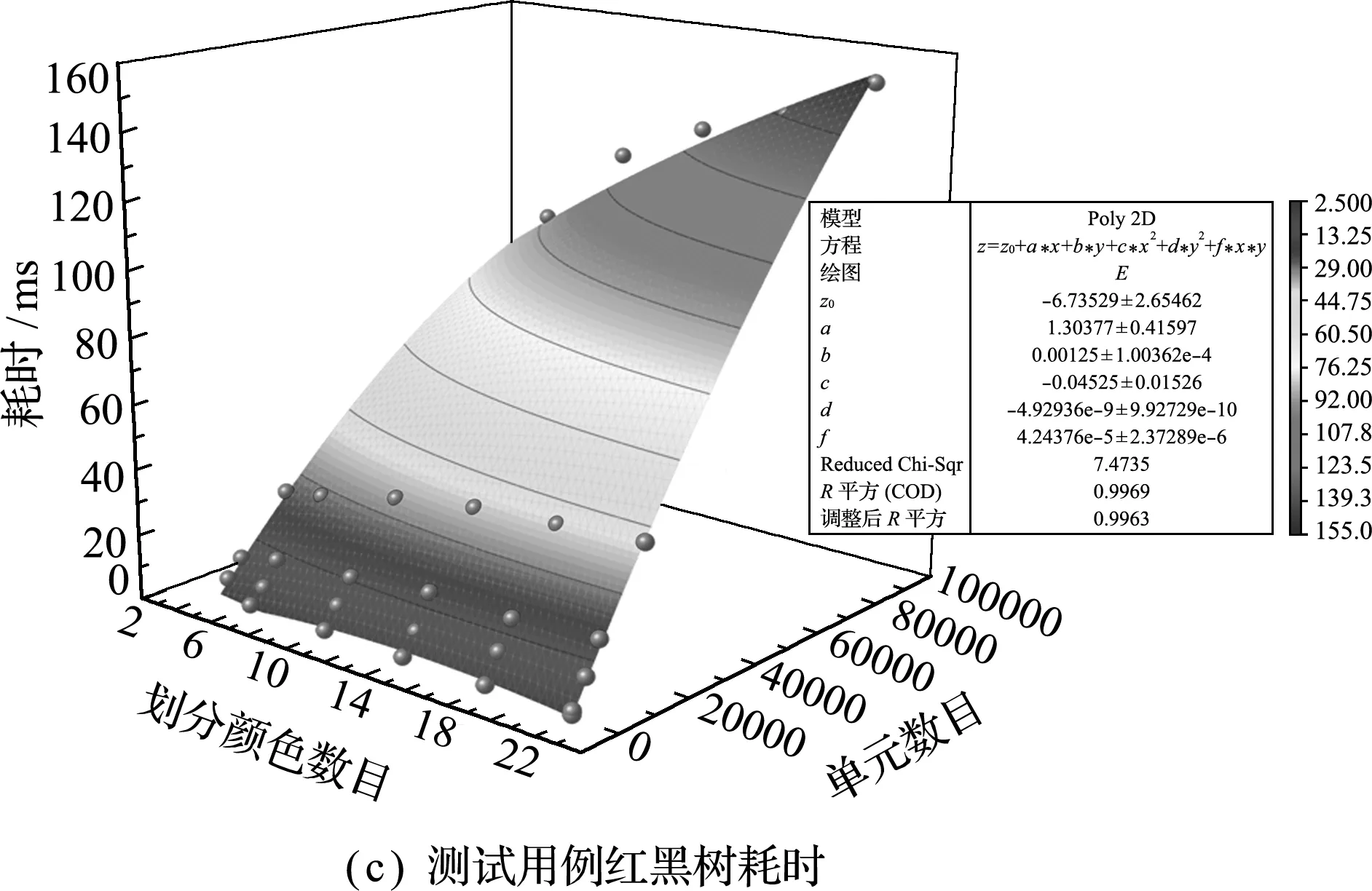
图7 各测试用例划分耗时

Fig.7 Time-consuming for partitioning test cases

为保证装配算法在常用的二次单元中同样有较好的通适性，选取表3的编号3模型和编号5模型，分别将各单元替换为二阶四边形-三角形壳元和二阶六面体等参单元。并行装配算法横向对比结果如图8所示。以双精度计算并调用cudaThreadSynchronize函数保证线程同步后截止计时，记录不包括主机-设备端传输耗时之外的所有耗时项。由于高阶单元需要更多的计算量、共享内存及寄存器空间，其耗时相应也较低阶单元更多；同时如图8(b)所示,在单元数较多时，基于共享内存的非零组装算法在二阶单元情况下获得了约3的加速比，单纯从组装算法耗时看能够满足至多 25 ms 步长的实时仿真要求，而颜色重排序算法仅获得了约2倍的加速效果，无法满足实时性要求。但是值得注意的是，图8两算例的耗时均在单台工作机上统计，而颜色分割重排序算法可将任务分配至计算集群内的多个计算节点同时组装，由于GPU组装相较于基于颜色划分的组装算法会产生额外的CPU-GPU内存拷贝操作，因此颜色重排序后将任务分配至各计算节点的策略在此情况下的计算耗时可能比共享内存的非零组装算法更少。

为进一步验证并行组装算法在单机多GPU节点的耗时情况，经修改主程序，以单元颜色分组后的单双号为识别，将单色号单元分配至GPU0内组装，双色号单元分配至GPU1内组装，获得如图9所示的结果。对比在计算平台1的计算耗时，颜色分割重排序算法没有发生明显的时间变化，其原因是在该算法中，METIS进行颜色分割的耗时占据了很大一部分，其作为在CPU上运行的串行算法并不能因新GPU的引入而实现性能提升，符合Amdahl定律。但基于共享内存和全局显存的非零组装算法均有一定的性能提升，尤其编号5的二阶单元组装算例中，因单元数较多能够启动足够多的核函数，基于共享内存的非零组装算法几乎呈线性加速，耗时控制在10 ms以内，实现了约6的加速比。

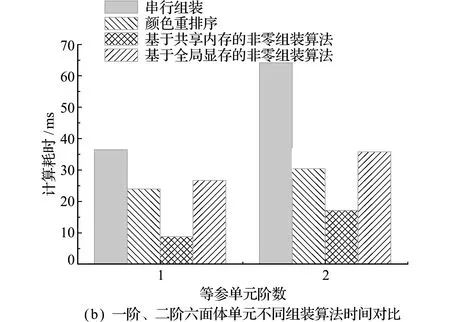
图8 一阶、二阶单元不同组装算法耗时对比

Fig.8 Time comparison of different assembly algorithms for first-order and second-order elements

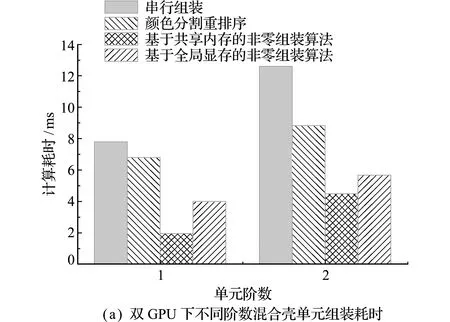
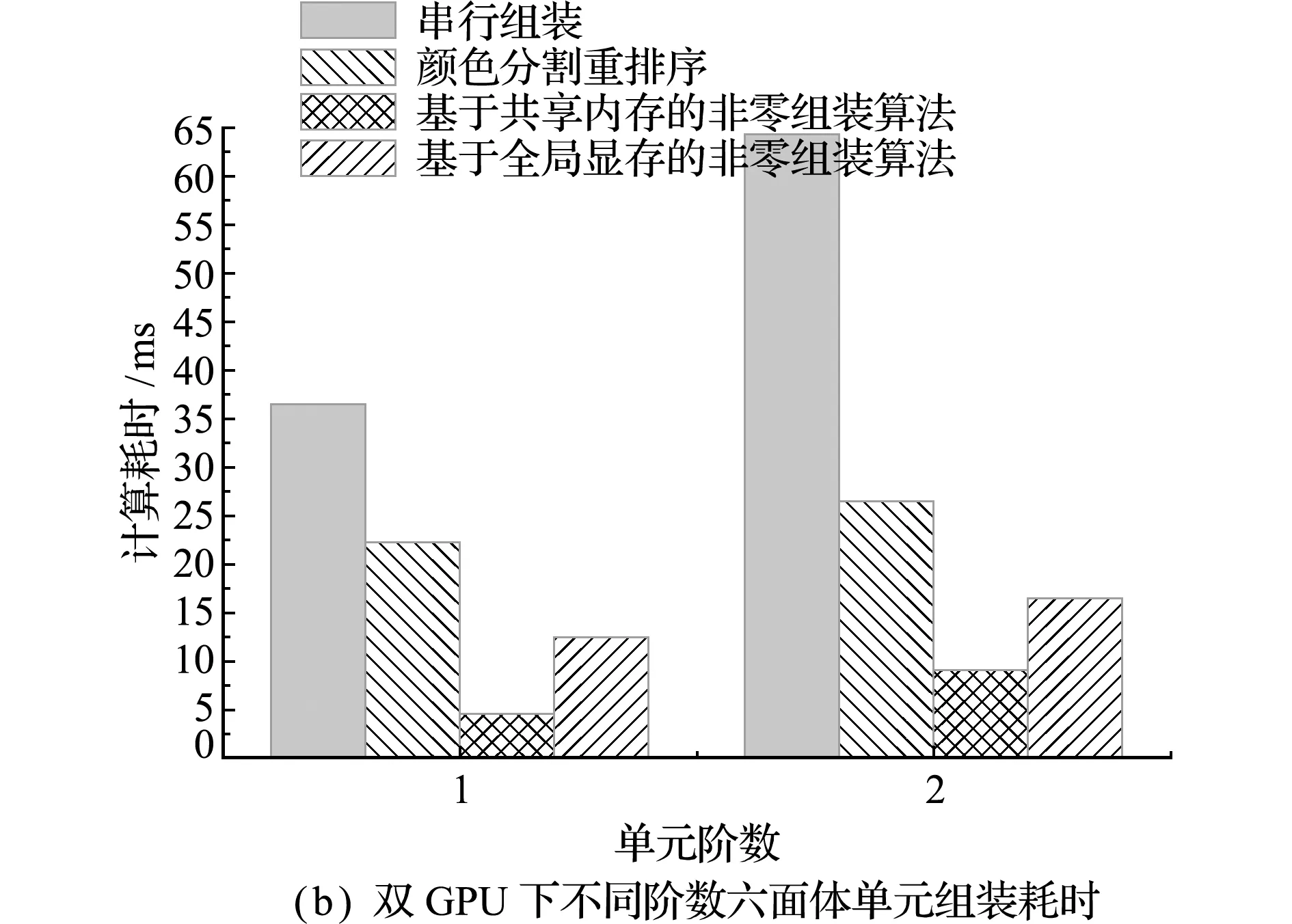
图9 双GPU下不同阶数单元组装耗时

Fig.9 Time-consuming comparison of different order unit assembly under dual GPU

4 结 论

为了设计适用于弹性飞行器飞行动力学仿真及结构快速故障诊断平台，作为初步的算法研究，设计了不同种类的有限元组装算法，以常用的着色算法为基础，提出了全局显存和共享内存的非零元素组装算法。以航天器典型部件为算例，提出了适宜于不同阶数单元的组装算法，在双精度下采用单机双GPU达到了约6倍的加速比，用以往25 ms的制导周期作为判据，二阶单元在20000余个时仍能通过共享内存的非零组装模式满足组装的实时性要求。但没有讨论单元矩阵存储模式对组装算法的影响，也未讨论单精度算法能够在满足精度的条件下允许更多的单元满足实时组装的需求。以上两点将是未来的研究重点。