水平荷载下型钢再生混凝土柱-钢梁组合框架受力性能非线性数值分析

马 辉，席嘉诚，黄 成，张 鹏，董 静

(西安理工大学 土木建筑工程学院，西安 710048)

1 引 言

近年来，我国城市化水平逐步提高，城区的拆迁和扩建项目的开展，不仅产生了大量的建筑垃圾，同时也需要大量的建筑砂石材料，因此，各国一直致力于建筑垃圾资源化的研究，以解决资源利用与建筑垃圾给人类带来的一系列问题。再生混凝土材料的研究和推广应用，旨在采用科学的管理手段来有效地消耗建筑垃圾，是一种从源头解决建筑垃圾问题的绿色方法，其有效地防止了资源浪费与环境破坏，提高了建筑垃圾回收利用率，推动经济持续发展，维护社会和谐稳定[1-5]。

文献[6]研究表明，限制再生混凝土工程应用的关键原因是其基本力学性能普遍劣于普通混凝土。为推广再生混凝土材料的应用范围，部分学者将其与钢材组合形成钢与再生混凝土的组合结构，如型钢再生混凝土组合柱，该柱不仅有高承载力和高延性的优点，而且还有效地利用了再生混凝土，具有绿色环保的显著特征，扩大了再生混凝土材料的应用范围，提高了建筑垃圾再利用效率。为进一步加强再生混凝土利用的理论基础，丰富数据内容，马辉等[7,8]在型钢再生混凝土柱的基础上，结合钢梁的力学性能优势，提出了型钢再生混凝土柱-钢梁组合框架结构，对该组合框架节点的受力性能、破坏机理以及抗剪承载力计算方法等进行了研究，结果表明，该组合框架节点具有承载力较高和抗震性能较好等优点。然而，目前对型钢再生混凝土柱-钢梁组合框架结构受力性能的研究很少，尤其对该组合框架受力性能非线性有限元分析尚未见报道，因此，有必要对此展开相关研究。

本文结合型钢再生混凝土柱-钢梁组合框架拟静力试验，采用合理的材料本构关系和非线性理论，通过数值分析软件Abaqus建立型钢再生混凝土柱-钢梁组合框架数值模型，获取该组合框架的变形特征、应力云图及荷载-位移骨架曲线等，对数值分析计算值和实验值进行对比，验证了有限元模型的合理性。在此基础上，为进一步完善该组合框架的非线性受力行为的理论研究，对该组合框架的受力性能进行数值参数扩展分析，研究结论可为该组合框架的研究应用提供依据。

2 组合框架拟静力试验概况

2.1 试件设计与制作

试验制作了一榀两跨三层，缩尺比为1∶2.5实腹式配钢的型钢再生混凝土柱-钢梁组合框架试件。该组合框架试件底层、中间层及顶层的层高分别为1.8 m,1.5 m和1.5 m，柱间距为2.4 m，组合框架如图1所示，组合框架具体构造数值及有关横截面配筋如图2所示。再生粗骨料来源于建筑垃圾的废弃混凝土，采用颚式破碎机将废弃混凝土破碎后形成。再生混凝土材料的再生粗骨料取代率为100%，按C40再生混凝土强度设计，水灰比为0.466，配合比为水∶水泥∶砂子∶粗骨料=206.7∶443∶576∶1171；再生混凝土的基本力学性能为fc u=51.88 MPa,fc=39.43 MPa,ft k=12.45 MPa和E=2.799×104MPa。钢材的基本力学性能指标列入表1。

2.2 加载制度和测点布置

型钢再生混凝土柱-钢梁组合框架的边柱和中柱轴压比分别为0.2和0.4，竖向恒定荷载由油压千斤通过分配梁施加至柱顶，水平荷载在顶层中心轴处施加。试验首先通过调节荷载等级差值进行逐级加载，以20 kN为荷载等级差值，每级加载循环反复1次；当再生混凝土出现裂缝后，调整荷载等级差值为40 kN进行循环反复1次；试件达到屈服以后，采用位移调节加载制度，按屈服位移的 1.5 倍进行循环反复加载，每级循环反复加载3次，当水平荷载降到峰值荷载的85%时结束试验。图3为该组合框架的拟静力加载设备和水平荷载作用的加载制度。试件的主要测点如下,在组合框架每层梁的中心线位置处布置一个位移计，以量测框架的层间侧移大小；在型钢再生混凝土柱根部及节点区附近的型钢、纵筋和箍筋上布置应变片，型钢梁的应变片主要布置在梁端区域，以量测组合框架关键部分的应变发展规律。

表1 钢材的基本力学性能指标

Tab.1 Mechanical performance indexes of steel products

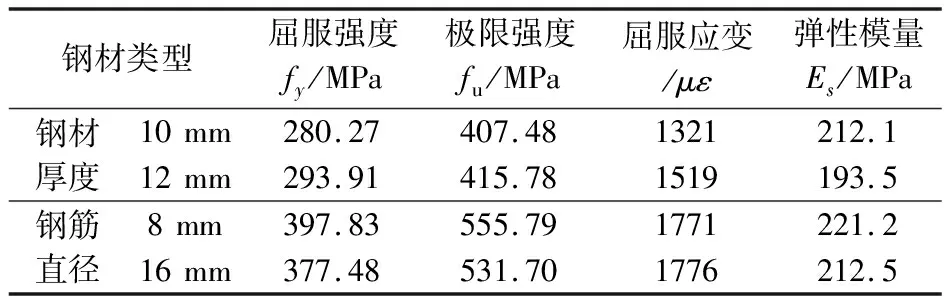
钢材类型屈服强度fy/MPa极限强度fu/MPa屈服应变/με弹性模量Es/MPa钢材厚度10mm280.27407.481321212.112mm293.91415.781519193.5钢筋直径8mm397.83555.791771221.216mm377.48531.701776212.5

图1 组合框架试件设计与加载现场(单位：mm)

Fig.1 Design of composite frame specimens and test loading device(unit:mm)

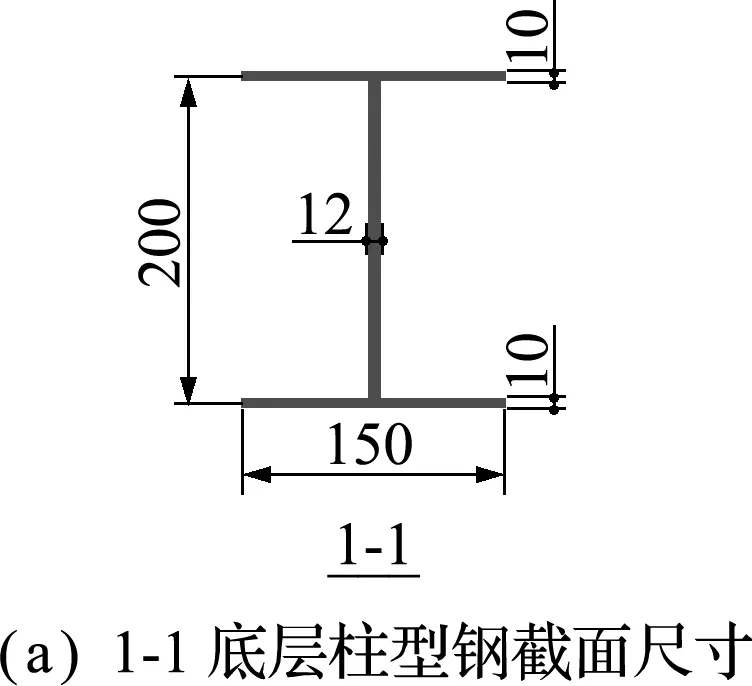
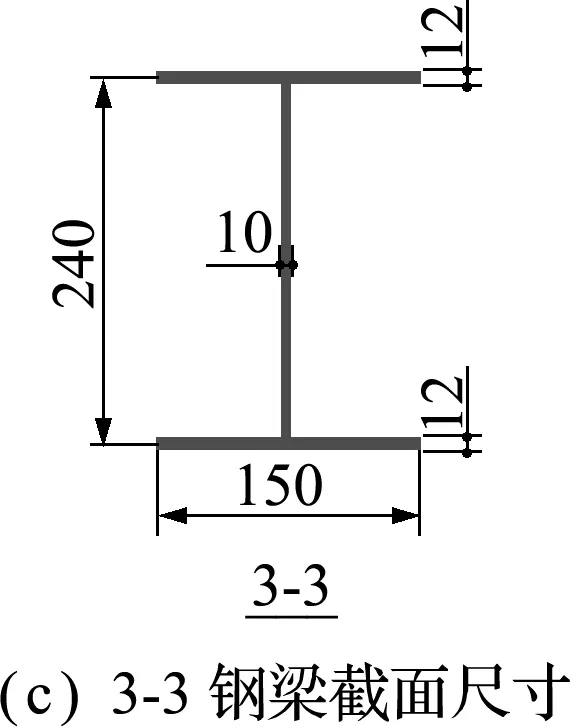
图2 钢梁截面尺寸和型钢再生混凝土柱配筋(单位：mm)

Fig.2 Section size of steel beam and reinforcement of profile steel reinforced recycled concrete column(unit:mm)

图3 组合框架加载设备与水平荷载加载制度

Fig.3 Loading equipment of composite frame and loading system of horizontal load

3 型钢再生混凝土柱-钢梁组合框架数值分析模型的建立

3.1 再生混凝土材料本构关系

在型钢再生混凝土柱-钢梁组合框架拟静力试验过程中，组合框架的型钢再生混凝土柱在水平荷载作用下存在受压区和受拉区，因此本文有限元模型中再生混凝土材料需要分别考虑受压和受拉本构关系。

3.1.1 再生混凝土受压应力-应变关系

目前，关于再生混凝土单轴受压应力-应变曲线本构关系的研究相对较多，其中肖建庄教授对再生混凝土材料本构关系的研究较为系统，建立了以再生粗骨料取代率为变化参数的单轴受压本构关系。为便于计算，本文在进行有限元模拟时采用文献[8]提出的再生混凝土单轴受压本构关系，其数学方程表达式为

(1)

式中x=ε/ε0，y=σ/fc，ε0为峰值应变，ε0=1.998×10-3，fc为轴心抗压强度；a为再生混凝土的初始弹性模量，即表示曲线初始斜率的大小，随着再生粗骨料取代率的增加而减小；b值随着再生粗骨料取代率的增加而增大，越大则表示再生混凝土延性越差；参数a和b的计算见式(2)，其中r为再生粗骨料取代率。

a=2.2(0.748r2-1.23r+0.975)

b=0.8(7.6483r+1.142)

(2)

本文试验中，型钢再生混凝土柱-钢梁组合框架的再生粗骨料取代率为100%，因此通过式(2)可计算得出a和b取值分别为1.04和7.5。

3.1.2 再生混凝土受拉应力-应变关系

由于再生混凝土属于脆性材料，大多数学者只研究了再生混凝土单轴受拉本构关系的上升段，而对于再生混凝土单轴受拉本构关系的下降段却少有报道，这主要是由于脆性材料在拉伸作用下变形一般为小变形，其受拉应变不易测出，导致再生混凝土材料的直接拉伸试验操作较为困难，对试验设备和技术要求比较高[9]。文献[10,11]在进行再生混凝土构件或结构数值分析时，再生混凝土受拉本构表达式采用肖建庄教授提出的曲线上升段[12]，并借鉴规范[13]中普通混凝土材料的受拉本构关系的下降段，构成了再生混凝土材料受拉本构关系全过程曲线，取得了较好的非线性模拟效果。因此，本文所使用的再生混凝土材料单轴受拉本构关系表达式为

(3)

再生混凝土材料的强度准则采用Drucker-Prager强度准则，同时材料损伤因子的取值参考文献[12]。

3.2 钢材本构关系

该组合框架采用的钢材为碳素钢，假定服从Von Mises屈服准则，可采用四折线弹塑性本构关系曲线，其表达式为

(4)

式中Es和Ek分别为钢材弹性阶段和强化阶段的弹性模量，Ek=0.01Es；fy和εy分别为钢材达到屈服时的应力和应变，fu和εu分别为钢材达到极限时的应力和应变，相关参数取值可参考表1。

3.3 单元类型及网格划分

型钢梁、内置型钢柱以及再生混凝土均采用C3D8R单元类型，柱中纵筋和箍筋则使用T3D2单元类型[14]，建立组合框架数值分析模型。图4(a～c)为型钢再生混凝土柱-钢梁组合框架试件的各部分网格划分示意图，单元尺寸均为50 mm。

3.4 材料相互作用与加载设置

现有研究表明，再生混凝土和型钢之间粘结滑移的影响较小[15,16]，因此在建立模型时，本文认为型钢、钢筋和再生混凝土三者协同工作，接触采用embed嵌入式。基础梁与地面刚性连接，两个边柱和中柱的柱顶部设置耦合约束，顶层梁端远离一定距离设置耦合点，图4(d)为组合框架耦合点布置图。本次有限元计算模拟设置两个分析步加载，首先，通过参考耦合点在每个柱顶部施加竖向固定荷载；其次，在梁端部的耦合点施加相应的水平荷载，通过试验研究确定荷载控制量。

4 有限元计算结果分析

4.1 组合框架变形图与应力云图

图5为组合框架的数值模型和试验变形图。从图5(a)的有限元模型计算结果可以看出，在柱脚以及钢梁梁端位置变形较大，柱脚部位受P-Δ效应的影响发生变形，节点区域附近钢梁形成塑性铰，与试验破坏部位发生在型钢再生混凝土柱脚以及钢梁梁端位置基本一致，表明数值分析模型受力特征与试验破坏形态类似。

4.1.1 再生混凝土等效塑性应变云图

图6分别为组合框架不同荷载阶段下，再生混凝土的等效塑性应变云图分布。随着水平荷载的增加，组合框架达到屈服荷载时，中柱底层和中层节点域的再生混凝土出现了部分塑性变形；组合框架达到峰值荷载时，中柱的底层和中层节点域钢梁梁端与型钢再生混凝土柱相交位置处，再生混凝土的应力相对集中，这是因为组合框架在受水平推力的作用下，钢框架节点区域附件发生了应力集中，使得节点区域及钢梁上下部分的再生混凝土受挤压，从而应力相对较大；在水平推力作用下，柱脚部位的右侧再生混凝土受压而出现较大的塑性变形；组合框架达到极限荷载时，在水平推力作用下柱子发生了明显的侧向弯曲，使得型钢再生混凝土柱底部与基础梁连接部位产生了较大范围的塑性变形，框架柱的脚柱均出现了不同程度的塑性变形，中柱柱脚的右侧塑性变形最为明显，这是由框架在水平推力和中柱承受的最大轴压力共同作用下形成的。

4.1.2 钢材应力云图

图7为组合框架不同荷载阶段下型钢框架的应力分布。组合框架达到屈服荷载时，中柱中层节点梁端型钢上翼缘局部应力为309.3 MPa，开始进入屈服阶段，同时其余各层节点的梁端翼缘处也均出现不同程度应力集中；另外左柱脚型钢翼缘因受拉而产生了局部弯曲，并未屈服，但产生了相对较大的应力，这是因为组合框架在P-Δ效应的影响下，各层钢梁端部处上下翼缘受到了挤压变形而产生了应力集中；组合框架达到峰值荷载时，梁端上下翼缘型钢应力为321.1 MPa，中柱中层节点域梁端型钢翼缘及腹板局部已经处于屈服状态，中柱底层和中层的型钢再生混凝土柱的型钢翼缘局部应力较大但未屈服，同时各柱脚型钢翼缘均达到不同程度的屈服，其中以左柱脚端翼缘受拉侧屈服面积最大；当达到极限荷载时，中柱中层梁端型钢应力为359.8 MPa，各梁端翼缘及腹板已经完全屈服，中柱的底层和中层的型钢再生混凝土柱的型钢翼缘局部屈服，柱脚部位型钢腹板也基本屈服，其中左柱脚腹板屈服面积最大。

图4 组合框架网格划分和与耦合点设置

Fig.4 Mesh generation and coupling point setting of composite frame

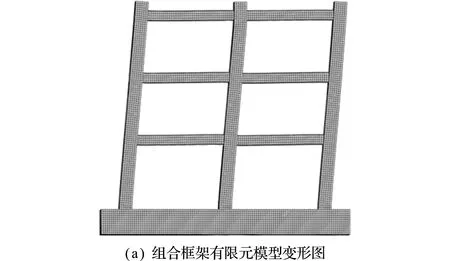
图5 组合框架变形特征

Fig.5 Deformation characteristics of composite frame

另外，因再生混凝土的塑性变形作用，中柱各节点域附近的钢筋骨架应力相对较大，这是因为在水平推力和轴压力共同作用下，钢梁端部发生了较大的塑性变形和柱脚型钢变形导致的。

由上可知，在加载过程中，组合框架整个破坏全过程表现为柱脚部位再生混凝土先开裂；随后，型钢梁端部翼缘和腹板先后屈服，形成塑性铰；最后，型钢再生混凝土柱中柱脚型钢翼缘和腹板先后屈服形成塑性铰域，导致组合框架的承载力降低。该组合框架的整体破坏过程和顺序总体符合强柱弱梁和强节点弱构件的破坏机制。

4.2 计算骨架曲线

图8为组合框架整体及各层间的荷载-位移数值分析结果曲线与试验结果曲线对比，其中FEM代表数值分析结果曲线，TEST代表试验结果曲线。表2为组合框架的各特征值及误差对比。从图8和表2可知，组合框架数值分析结果与试验结果较为接近，且数值分析结果与试验结果曲线趋势规律性基本相似，组合框架荷载-位移骨架曲线可分为弹性阶段、屈服阶段、强化阶段及下降段。加载初期，曲线基本呈线性增长关系，组合框架近似处于弹性阶段，曲线较陡，表明组合框架初始刚度较大；随着荷载的增加，骨架曲线逐渐偏向横坐标轴，即曲线斜率减小，组合框架进入弹塑性阶段；峰值荷载过后，骨架曲线呈现缓慢下降的趋势，说明组合框架在后期依然具有良好的承载力和延性。总体上，组合框架有限元计算骨架曲线的刚度和峰值承载力均大于试验结果，两者峰值荷载相差9.6%，造成的原因可能有，(1)组合框架数值分析计算时采用的再生混凝土受拉本构与实际情况存在差异；(2)型钢嵌固于再生混凝土中，属于刚性约束关系，未考虑型钢与再生混凝土之间粘结滑移的影响；(3)试验研究中组合框架在不断循环往复的过程中逐渐积累损伤，而有限元分析采用单向水平推力加载，两者存在一定差别。

5 有限元参数分析

在上述数值计算分析结果的基础上，对组合框架数值模型进行扩展参数分析，深入分析不同参数的变化对组合框架受力性能及非线性行为的影响，主要考虑再生混凝土强度等级、梁柱线刚度比、轴压比和型钢强度等设计参数。图9和图10分别为不同设计参数对组合框架整体骨架曲线的影响规律和不同设计参数对组合框架水平承载力的影响规律。

图6 再生混凝土等效塑性应变分布

Fig.6 Equivalent plastic strain distribution of recycled concrete

图7 钢框架的应力分布

Fig.7 Stress distribution of steel frame

(1)再生混凝土强度等级

从图9(a)和图10(a)可以看出，不同再生混凝土强度等级的荷载-位移骨架曲线变化趋势较为相似，没有出现曲线突变；从骨架曲线的初始斜率和水平承载力的变化趋势可知，再生混凝土强度等级从C40到C60时，该组合框架的初始刚度和峰值承载力也随之提高，组合框架的峰值承载力增幅为7.5%，但组合框架的变形能力随着再生混凝土强度的升高逐渐降低，即提高再生混凝土强度对组合框架的抗震延性是不利的。

(2)型钢强度

如图9(b)所示，内置不同强度型钢的组合框架骨架曲线斜率差异明显，型钢强度越高，框架的初始刚度越大；组合框架进入弹塑性阶段时,骨架曲线走势差异更加明显，框架的水平承载力随着型钢强度的提高而明显提高。图10(b)为型钢强度对组合框架水平承载力的影响，型钢强度由Q235提高至Q345，组合框架的水平承载力提高了6.62%，由Q235提高至Q390，组合框架的水平承载力提高了21.54%，由此得知，提升内置型钢的材料强度可有效提高组合框架的水平承载力。

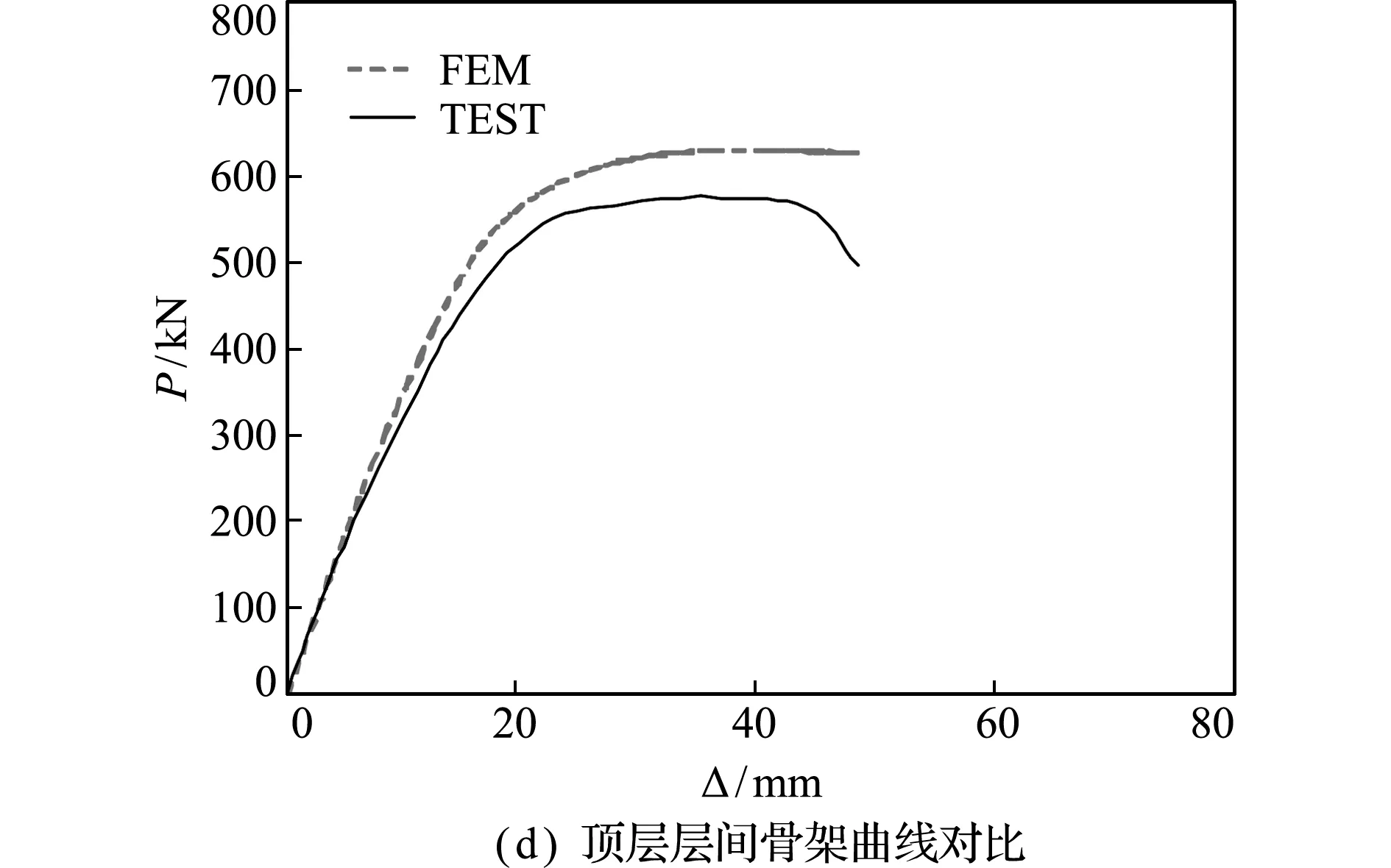
图8 试验曲线与有限元计算骨架曲线对比

Fig.8 Comparisons between experimental curves and finite element skeleton curves

表2 组合框架数值模拟值与试验值的特征值对比

(3)轴压比

从图9(c)可以看出，随着轴压比的增大，组合框架的水平承载力逐渐降低；达到峰值荷载后，轴压比越大，组合水平承载力降低速率越大，表明组合框架的抗震延性随着轴压比的增大而逐渐降低；由此可见，轴压比对组合框架水平承载力具有一定的影响，因此为保证组合框架的变形能力，需要对轴压比进行控制，根据文献[17]的相关研究，组合框架轴压比限值建议取为n≤ 0.65。

图9 主要设计参数对组合框架整体骨架曲线的影响规律

Fig.9 Influences of main design parameters on skeleton curves of composite frames

图10 主要设计参数对组合框架水平承载力的影响

Fig.10 Influences of main design parameters on horizontal bearing capacity of composite frames

(4)梁柱线刚度比

从图9(d)可以看出，加载前期，组合框架骨架曲线的位移变化随着荷载呈正比例增长，不同梁柱线刚度比的组合框架初始刚度具有明显差异；梁柱线刚度比的增大使得组合框架的初始斜率即初始刚度也随之增大；弹塑性阶段后，组合框架骨架曲线呈非线性变化，荷载-位移骨架曲线差异越为明显。从图10(d)可以看出，梁柱线刚度比从 0.1683 提高至0.3637，组合框架模型的峰值承载力提高了11.8%。另外，不同梁柱线刚度比的组合框架层间位移角基本相当，故梁柱线刚度比对该组合框架整体的刚度和承载力影响较大，而对其延性的影响相对较小。

6 结 论

(1)在水平荷载下，组合框架柱脚部位再生混凝土先发生开裂；随后，型钢梁端部上下翼缘和腹板先后发生屈服，形成塑性铰；最后，型钢再生混凝土柱中柱柱脚型钢翼缘和腹板先后屈服，导致组合框架的承载力降低。该组合框架符合强柱弱梁和强节点弱构件的破坏机制。

(2)组合框架数值分析计算模型的计算值与试验值误差较小，峰值荷载误差为9.6%，计算曲线与试验曲线趋势基本一致，表明数值分析计算模型能较好地模拟该组合框架在水平荷载下的非线性受力行为。

(3)提高再生混凝土强度等级，组合框架的承载力和刚度也随之提高，水平承载力最大增幅为7.5%，而且不利于组合框架的变形；组合框架的承载力和刚度明显随型钢强度的提高而提高，峰值荷载最大可提高21.5%。

(4)增大轴压比会降低组合框架的承载力，峰值荷载最大降低7.9%，同时也会降低组合框架的变形能力；梁柱线刚度比的提高会增大组合框架的承载力，也会增大组合框架的刚度，峰值荷载最大提高11.8%。