单箱双室组合箱形梁桥静力学特性的研究

王根会，陈义勤，樊 江，甘亚南

(1.兰州交通大学 土木工程学院,兰州 730070; 2.上海华东铁路建设监理有限公司,上海 200070; 3.甘肃省交通规划勘察设计院股份有限公司,兰州 730070; 4.盐城工学院 土木工程学院,盐城 224051)

1 引 言

波纹钢腹板组合箱梁是20世纪末出现的一种新型组合结构，由于其自重轻，预应力效率高，而且有效解决了温度应力、收缩和徐变等因素带来的桥梁病害，因而该类结构具有良好的力学性能[1-3]。自从1986年法国建成世界上第一座波纹钢腹板组合箱梁桥—Cognac桥，世界上已建波纹钢腹板组合箱梁桥已达400余座，如日本的矢作川桥为单箱五室组合曲线箱形梁桥。现阶段，我国该类桥梁已有70余座，如青海三道河桥即为单箱双室组合箱梁桥。并且随着桥面宽度的增加，单箱多室组合箱形梁桥拥有更为广阔的发展前景，因而其力学性能的研究更具理论和工程实际意义[4,5]。实际上，组合箱形梁桥为竖向弯曲状态，由于波纹钢腹板的褶皱效应，其腹板仅承受剪力，而翼板将同时承受轴力和弯矩，因而其良好的力学性能避免了很多结构病害[5,6]。尽管学者们对组合箱梁进行过很多的理论探索和试验研究，但是该类结构力学分析中，依然存在诸多缺陷[7,8]，既有文献均未同时考虑剪滞翘曲应力自平衡、腹板褶皱效应和铁木辛柯剪切变形等因素。

基于此，本文以最小势能原理为基础建立了组合箱梁的弹性控制微分方程和自然边界条件，算例分析了剪力滞后和褶皱效应等因素对该类结构力学性能的影响[9,10]。因而，本文理论为组合箱梁力学性能的精细化分析提供了新方法，且对该类结构设计具有一定的指导作用。

2 单箱双室组合箱梁的控制微分方程及自然边界条件

2.1 波纹钢腹板剪切模量的修正

根据文献[6,9]研究成果，波纹钢腹板剪切模量的大小与其波纹几何形状有关,如图1所示，因而波纹钢腹板剪切模量Gs的修正公式为

(1)

式中Es和υs为波纹钢腹板材料的弹性模量和泊松比，L1,L2和L3分别为波纹钢腹板平板段长度、斜板段长度以及斜板段在水平面内投影。

2.2 组合箱梁翼板纵向翘曲位移函数的设置

图2所示为单箱双室波纹钢腹板组合箱梁，若箱形结构的跨度为L，对称弯曲状态w(z)和θ(z)为初等梁理论组合箱梁的竖向挠度和截面竖向转角，f1(z)，f2(z)和f3(z)为悬臂板和上下翼板剪力滞效应引起结构的竖向挠度。悬臂板和上下翼板纵向位移u1,u2和u3则为初等梁理论值、剪力滞效应引起箱梁翼板的翘曲位移，以及箱梁翼板间剪滞效应相互作用之和，可表示为[11]

图1 波形钢腹板的几何形状

Fig.1 Geometric shape of corrugated steel webs

悬臂板纵向位移

u1(λ,y,z)=yθ+[y-α1Ψ1(λ)-β1]f′1+

(y-β2)f′2+(y-β3)f′3

(2)

式中Ψ1(λ)=cos[(πλ/(2b1)]为组合箱梁悬臂翼板不均匀分布函数，α1和β1为悬臂板满足剪滞翘曲应力自平衡的修正系数。其中0≤λ≤b1。

悬臂翼板剪滞翘曲应力

σx B=E[y-α1Ψ1(λ)]f″1-Eβ1f″1

(3)

上翼板纵向位移

u2(λ,y,z)=yθ+[y-α2Ψ2(λ)-β2]f′2+

(y-β1)f′1+(y-β3)f′3

(4)

式中Ψ2(λ)=cos[(πλ)/(2b2)]为箱梁上翼板的不均匀分布函数，α2和β2为上翼板满足剪滞翘曲应力自平衡的修正系数。其中0≤λ≤b2。

上翼板剪滞翘曲应力

σS Y=E[y-α2Ψ2(λ)]f″2-Eβ2f″2

(5)

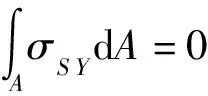
下翼板纵向位移

u3(λ,y,z)=yθ+[y-α3Ψ2(λ)-β3]f′3+

(y-β1)f′1+(y-β2)f′2

(6)

式中α3和β3为下翼板满足剪滞翘曲应力自平衡的修正系数。其中0≤λ≤b2。

下翼板剪滞翘曲应力

σX Y=E[y-α3Ψ2(λ)]f″3-Eβ3f″3

(7)

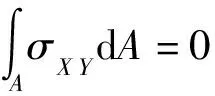
将悬臂翼板、上翼板和下翼板作为独立的力学体系，其将各自满足剪滞翘曲应力的自平衡。

图2 波纹钢腹板组合箱梁截面

Fig.2 Cross section of box girders with corrugated steel webs

2.3 组合箱梁体系的总势能

(1)箱形梁悬臂板和上下翼板总应力

悬臂翼板

σZ B=Eyθ′+E(y-α1Ψ1)f″1-Eβ1f″1+

E(y-β2)f″2+E(y-β3)f″3

(8)

(9)

上翼板

σZ S=Eyθ′+E(y-α2Ψ2)f″2-Eβ2f″2+

E(y-β1)f″1+E(y-β3)f″3

(10)

(11)

下翼板

σZ X=Eyθ′+E(y-α3Ψ2)f″3-Eβ3f″3+

E(y-β1)f″1+E(y-β2)f″2

(12)

(13)

(2)组合箱梁悬臂板以及上下翼板变形势能

(14)

其中，箱梁悬臂板和上下翼板各自变形势能为

(15)

(16)

(17)

分析可得

式中A1为悬臂板面积，A2为上翼板面积，A3为下翼板面积，且

A=A1+A2+A3

I4=0,I5=0,I6=0

最后，可得

(18)

波纹钢腹板剪切应变能

(19)

结构体系荷载势能

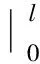
[M1(z)f′1(z)+M2(z)f′2(z)+

(20)

则系统总势能

U=UZ 1+Up+TZ j

(21)

式中M1(z),M2(z)和M3(z)为组合箱梁悬臂板及上下翼板剪滞效应产生的关于x轴弯矩，Mz(z)为梁段端产生竖向转角θ(z)时关于x轴的弯矩，Q(z)和qy(z)为梁段端竖向剪力及箱形梁上竖向分布力，E和G为箱梁顶底板材料的杨氏弹性模量和剪切弹性模量，As为波纹钢腹板截面积之和。

2.4 单箱双室组合箱梁控制微分方程及边界条件

根据变分原理δU=0，可推导出组合箱梁的微分方程和自然边界条件。

EIθ″+GsAs(w′-θ)=0

(22)

GsAs(w″-θ′)+qy=0

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

由微分方程组可得,单箱双室组合箱梁由2个独立的力学体系组成，即由初等梁理论和剪滞理论体系叠加而成。

2.5 组合箱梁控制微分方程的求解

将微分方程(22,23)整理代换，可得w(z)和θ(z)的方程。

(35)

(36)

式中c1,c2,c3和c4为方程w(z)和θ(z)的常系数，可根据相应边界条件获得。

由微分方程(25，26)，可得

(37)

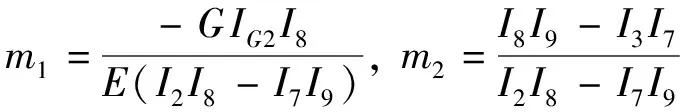
由微分方程(24，26)，可得

(38)

将方程(37，38)整理代换，可得

(39)

对于方程(39)，其特征方程解为

r1,2=±η1，r3,4=±η2，r5,6=±η3

方程f3(z)的解为

f3(z)=e1chη1z+e2shη1z+e3chη2z+

e4shη2z+e5chη3z+e6shη3z+e7z+

(40)

基于方程f3(z)，假设f1(z)和f2(z)为方程解形式，将其代入微分方程组(24，25)求得f1(z)和f2(z)的常系数，可得f2(z)和f1(z)方程为

f2(z)=e1D1chη1z+e2D1shη1z+e3D3chη2z+

e4D3shη2z+e5D5chη3z+e6D5shη3z+

(41)

f1(z)=e1B1chη1z+e2B1shη1z+e3B3chη2z+

e4B3shη2z+e5B5chη3z+e6B5shη3z+

(42)

其中

式中e1,…，e12为方程f1(z),f2(z)和f3(z)的常系数，同样可根据相应边界条件求得。

3 单箱双室组合箱梁常用边界条件

根据边界条件(27，28)，可得初等梁理论具体边界条件。

相关w(z)和θ(z)的边界条件

(1)均布荷载

(43)

(2)集中荷载

对于简支组合箱梁，跨间受力为一个或多个集中力，如图3所示，且集中力Pk距左右相邻边界距离为Lk 1和Lk 2，若w(z)和θ(z)的下标代表其处于z1或z2坐标系，则k点需引入下列连续边界条件。

(44)

同样，根据方程(29～34)，可得相关f1(z)，f2(z)和f3(z)具体边界条件。如简支均布荷载为

(45)

4 单箱双室组合箱梁算例及分析

对于组合箱形梁桥，波纹钢腹板采用优质Q235型钢材，弹性模量为206 GPa，泊松比为 0.26，且波纹钢腹板厚度为tw=1.2 cm，箱梁高度为h=2.5 m，其顶板和底板均采用C50混凝土，厚度为t1=t2=t3=0.25 m，翼板长度b1=1.5 m,b2=2.5 m。如图1所示，L1=L2=43 cm，L3=37 cm，波纹钢腹板与上下翼板两端采用埋入式连接键连接。静力分析中均布力qy(z)=3×9800 N/m，集中力Pk(z)=3L×9800 N，其中L为组合箱梁跨度。(注：有限元分析中，采用ANSYS软件建立组合箱梁的空间有限元模型，顶底板均采用实体单元Solid65模拟，横隔板则采用Solid45模拟，而波纹钢腹板采用Shell63单元模拟，并且顶板和底板与波纹钢腹板采用共用节点连接方式。)

图3 组合箱梁坐标及荷载系统

Fig.3 Coordinate and load system of composite box girders

分析结果列入表1～表3和图4。可以看出，

(1)褶皱效应对组合箱梁翼板力学性能具有一定影响，且其对下翼板的作用大于上翼板，并且集中荷载组合箱梁褶皱效应的影响更为显著，如本文算例集中荷载下，上翼板与腹板交接处为 5.44%，而下翼板与腹板交接处为10.21%。

(2)组合箱梁剪滞效应更为突出，如算例中集中荷载底板和腹板相交处剪滞系数为1.48。相同条件下，集中荷载大于均布荷载剪滞效应，且随着跨宽比增大，其剪滞效应的影响逐渐减小。

(3)与组合箱梁传统分析理论相比较，本文方法计算精度明显提高。特别是集中荷载下对其上翼板的力学分析发现，翼板和腹板相交处两种算法影响率为-10.14%。

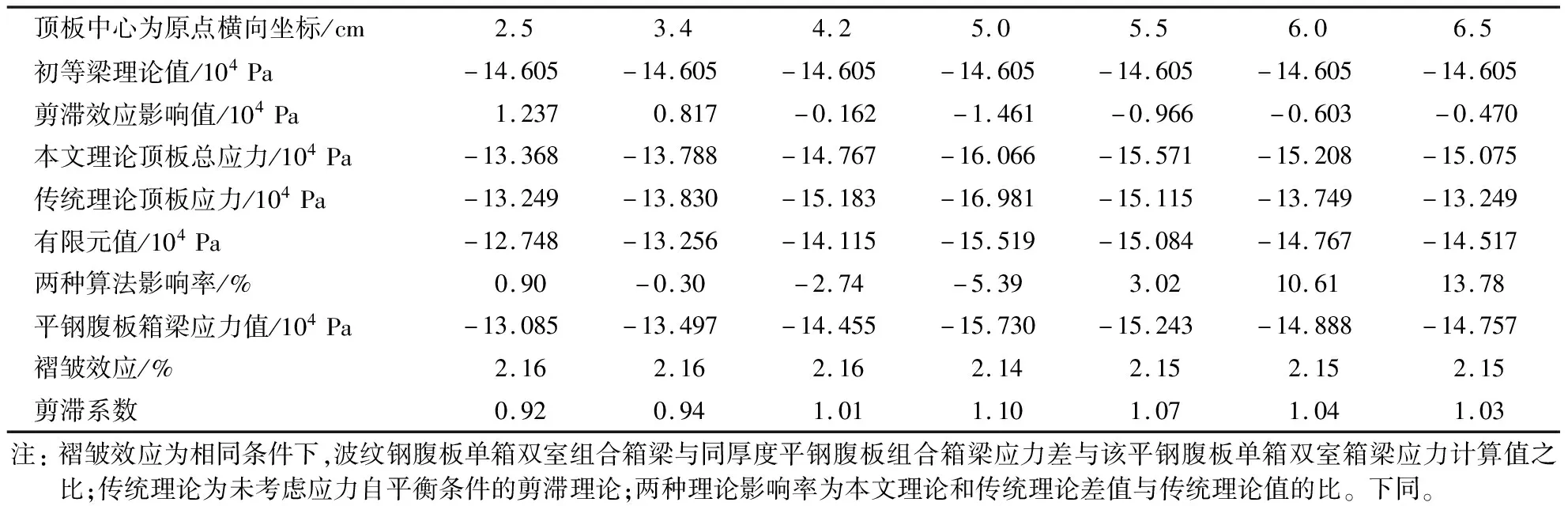
表1 简支组合箱梁顶板力学性能分析(z =L/2,L =18 m)(均布荷载)

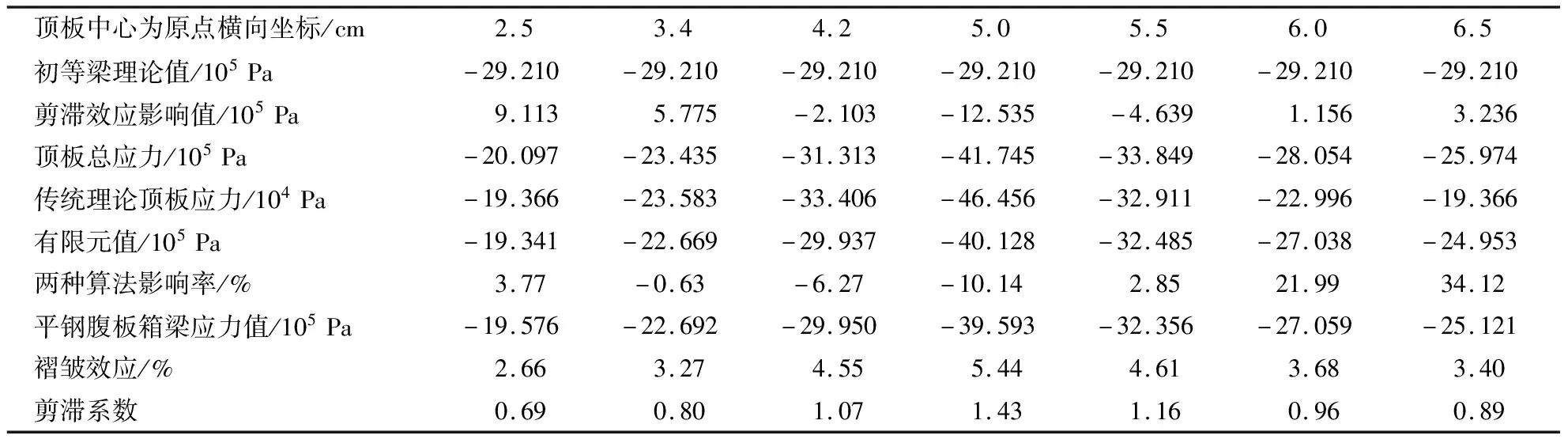
表2 简支组合箱梁顶板力学性能分析(L1=9 m,L2=9 m)(集中荷载)

表3 简支组合箱梁下翼板力学性能分析(L1=9 m,L2=9 m)(集中荷载)

图4 简支组合箱梁剪滞系数对比

Fig.4 Comparison of the shear lag coefficients for simply supported composite box girders

(4)由于剪滞翘曲应力自平衡条件的引入，组合箱梁力学性能分解为独立的初等梁理论和剪力滞理论体系，且翼板应力为两者的叠加值，这正是本文理论的创新点。

5 结 论

本文方法综合考虑了腹板褶皱效应、铁木辛柯剪切变形以及剪滞翘曲应力自平衡条件等因素，因而本文理论更具普遍意义。尽管波纹钢腹板褶皱效应影响下，单箱双室组合箱梁翼板压应力和拉应力皆有所增加，即组合箱梁竖向刚度降低，但是，由于波纹钢腹板褶皱效应影响，组合箱梁有效解决了温度应力、收缩和徐变等因素带来的桥梁病害。因而，本文方法更具理论和工程实际意义，且对该类结构耐久性设计具有一定的指导作用。