同径异速蛇形轧制弯曲曲率建模分析与研究
2020-06-29黄金博甄涛卫垚宇江连运
黄金博,甄涛,卫垚宇,江连运
(太原科技大学 机械工程学院,山西 太原 030024)
0 前言
制造业是国民经济的主体,是立国之本、兴国之器、强国之基。高强宽厚板广泛用于建筑工程、机械制造、船舶、核电、海上平台和压力容器等高端装备领域,是一种非常重要的结构材料[1]。高强、特厚钢板存在着由心部变形不充分而导致心部力学性能偏低的问题,为改善心部力学性能,一般采用提高总压缩比的方式来提高心部变形[2]。但受轧机能力和坯料尺寸的限制,压缩比难以达到要求而出现心部变形不充分、内部裂纹无法愈合和组织性能不均匀的问题,已经成为提高厚板质量的关键技术瓶颈。蛇形轧制综合了异步轧制的强变形渗透作用以及板形调控能力[3],为解决厚板心部变形不充分的问题指明了方向。
在非对称轧制过程中,变形区域内存在较高的剪应力,有利于使变形渗入中心部位,改善中心变形。M.Wroński[4]研究了非对称轧制钛的微观结构、晶体结构和残余应力,结果表明非对称轧制细化了金属的微观织构。A. Pesin[5]研究了非对称轧制过程。结果表明,剪切应变在非对称轧制铝合金的晶粒细化中起着关键作用。B.F. Li[6]测试了非对称轧制复合材料的微观结构和性能。结果表明,非对称轧制后铝基体的平均晶粒细化并提高了硬度。
非对称轧制具有改善中心区域板变形的能力,但是由于上、下工作辊的线速度不同,将出现弯曲问题。Mousavi[7]通过有限元方法模拟了非对称薄板的轧制。在其工作中,研究了工作辊速度失配对弯曲曲率、轧制力和轧制扭矩的影响。L. Hao[8]通过有限元模型研究了不同轧制半径引起的非对称轧制后的弯曲曲率,并通过实验研究了轧制半径失配作为弯曲曲率控制方法的有效性。Qwamizadeh[9-10]通过主应力法研究了非对称薄板轧制后的弯曲曲率。
蛇形轧制兼备增强厚钢板中心变形并保持厚钢板形状的优点,引起了许多学者的关注。S.Y. Li[11]和G.F. Xu[12]研究了蛇形轧制后铝合金板的组织和织构,证实蛇形轧制可以细化铝合金板中心的晶粒尺寸并改善机械性能。T.Zhang和J.X. Yang[13-16]通过数值和实验方法分析了蛇形轧制过程中铝合金板的变形行为和温度分布。研究了轧辊偏移,压下量和异速比对弯曲行为和塑性应变在厚度方向分布的影响。由于中性点位置的不同,蛇形轧制变形区组成会有不同[17-18],目前已有的曲率解析模型并不适用。因此,有必要根据变形区的组成,建立蛇形轧制弯曲曲率解析模型。
1 蛇形轧制模型
为了建立蛇形轧制的力学模型,本文提出假设:
(1)厚钢板的宽厚比很大,宽展相对很小可以忽略不计,因此塑性变形可以简化为平面应变问题。
(2)与钢板相比,工作辊的变形可以忽略,因此工作辊可以设置为刚体。所轧制的材料符合Von Mises屈服准则。
(3)上、下工作辊的直径相同,上工作辊的线速度小于下工作辊的线速度。且轧件在通过辊缝时,同步咬入。
图1为蛇形轧制塑性变形示意图,其中坐标系原点位于上工作辊抛出点,x轴方向与轧制方向相反。由于上、下工作辊存在错位量及表面线速度不同,所以上、下工作辊的中心点的位置也不相同。因此,蛇形轧制变形区可分为四个不同的区域,如图2所示。

图1 蛇形轧制示意图
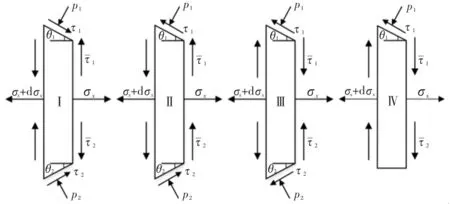
图2 变形区中基元体的受力情况
(1)当上工作辊中性点位于辊缝入口内,下工作辊中性点位于辊缝出口内,此时变形区由I、II、III和IV四者组成。
(2)当上工作辊中性点位于入口内,下工作辊中性点位于辊缝出口以外,此时变形区由I、II和IV三者组成。
(3)当上工作辊中性点位于辊缝入口外,下工作辊中性点位于辊缝出口外,此时变形区由II和IV组成。
1.1 屈服准则
变形区内任意一点服从Von Mises屈服准则,平面应变条件下可得
(1)
(2)
式中,c1和c2为引入系数[19],在搓轧区c1=c2=1,在其他区c1=c2=0.5。

可得
(3)
1.2 塑性变形区单位压力
由于上、下轧辊半径相等R1=R2=R,轧板上下部分的厚度变量可表示为
(4)
于是得到轧板总厚度变量
h=h0+[x2+(x-d)2]/2R
(5)
变形区单元在水平方向的受力平衡方程为
d(σxh)+(p1tanθ1+p2tanθ2-e)dx=0
(6)
I区内的受力具有以下关系
p1=p-1tanθ1,p2=p-2tanθ2,e=1+2,代入(6)并对其中x积分可得I区内的单位压力为
(7)
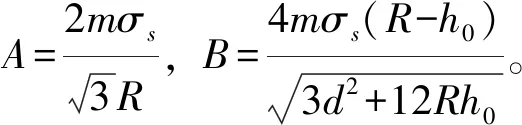
II、III和IV区受力关系分别为
p1=p+1tanθ1,p2=p-2tanθ2,e=2-1;
p1=p+1tanθ1,p2=p+2tanθ2,e=-1-2;
p1=p+1tanθ1,p2=0,e=-1。
同理可得II、III和IV区内的单位压力分别为
1.3 剪切应变引起的弯曲曲率
根据流动准则,轧板上、下部分的剪切应变的微分可表示为
(9)

考虑轧辊间隙中上、下部平均值的情况,可得
(10)


CII(x=xn1)=CII(x=xn2)
(11)
轧制过程中的金属材料体积保持不变,因此
(12)
联立式(11)和式(12)即可求得xn1和xn2。
I区轧板上、下部分的剪切应变方向相反,单元剪切应变可表示为dλI=(dλxy2-dλxy1)/2。同理II、III和IV区单元剪切应变分别为:dλII=(dλxy1+dλxy2)/2,dλIII=(dλxy1-dλxy2)/2,和dλIV=dλxy1/2。因此,轧板在I、II、III和IV区内的角位移可以通过式(13)计算
(13)

(14)
(3)当变形区由II和IV组成。整理可得II和IV区角位移分变为
(15)

1/r1=αT/l
(16)
1.4 轴向应变引起的弯曲曲率
根据流动准则,轧板上、下部分在x方向上的应变微分可表示为
(17)
对式(17)分别在(0,h1)和(-h2,0)范围上积分,因此轧板上、下轴向应变差所引起的弯曲曲率可由下式计算得到
(18)
式中,C为相关系数,与板厚H和偏移量d有关。
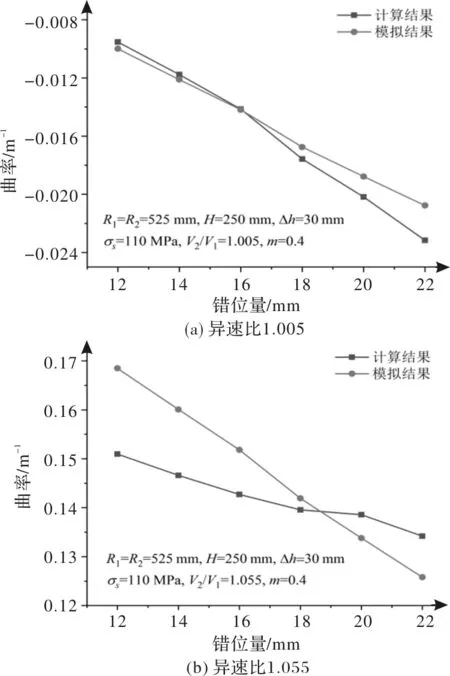
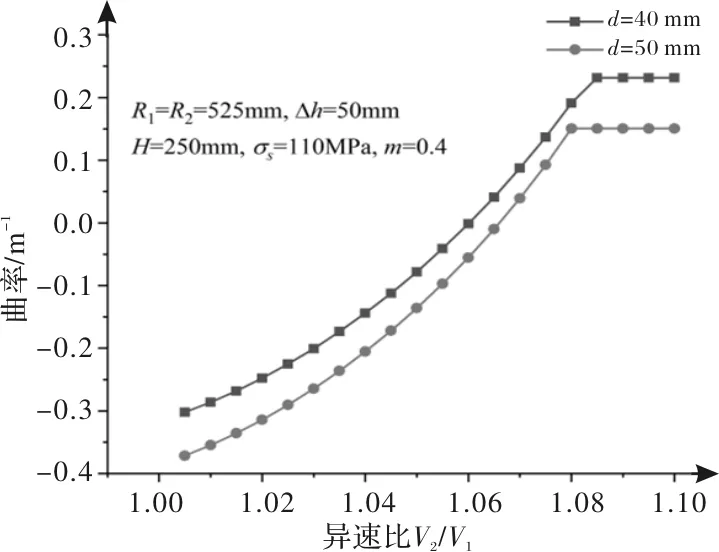
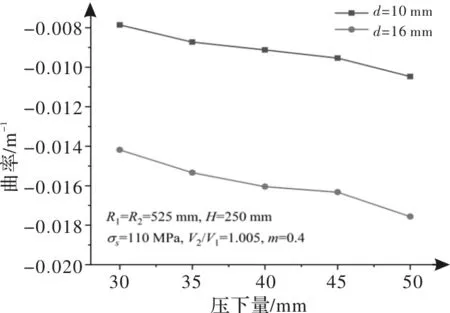
当四个区域存在时,0 轧板总的弯曲曲率为剪切应变引起的弯曲曲率和轴向应变引起的弯曲曲率之和,即 1/r=1/r1+1/r2 (19) ANSYS LS-DYNA为显示动力分析有限元程序,可用于金属塑性成形模拟[20-21],因此使用该软件来模拟同径异速蛇形轧制的过程。由于本模型忽略宽展,模拟采用二维模型。模拟所需数据如表1所示。最后得出不同参数的变化对弯曲曲率的影响情况。 表1 轧制参数 将数值模拟的弯曲曲率与理论计算的曲率结果进行对比,如图3所示。由图3可以看出,当异速比分别为1.005和1.055时,最小相对误差分别为0.3%和1.7%,最大相对误差分别为10.4%和11.6%。与数值模拟相比,所建立模型的相对误差小于12%,此精度在当前条件下可以满足工艺需要。 图3 数值模拟与理论计算结果对比 如图4所示为不同错位量对弯曲曲率的影响,图4a是异速比为1.005时不同错位量下的弯曲曲率。此时,根据计算的xn1和xn2,变形区域由四个区域(区域I,II,III和IV)组成。当异速比较小时,板向下弯曲,计算出的曲率值为负。曲率的绝对值大小随错位量的增加而增加,表明板向下弯曲的幅度越大。 图4b是异速比为1.02时不同错位量下的弯曲曲率。此时,根据计算出的xn1和xn2,变形区域由三个区域(区域I,II和IV)组成。当错位量较小且压下量为30 mm时,板向上弯曲,然后随着错位量的增加而向下弯曲。当压下量为50 mm时,随着错位量的增加,板向下弯曲趋势更加明显。 图4c是异速比为1.055时不同错位量下的弯曲曲率。此时,根据计算出的xn1和xn2,变形区域由两个区域(区域II和IV)组成。此时曲率值为正,表示板向上弯曲。曲率随着错位量的增加而减小,轧板向上弯曲幅度减小。 图4 不同错位量对弯曲曲率的影响 图5所示为当上、下工作辊的线速度分别为1.30~1.43 m/s和1.30 m/s时,本文建立的模型计算出的弯曲曲率。对于给定的错位量,随着异速比的增加,曲率从负变正,并且当异速比达到一定值后,曲率值几乎保持相同。轧板从向下弯曲逐渐变为向上弯曲,并且在异速比达到一定值后保持不变。 图5 不同异速比对弯曲曲率的影响 图6所示为压下量分别为30 mm、35 mm、40 mm、45 mm和50 mm时的弯曲曲率。从图6可以看出,曲率值的绝对值大小随压下量的增加而增加,在图中所示参数的设置下,板向下弯曲。因此,压下量可以使板在相同条件下更弯曲。 图6 不同压下量对弯曲曲率的影响 图7显示了当初始板厚分别为150 mm、200 mm、250 mm、300 mm和350 mm时的板曲率。从图7可以看出,曲率值的绝对值随着初始板厚的增加而减小。在图中所示参数的设置下,板向下弯曲。在相同条件下,若初始板厚越厚,板材更不易弯曲。 图7 初始板厚对弯曲曲率的影响 (1)利用主应力法根据变形区的不同组成,建立了用于计算相同辊径的蛇形轧制弯曲曲率的解析模型。由于应变沿厚度方向的不均匀性,数值结果与理论结果之间存在偏差,但可以控制在0.3%~12%以内,验证了解析模型的准确性。 (2)剪切应变引起的弯曲曲率会使板向上弯曲。而由轴向应变引起的弯曲曲率可使板向下弯曲。随着异速比的增加,变形区域的组成将从四个区域,三个区域变为两个区域。在给定的错位量下,曲率值会随着异速比的增加而从负变为正,并且在达到一定的异速比后不会改变。 (3)错位量、异速比、压下量和初始板厚会对弯曲曲率产生一定的影响。该模型为基于板材的一定曲率要求的工艺参数优化提供了依据,可为工艺参数的设置提供重要参考。1.5 总的弯曲曲率
2 结果讨论与分析




3 结论
