单缝流体推力矢量喷管的气动特性
2020-06-29王建明栾思琦齐晓航毛晓东王成军
王建明, 栾思琦, 齐晓航, 毛晓东, 王成军
(沈阳航空航天大学航空发动机学院,辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136)
推力矢量喷管分为机械推力矢量喷管[1-2]和流体推力矢量喷管。流体推力矢量喷管是指喷管在非机械偏转状态下,通过注入二次流来达到控制主流方向进而实现气流的矢量偏转[3]。根据原理不同,可分为多种控制方式:激波矢量控制[4]、双喉道控制[5]、逆向流法[6]、同向流法[7]等。激波矢量控制技术由于结构简单、矢量效率高已成为航空届的重点研究方向[8-9]。激波诱导矢量喷管的工作机理是在喷管扩张段引入二次流,二次流和主流相互作用生成诱导激波,诱导激波的存在导致了激波后的强逆压梯度的生成,逆压梯度沿亚声速边界层传递至激波前,导致诱导激波前回流区的生成,进而生成了分离激波,两道激波相交称为“λ”激波,主流经过激波后实现了矢量偏转。
李志杰等[10]对激波控制的二元收扩流体推力矢量喷管进行了数值模拟,研究自由流马赫数(Ma),喷管落压比(nozzle pressure ratio, NPR),主次流总压比(secondary pressure ratio, SPR)相同时,不同二次流喷射位置对喷管矢量角及其他喷管性能参数的影响,研究指出二次流喷射位置对推力矢量角有较大影响,但置对推力系数的影响不明显,落压比是影响推力系数变化的主要因素。徐学邈等[11]研究了9组不同射流角下的二元矢量喷管流场,得出射流垂直壁面注入时产生的推力矢量角最大,逆流注入气流对喷管流场的改变要明显大于顺流注入气流的影响, 但产生的损失也较大。吴晓军等[12]采用数值模拟手段对流体二次引射推力转向参数影响规律进行了研究,得出不同参数对干扰流场结构和推力转向偏角的影响,最终得出流体二次引射实现推力转向的基本设计原则及较优的参数组合方案。王猛杰等[13]通过研究喷管落压比影响矢量角机理及基于多缝腔体和多缝辅助注气方法的分离区控制,得知矢量性能随落压比增大而下降主要是由次流下游分离区的结构变化导致的,并最终得到环境压力的多缝辅助注气可以在不增加系统额外引气量的条件下使得大落压比时的矢量性能得到提高。宋亚飞等[14]对基于激波控制的二维射流推力矢量喷管非定常流场进行研究,分析二次流总压连续变化对喷管流场和推力性能的影响,结果表明喷管扩张段注入二次流的总压增加到一定程度才可以实现推力矢量控制。史经纬等[15]考虑到变比热合及温度对传热系数、黏性系数的影响,对次喷喷口几何构型在不同喷管NPR、SPR工况下的二维流动特性及推力矢量特性进行了研究,指出在大的二次流压比下,诱导激波会与喷射壁面相交,导致推力矢量效率的恶化。Song等[16]提出了一种新型的混合SVC喷管,在传统SVC喷管的基础上将超声速气流通过喷管的上下壁面横射入超声速主流,并对喷管的基本流动机理、气动参数和几何参数对其性能的影响进行了计算研究。Neely等[17]采用小尺度超声速喷管研究射流推力矢量控制技术,测量了一定NPR(10~30)、SPR(0.012~0.11)范围内喷管的纹影可视化和双组分推力。在二次流的喷射压力足以在二次流喷口对侧壁的唇口处造成诱导激波的情况下,获得约5°的最大矢量角。He等[18]对圆-矩形喷管进行三维数值模拟,研究了不同SPR下二次喷射角和槽长对喷管流动特性和推力性能的影响。Forghany等[19]研究了不同自由流马赫数(Ma=0.05~1.1)对收扩喷管推力矢量控制的影响。研究指出增加自由流马赫数会降低推力矢量控制效果,优化射流角度可以减少外部自由流对推力矢量控制性能的负面影响,在不同自由流工况下增大SPR和减小NPR,都可以缩短启动射流推力矢量过程的响应时间。
目前的推力矢量喷管研究大多针对喷管的定常性能参数,而关于研究喷管的非定常流动结构的报道较少。为此,采用数值模拟方法求解2DCD矢量喷管的非定常流场,并通过对喷管对称面上的流线、涡量系数、密度梯度和熵的分布等的具体分析,得出喷管流场的非定常流动特性。
1 计算模型和数值方法
1.1 计算模型和网格
激波诱导矢量喷管模型选自文献[20]。喷管主要设计参数如表1所示。

表1 喷管主要设计参数Table 1 Main designed parameters of the nozzle
喷管计算域和全局网格如图1(a)所示。二次流喷口和喷管壁面处进行了加密处理,如图1(b)所示。全场采用六面体结构化网格,总数约250×104。近壁面第一层网格高度为0.01 mm,y+<1。
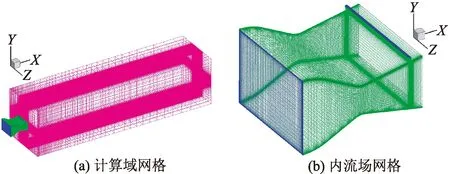
图1 计算域和网格Fig.1 Computational domain and grids
1.2 计算模型和网格
数值模拟利用FLUENT软件,采用分离涡(detached eddy simulation, DES)[21]进行湍流模拟。DES湍流模型是RANS(reynolds averaged Navier-Stokes)和LES(large eddy simulation)的混合方法,是模拟复杂工程问题中分离流动的一种主要方法[22]。选用基于SST(shear-stress transport)k-ω的DDES(delayed detached eddy simulation)湍流模型。其中,湍动能k的输运方程:
(1)
特定湍流耗散率ω的输运方程:
(2)
式中:ρ为流体密度;u为流体速度;Γk和Γω分别为k和ω的有效耗散系数;Gk和Gω分别为k和ω的产生项;Yk和Yω分别为k和ω由于湍流引起的耗散项;Xω为交叉扩散项。湍动能的耗散项Yk可表示为
Yk=ρβ*kωFDES
(3)
引入DDES概念,通过因子FDES对湍动能消耗项加以修改,FDES表示如式(4)所示:
(4)
式(4)中:CDES为模型常数;Δ为单元网格的最大尺度;Lt为湍流长度尺度;FSST为混合函数。
速度和压力的耦合采用Coupled算法,物理时间步长 Δt=5×10-5s,共计算150个流动周期。计算所用流体为理想气体,流体黏性采用Sutherland公式。所有壁面皆为绝热、无滑移壁面。喷管入口总压为466 095 Pa,二次流入口总压为326 266.5 Pa。
2 计算结果和分析
2.1 计算结果验证
网格数量直接影响着数值模拟的计算精度和收敛速度。为了在保证计算精度的基础上尽可能地加快计算速度,对网格进行独立性验证。如图2所示,分别计算了150×104、200×104、250×104和300×104的网格,横轴为喷管的扩张段坐标,纵轴为扩张段上壁面的压力分布。从图2中可知,当网格数达到250×104时,壁面压力基本不再变化,就此可认定网格数量≥250×104后,计算结果不再发生变化。以此同时计算速度也较为合理。因此选择250×104网格进行计算。
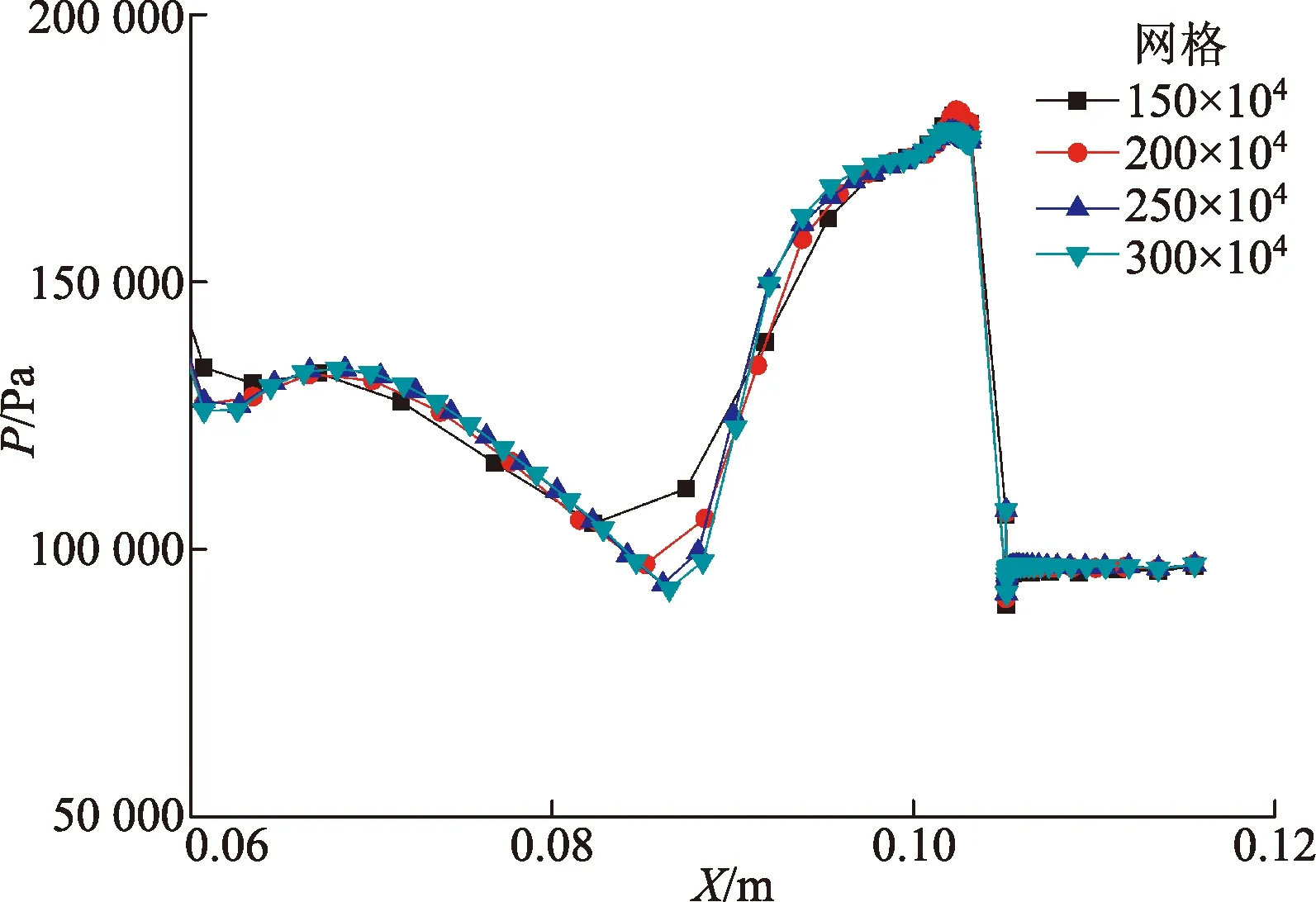
图2 网格独立性验证Fig.2 Verification of grids independence
图3为计算所得喷管的上、下壁面中心线无量纲压力分布与文献[20]实验结果的对比。其中,Xt为喷管喉道的轴向坐标,Pt,m为喷管主流的入口总压。图3说明计算曲线和实验所得曲线的结果基本一致,这进一步证明计算结果具有一定准确性和可信性。
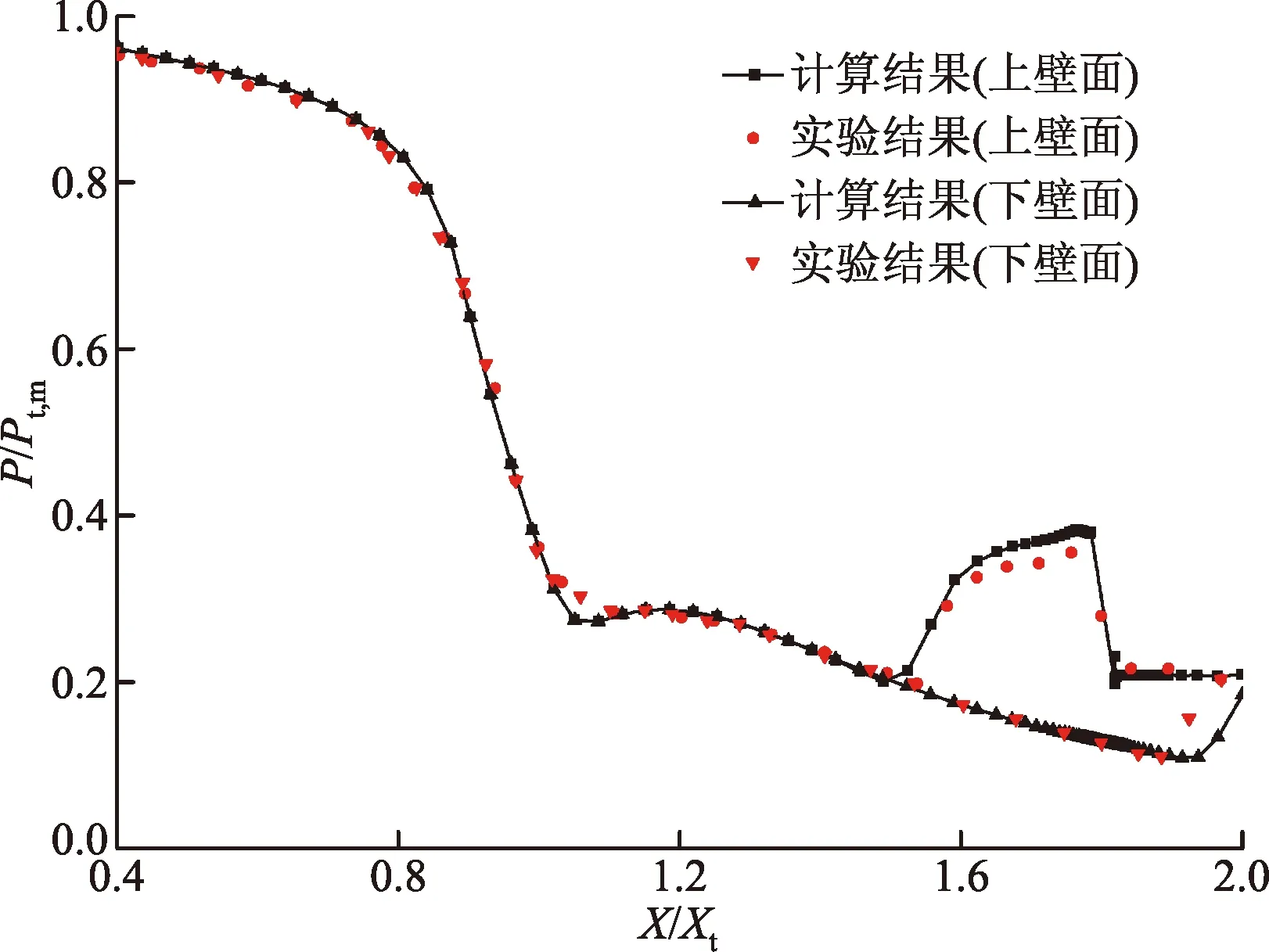
图3 数值计算所得壁面无量纲压力与实验[20]对比Fig.3 Comparison of dimensionless wall pressure between numerical and experimental[20]results
2.2 喷管的流场结构
图4为喷管流场X方向和Z方向系列截面的压力系数分布。压力系数定义为
(5)
式(5)中:Pin为喷管入口压力;ρin为主流入口流体密度,vin为主流入口的流速。
从图4(a)可看到:喷管喉道和收敛段处压力系数显示为红色,为高压分布。超声速主流进入扩张段发生膨胀加速,压力逐渐减小。由于二次流的作用主流被压缩,压力增大。图4(a)可观测到分离激波的位置。图4(b)中,距离二次流较远的上游流场并未受到激波的影响,流场压力系数分布保持上下对称性;受到激波影响区域以X=0.108 m的截面为例,此截面贯穿了二次流喷口前的分离区,截面的压力系数从上到下越来越小,可分为三个区域,这三个区域的生成原因分别为:由二次流引起的流动分离生成的高压区、流经分离激波后增压减速的流动以及未流经分离激波的主流。未流经分离激波的主流相较其他区域仍然保持低压高速状态。沿流向,未流经分离激波的主流区域越来越小。从图4可知喷管的对称面处结构是接近对称的,因此可以用对称面的流动结构揭示三维流场,从而更直观地分析流场的结构变化。
运用Q准则[23-24]来清晰识别喷管内流场的旋涡结构。Q准则是速递梯度张量的二次不变量[25],速度梯度可表示流体运动中的角变形率,Q可定义为
(6)
式(6)中:Ωij为速度梯度的反对称张量;Sij为速度梯度的对称张量,分别定义为
(7)
(8)
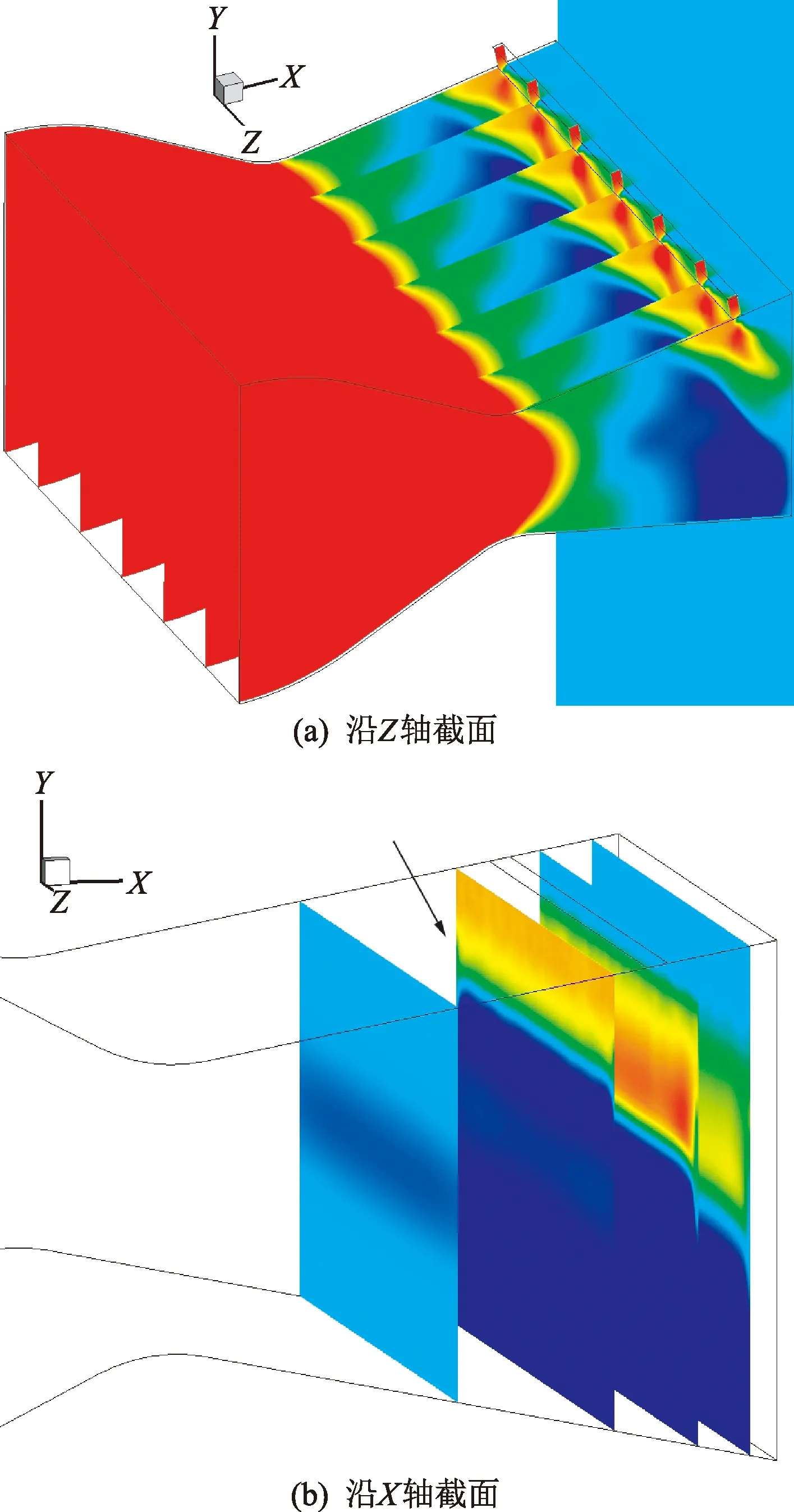
图4 喷管内流场压力系数分布Fig.4 CP distribution of flow field in the nozzle
图5是喷管流场的Q准则等值面图。在图5中可观测到二次流喷口前后分离区中涡系的存在。图6为二次流入口附近流线分布。需要说明的是,三维流线一般不会处于同一个二维平面上,但如前所述由于流场结构的对称性,因此用喷管对称面上的X-Y速度矢量线来近似代替流线。对比图5、图6可知,二次流喷口前涡的生成机理是诱导激波的存在生成的分离涡,以及由于流动引射生成的诱导涡,二次流喷口后的主流在高压二次流的作用下不再附着于上壁面,因此外流场气流绕过喷管上壁面唇口进入内流场,进而生成了绕流涡,以及在绕流涡和主流间生成的诱导涡。
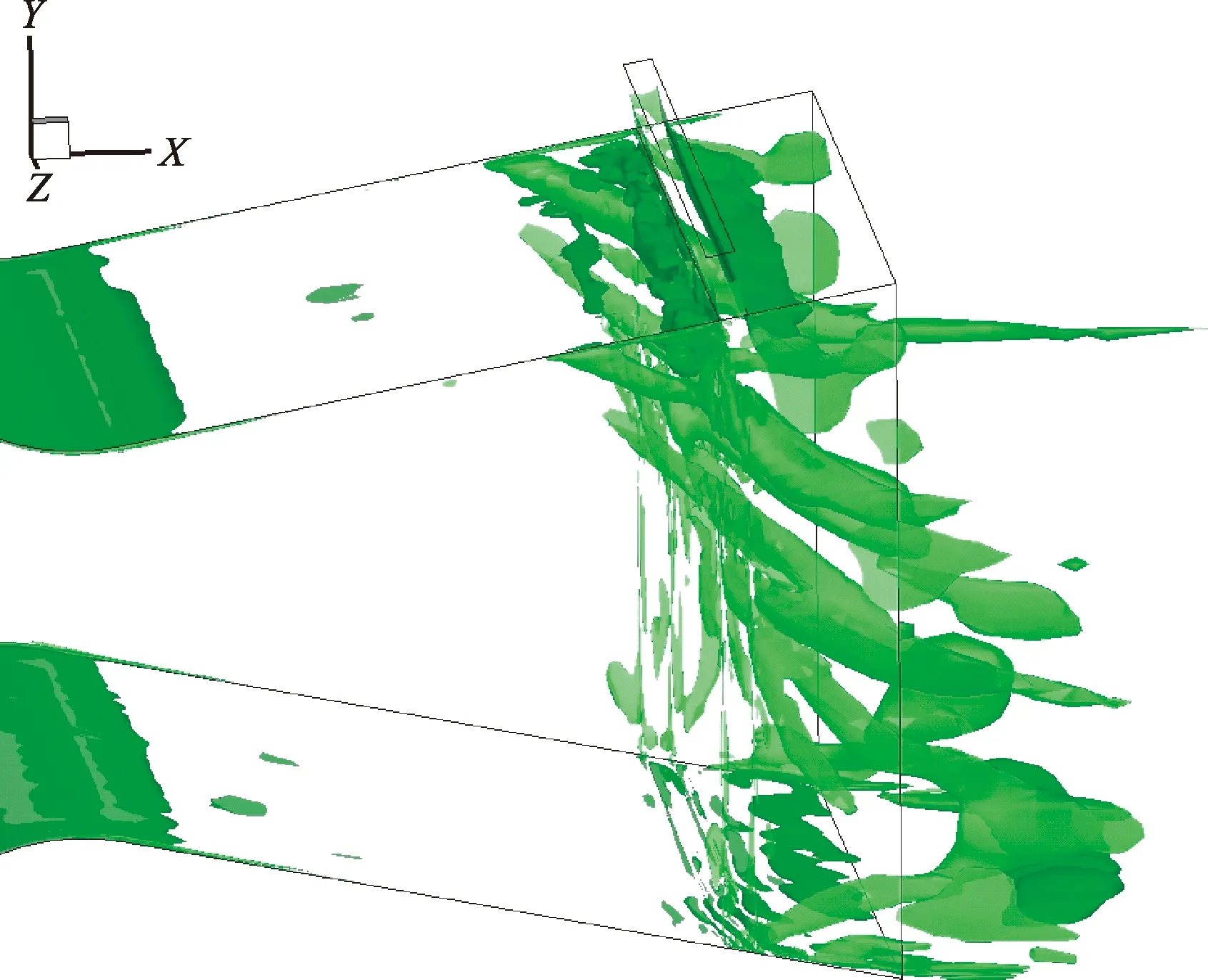
图5 喷管内流场旋涡结构Fig.5 Vortex structure of flow field in the nozzle
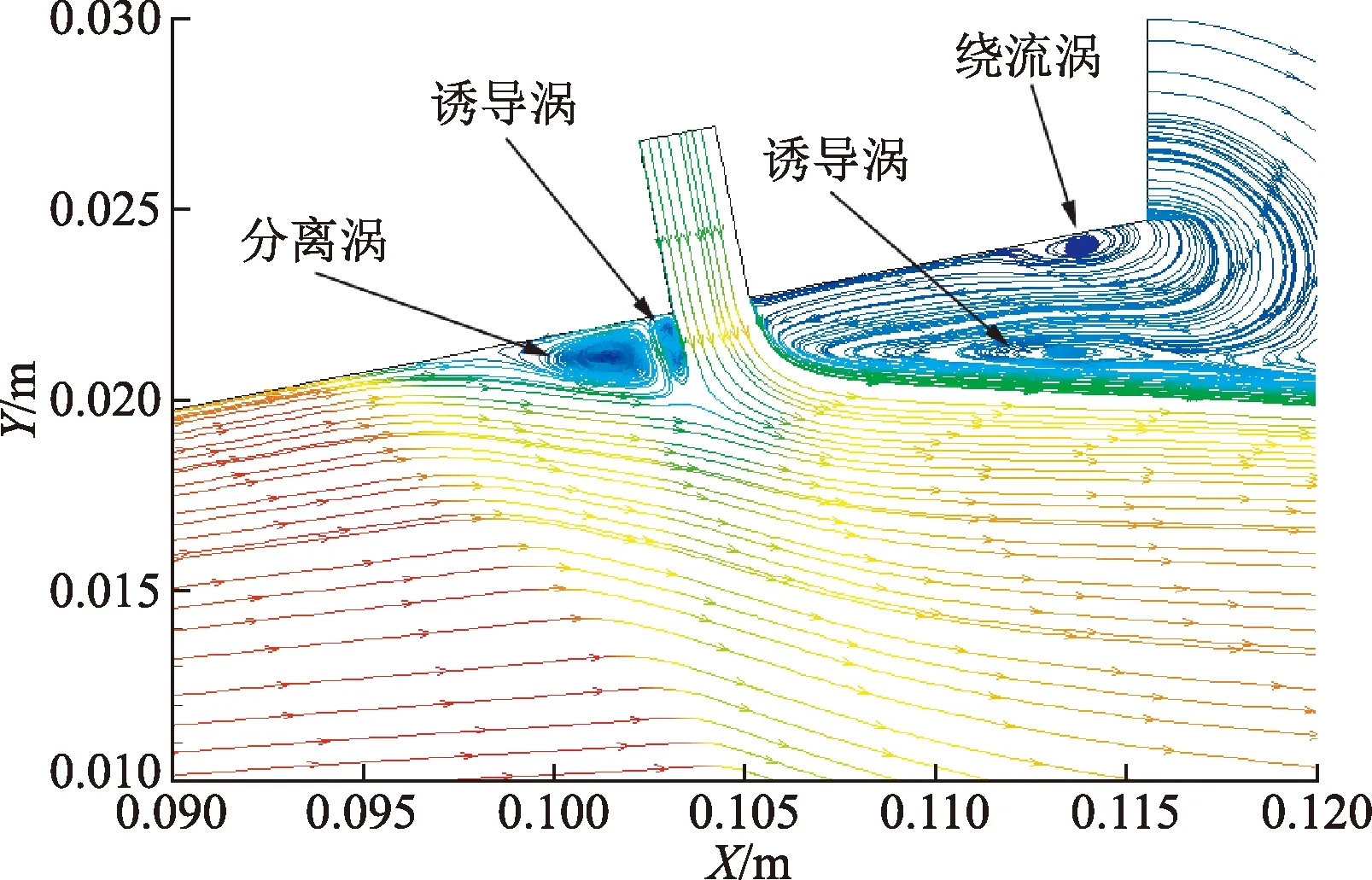
图6 二次流入口附近流线分布Fig.6 Streamlines distribution near the secondary flow inlet
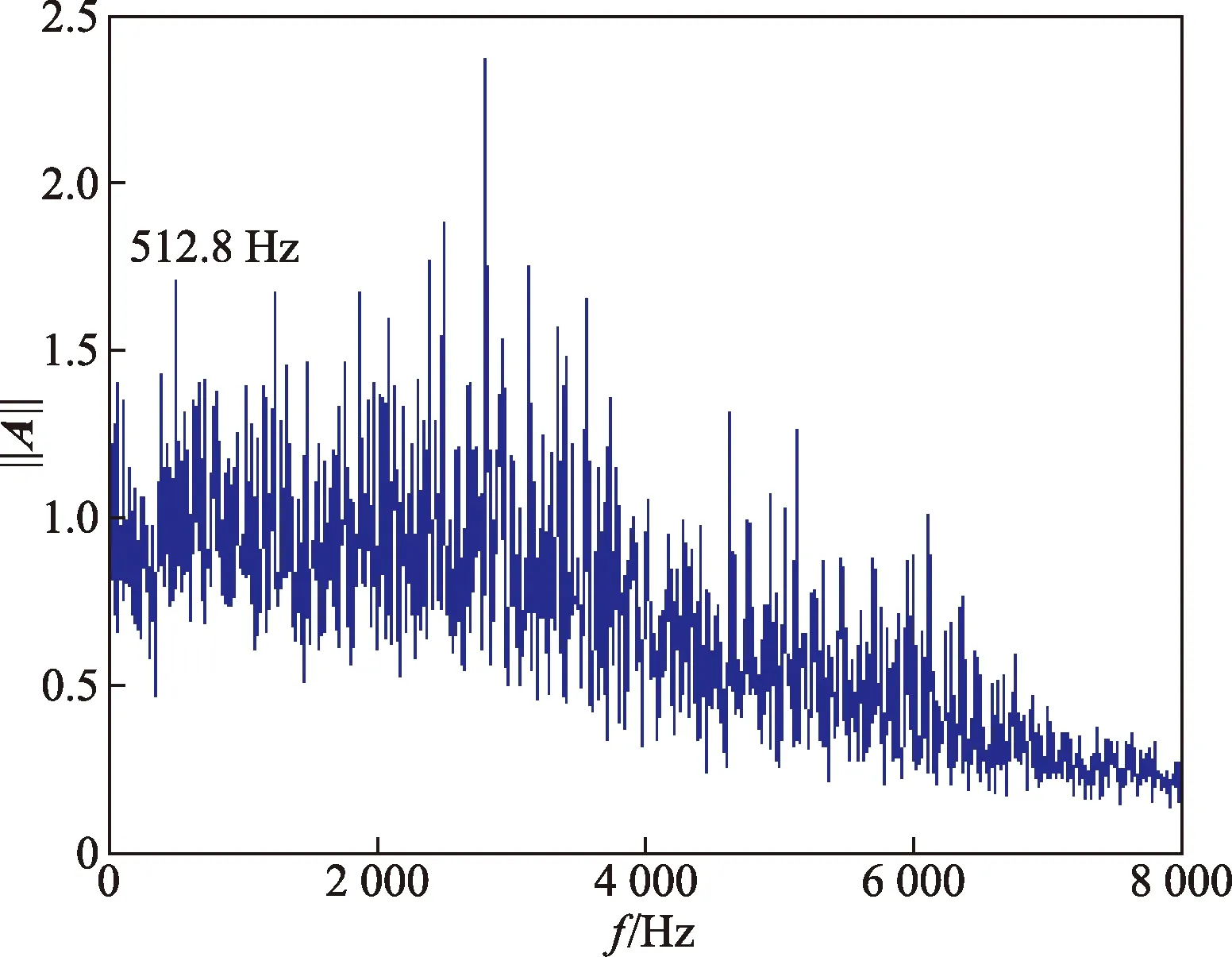
图7 FMD幅频曲线Fig.7 FMD amplitude-frequency curve
接下来分别从一个周期中喷管的流线、涡量系数、密度梯度和熵的变化分析喷管的流动结构。周期取决于对喷管流场做傅里叶模态分析(Fourier mode decomposition, FMD)得出的一阶频率,为512.8 Hz(图7);FMD的具体内容见文献[26]。流线、涡量系数、密度梯度和熵增所选用的图片是由相同时刻的数据后处理得到的。
图8为一个周期内喷管对称面上的流线分布。流线不同颜色代表了X、Y方向合成速度的大小。由于尾流和外部气流的速度差和流体黏性的影响,尾流上、下侧会生成剪切层。T/6时刻,从上壁面唇口处脱落的上层涡1运动至X=0.12 m处,从下壁面唇口处脱落的下层涡1位于X=0.155 m处;2T/6 时刻,上层涡1继续向下游脱落,已运动至X=0.125 m处,下层涡1运动至X=0.17 m处;(3/6- 4/6)T时刻,上层涡1从X=0.14 m运动至X=0.155 m处,下层涡1从X=0.175 m运动至X=0.19 m处,同时可观测到下壁面唇口处新生成的下层涡2已脱落至X=0.13 m处;5T/6时刻,上层涡1运动至X=0.16 m处,下层涡1运动至X=0.195 m处,下层涡2运动至X=0.135 m处;T时刻,上壁面唇口处新生成的上层涡2即将脱落至T/6 时刻上层涡1的位置,下层涡2即将脱落至T/6 时刻下层涡1的位置。T/6时刻和T时刻流场结构类似。通过流线分布可知上、下壁面的唇口处不断有涡沿着剪切层外侧向下游脱落,脱落的过程中伴随着旋涡空间尺度的变化。
涡量系数定义为
(9)
式(9)中:Vvor为涡量;L为喷管特征长度。
图9为一个周期内喷管对称面涡量系数的变化。二次流喷口前侧涡量的波动是由于分离区的分离涡和诱导涡的振荡所致。尾流的上剪切层处涡量系数显示为红色, 说明上剪切层内的旋涡为逆时针旋转的涡,下剪切层处涡量系数为负,下剪切层内的旋涡为顺时针旋转的涡。由于上壁面唇口处绕流涡和诱导涡的振荡等因素,上剪切层的摆动角度明显强于下剪切层。上剪切层的摆动是尾流振荡的主要原因之一。
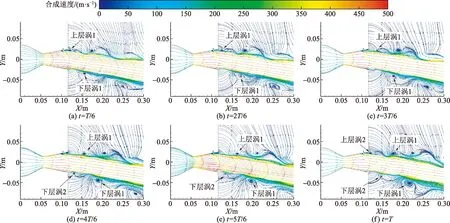
图8 喷管对称面流线分布Fig.8 Streamlines distribution at Z=0
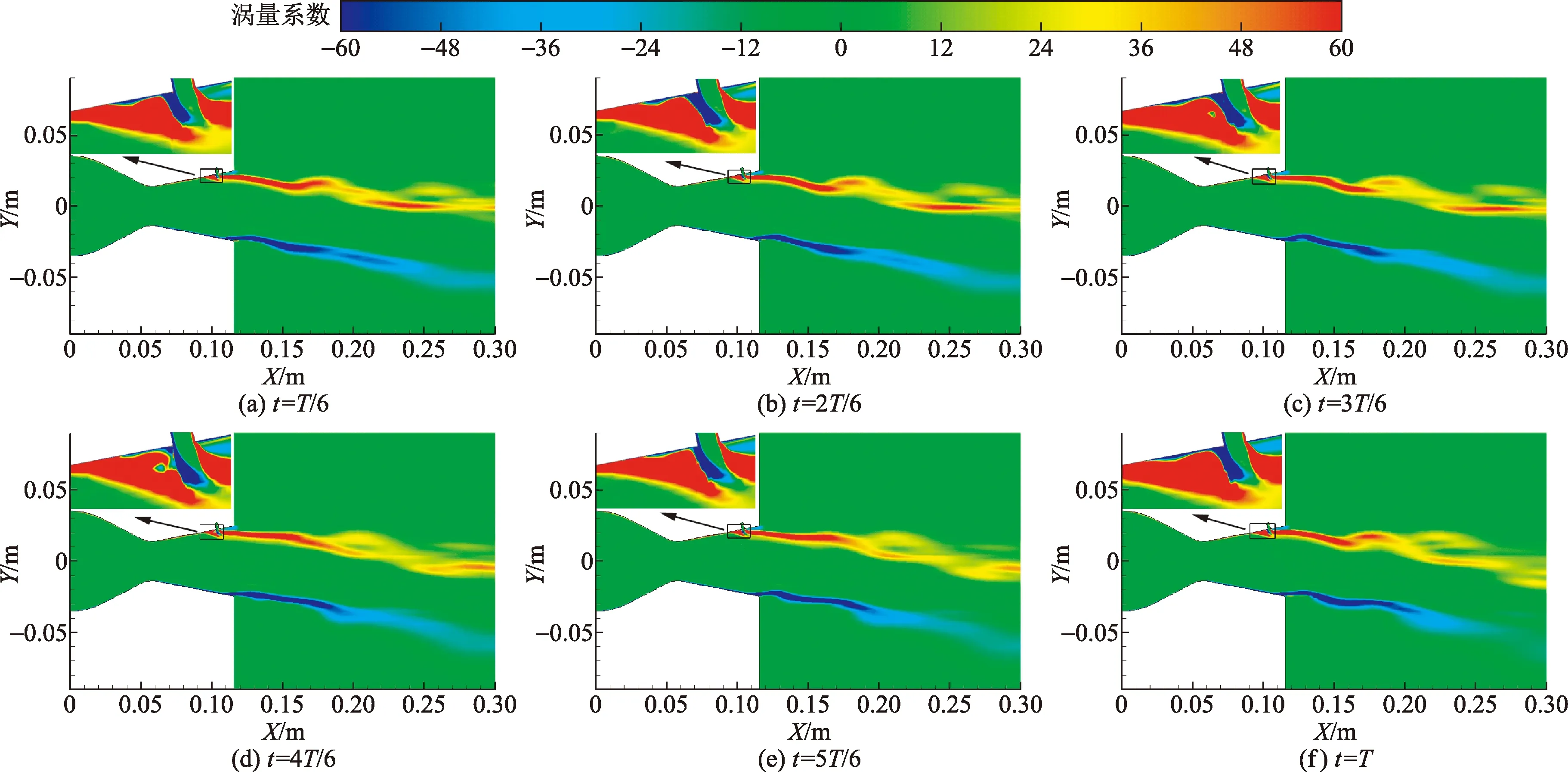
图9 喷管对称面涡量系数分布Fig.9 Vorticity coefficient distribution at Z=0
图10、图11分别为喷管对称面一个周期的X方向和Y方向密度梯度分布。由于下壁面唇口处回流区的存在,使得此处剪切层向内凹陷,主流在λ波前被压缩,生成了一道反射激波,反射激波与λ波在靠近下壁面处相交。λ波与尾流的自由边界相交,反射出膨胀波系。在图10、图11中皆可观测到λ波、反射激波和膨胀波的具体位置。激波随着流动的发展是不断发生振荡的λ波的振荡是由于二次流喷口前的分离区中涡的不断振荡,改变了分离区尺度引起的,反射激波的振荡是因为下壁面唇口处涡系的振荡和脱落引起的。图10的喉道处的密度梯度为负,清晰地观测到主流在经过喉道处时发生的膨胀。λ波作为强激波在图10的X方向的密度梯度分布和图11的Y方向的密度梯度分布皆为红色,显示为密度增大,流体在此处被压缩。反射激波在图10的X方向密度梯度分布为红色,显示为压缩状态;在图11的Y方向密度梯度分布为蓝色,在Y方向发生膨胀;反射激波作为一道压缩波,X方向密度梯度占主导位置。膨胀波与反射激波恰好相反,在图10的X方向密度梯度分布为蓝色,在图11的Y方向密度梯度分布为红色,X方向密度梯度占主导位置。图11的Y方向的密度梯度可观测到尾流处剪切层的密度梯度,上剪切层为负,下剪切层为正,说明上剪切层处于膨胀状态,下剪切层被压缩;图10的X方向尾流剪切层的密度梯度趋近于0。
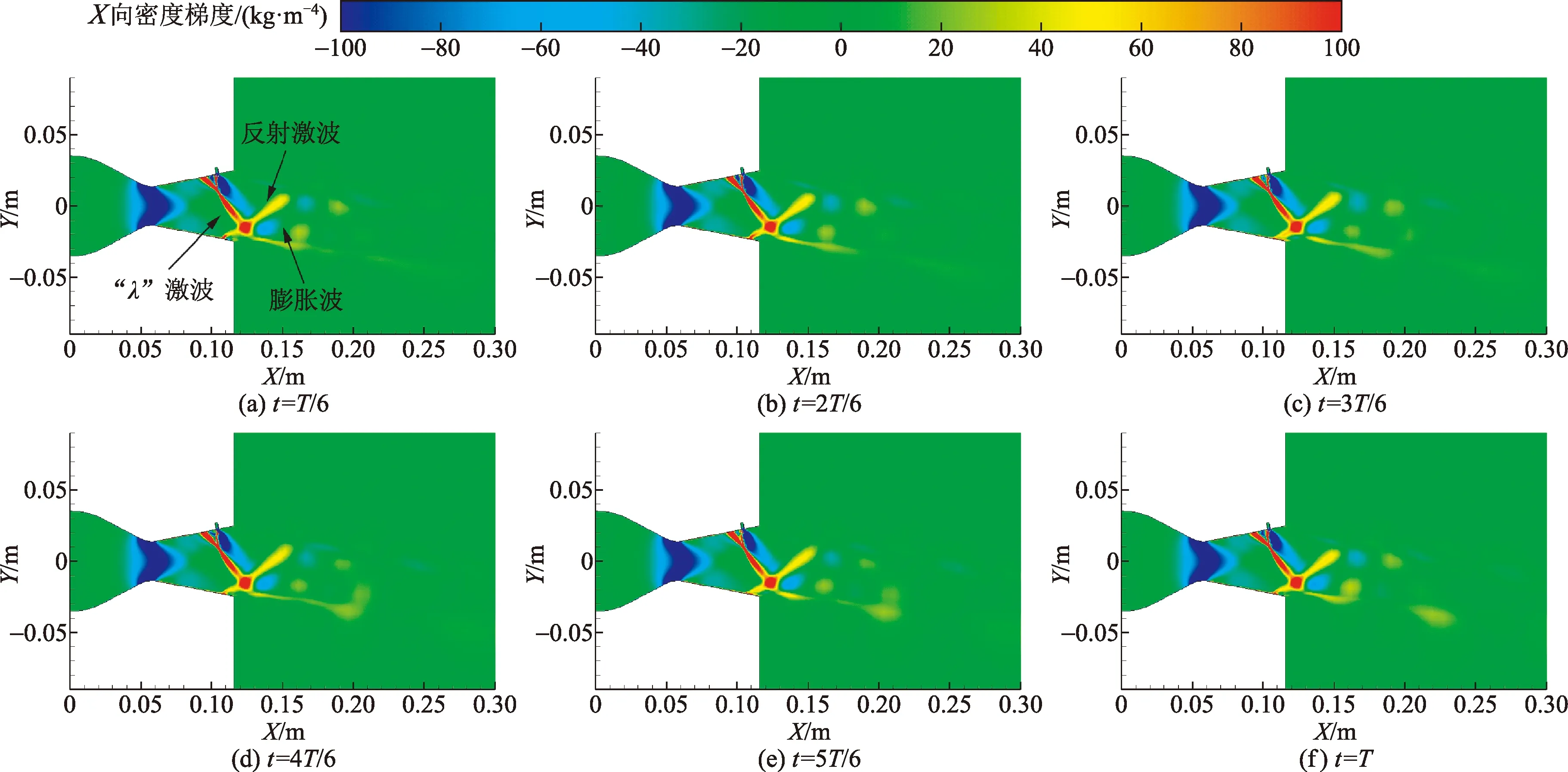
图10 喷管对称面X方向密度梯度分布Fig.10 The X-direction density gradient distribution
图11 喷管对称面Y方向密度梯度分布Fig.11 The Y-direction density gradient distribution
图12为喷管对称面一个周期相对于主流入口的熵增分布,可观测到λ波和反射波的存在。λ波的上游流场熵分布均匀,主流经过λ波后实现了熵增,同时熵分布不再均匀,忽略剪切层部分,主流熵增为50~110 J/(mol·K)。经过反射激波后主流并无明显熵变化。喷管内流场中分离区的熵增最大,因为分离区存在涡的振荡导致流场混乱度增高。随着流动时间的发展,尾流在发生能量耗散的同时伴随着熵增,如图12中圈示部分。外流场中,喷管尾流熵的最大值位于剪切层处,剪切层由内到外熵越来越大,熵值跨度约为210 J/(mol·K)。剪切层熵增是由于剪切层的摆动增大了其湍流强度,流场的混乱增强;同时,剪切层中的涡不断进行着脱落和振荡,也是熵增的原因之一。
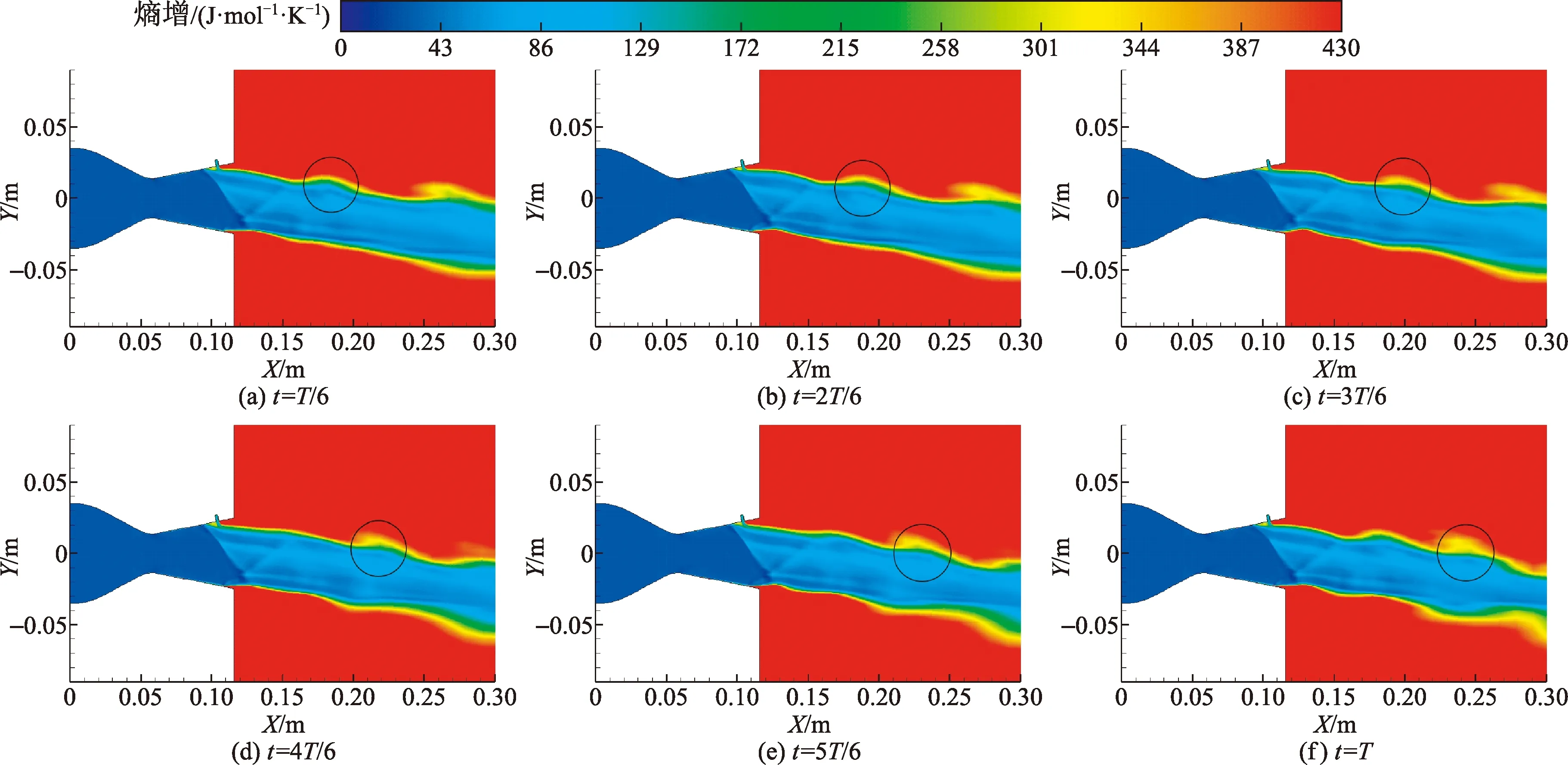
图12 喷管对称面熵增分布Fig.12 Entropy increase distribution
3 结论
运用数值模拟方法研究流体推力矢量喷管的非定常气动特性。通过对矢量喷管的流线、涡量系数、密度梯度和熵的分布的分析,得到如下结论。
(1)随着流动的发展,上下壁面唇口处生成的涡沿着剪切层外侧不断向下游脱落。
(2)二次流喷口前分离区涡系的振荡改变了分离区的尺度,导致了λ波随着流动的发展不断发生振荡;下壁面分离区涡系的振荡和脱落导致了反射激波的振荡。
(3)λ波是强激波。尾流上剪切层为膨胀状态,下剪切层处于压缩状态;上剪切层的摆动角度和熵增皆大于下剪切层。
