体积压裂水平井蒸汽吞吐过程的砂粒运移

刘承婷， 尹井奇

(东北石油大学石油工程学院，大庆 163318；东北石油大学提高油气采收率教育部重点实验室，大庆 163318)

以水平井体积压裂蒸汽吞吐过程为主的稠油油藏开发开采过程，必须解决水平井出砂问题。出砂会引起多方面的问题，一部分细小砂砾会随着产出液来到地面，在产出液输送管过程中造成管线和设备的磨损，严重时可以导致设备的损坏失效。粗砂则会随产出液进入井筒，在井筒内堆积形成砂床会引起井筒砂堵或埋砂油层，继而导致减产或停产产。在蒸汽吞吐进行多个轮次后因受到边水、断层等因素的影响出砂严重，效果变差[1-5]。因此有必要对体积压裂水平井蒸汽吞吐过程中的砂砾运移情况进行研究，对砂床在井筒内的形成条件以及影响因素进行研究，为应对油井出砂问题提供理论依据。

李明忠等[6]借助砂砾在水和煤油中的静态试验，优选出实际油井出砂自由沉降末速的预测公式，并计算得到了砂砾的不规则形状校正系数，通过流动携砂实验获得了砂砾在流动液体种的沉降规律。王冶中等[7]利用研制的井筒携砂实验装置,模拟了一定砂粒配比下不同井型中的携砂情况。观察了颗粒在不同倾斜角度的井筒中的运移方式,测定了不同粒径的砂粒被携带出的临界流量,揭示了颗粒直径同流体流量关系变化规律。雷登生等[8]建立了适合于水平井筒特点的机理模型，为稠油携带物理模拟实验和携带能力计算提供了理论依据。王洪等[9]建立了出砂特征参数分析模型，在常规水平井筒压降求解公式基础上,进一步推导建立了携砂开采情况下水平井筒变质量流压降计算模型,联立了水平井向井流动态关系耦合求解模型。秦宏波等[10]对应用于固液两相流数值模拟中的三种主要模型:单流体模型、两流体模型和欧拉-拉氏模型进行了对比，分析了其各自的优缺点及适用范围，并对商用CFD(computational fluid dynamics)软件PHOENICS中有关固液两相流的处理方法进行了论述，探讨了其在管道输送固液两相流数值模拟中应用的可行性。姚晓刚[11]探讨了稠油油藏热采的概念，分析了水平井的特点，最后探讨新型滤液控砂管技术、分段射孔的完井技术、中心管变密度打孔均衡采油技术这三种技术的应用。

水平井体积压裂蒸汽吞吐过程中，影响砂砾在水平带有裂缝的井筒中运移以及砂床形成的因素有很多，如携砂液的性质、井筒结构及井斜角等[12-15]。基于此对不同条件下的这些因素对砂砾运移情况的不同进行了研究。

1 数学模型的建立

1.1 双流体模型

1.1.1 连续性方程

(1)

1.1.2 湍流方程

以固液混合相为研究对象，综合考虑了液相和颗粒相的湍动作用对流动过程的影响，其k方程和ε方程分别如式(2)、式(3)所示:

ρε+Gb-YM+Sk

(2)

(3)

式中：Gb为湍动能；k为湍流动能；ε为湍动能耗散率；YM为在可压缩流动中，由于扩散而产生的波动；σk、σε分别为k方程和ε方程的湍流Prandtl数,σk=1.0，σε=1.3；Sk、Sε为k方程和ε方程的用户定义的流场湍流参数；s为流场阻力系数；C1ε、C2ε为常数，C1ε=1.44,C2ε=1.92,Cμ=0.09。

2 水平井几何物理模型

2.1 物理模型建立与网格划分

在SolidWorks中建立体积压裂水平井模型(图1)，将模型简化为带有六条圆柱状对称裂缝的水平井，模型尺寸如下：水平井筒长度L=2 000 mm，水平井筒半径R=177.5 mm，裂缝半长l=200 mm，裂缝宽度a=4 mm。在ICEM CFD(integrated computer engineering and manufacturing code for computational fluid dynamics)中进行网格划分，网格的划分对于计算的精度也十分重要，体积压裂水平井模型采用六面体结构网格的划分方式，如图1所示。

图1 六面体结构网格划分示意图Fig.1 Diagram of grid division of hexahedron structure

具有不同裂缝数量的水平井砂床的沉积和砂砾的运移情况是不同的，相同情况下体积压裂水平井的裂缝条数的不同直接影响到混合物的流动速度。考虑到水平井分段多簇体积压裂对井筒内固液两相流流动的影响，不改变井筒长度和直径增加裂缝条数，建立分段多簇压裂水平井模型(模型2)，网格划分方式同上，如图2所示。

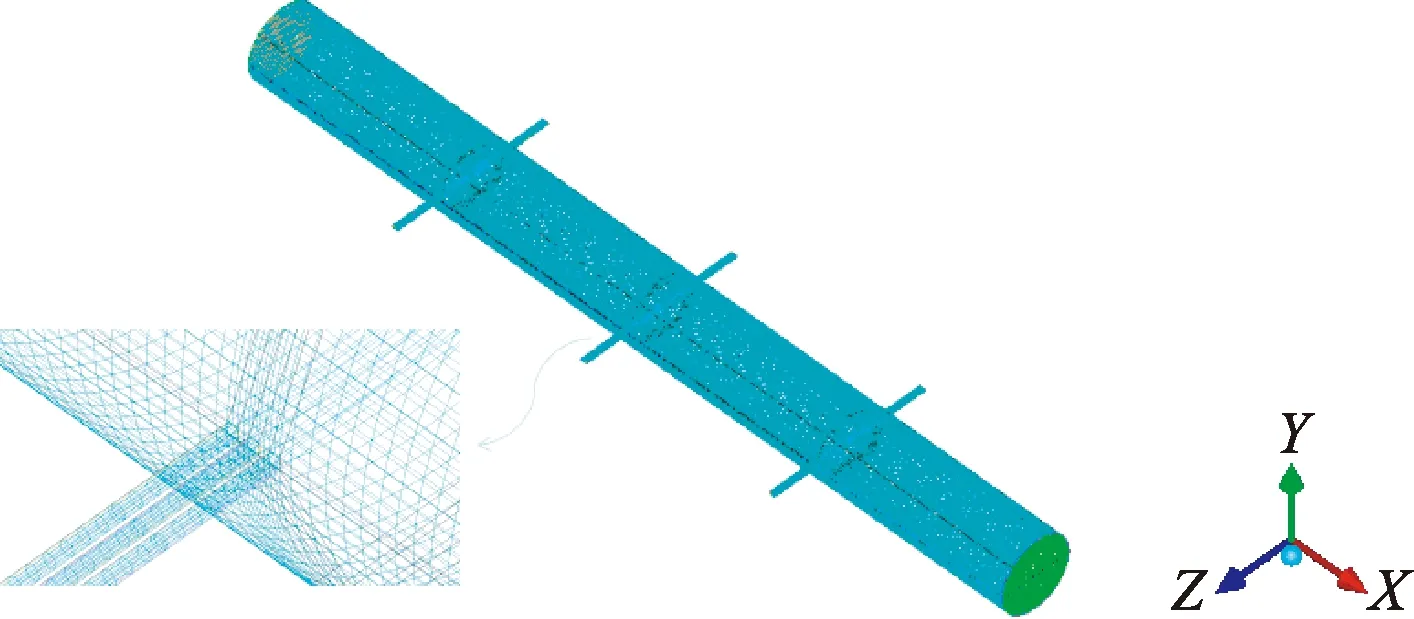
图2 多簇压裂水平井模型Fig.2 Model of multi-cluster fractured horizontal wells

具有不同井斜角的水平井筒内的砂床形成形态和砂砾运移情况存在较大差异。考虑到水平井的井斜角对井筒内固液两相流流动的影响，保留井筒长度井筒直径以及裂缝条数和直径，改变井斜角分别为90°、85°、80°。分别建立模型a、b、c，网格划分同上，如图3所示。

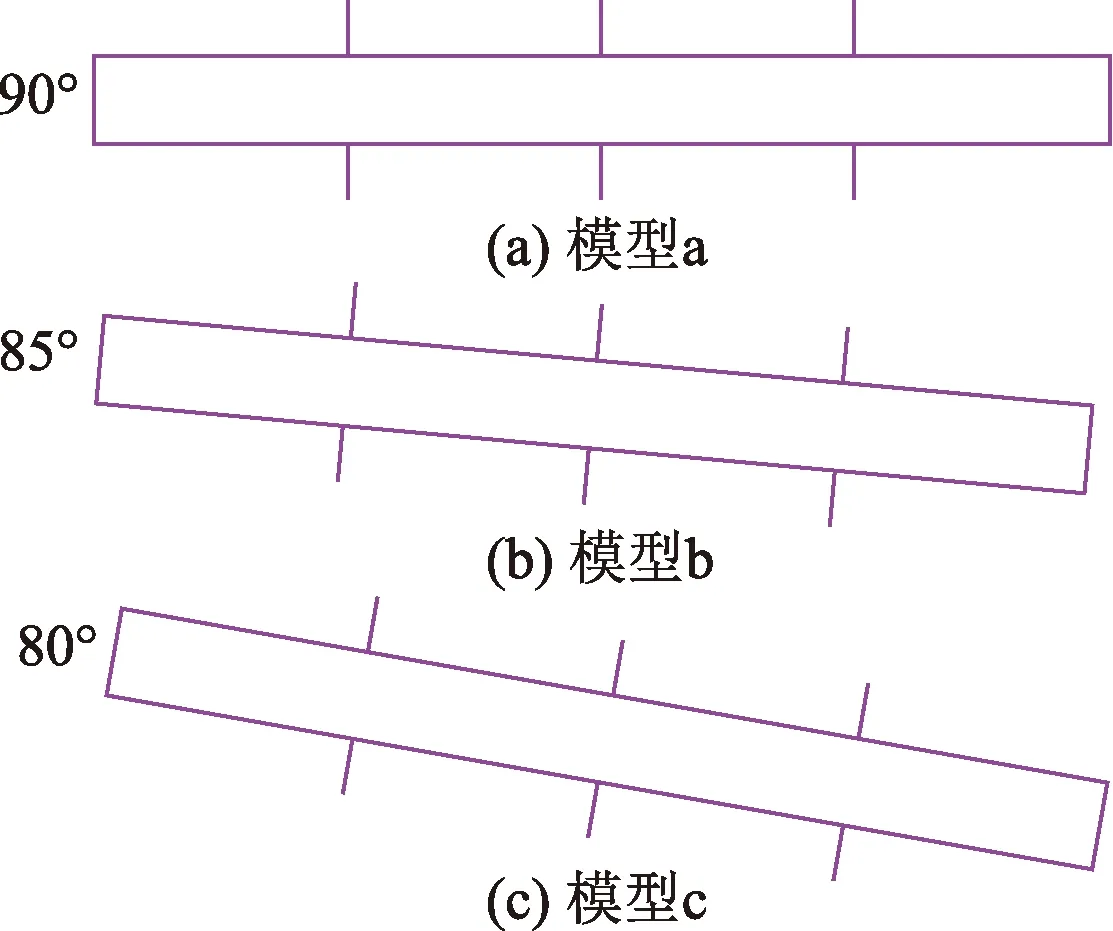
图3 不同井斜角模型示意图Fig.3 Schematic diagram of different well angle models

2.2 边界条件的设定

将网格导入FLUENT，定义入口边界条件为压力入口(pressure-inlet)，出口边界条件为压力出口(pressure-outlet)，定义壁面边界条件为无滑移壁面(wall)。并且设置固液两相流初始条件，包括液相黏度、液相密度、固相密度、固相粒径、固相体积分数。

3 模拟结果及分析

3.1 油藏地层压力

采用图1模拟体积压裂水平井随着生产开发，地层中油藏压力逐渐降低时油井出砂情况，具体的参数设置如下：液相为原油，密度950 kg/m3，黏度0.2 Pa·s；固相为石英砂，粒径为4 mm，密度为2 985 kg/m3，固相浓度为8%。保持井口压力为3 MPa、井筒出口压力为2 MPa，压差为1 MPa恒定；分别模拟裂缝压力由12、10、8、6、4 MPa不同工况条件下，体积压裂水平井井筒内固液两相速度、浓度、等分布情况。整体流畅速度分布云图(图4)。

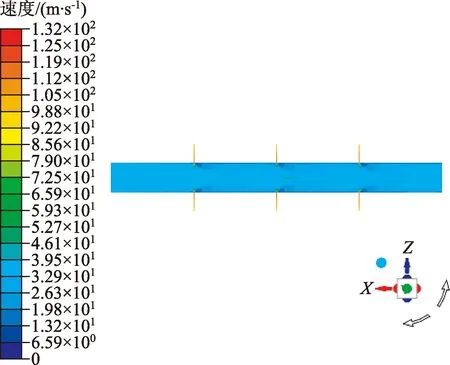
图4 整体流场速度分布云图Fig.4 Velocity distribution cloud chart of the overall flow field

由固相体积分布云图(图5)可以看出，固相浓度在井筒内随着裂缝压力的提高呈现出下降的趋势，当裂缝压力达到8 MPa时固相体积分数达到最小，当裂缝压力再次提高达到10、12、14 MPa时固相体积分数趋于稳定，并没有随着裂缝压力的提高而明显降低。由图5可知，降低出砂率的最佳裂缝压力在8 MPa左右。开发中后期由于地层压力不足造成油井出砂，此时需要补充地层能量提高油藏压力，达到减少出砂的目的，但是油藏压力过高会导致能量的浪费，于是通过模拟不同裂缝压力条件的固相体积分布，来研究最佳的裂缝压力。

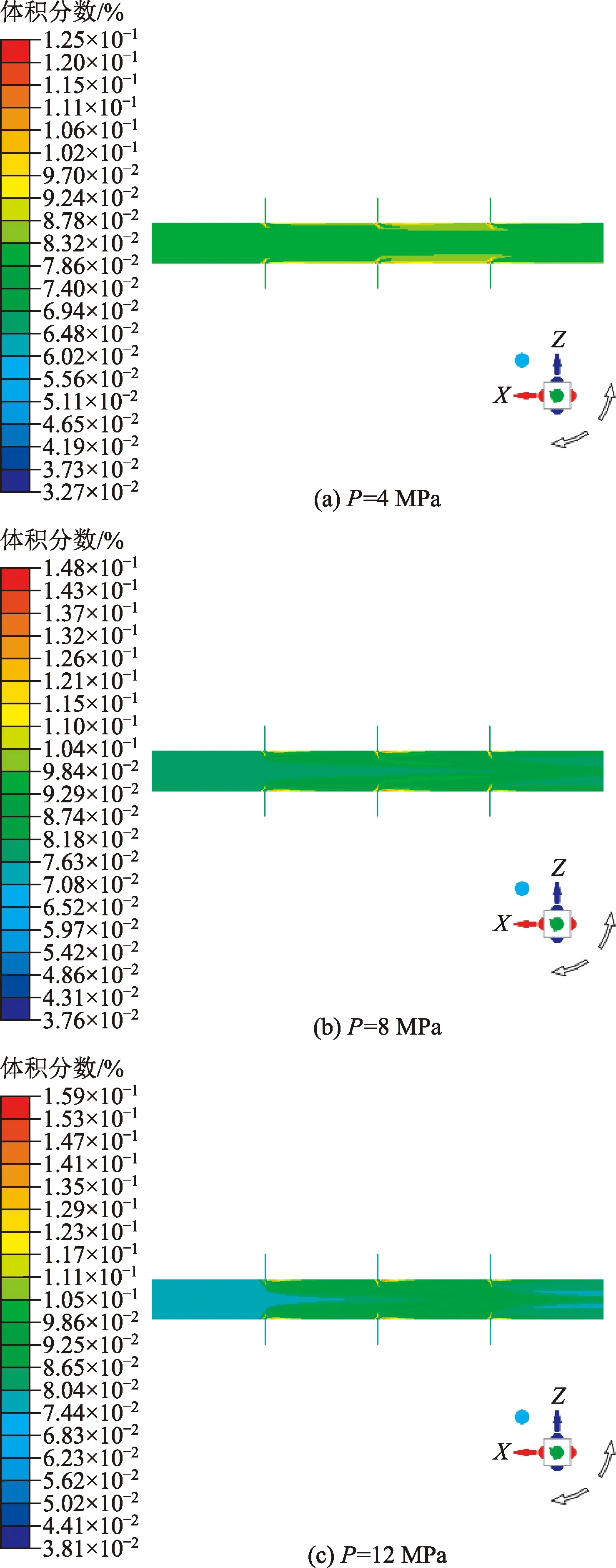
图5 固相体积分布Fig.5 Distribution of solid phase volume

随着油田的开发，地层中油藏压力不断降低，由速度分布曲线(图6)可以看出，随着油藏中的压力不断降低，井筒中流体速度曲线开始趋于平缓，并最终都呈现出下降趋势，出口速度都为0.36 m/s左右，但是当裂缝压力为14 MPa的时候，井口速度最大达到0.45 m/s，且随着裂缝压力的降低入口速度降低，当裂缝压力为4 MPa时，入口速度最低，为0.34 m/s，由速度分布曲线(图6)和速度分布云图(图7)可以看出，当裂缝压力为8 MPa时，入口速度为0.36 m/s，此时进出口速度差最小，最不利于砂砾的沉积。

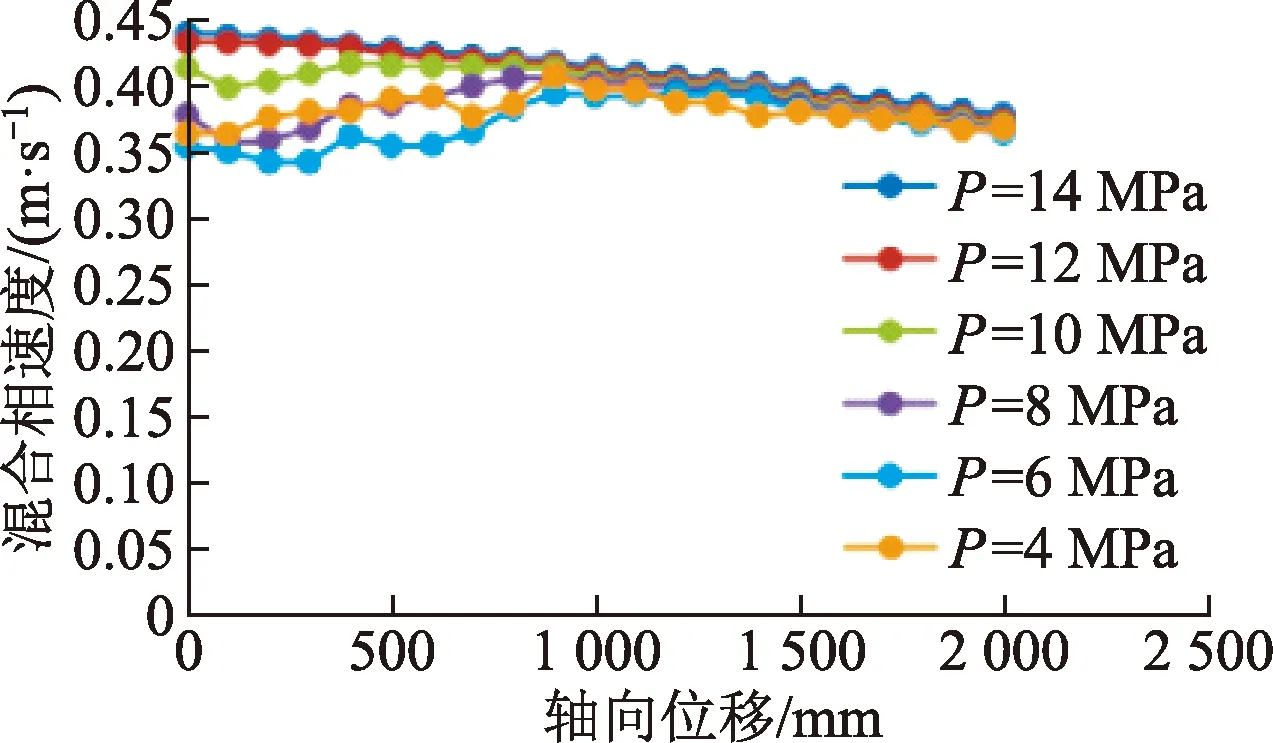
图6 速度分布曲线Fig.6 Velocity distribution curve

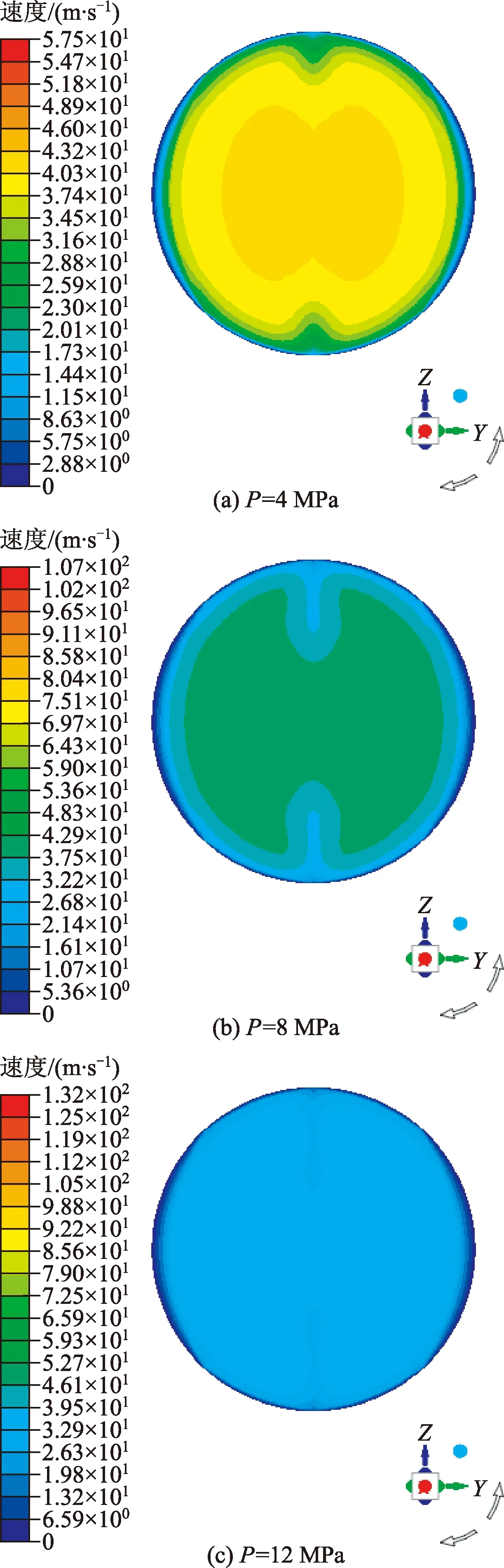
图7 裂缝压力速度分布云图Fig.7 Velocity distribution cloud diagram of fracture pressure

3.2 水平井井斜角

通过建立带有倾斜角度的水平井模型(模型a、模型b、模型c)来模拟不同井斜角对砂砾沉积的影响，分别设置井斜角α分别为90°、85°、80°，井筒入口速度v分别为0.4、0.6、0.8、1.0、1.2、1.4 m/s，裂缝入口速度v1分别为0.5、0.7、0.9、1.1、1.3、1.5 m/s 时，选取距入口1 200 mm处截面对比不同速度、不同井斜角所对应的固相体积分数。

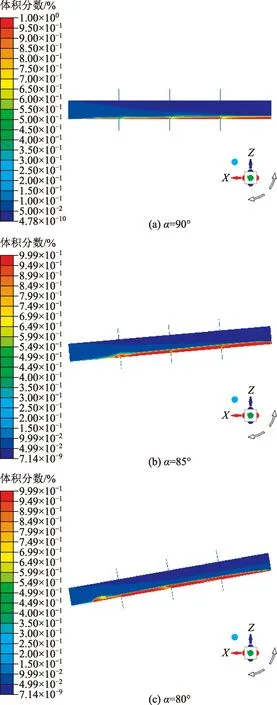
图8 整体流场固相体积分数云图Fig.8 A solid volume fraction cloud map of the whole flow field

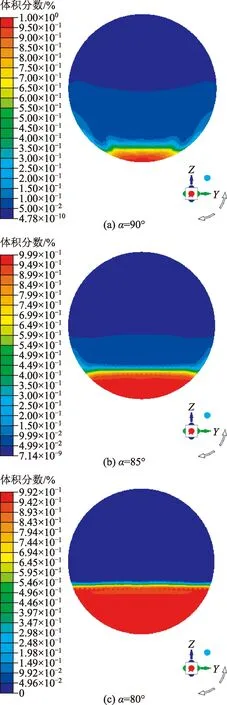
图9 v=0.8 m/s，v1=0.9 m/s 时固相体积分数云图Fig.9 Cloud diagram of solid phase volume fraction when v=0.8 m/s, v1=0.9 m/s

由图8、图9可以看出，当井斜角α由90°转变为85°、80°时，井筒内砂砾的沉积开始发生转变，当井斜角α为90°时，砂床沉积较为均匀，在入口附近开始沉积并且逐渐增厚，达到一定厚度之后开始趋于稳定；当井斜角α为85°、80°时，井筒内砂床形成趋势为先增厚再略微变薄然后再缓慢增厚。这是因为当井斜角变为85°、80°时，由于重力作用砂砾开始在入口处沉积，并且沉积的砂床干扰入口处的流体正常流入井筒，在达到一定厚度的时候，井筒内的流体在入口处形成涡流，于是在入口处形成厚度最大的砂床，并且在越过入口处最高砂床之后由于涡流的作用砂床厚度开始降低直至稳定。在进行对比相同入口速度、裂缝速度的情况下，不同井斜角所对应的固相体积分布云图之后可以看出，当井斜角为90°、井筒入口速度为0.8 m/s、裂缝速度为0.9 m/s时，井筒内固相体积分数为9.8%；井斜角为85°时相同情况下井筒内固相体积分数为18.6%；井斜角为80°时相同情况下井筒内固相体积分数为22.7%。

由图10可以看出，相同流速情况下，随着井斜角的增大固相所占百分比降低，相同井斜角的情况下随着流体速度的增加，固相所占百分比都呈现出下降的趋势，且井斜角越小，下降的趋势越大。

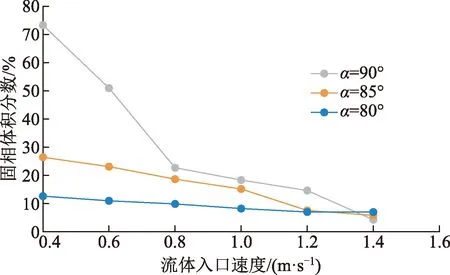
图10 固相体积分布曲线Fig.10 Distribution curve of solid phase volume

3.3 分段多簇压裂

体积压裂水平井，在体积压裂过程中采用多簇多段压裂，于是建立三簇三段压裂水平井简化模型(模型2)来模拟不同入口速度对砂床沉积的影响，井筒入口速度v分别为0.4、0.6、0.8、1.0、1.2、1.4 m/s，裂缝入口速度v1分别为0.5、0.7、0.9、1.1、1.3、1.5 m/s时，选取距入口1 200 mm处截面对比不同速度所对应的固相体积分数，并且与单缝压裂相同条件下砂床沉积情况进行对比分析，不同入口速度条件下固相分布云图如图11、图12所示。

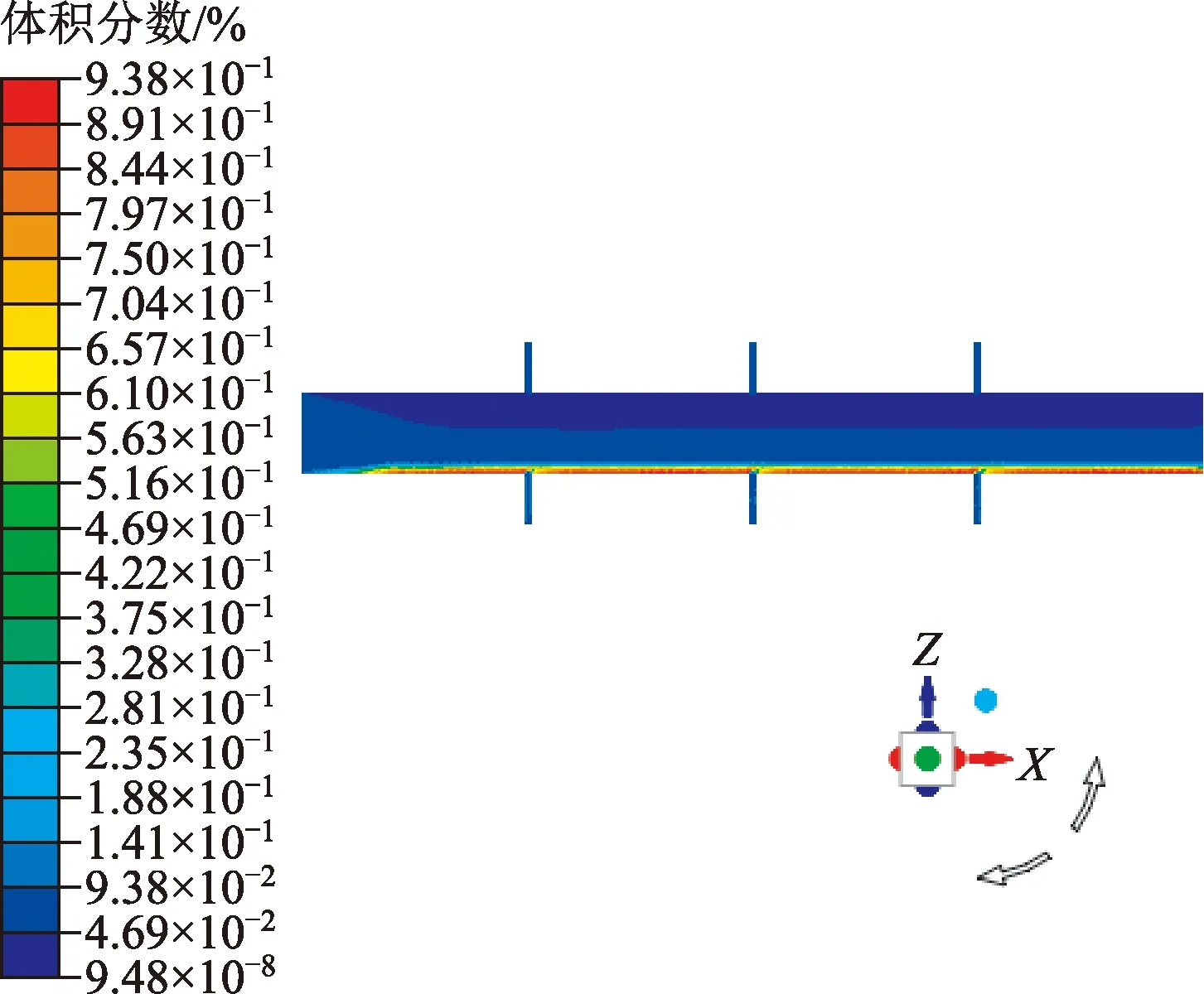
图11 多簇压裂整体流场固相分布云图Fig.11 Solid phase distribution cloud map of multi-cluster fracturing overall flow field

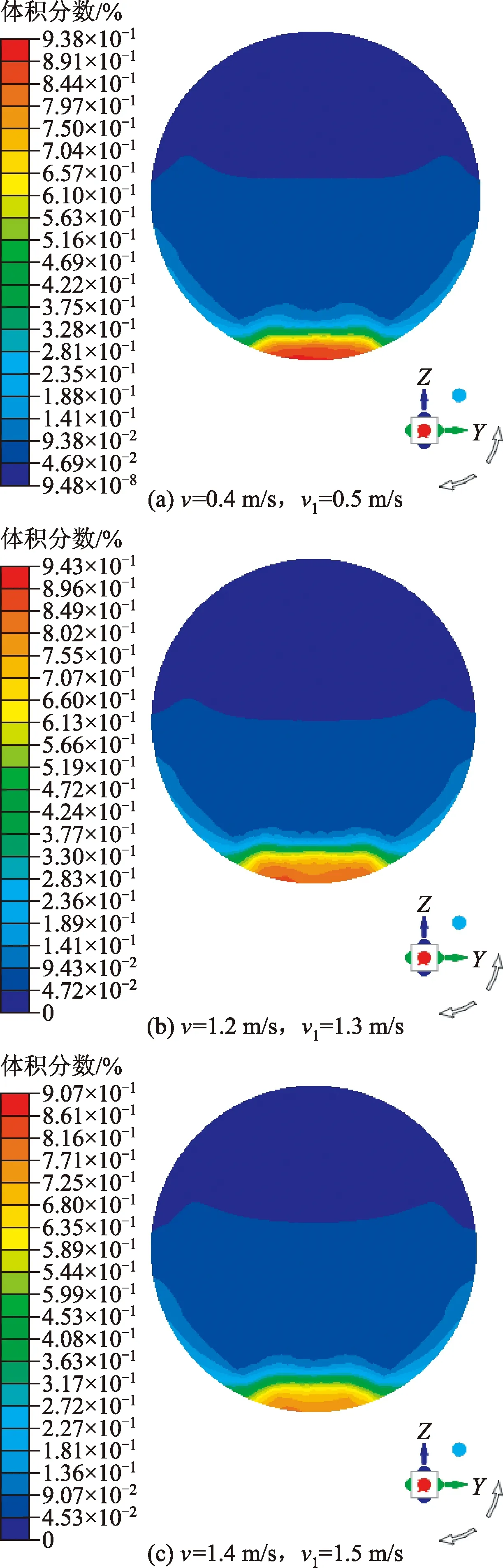
图12 多簇压裂时固相体积分布云图Fig.12 Cloud map of solid phase volume distribution during multicluster fracturing

当井筒内流体流速为0.4 m/s、裂缝内流体流速为0.5 m/s时，固相体积分数为12.3%，并且随着流体流速的升高，固相体积分数缓慢降低，直到井筒内流体流速上升1.2 m/s、裂缝内流体流速为1.3 m/s时，固相体积分数为6.3%，井筒内流体流速为1.4 m/s、裂缝内流体流速为1.5 m/s时固相体积分数为5.4%，此时，固相体积分数降低幅度减小并且趋于稳定。由多簇压裂时固相体积分布云图(图12)可以看出，随着流体流速的增大，砂床厚度逐渐降低，但相比于单缝压裂水平井并不十分明显，这是由于速度相同时，多簇压裂水平井较单缝压裂水平井流量大于是砂床形成厚度更低。

由固相体积分数随入口速度的变化曲线(图13)可以看出，单缝压裂水平井同多簇压裂水平井固相体积分数都随流体速度的增加呈现出相同的下降趋势，但是多簇压裂水平井明显较单缝压裂水平井固相体积分数大，这是由于单缝压裂水平井，流体速度相同时较多簇压裂水平井流量小以至于砂床形成较厚。

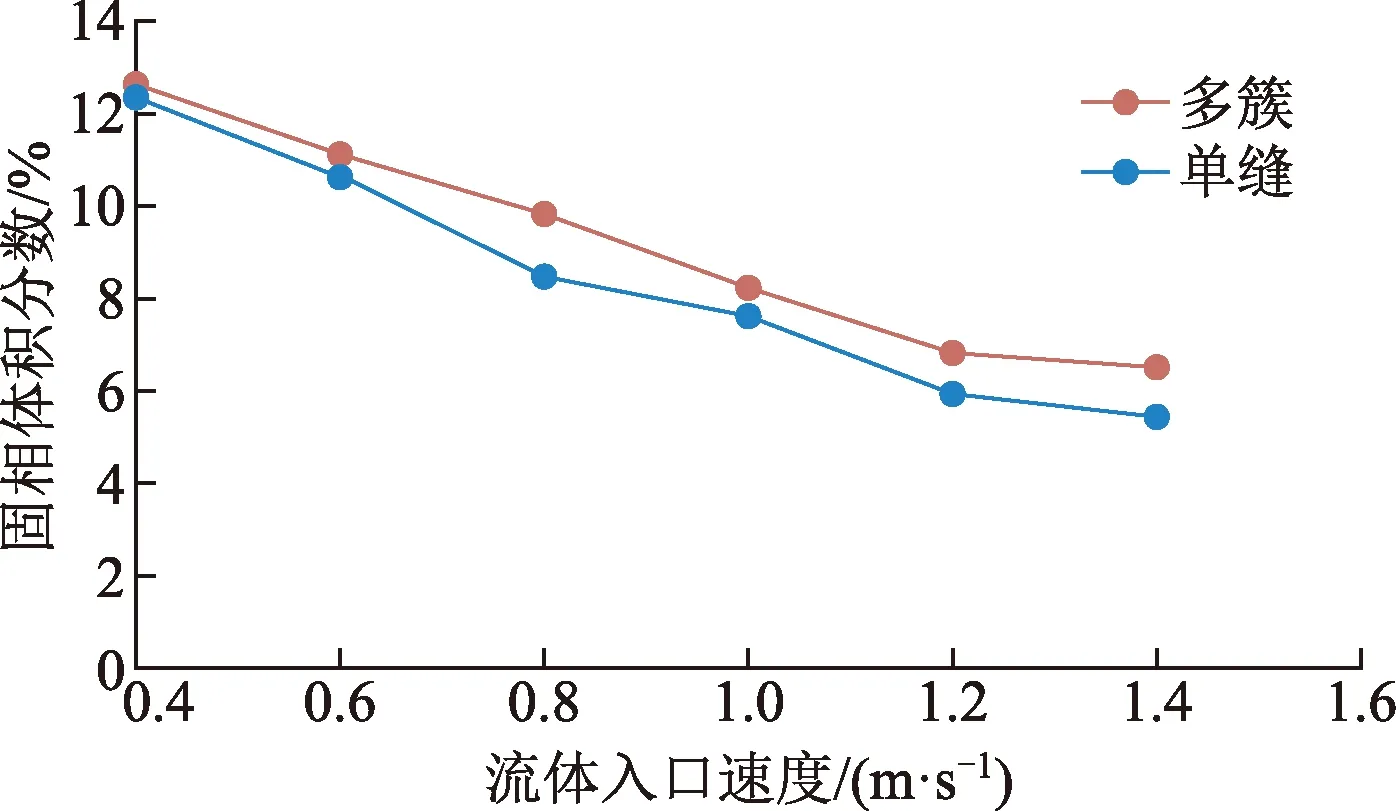
图13 固相体积分布曲线Fig.13 Solid phase volume distribution curve

4 结论

运用固液两相流、水平井体积压裂等理论分析，以及CFD数值模拟研究了在带有裂缝的条件下水平井携砂能力的影响因素，得到以下结论。

(1)体积压裂水平井不断开采过程中，随着油层压力的不断降低导致出砂量上升,通过模拟可以得到当压力为8 MPa的时候砂床形成厚度最低。

(2)单缝压裂水平井相比于多簇压裂水平井相同入口速度情况下由于单缝压裂水平井流量较小导致出砂问题比多簇压裂水平井严重，相同条件下多簇压裂水平井固相体积分数较单缝压裂水平井固相体积分数增加1%～3%。

(3)体积压裂水平井出砂随着井斜角的降低，出砂量增大，并且井斜角对体积压裂水平井的影响较大，井斜角90°时砂床主要堆积在出口附近，当井斜角为85°或者80°时从进口附近开始堆积，并且固相体积分数达到了50%以上，井斜角越小砂床厚度受流体速度影响越大。