多模式并联机构操作模式变换方法研究
2020-06-29单彦霞张建伟于靖军韩雪艳李仕华
单彦霞 张建伟 于靖军 韩雪艳 李仕华
(1.燕山大学机械工程学院, 秦皇岛 066004; 2.燕山大学里仁学院, 秦皇岛 066004;3.燕山大学河北省并联机器人与机电系统实验室, 秦皇岛 066004; 4.北京航空航天大学机器人研究所, 北京 100191)
0 引言
多模式并联机构(也称多操作模式机构)作为一种可重构并联机构受到了许多学者的关注[1]。多模式机构又称为运动分岔机构[2-4],其主要特性是在运动过程中通过约束奇异点改变运动特性,进而变换操作模式,进行变自由度的重构[5]。多模式机构可以利用较少的驱动器实现较多的操作模式,并且操作模式变换时不需要拆卸机构,具有变换时间少的优点[6]。
近年来,多模式机构的研究主要集中在构型综合和可重构分析。在构型综合方面,KONG等[7-8]根据变自由度支链提出了一种综合多模式机构的通用方法,并综合出了一系列多模式机构;方跃法团队[9-11]通过将含约束奇异特性的单环闭链与串联支链结合得到一类特殊的可重构混联支链,并综合出了一系列多模式机构。在可重构分析方面,文献[12-13]利用对偶四元数表示平台位姿,并结合运动学映射分析了SNU 3-UPU并联机构的操作模式;KONG等[14-15]则利用四元数来表示平台的姿态,对4自由度3-RER多模式机构和一种具有平面三自由度和3T1R自由度操作模式的变自由度机构进行了可重构分析。上述研究的机构可重构分析都是利用代数几何对机构的约束方程进行分析,只是约束方程建立的方法有所不同。
多模式机构在构型综合以及可重构分析方面已经得到了广泛的研究,但是关于多模式机构的驱动器布置方式以及操作模式间变换的研究并不多见。驱动副数量影响着可以实现的操作模式数量,驱动副的选取也会对机构奇异的特性产生影响,机构中的奇异点往往是自由度切换点,必须考虑如何正确过渡[16]。KONG等[7]提到,驱动关节的最佳选择和从一种操作模式切换到另一种操作模式的方法仍然是开放问题。CHABLAT等[17]给出了3-PRPiR机构不同操作模式之间转换的方法,并通过可锁运动副实现多操作模式。刘伟等[18]综合了一种新的多模式机构,并通过在支链上增加辅助驱动副,实现并联机构运动模式之间的变换。
现有的多模式机构模式间变换方法还存在对通过约束奇异实现多模式变换的适用性问题。本文结合整体运动/力约束性能指标[19]提出一种实现多模式机构操作模式间变换的方法。该方法采用TCI(Total constraint index)确定机构的近似约束奇异空间,只在该空间内启动辅助驱动,以实现不同操作模式间的平稳变换,为多模式机构的应用奠定理论基础。
1 机构可重构分析
机构处于约束奇异时的位形称为变换位形。操作模式为描述动平台运动类型的连续位姿集合[7],也可看作是被约束奇异曲面分割的工作空间的子空间[5]。可重构分析可以得到多模式机构的各种操作模式及操作模式间的变换位形。
使用对偶四元数能更系统地描述动平台的位姿[20],对偶四元数可以表示为
Q=x0+x1i+x2j+x3k+ε(y0+y1i+y2j+y3k)
(1)
式中ε——对偶因子,满足ε≠0且ε2=0
其系数满足
x0y0+x1y1+x2y2+x3y3=0
(2)
(3)
利用式(3),任意倍数的λQ(λ≠0)均可转换为Q,因此满足式(3)的Q可一一映射为7维射影空间PR7中的点(x0,x1,x2,x3,y0,y1,y2,y3),式(2)可以看作为PR7中的6维二次曲面S,又称为Study二次曲面[21],该6维曲面上的点与刚体在3维空间中的位姿一一对应,齐次变换矩阵M表示为
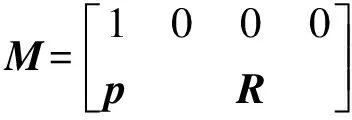
(4)
式中R——旋转矩阵p——位移
如图1所示,通过上述映射,并联机构的工作空间就可以描述为Study二次曲面上的曲线,曲线p1、p2分别表示操作模式M1、M2的工作空间,并交于变换位形点T,通过位置反解得到的函数f可映射到两种模式的关节空间q1、q2。
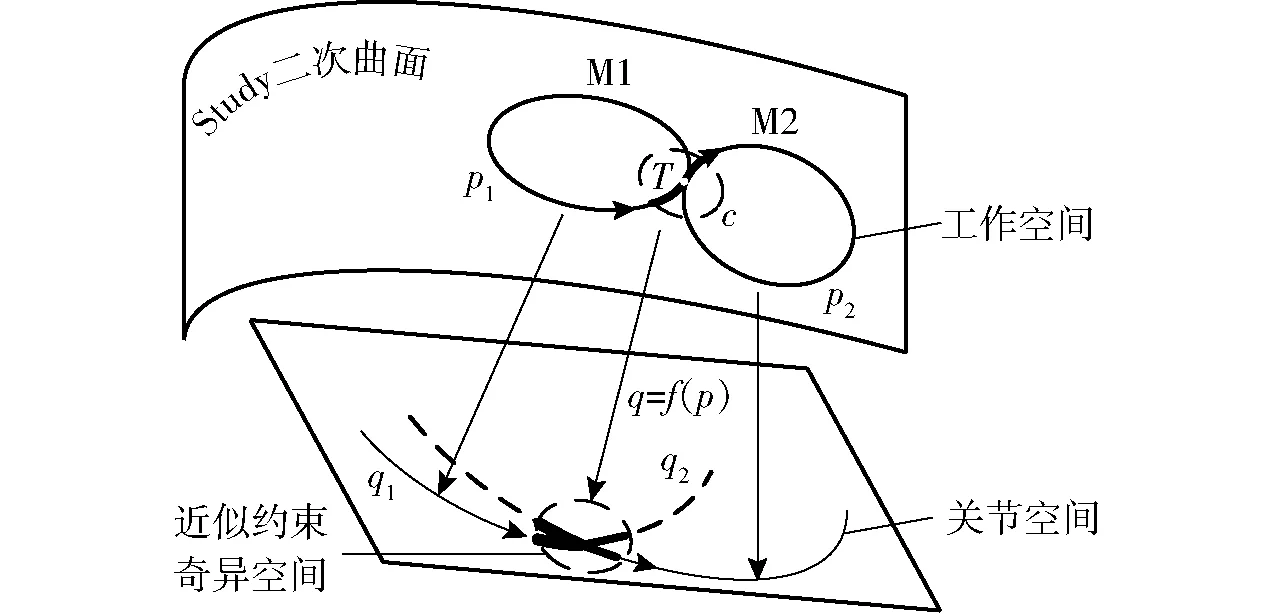
图1 多模式机构工作空间与关节空间的映射Fig.1 Mapping of workspace and joint space of multi-mode mechanism
1.1 操作模式分析
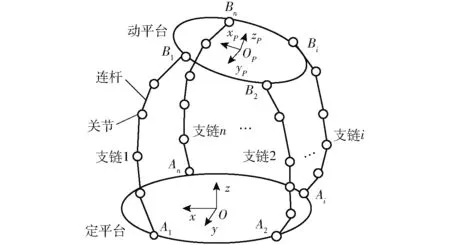
图2 多模式并联机构结构示意图Fig.2 Structural diagram of multi-mode parallel mechanism
数学上操作模式是机构约束方程的所有相同的不可约正维解的集合,可通过建立多项式约束方程,进行准素分解得到[22]。如图2所示,包含n个支链的n自由度非冗余并联机构,若假设动平台的位姿在PR7的坐标为(x0,x1,x2,x3,y0,y1,y2,y3),则可以建立3类约束方程求解动平台的位姿:
第1类为Study二次曲面方程g1和归一化方程g2,即式(2)和式(3)。
第2类为关节参数约束方程gi,描述动平台位姿与驱动关节参数之间的关系
gi(t,x)=0 (i=3,4,…,n+2)
(5)
其中t=(t1,t2,…,tn)
x=(x0,x1,x2,x3,y0,y1,y2,y3)
式中t——机构驱动关节输入参数
x——动平台位姿
第3类为几何结构约束方程gj,用于描述支链关节对动平台运动的约束限制
gj(x)=0 (j=n+3,n+4,…,2n+2)
(6)
利用代数几何理论[23]将式(2)、(3)、(5)、(6)组成多项式理想I=〈g1,g2,…,g2n+2〉,先对不含常数项的方程组成的多项式理想J=〈g1,gn+3,gn+4,…,g2n+2〉进行分析,通过数学软件Maple中多项式理想库PolynomialIdeals的PrimeDecomposition函数对其进行准素分解
(7)
确定理想I的代数簇为
(8)
其中Ki=Ji∪〈g2,g3,…,gn+2〉
代数簇V(I)可以理解为理想I中方程的公共零点,即该机构整个工作空间,而V(Ki)正是约束奇异曲面分割工作空间后的子空间,即操作模式。每个理想Ki对应一种操作模式Mi,将操作模式Mi对应理想的代数簇V(Ki)代入式(4)可得到这种操作模式的齐次变换矩阵M,通过分析矩阵M可得机构在操作模式Mi时的运动类型。
1.2 变换位形分析
机构的变换位形可通过对各操作模式求交集获得,操作模式Mi和操作模式Mj的变换位形i∧j的代数簇为
i∧j=V(Ki)∪V(Kj)
(9)
如果交集不为空则该交集为操作模式Mi和操作模式Mj的变换位形,此时机构处于约束奇异状态。
2 多模式机构驱动空间求解
并联机构驱动布置方式会影响机构的奇异性、刚度和运动/力传递特性等,通常会优先选择基座副或靠近基座的运动副、移动副作为驱动副[24-25]。将驱动副进行排列组合,构成基础驱动空间S0。在操作模式Mi下,基础驱动空间S0中所有合理的驱动组合Acta,称为操作模式Mi的驱动空间Si。
变换位形的驱动空间是指既可以摆脱奇异位形又可控地进行两种操作模式间变换的合理驱动组合。为实现Mi和Mj两种操作模式,驱动的选择须同时满足2种操作模式的驱动要求,且能够消除变换位形i∧j的约束奇异。因此,变换位形的驱动空间Sij为
Sij={Acta∩Actb|Acta∈Si,Actb∈Sj}
(10)
即可得到变换位形下的辅助驱动组合Actc。
支链内的约束奇异产生局部自由度时,需要添加额外的驱动来消除该局部自由度,使机构可以从一种操作模式变换到另一种操作模式。
将满足机构所有操作模式及变换位形要求的驱动组合构成机构的驱动空间,并从中选出最优的驱动组合。驱动组合的优选原则为:①尽量选择机座副、移动副作为驱动副。②应优先选择最少驱动副数量的驱动组合。③选择的驱动副在机构中的位置应尽量对称。
3 操作模式变换
3.1 近似约束奇异空间
多模式机构在奇异位形及其附近会失去控制。文献[19]提出了整体运动/力约束特性指标TCI,用于评价并联机构距离约束奇异位形,范围为[0,1],0表示机构处于约束奇异位形。其计算方法如下:
计算输入端运动/力约束特性指标ICI(Input constraint index)
(11)
式中 $Cij——第i支链中第j个约束螺旋
$Rij——第i支链中第j个受限运动螺旋
计算输出端运动/力约束特性指标OCI(Output constraint index)
(12)
式中 $Ci——动平台受到的第i个约束螺旋
Δ$Oi——第i个虚拟输出螺旋
整体运动/力约束特性指标TCI为
(13)
机构在约束奇异位形附近时约束性能较差,本文以κ=0.3为阈值,即图1中的虚线c,将约束奇异位形附近κ<0.3的工作空间称为近似约束奇异空间。
3.2 操作模式变换的过程
图1中关节空间中的实线表示主动输入参数,虚线表示被动关节参数。在近似约束奇异空间内,可采用冗余驱动的方法实现操作模式间的平稳变换。操作模式间的变换可分为3个阶段:
(1)操作模式Mi进入近似约束奇异空间时,如图1中关节空间中的粗实线所示,启动辅助驱动组合Actc,操作模式Mi不变,机构按Mi的反解驱动。
(2)到达变换位形时,机构从操作模式Mi变换为操作模式Mj,机构按操作模式Mj的反解驱动。
(3)操作模式Mj离开近似约束奇异空间时,关闭辅助驱动组合Actc。
机构从操作模式Mi变换到操作模式Mj的流程如图3所示。

图3 操作模式变换流程图Fig.3 Flow chart of operation mode transformation
4 实例分析
以SNU 3-UPU机构的两种操作模式变换为例,分析其变换过程。
4.1 可重构分析
SNU 3-UPU机构由动平台、定平台以及3条完全相同的UPU支链构成,如图4所示。每个U副由2个相互垂直相交的转动副构成,其中与平台相连的转动副称为U副第一转动副U1,与P副相连的转动副称为U副第二转动副U2。平台上的U副均匀布置在等边三角形顶点,U副中的第一转动副平行于平台,且指向平台圆心。定平台外心圆半径为r1,动平台外心圆半径为r2,支链的两个U副Ai与Bi之间的距离为di。
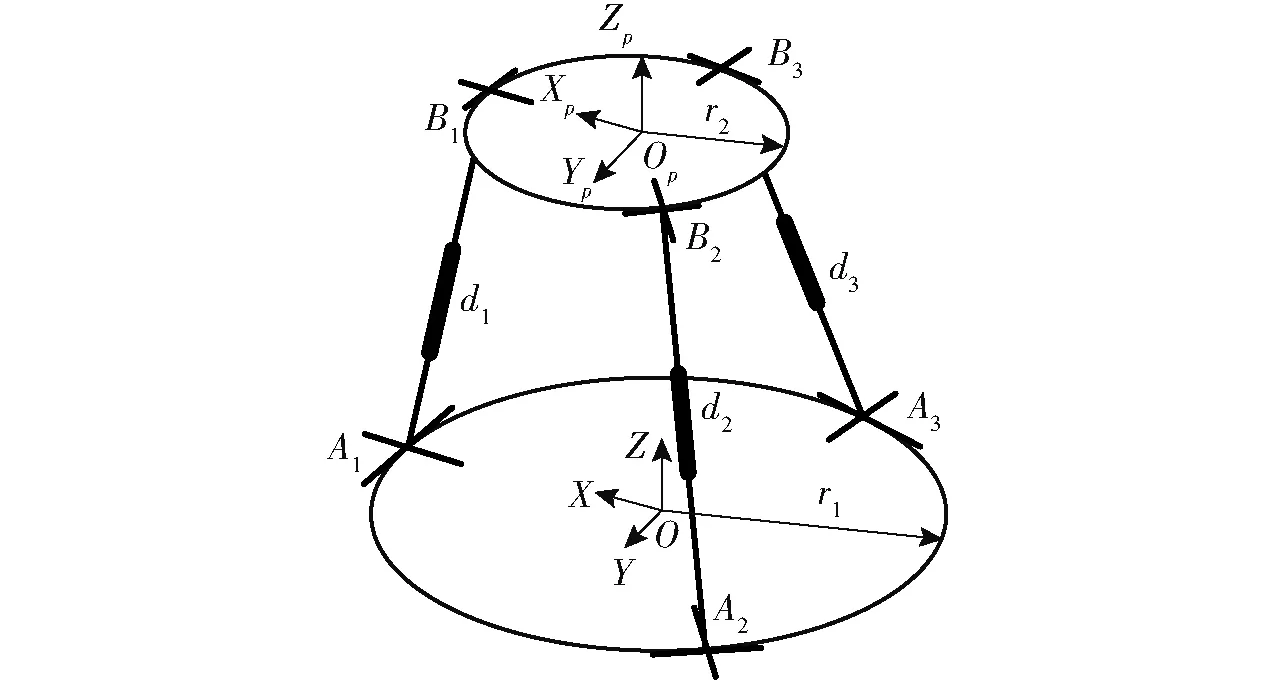
图4 SNU 3-UPU并联机构简图Fig.4 Diagram of SNU 3-UPU parallel mechanism
文献[13]对SNU 3-UPU并联机构进行可重构分析并得到了9种操作模式,其中2种复数理想对应的操作模式是3T模式的特例,其余7种操作模式如表1所示。
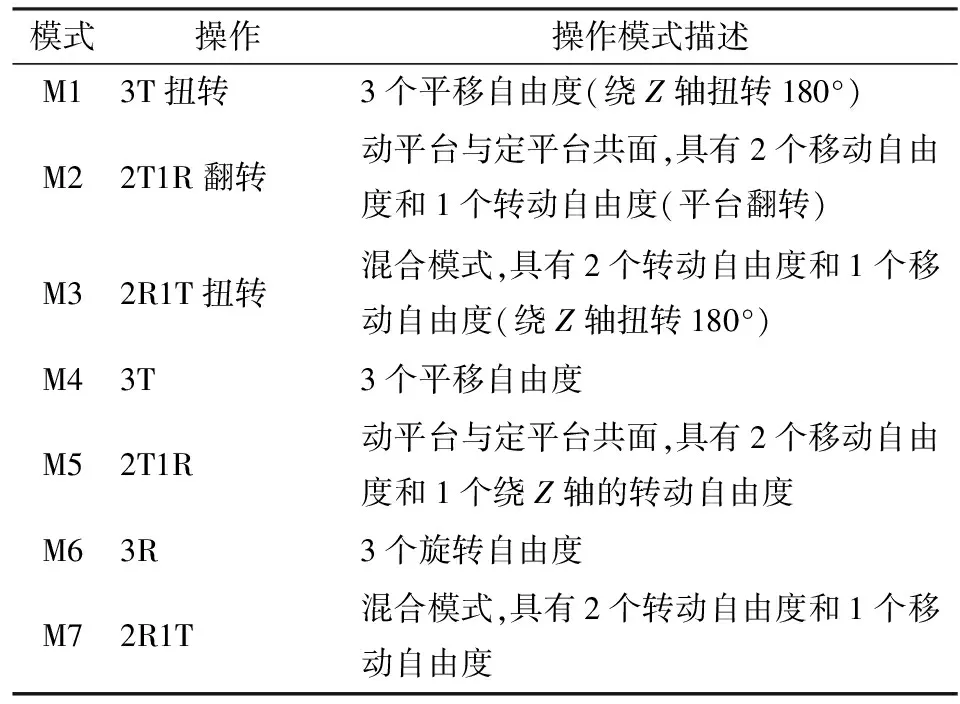
表1 操作模式Tab.1 Operation configurations
各操作模式对应的机构一般位形如图5所示。由图5可以看出,在M1、M2、M3操作模式下会出现P副超出其工作范围或运动副间产生干涉的问题。因此分析其他4种操作模式间的变换,得到4种变换位形,如表2所示。
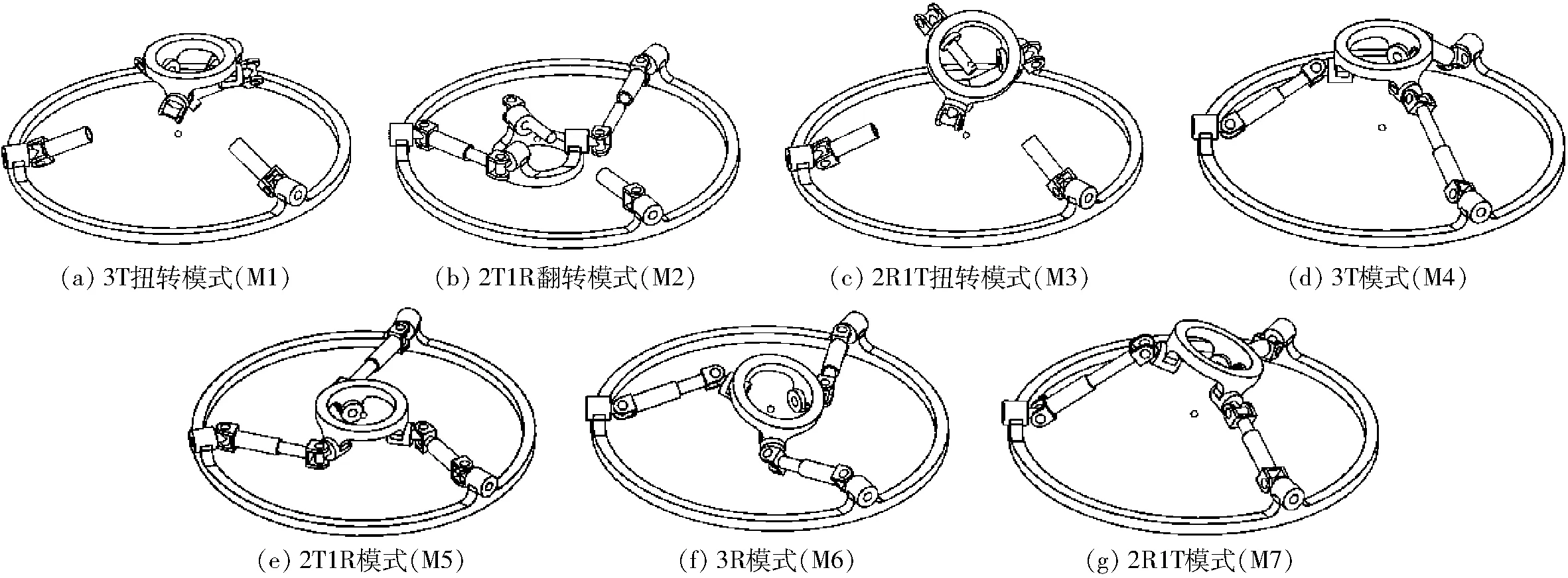
图5 SNU 3-UPU机构的操作模式Fig.5 Operation modes of SNU 3-UPU mechanism
以3T操作模式和2T1R操作模式之间的变换为例,说明确定合理驱动及实现模式变换的过程。
4.2 SNU 3-UPU机构驱动空间分析
4.2.1操作模式的驱动空间
根据第2节的输入选取原则,选取各支链机架上的U副第一转动副U1,第二转动副U2以及移动副P为驱动副,且各支链中仅选取一个驱动副,经排列组合可得到机构的基础驱动空间S0,共10种驱动组合方式,如表3所示。

表2 变换位形Tab.2 Transformation configurations

表3 SNU 3-UPU的10种驱动组合Tab.3 10 Actuation combination of SNU 3-UPU
注:带下划线的运动副为选取的驱动副。
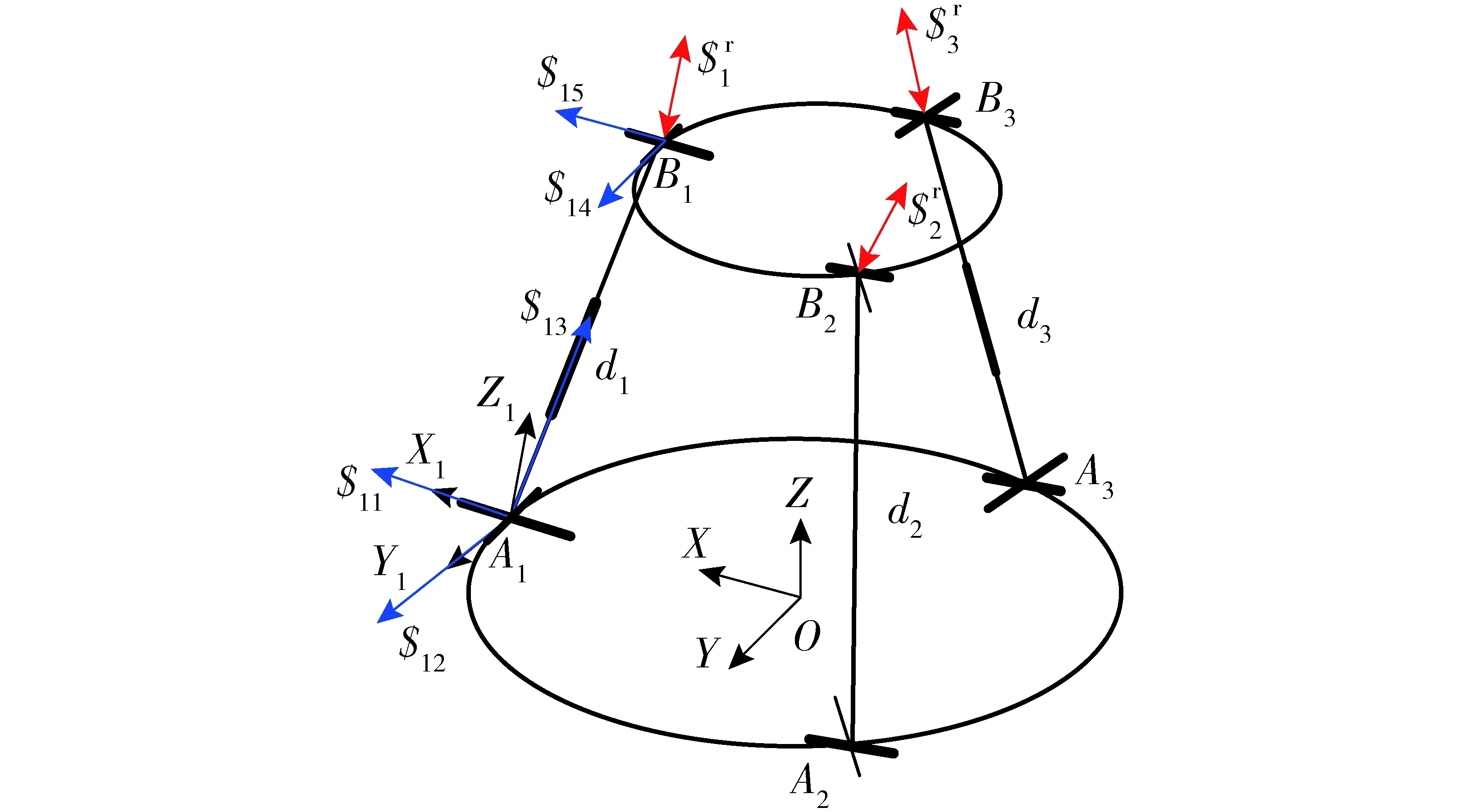
图6 3T模式的螺旋系分析Fig.6 Screw system analysis of 3T mode
操作模式M4和M5的驱动空间为S4、S5。模式M4有3个平移自由度,建立支链坐标系A1X1Y1Z1,如图6所示。X1轴与第一转动副U1轴线重合,Y1轴与第二转动副U2轴线重合,Z1轴按右手法则确定。
根据螺旋理论,支链约束螺旋$i(i=1,2,3)为平行于Zi轴的约束力偶。驱动螺旋与非驱动副运动副旋量的互易积为0,且与所有约束力线性无关。
选择不同的驱动副对应的驱动螺旋及几何描述如表4所示。

表4 3T模式的驱动螺旋Tab.4 Actuation combinations of 3T operation mode
由表4可知,该操作模式下合理的驱动空间为S4={Act 1, Act 2, Act 3, Act 4, Act 5, Act 6, Act 7, Act 8, Act 9, Act 10},即表3中的10种驱动组合均满足该操作模式的驱动要求。
同理对模式M5进行分析,其支链螺旋系以及约束螺旋系如图7所示。对表4所列驱动螺旋进行线性相关性分析可知,该操作模式合理的驱动空间为S5={Act 7, Act 8, Act 9, Act 10},即表3中的4种驱动组合满足该操作模式的驱动要求。
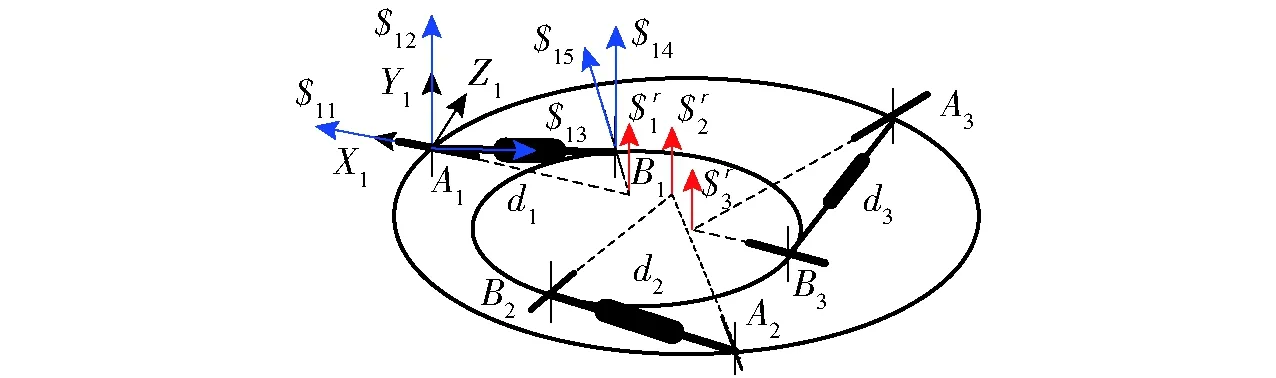
图7 2T1R模式的螺旋系分析Fig.7 Screw system analysis of 2T1R mode
4.2.2变换位形的驱动空间

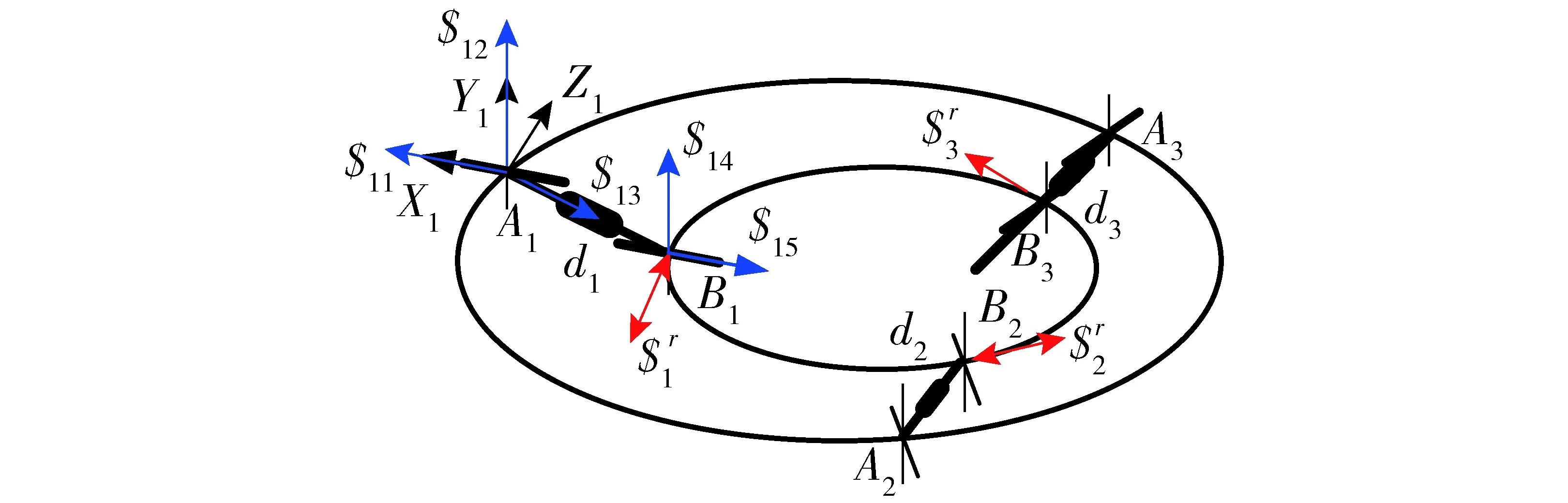
图8 变换位形的螺旋系分析Fig.8 Screw system analysis of transformation configuration
根据式(12)可得该变换位形的驱动空间为
(14)
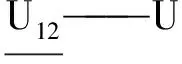
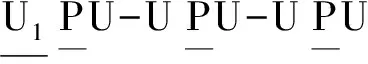
4.3 3T模式与2T1R模式间变换
4.3.1近似约束奇异空间

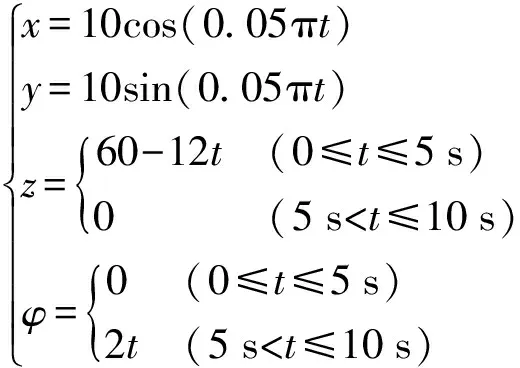
(15)
式中φ——绕Z轴的转角,(°)
对应位姿随时间的变化曲线如图9所示。
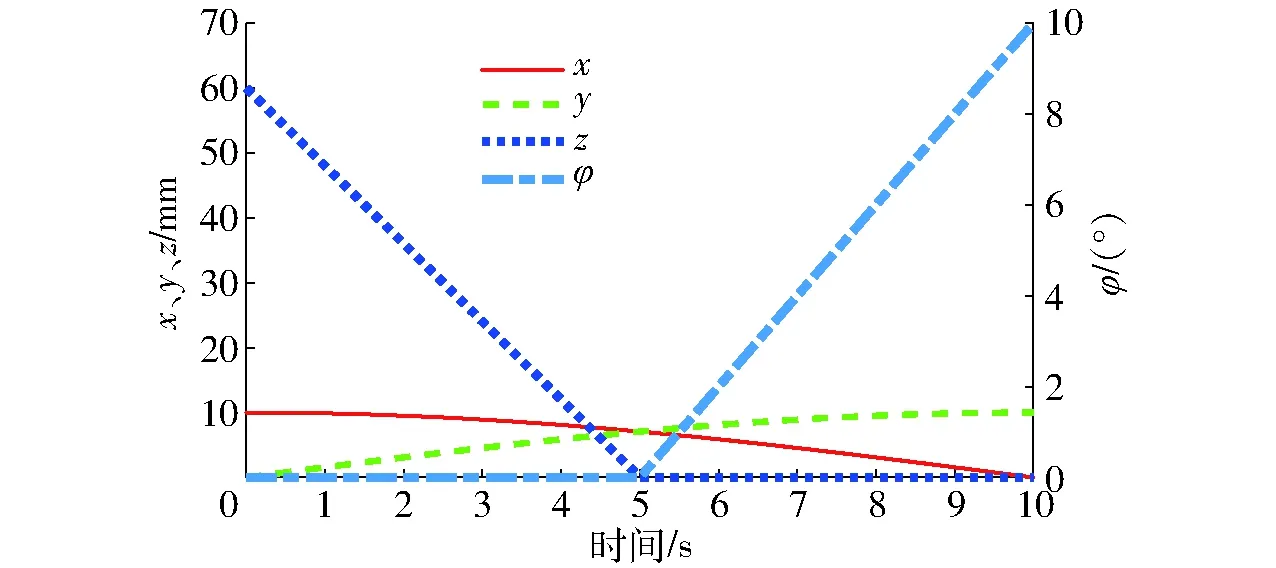
图9 SNU 3-UPU机构动平台位姿变化曲线Fig.9 Position and pose change curves of moving platform of SNU 3-UPU
分析3T模式与2T1R模式的近似约束奇异空间。在3T模式下(图6),3-UPU机构存在3个约束力偶旋量$Ci和3个输入端单位受限运动旋量$Ri,分别为
(16)
式中sij——与螺旋$ij指向相同的矢量
bi——固定坐标系原点O到Bi的矢量
将式(16)代入式(13)可得机构在不同动平台高度时XY平面的TCI指标性能图谱,如图10所示。

图10 SNU 3-UPU机构在3T模式时的TCI指标性能图谱Fig.10 TCI performance atlases of SNU 3-UPU mechanism in 3T mode
分析2T1R模式的近似约束奇异空间(图7)。3-UPU机构存在3个约束力线矢旋量$Ci和3个输入端单位受限运动旋量$Ri,分别为
(17)
将式(17)代入式(13)可得机构在动平台绕Z轴不同转角时XY平面上的TCI指标性能图谱,如图11所示。
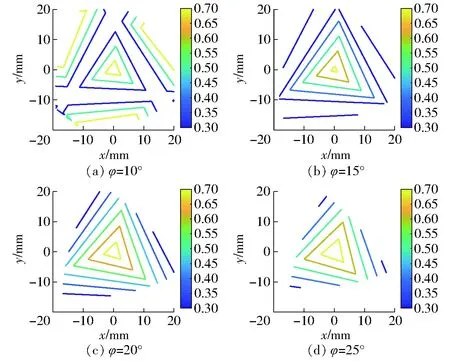
图11 SNU 3-UPU机构在2T1R模式时的TCI指标性能图谱Fig.11 TCI performance atlases of SNU 3-UPU mechanism in 2T1R mode
机构在3T和2T1R操作模式下沿轨迹运动时的TCI指标变化曲线,如图12所示。机构在3.48 s时到达近似约束奇异空间,由式(15)可得,此时动平台中心点在基坐标系中的位置为(8.54, 5.19, 6.08)mm;机构在t=5 s时TCI指标值为0,机构处于奇异位形;机构在5.36 s时离开近似约束奇异空间,此时动平台中心点在基坐标系中的位置为(6.66, 7.45, 0)mm,绕Z轴的转角φ为19.30°。
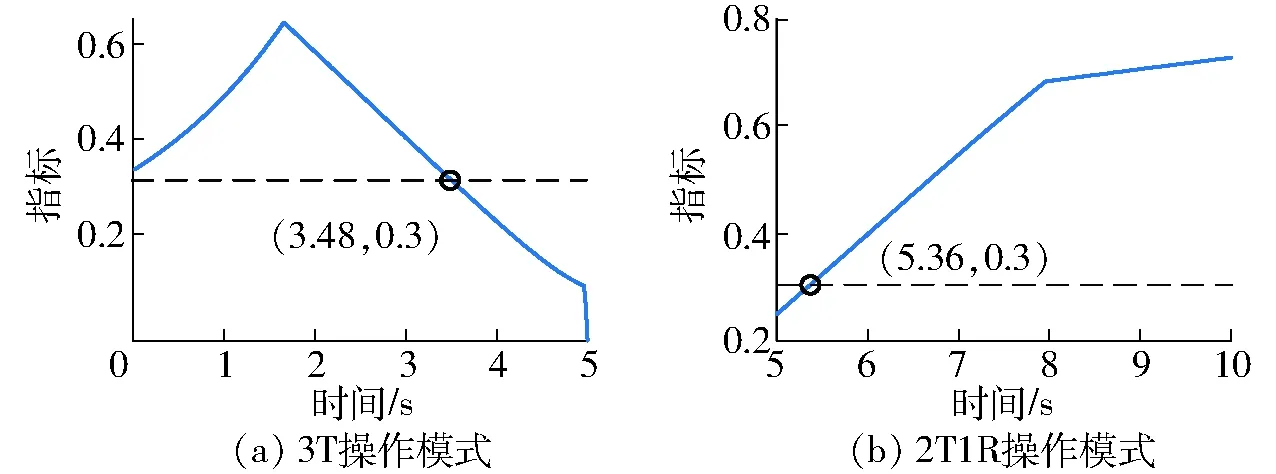
图12 SNU 3-UPU机构在沿轨迹运动时的TCI指标变化曲线Fig.12 TCI change curves of SNU 3-UPU mechanism moving along trajectory
4.3.2模式间变换
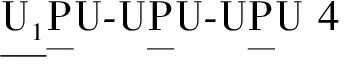
3T模式机构的位置反解为
(18)
2T1R模式机构的位置反解为
(19)
模式变换时驱动副输入曲线如图13所示,θ1为辅助驱动启动后的转角,θ2为辅助驱动关闭后的转角。在t为0~3.48 s时,机构处于3T模式,输入式(18)中d1、d2、d3位移进行驱动;在t=3.48 s时,进入近似约束奇异空间(图中黄色区域),启动辅助驱动,输入参数为θ1=atan2(y,z);在t=5 s时,到达变换位形,输入式(19)中d1、d2、d3位移进行驱动,辅助驱动的输入参数变为θ2=90°;保持辅助驱动输入参数为θ2=90°不变,直到t=5.36 s离开近似约束奇异空间,关闭辅助驱动。
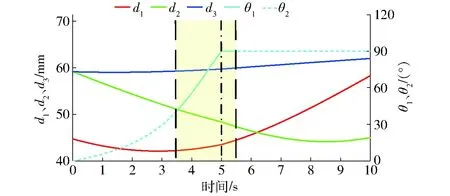
图13 3T模式与2T1R模式之间模式变换时的输入曲线Fig.13 Input curves transforming between 3T mode and 2T1R mode
4.4 仿真分析
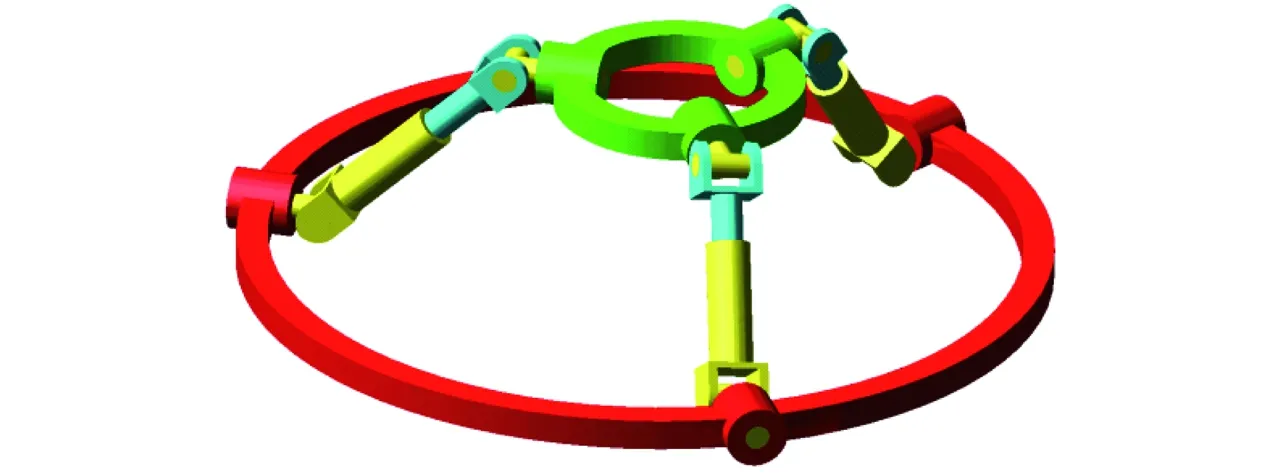
图14 SNU 3-UPU机构的仿真模型Fig.14 Simulation mode of SNU 3-UPU mechanism
建立SNU 3-UPU机构的仿真模型,如图14所示,动平台U副中心所在圆的半径为50 mm,定平台U副中心所在圆的半径为100 mm。导入ADAMS中,并按4.3节分析结果设置驱动副参数。
动平台X、Y、Z方向的位移和Z轴转角随时间变化的曲线如图15所示。由图15可知,与预定的运动轨迹图9一致,证明按照该方法驱动可以实现SNU 3-UPU机构3T操作模式与2T1R操作模式之间的平稳变换。
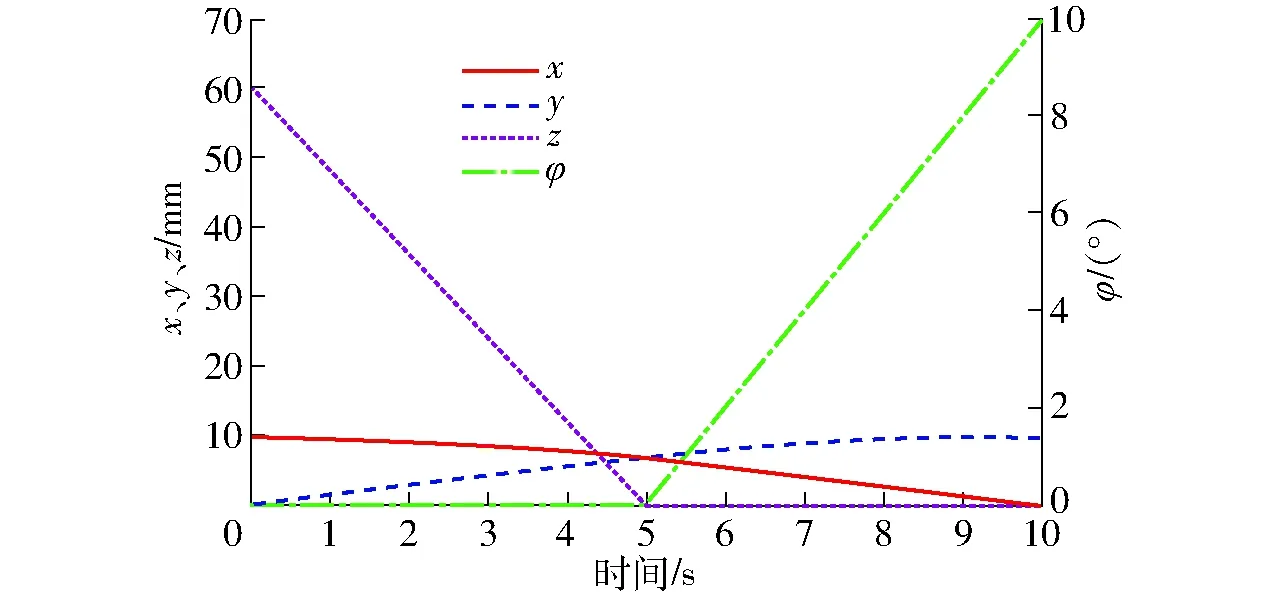
图15 SNU 3-UPU机构动平台位姿仿真变化曲线Fig.15 Position and pose simulation change curves of moving platform of SNU 3-UPU
5 结论
(1)提出了一种多模式并联机构的操作模式间变换方法。该方法基于整体运动/力约束特性指标TCI定义近似约束奇异空间,在该空间内通过添加辅助驱动的方式,实现操作模式之间的平稳变换。
(2)针对提出的方法,制定了不同操作模式间变换的流程,确定了驱动组合的优选原则,得到了合理的辅助驱动,并优选出机构的驱动空间。
(3)以SNU 3-UPU多模式并联机构为研究对象,进行了可重构分析,得到7种操作模式和4种变换位形,实现了3T操作模式和2T1R操作模式间的平稳变换。
