螺旋桨低频振动声辐射特性研究——水母模态

吴崇建，王春旭*，陈志刚，杜堃，雷智洋

1 中国舰船研究设计中心，湖北 武汉430064

2 船舶振动噪声重点实验室，湖北 武汉430064

0 引 言

随着机械噪声的持续降低［1-2］，舰船推进系统噪声凸显，成为舰船主要的噪声源，并呈现出低频宽带、低频线谱突出的特点［3］。推进系统噪声控制涉及的要素较多，如螺旋桨、轴系、船体结构、艉部线型、操纵面等，噪声机理复杂，涉及多学科与多物理场耦合，噪声控制难度大。

螺旋桨是舰船最典型的推进器，也是推进系统振动声辐射最主要的激励源和辐射源。螺旋桨噪声理论将噪声主要成分划分为了空化噪声、唱音、中高频噪声和低频噪声，其中低频噪声又可细分为低频宽带噪声和离散谱噪声［4-5］。在进行螺旋桨声学研究时，一般将桨叶当作刚体处理，而与桨叶弹性有关的振动声辐射主要是“唱音”，其机理是桨叶随边的局部模态与该处小尺度规则涡列结构的自激振动，该噪声频率相对较高［6］。螺旋桨低频噪声由其工作在舰船尾部非均匀、非定常伴流场中的非定常激振力产生，一方面，直接辐射声；另一方面，激励推进轴系、船体结构振动辐射声，并成为推进系统噪声的主要成因［7-8］。

在前期研究基础上，我们在2011～2012 年将一种量级突出的低频窄带谱辐射噪声成因与螺旋桨进行了关联。与传统的螺旋桨低频噪声特征不同，深入的理论分析和试验验证证明该特征谱由螺旋桨同相模态产生，将该模态命名为“水母模态”，而由该模态激发引起的声辐射则称为“水母效应”。2015～2017 年，又连续3 次在行业会上对噪声成分的特征、机理进行了阐释和补充。

本文将基于精细化有限元分析，揭示螺旋桨的低频模态特征，然后引用循环对称结构动力学理论对其动力学特征进行理论归纳。

1 螺旋桨低频模态特性精细化数值分析

1.1 对象及数值模型

为了说明螺旋桨的低频模态特征，选取图1所示的意大利船模水池E1619 螺旋桨作为分析对象。该桨是一个7 叶大侧斜螺旋桨，直径0.485 m，盘面比0.608。

螺旋桨为中心对称结构。为减小数值模型对计算结果的影响，数值模型须尽量保证对称性。取整个桨的1/7 几何结构，按照全六面体精细化网格划分，然后通过圆周阵列得到完全循环对称的计算模型。为适应螺旋桨复杂扭曲的外形，提高计算精度，增加了网格量，并应用了二次单元。有限元计算模型如图1 所示。分析边界取为自由边界，其他计算参数设置：材料密度ρ=8 000 kg/m3，杨氏模量E=1.3×1010Pa，螺旋桨模型重量为9.231 kg。

图1 7 叶螺旋桨精细化有限元计算模型Fig.1 The refined FE calculation model of a 7-blade propeller

1.2 空气介质中螺旋桨低频模态特性

1.2.1 7 叶螺旋桨模态特性

基于ANSYS 软件，计算得到空气介质中7 叶螺旋桨的模态频率如表1 所示。螺旋桨的低频模态呈现明显的分组特征，每组7 个模态。在第1 组模态中，每个桨叶振型为其第1 阶弯曲模态振型，组内不同模态桨叶间相位关系不同；在第2 组模态中，每个桨叶振型为其第2 阶模态振型，组内不同模态桨叶间相位关系不同。同组内的7 个模态频率相近，不同组间的模态频率差别较大。

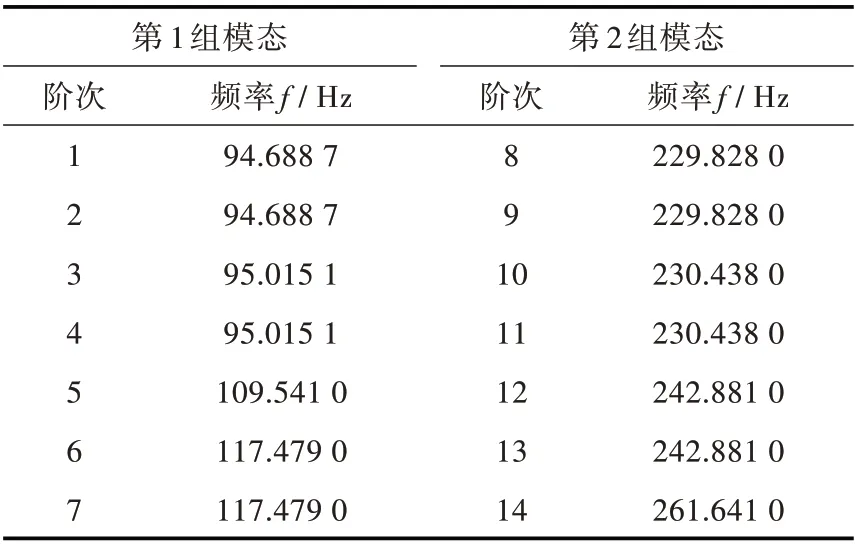
表1 7 叶螺旋桨弹性模态频率对比Table 1 The elastic modal frequency of a 7-blade propeller

进一步观察组内模态频率和振型特征，发现呈明显的单频和重频特征。7 个模态实际上只有4 个模态频率，其中，有3 个模态频率各自对应2个模态振型，属重频模态；1 个模态频率对应1 个振型，属单频模态。

为进一步说明单频和重频模态的振型特征，给出了其振型图，如图2 所示。用N 和P 分别表征同一瞬间桨叶振动沿轴线向前与向后的振动形态。由图可以看出，7 叶螺旋桨的模态振型按照模态频率分为了4 组，其中单频模态振型记为NNNNNNN，即7 个桨叶同相位振动，振型形似水母运动，故命名为“水母模态”。其他3 组为重频模态，其振型分别为NPNPNPN（PNPNPNP），NNPPNNP（PPNNPPN）和NNNPPPN（PPPNNNP），两两正交。另外还可以看出，3 组重频模态的振型全部为（3，4）组合，即3 个桨叶振动与另外4 个桨叶振动反相，不存在（1，6）组合（即振型为PPPNPPP）和（2，5）组合（即振型为PPNPPNP）等模态特征。

图2 同组内7 叶螺旋桨的模态频率与振型特征Fig.2 The mode frequency and mode shape characteristics of 7-blade propeller in a modal group

1.2.2 5 叶螺旋桨模态特性

为了揭示螺旋桨模态特征的普遍性，进一步分析了5 叶螺旋桨的模态特性，如图3 所示。桨叶计算模型同图1，由在周向进行72°阵列得到。

图3 5 叶螺旋桨精细化有限元计算模型Fig.3 The refined FE calculation model of a 5-blade propeller

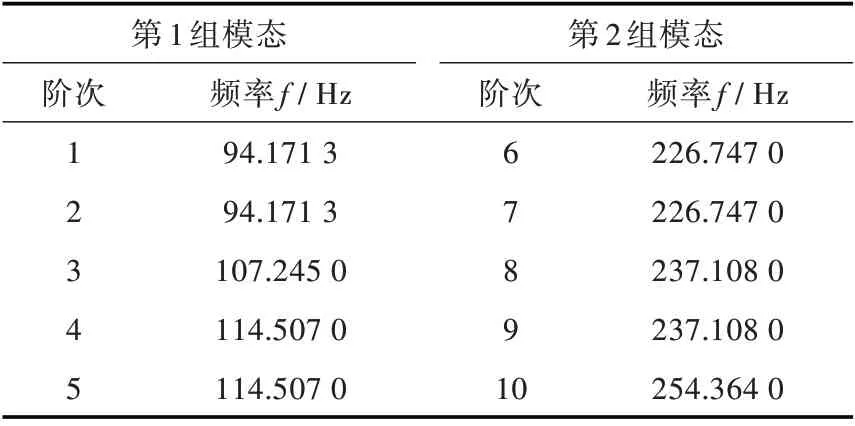
表2 给出了5 叶螺旋桨的低频模态计算结果。其低频模态同样呈现明显的分组特征，每组5 个模态。在第1 组模态中，每个桨叶的振型为其第1 阶弯曲模态振型，组内不同模态桨叶间相位关系不同；在第2组模态中，每个桨叶振型为其第2阶模态振型，组内不同模态桨叶间相位关系不同。同组内5 个模态的频率相近，不同组间的模态频率差别较大。

观察同组内模态频率和振型，发现亦呈现明显的单频和重频特征。5 个模态实际上只有3 个模态频率，其中2 个模态频率各自对应2 个模态振型，属于重频模态；1 个模态对应1 个振型，属于单频模态。

在振型特征方面（图4），单频模态振型可描述为NNNNN，即“水母模态”；2 组重频模态的振型可以描述为NPNPN（PNPNP）和NNPPP（PPNNN），两两正交。2 组重频模态的振型全部为（2，3）组合，即2 个桨叶振动与另外3 个桨叶振动反相，不存在（1，4）组合（即PPPNP）模态特征。

1.3 水介质中螺旋桨低频模态特性

为了研究介质环境对螺旋桨低频模态特征的影响，以图1 所示模型为对象，基于有限元/边界元（FEM/BEM）耦合模态分析方法［9］，建立螺旋桨数值计算模型并分析其在水环境中的模态特性。

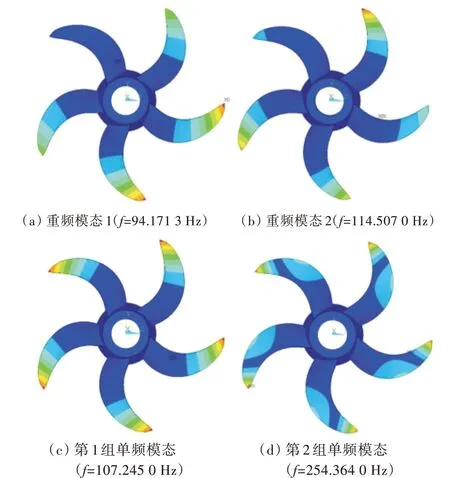
图4 5 叶螺旋桨模态振型Fig.4 The mode shapes of a 5-blade propeller

模态频率计算结果如表3 所示，模态振型特征如图5 所示。由于附连水的影响，螺旋桨的模态频率大幅降低，如“水母模态”频率由109.541 0 Hz降低到了82.051 3 Hz，但仍可观察到明显的分组特征；可观测到组内单频、重频模态的特征，亦可观测到重频模态振型仅有（3，4）组合的特点。

对比空气、水介质中螺旋桨的模态特征，以及7 叶、5 叶螺旋桨模态特征的计算结果，发现螺旋桨的低阶模态特征具有一般性规律：一是单桨叶模态的聚集分组特征；二是组内单频、重频模态特征。

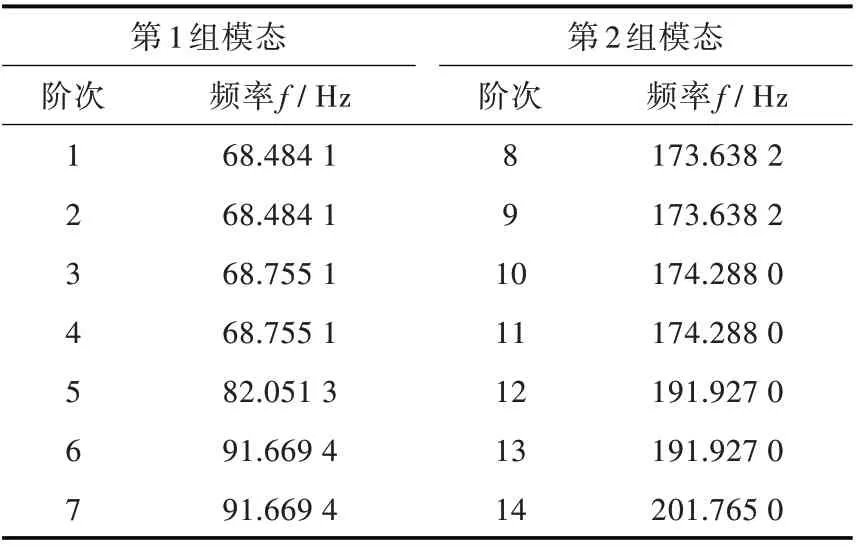
表3 7 叶螺旋桨声-固耦合弹性模态频率对比Table 3 The FEM/BEM coupling modal frequency of a 7-blade propeller

2 桨叶失谐的影响分析

上节的建模分析从几何模型、单元数量和单元阶次等方面进行了精细化的分析，确保了结构动力学意义上的理想对称性。将螺旋桨因加工误差（外形）、密度不均（质量）和微裂纹（刚度）等缺陷而无法保证完全中心对称状态的情况称为“失谐”，本节将研究螺旋桨微失谐状态下的模态特性。

在图1 所示桨模的任意叶尖设置集中质量，取值为桨叶质量1/1 000，以模拟螺旋桨的微小质量失谐。空气介质中的模态频率如表4 所示。对照表1 可见，在微失谐情况下，模态频率依然呈现分组的特征，每7 阶模态一组，第1 组模态仍以单桨叶第1 阶模态聚集；第2 组模态以单桨叶第2 阶模态聚集。此时，重频模态特征不再出现（或者不明显），7 个模态频率对应7 个振型，但“水母模态”仍然存在，模态频率有轻微的改变，模态振型基本不变（图6）。这表明微失谐对重频模态影响较大，对同相的单频模态影响较小。可据此推断，螺旋桨的“水母模态”特征比较稳定，不会因为桨叶外形、质量和刚度轻微的差别或者变化而改变。

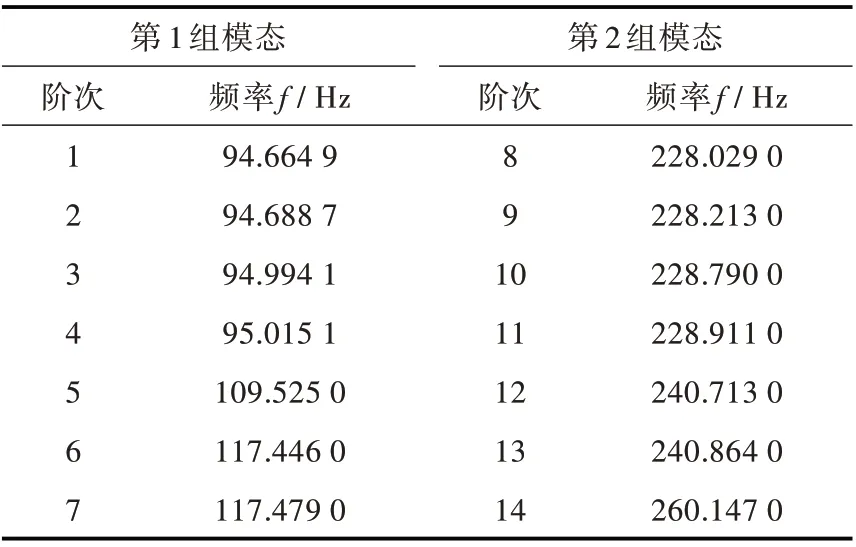
表4 7 叶螺旋桨单桨叶失谐模态频率对比Table 4 The mode frequency of a 7-blade propeller withstructural detuning

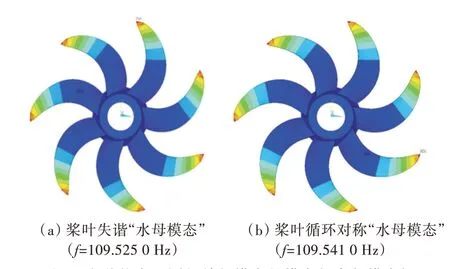
图6 失谐状态下同相单频模态的模态频率与模态振型Fig.6 The mode frequency and mode shape comparison of the single frequency mode between the propeller with structural detuning and the propeller with cyclic symmetry

3 基于循环对称结构振动理论的解读

为进一步验证基于数值计算得到的螺旋桨结构模态特征规律，揭示其内在特征，本节引用循环对称结构（指结构定轴旋转某一角度后自身及外部条件无宏观差异的结构［10］）振动理论，分析螺旋桨的模态特性。

胡海岩等［10-11］基于Cn群表示论（n 为子结构数，结构具有2πn的中心对称性）和模态综合法，提出了一般循环对称结构振动分析方法，从数学上揭示了循环对称结构的动力学特性和模态变化规律。该方法没有引入针对子结构的任何假设，具有普适性，同时根据工程分析精度的要求，还可实现降维，能大幅缩减计算量。

基于Cn群表示论，将子结构模态转化为Cn群表示空间的广义模态，进行子结构界面的调谐变换，对控制方程进行分组解耦，得到固有振动特征值问题的控制方程为

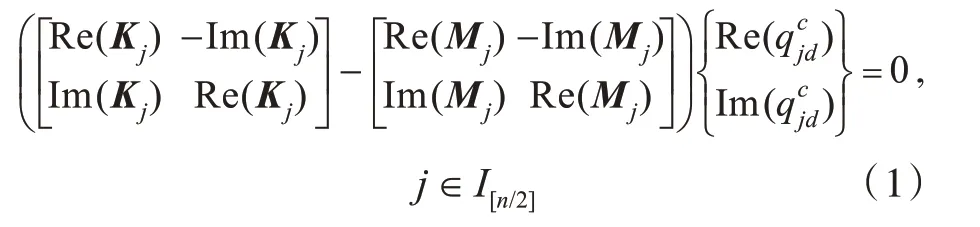
式中：Mj，Kj分别为对应结构第j组广义模态坐标的质量和刚度矩阵，其由基本子结构(0)S在(0)CS坐标系中的质量矩阵M和刚度矩阵K形成，其中(0)CS为基本子结构坐标系；Re 为取实部运算；Im 为取虚部运算；为Cn群第j 个子空间中结构广义模态坐标向量；［］表示取整。

螺旋桨是一种典型的循环对称结构，且是弱耦合循环对称结构。引用循环对称结构振动理论的主要结论进一步阐释本文对螺旋桨模态特征数值计算呈现的规律：

1）根据循环对称结构模态理论，对于弱耦合Cn循环对称结构，总体模态特征呈现出按照子结构模态阶次聚集成组的特征，每组n 阶模态，其中[(n-1)/2]个模态为重频模态。

对于7 叶螺旋桨，其数值计算体现了模态分组的特征，每组7 个模态（与子结构数相同），有3个重频模态，模态频率小数点后的4 位数完全相同。对于5 叶螺旋桨，数值计算也体现了模态分组的特征，每组5 个模态，其中2 个重频模态。

2）根据循环对称结构模态理论，Cn循环对称结构单频模态是且仅是子结构同相或者相邻子结构反相振动。这表明，当n 为奇数时，单频模态即为所有子结构的同相振动模态，也即7 叶螺旋桨的“水母模态”；当n 为偶数时，单频模态有2 种情况，第1 种为子结构的同相模态（“水母模态”），第2 种为相邻桨叶反相模态。本文7 叶和5 叶螺旋桨计算得到的单频模态均体现为同相模态。

3）Cn循环对称结构重频模态振型按以下条件满足自身周期重复性：若有正整数q(0 ＜q＜j)，使p=qn j(0 ＜j＜n2)为正整数，则Cn结构存在重频模态，以p个子结构周期重复。

分析这一结论发现，若n 为质数，就找不到满足条件的q，重频模态的振型就不具备周期性。图2、图5 的计算结果表明，7 叶螺旋桨的重频模态振型均不具备周期性特征。

4）根据循环对称结构理论，失谐对重频模态影响较大，频率和振动的特征规律会被破坏；轻微失谐对单频模态影响小，模态频率和振动变化均较小。

该分析表明，由于桨叶存在微小的质量失谐，7 叶螺旋桨的重频模态特征消失，同组内7 阶模态频率/振型各不相同，均表现为单频模态；从模态振型上看，NNNNNNN 模态依然存在，说明桨叶微小失谐会改变单频同相模态频率，但不会改变模态振型，这说明同相单频模态（即“水母模态”）是稳定的。

本节引用循环对称结构理论对螺旋桨的模态特性进行分析，并从理论上解释了螺旋桨循环对称结构的分组特征，以及组内单频模态、重频模态特性，分析了桨叶失谐对模态特性的影响。结果显示精细化有限元计算结果与循环对称结构理论分析一致，验证了数值计算解释的螺旋桨模态特征的正确性。

4 结 论

为掌握螺旋桨的低频模态特性，对螺旋桨开展了精细化有限元数值分析，并引用循环对称结构动力学理论对数值计算结果进行了验证，揭示了螺旋桨低频模态特征规律的一般性。主要得到如下结论：

1）不同介质环境、不同叶数螺旋桨低频模态计算分析表明，作为一种弱耦合循环对称结构，其低频模态具有按子结构模态聚集分组的特征；组内模态数与子结构数相同；组内模态有重频模态和单频模态；若桨叶数为奇数，单频模态为全部桨叶同相振动模态，也即工程实践中观测到的“水母模态”。

2）桨叶轻微失谐对螺旋桨重频模态影响较大，对单频同相模态影响较小，表明“水母模态”具有确定性和稳定性。

3）循环对称结构动力学理论分析结果表明，数值计算揭示的螺旋桨低频模态特征分组、单频和重频等规律具有一般性。

本文通过精细化数值仿真并引用循环对称结构动力学理论，揭示了螺旋桨低频模态特征的一般规律，为螺旋桨低频噪声机理分析与控制提供了理论和技术支撑，具有重要的工程意义。