基于新陈代谢GM(1,1)模型的我国卫生总费用预测分析*
2020-06-28高倩倩蔡伟芹马桂峰王培承郑文贵盛红旗马安宁
井 淇 高倩倩 蔡伟芹 马桂峰 王培承 郑文贵 盛红旗 马安宁△
【提 要】 目的 采用新陈代谢GM(1,1)模型对我国2018-2030年卫生总费用及其占GDP比重进行预测分析,为政府决策提供参考。方法 采用合适维度数据序列的新陈代谢GM(1,1)预测模型进行预测。结果 8维和9维数据序列新陈代谢GM(1,1)模型在预测卫生总费用及其占GDP比重方面具有更高精度。以2017年为基,经过GDP指数平减后预测我国卫生总费用实际值及其占GDP比重在2030年分别达到7.55万亿元和7.11%,在2030年其占GDP比重将达到11.09%。结论 新陈代谢GM(1,1)预测模型应用我国卫生总费用及其占GDP比重的预测具有实践意义和价值,我国卫生总费用规模和占GDP比重在2030年达到发达国家水平,建议从监测体系、控制不合理增长等方面保障卫生总费用有序发展。
“健康中国2030”已成为国家战略,如何实现《健康中国2030规划纲要》目标成为关注的焦点。作为保障卫生健康的重要资源,卫生总费用(total expenditure on health,TEH)不但可以反映地区一定时期全社会用于卫生服务的资金总额,而且可以为政策制定和政策效果监测提供依据[1-2]。灰色系统理论可利用包含不确定因素的系统进行模糊预测,随着发展应用至人口、经济、社会、管理等诸多领域[3]。其中GM(1,1)是灰色系统理论中基本模型,但是仍会存在预测精度的问题,而新陈代谢模型预测精度整体优于基本GM(1,1)模型[4-7]。基于此,本文试图通过不同维度数据,建立预测精度更高的新陈代谢GM(1,1)预测模型并进行实证研究,以期为未来相关政策制定提供方法支撑和参考。
资料和方法
1.资料来源
中国卫生总费用、中国GDP以及政府公共财政预算支出等数据均来源于2018中国卫生健康统计年鉴(中国协和医科大学出版社)、2018年中国统计年鉴。
2.新陈代谢GM(1,1)模型确立过程
(1)GM(1,1)建模步骤
第1步:设非负原始数据序列为
X(0)={x(0)(1),x(0)(2),…,x(0)(N)}
(1)
X(1)={x(1)(1),x(1)(2),…,x(1)(N)}
(2)
其中
(3)
第2步:构造累加矩阵B与常数项向量YN,即
(4)
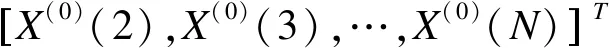
(5)
(6)
第4步:将灰参数带入时间函数
(7)

水文因素的影响是当前路基沉降中比较普遍的影响因素,目前我国的高速公路施工项目周边区域都存在地下水与江河水,路基表面也会直接受到这些水源的侵蚀或者冲击,路基底层也会因为地下水的移动而存在严重的冲击,进而导致路基出现沉降的问题,因此在进行高速建设施工的过程中,对于临近水源的工程施工项目需要多加注意,且进行准确的路基沉降监测和控制,从而可以保证公路工程的质量达到使用的需要。
(8)
对(8)式进行一次累减还原得到
(9)
(2)模型检验
为了分析模型的可靠性,必须对模型进行诊断。目前常用的通用诊断方法有两种,残差检验和后验差检验。
①残差检验
将第t时刻相对误差记为Δ(t),其公式为
(10)
(11)
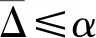
②后验差检验,检验残差分布的统计特性。
即先计算观察数据离差s1
(12)
及残差的离差s2
(13)
然后计算后验比C
(14)
最后计算小误差概率P
P={|q(0)(t)-q(0)(t)|<0.6745s1}
(15)
具体判定标准一般要求C<0.35,不超过0.65;小误差概率P越大预测模型的精度越高,P应大于等于0.7[4]。
③新陈代谢 GM(1,1)模型预测原理
首先由原始序列(1)建立灰色预测模型预测出新数据x(0)(N+1) 并将其加入到原始序列中并去除原有数据x(0)(1),接着再建立GM(1,1)模型,预测下一个数据,并补充到预测数列中,同时除去最早的一个数据,如此新陈代谢,直到完成预测目的。实际过程中并不将所有数据用来预测,要根据合适维度数据建立新陈代谢GM(1,1)模型。
结 果
由于卫生总费用统计数据自2001年起不含髙等医学教育经费,2006年起包括城乡医疗救助经费,因此本文选取中国2006-2017年卫生总费用及其占GDP比重的数据进行模型检验和预测分析。为了预测数据更加具有可比性,将2006-2017年卫生总费用和GDP的名义值均以2017年价格为基,经过GDP平减指数进行处理后的实际值进行分析(见表1),具体换算过程见文献[8]。
若利用传统GM(1,1)模型则会无法考虑未来扰动因素对卫生总费用增长的影响,影响系统的发展,导致旧数据的信息意义逐步降低[6],进而使得模型在卫生总费用预测中的精度越来越低。为更好的反映系统将来的发展趋势,首先需要采用不同维度数据对卫生总费用及其占GDP比重进行检验性预测,从而选取精度更高的GM(1,1)模型(分别见表2-3),然后方可建立新陈代谢GM(1,1)模型进行预测。为进一步保证预测模型精度,均采用的是生成数列残差模型(下同)。

表1 2006-2017年我国卫生总费用实际值及占GDP比重变动趋势表

表2 不同维度卫生总费用GM(1,1)预测模型相关参数情况表
通过表2和表3各个维度模型指标中后验比C和小误差概率P可知,各个维度模型精度等级均较好,各参数符合预测精度。在以2016年与2017年数据作为检验性预测下,两年平均预测误差也总体较小。因此,在模型基本参数均符合要求前提下,拟采用对两年数据预测相对误差平均值最小的模型。所以对我国2018-2030年卫生总费用实际值及其占GDP比重的预测分别采用8维和9维数据的新陈代谢GM(1,1)模型进行预测(如图1所示)。

表3 不同维度卫生总费用占GDP比重GM(1,1)预测模型相关参数情况表
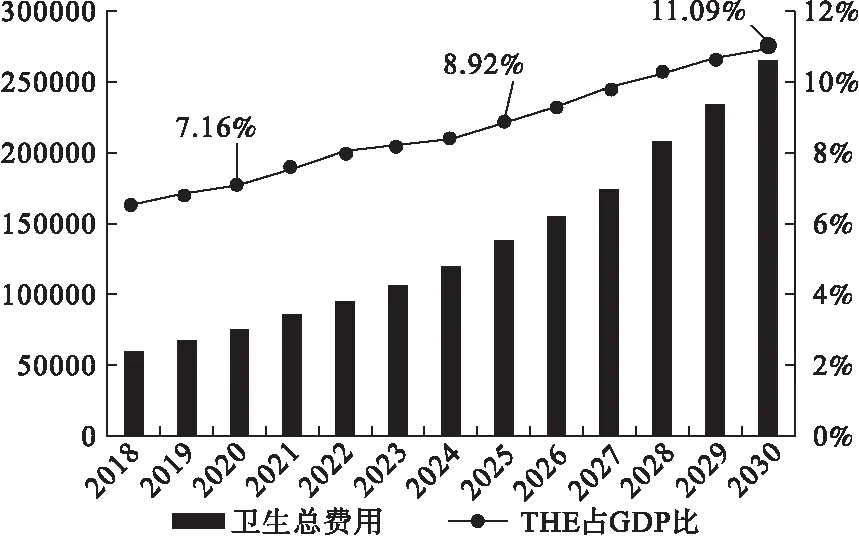
图1 新陈代谢GM(1,1)模型预测卫生总费用及其占GDP比重情况示意图
讨 论
根据预测结果,以2017年数据为基的调整后的卫生总费用及其占GDP比重在2030年之前仍然呈快速增长势头。到2020年全面建成小康社会之时,我国卫生总费用达到7.55万亿元,其占GDP比重达到7.16%,占比接近部分经济合作与发展组织(organization for economic co-operation and development,OECD)国家当前水平(2016年数据:冰岛7.6%、韩国7.7%、爱尔兰7.8%),说明全面建成小康社会目标从卫生总费用角度看指日可待。到2030年,在健康中国战略规划目标完成之时,我国卫生总费用实际值将达到2017年4倍多,近26万亿元,卫生总费用占GDP比重也将比2017年翻了接近一番,达到11.09%,与当前瑞士的12.4%接近。预测数据与OECD国家的数据对比来看,我国再经过十几年的发展,在健康中国战略引领下,到2030年卫生总费用占GDP比重将可达到发达国家水平,由此可见新陈代谢GM(1,1)模型预测结果具有科学性。但同时也要看到,卫生总费用总量的大幅度增长及其占GDP比重扩大,势必对社会经济发展带来巨大挑战,特别是当前的一段时期内,我国经济增速由高速发展转为中高速发展,社会经济发展进入新常态,也会对卫生总费用持续增长产生影响。因此,建议政府在对卫生总费用的宏观治理方面要注意以下三方面:一是有必要对卫生总费用的发展建立有效的风险监测预警机制;二是财政支出仍需进一步加大必要卫生支出保障力度,同时建立机制减少卫生总费用中不合理增长部分(如过度医疗费用、虚高药品费用等);三是贯彻新时代的卫生健康工作方针,树立以人民健康为中心,将健康融入所有政策的治理理念,用有限卫生费用增强居民生活质量。
