基于non-local先验的贝叶斯变量选择方法及其在高维数据分析中的应用*

山西医科大学公共卫生学院卫生统计教研室(030001)

马金沙 董晓强 高 倩 陶 然 许树红 李艳艳 王 彤△

【提 要】 目的 对高维数据进行变量筛选并构建预测模型是组学数据分析的研究热点之一。本研究旨在为结局为二分类变量的高维组学数据筛选自变量并构建预测结局的稀疏统计模型。方法 本研究通过模拟研究和实例分析阐释基于non-local先验的贝叶斯变量选择方法——乘积逆矩先验(product inverse moment，piMOM)相较于惩罚类方法ISIS-光滑平切绝对偏差(iterative sure independence screening-smoothly clipped absolute deviation,ISIS-SCAD)和ISIS-最小最大凹惩罚(iterative sure independence screening-minimax concave penalty,ISIS-MCP)在高维数据中变量筛选及其预测效果的性能优劣。结果 模拟研究发现：在高维的情况下，经piMOM、ISIS-SCAD和ISIS-MCP方法筛选所得变量的平均真阳性数和受试者工作特征曲线下面积(AUC，area under curve)基本相等，ISIS-SCAD、ISIS-MCP的平均假阳性数、回归系数均方误差以及预测均方误差明显高于基于non-local先验的贝叶斯变量方法所获得的对应值。piMOM方法分析弥漫大B细胞淋巴瘤实例数据共识别5个有意义的基因，AUC为0.996；ISIS-SCAD识别7个基因，AUC为0.975；ISIS-MCP识别7个基因，AUC为0.968。结论 在模型选择相合性和预测准确性方面，piMOM方法与ISIS-SCAD和ISIS-MCP相比，具有优势，在一定意义上可有效控制假阳性率。

测序技术的发展催生大量组学数据，此类数据中，变量个数p远大于观测个体数n(p=O(n))且变量间往往呈现高度相关性，称为高维数据[1]。目前，解决高维数据变量筛选问题有三种基本思路：最优子集选择、惩罚以及贝叶斯方法。最优子集选择方法在低维数据中表现良好，但在高维数据中，估计结果不稳定，加之其较大的计算量，不再适用。

惩罚类方法以惩罚项为依据，分为光滑平切绝对偏差[2](smoothly clipped absolute deviation,SCAD)、自适应Lasso[3](adaptive lasso,aLasso)、最小最大凹惩罚[4](minimax concave penalty,MCP)等多种类型。在高维数据中，因计算量较大使惩罚类方法的运用受到限制。基于该问题，Fan和Lv[1]于2008年提出具有sure screening 性质的(I)SIS(sure independence screening)方法，并通过模拟研究阐明了其应用于高维数据分析时的良好效果。2016年，王彤团队[5]将ISIS+Lasso、ISIS+SCAD、ISIS+MCP三种方法分别应用到模拟研究和实例分析中，探讨了其应用于高维数据二分类结局资料中实现变量选择目的时的表现。

贝叶斯方法使用马尔可夫链蒙特卡洛算法(Markov chain Monte Carlo algorithm,MCMC)，从后验分布中抽取待估计的参数值。2010年，基于贝叶斯假设检验理论，Johnson和Rossell等人[6]将贝叶斯先验分为两类：local 与non-local 先验。2010年，Johnson和Rossel等[6]引入乘积逆矩(product inverse moment,piMOM)和乘积矩(product moment,pMOM)。2013年Rossell等[7]提出乘积指数矩(product exponential moment,peMOM)，同时探究各贝叶斯方法用于高维数据变量选择的性能。上述三种先验均为non-local先验，见图1。该图提示在高维组学数据变量选择方面，基于non-local先验的贝叶斯方法优于local先验。

本文首先阐释基于non-local先验的贝叶斯变量筛选方法——piMOM，继而通过模拟研究和实例分析探究其在高维数据中的应用，从而比较piMOM、ISIS-SCAD、ISIS-MCP方法在高维数据中进行变量筛选的性能优劣。

图1 备择假设下模型参数先验分布的比较左：local先验 右：non-local先验

原理与方法

1.基于ISIS的惩罚类方法

该方法实现分为两个阶段：第一阶段，从高维数据的多个自变量中识别出与结局变量相关性相对较强的变量。第二阶段，基于惩罚类思想，从与结局变量强相关的变量中筛选出真正具有意义的自变量，本研究选用SCAD、MCP两种惩罚类方法。其中SCAD[2]的惩罚项为：

(1)

MCP[4]的惩罚项为：

(2)

α，λ为调整参数。

2.基于non-local先验贝叶斯变量选择方法：piMOM

应用该方法进行变量筛选时，需对模型参数先验分布、包括模型空间先验进行合理设定，并使用恰当方法以先验和似然获得的模型为依据估计后验概率，这两个过程是保证贝叶斯方法能够合理进行变量选择的关键。

(1)模型参数先验分布及其超参数设置

本文采用的non-local先验为乘积逆矩先验，表达式为：

(3)

其中，τ,γ>0为piMOM的两个超参数。τ为尺度参数，γ为形状参数。上述两个超参数分别决定先验函数0附近和两端尾部的分布情况。某种意义上，所构建模型中参数的最小值由尺度参数τ决定。针对“如何对τ值进行合理选择”这一问题，Nikooienejad[8]于2016年给出相关建议：数据经标准化后，能使原假设下和备择假设下概率密度函数交叉面积低于一定阈值(p-α)的最大τ值，即为合理τ值。合理选取该值能在有效控制模型的假阳性率(两者密度函数交叉部分)的同时，保证模型具有较高的灵敏度，见图2。

图2 基于non-local先验贝叶斯变量选择方法中超参数选择的模拟图

(2)模型空间先验

模型k的beta-binomial先验[9]表达式为：

(4)

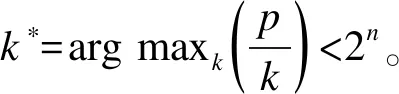
(2)模型的后验概率

基于贝叶斯理论知识，后验概率公式可记为：

(5)

通过(5)式可获得最高后验概率模型(highest posterior probability model,HPPM)。鉴于参数空间的高维属性和后验概率密度函数的复杂属性，本研究运用MCMC算法实现HPPM模型的最大化。同时，对各边际概率密度函数进行普拉斯(Laplace)近似处理以达到降维目的。其中，对应于模型k的边际概率密度函数如下所示：

(6)

(7)

最大后验估计值可借助函数nlminb()完成计算。通过上述所示赫氏矩阵表达式可求得目标函数f(yn,βk)的局部极小值，在此基础上利用该局部极小值得到边际概率密度函数最大值(mk(yn))，最终获得后验概率。Johnson等人[10-11]于1998年改进收敛性评价方法，提出校正成对诊断(modified coupling diagnostic)，本文即选用该方法对马尔可夫链蒙特卡洛算法的收敛性进行评价。

3.软件实现

本文运用R 3.3.2软件进行统计分析。采用Fan[12]2015年提供的SIS包实现两类惩罚类方法ISIS-SCAD和ISIS-MCP，并采用十折交叉验证方法进行调整参数选择[13]，根据Fan等的建议[2]，对SCAD方法，令a=3.7，对MCP方法，令a=3。采用2012年Johnson等人[14]提供的mombf包以实现基于non-local先验(piMOM)的贝叶斯变量筛选方法。同时调用snowfall并行运算包以达到提高贝叶斯方法运算效率的目的。

模拟试验

1.模拟研究设计

本研究样本量设置5个水平，分别为50，100，200，400和600。自变量个数设置两个水平，分别为1000和3000，该设置满足Li和Fan提出的高维数据条件[1]。以Minsuk Shin[15](2015)模拟情境设置作为参考，假定模型k包含5个有效(即真正具有意义)自变量，并设自变量x服从均值0，协方差为∑的多元正态分布，即xi～Np(0,∑)，其中∑可分为如下不同情况：

方案一：令各自变量间互不相关，即∑jj′=0，j≠j′且∑jj=1，1≤j，j′≤p。

方案二：令各自变量间呈复合对称相关，即∑jj′=0.5，j≠j′且∑jj=1，1≤j，j′≤p。

方案三：令各自变量间呈自回归相关，即∑jj′=0.5|j-j′|，j≠j′且∑jj=1，1≤j，j′≤p。

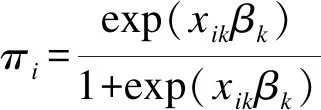
2.模型评价指标

所构建模型优劣的评价从两个方面进行：模型选择相合性和模型预测准确性。

(1)模型选择相合性

模型选择相合性的定义为三种方法所构建模型与真实模型相一致的程度。可使用假阳性数(false positive,FP)和真阳性数(true positive,TP)进行评价。本研究中平均真阳性数越接近模拟情境中设置的真正有意义的变量数5，平均假阳性数越接近0，则模型选择相合度越高。

(2)模型预测准确性

模型预测准确性定义为三种方法所构建模型预测的结局与真实结局的一致程度。可使用回归系数均方误差(mean squared error of regression coefficient,RMSE)、预测均方误差(mean squared error of prediction,PMSE)、以及受试者工作特征曲线下面积(area under curve，AUC)进行评价。PMSE和RMSE越小，则所构建模型越接近真实模型，预测越准确。AUC值越大，提示模型分辨能力越高，预测越准确。

3.模拟结果

(1)超参数选择的模拟结果

piMOM方法在方案一中的超参数选择结果如表1，方案二和方案三超参数选择结果表2，表3。

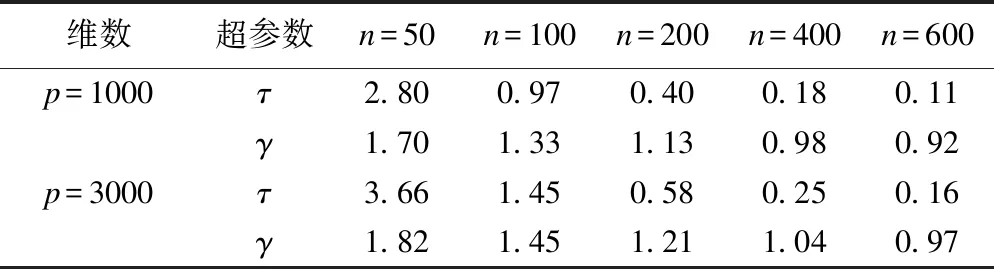
表1 方案一piMOM方法的超参数选择

表2 方案二piMOM方法的超参数选择

表3 方案三piMOM方法的超参数选择

由以上超参数选择结果可知：超参数τ和γ随着数据维数的增高而增大；反之，即数据维数降低时，超参数τ和γ随之逐渐减小。

(2)自变量选择的模拟结果

方案一模拟结果见图3(方案二和方案三见图4，5)。

对于piMOM方法，协方差矩阵结构和样本量一定时，模型TP、FP、PMSE、RMSE、AUC以及所获得模型总变量数随自变量维数变化较小。协方差结构和自变量维数一定时，样本量增加，TP增加明显；FP始终处于较低水平，相对稳定；PMSE在样本量达200之前下降较快，其后相对稳定；RMSE相对稳定，始终处于较低水平；AUC相对稳定，均>0.8；所获模型总变量数随样本量增加逐渐增加，直至获得所有的真阳性变量。自变量维数和样本量一定时，协方差结构改变，预测模型性能指标变化较小。

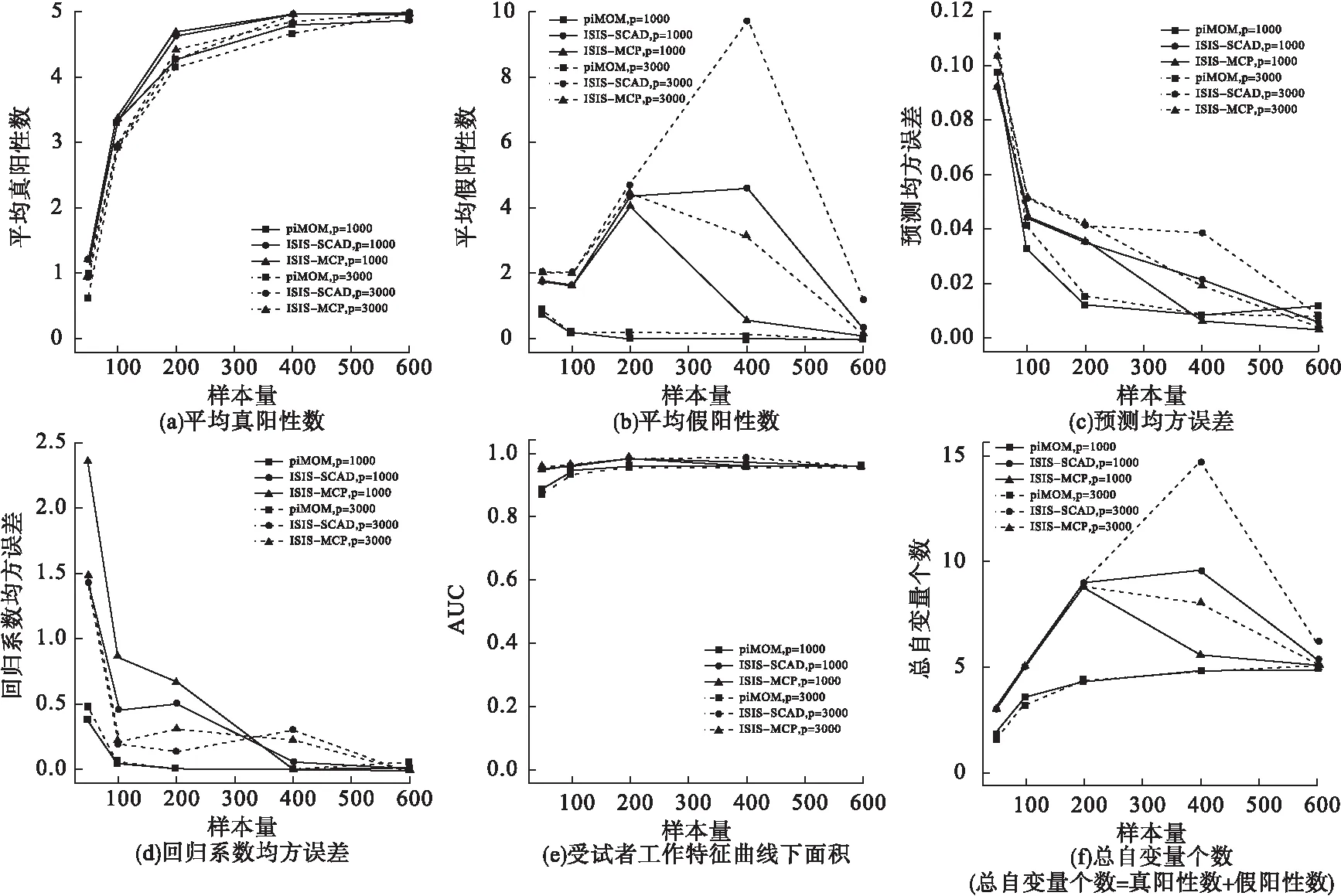
图3 方案一的模拟结果

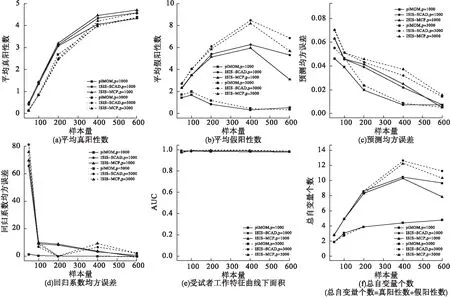
图4 方案二的模拟结果

图5 方案三的模拟结果

对惩罚类方法ISIS-SCAD和ISIS-MCP，协方差矩阵结构和样本量一定时，模型TP、PMSE、RMSE、AUC以及所获得模型总变量数随自变量维数变化较小。协方差结构和自变量维数一定时，样本量增加，TP明显增加；FP呈现先上升后下降的趋势，且均在筛得所有真阳性变量前取得最大值；PMSE和RMSE在样本量达100之前下降较快，其后相对稳定；AUC变化不大，始终>0.8；所获得模型总变量数逐渐增加，直至获得所有的真阳性变量。自变量维数和样本量一定时，协方差结构改变，预测模型效性能指标变化较小。

给定某一特定高维情况，在模型选择相合性方面，piMOM方法所获得模型的TP与ISIS-SCAD、ISIS-MCP大致相等，FP小于两类惩罚类方法。在模型选择准确性方面，piMOM方法所获得模型的PMSE、RMSE以及AUC小于两类惩罚类方法。在模型选择稳定性方面，piMOM方法各评价指标相较于两类惩罚类方法变化幅度较小。

实例分析

1.数据来源

本研究所使用数据集可在高通量基因表达数据库(gene expression omnibus,GEO)中获得，GEO数据库链接为https：//www.ncbi.nlm.nih.gov/geo/，数据集相应编号为GSE10846。该数据集包含性别、治疗方案、国际预后指数(international prognostic index,IPI)、中位生存期以及基因表达信息，共420个样本，54675个基因。因现有认知中，DLBCL共分为3型：生发中心B细胞样型(germinal center B cell-like,GCB)，预后较好；表达活化的外周血B细胞和浆细胞特征基因的活化外周血B细胞样型(activated B cell-like,ABC)，预后较差；无明确特征的异源性类型，即第3型，预后较差[16-17]。因第3型不明确，为排除性定义，且该型样本量仅为总样本量的1/6(70/420)，故本研究考虑将第3型排除，选择DLBCL的两个分子学亚型：ABC(167)和GCB(183)进行探究。

2.研究方法

首先使用R软件包Bioconductor中的limma包对原始数据进行经验贝叶斯差异表达分析[18-19]，继而借助四分位数间距[20]对数据进行降维处理，从而获得包括350个样本(ABC：167；GCB：183)，3237个基因进行最终变量选择的样本集。本研究采用十折交叉验证方法识别有效基因，以保证结果稳定性。经10次筛选后，将频数大于5的变量作为有效基因选入最终模型。

3.结果

piMOM方法筛选结果显示：共有5个有意义的基因(TNFRSF13B，BATF，LMO2，SYTL4，PALD1)，AUC为0.996；ISIS-SCAD结果显示：共有7个有意义的基因(MYBL1，CYB5R2，MAML3，S1PR2，ASB13，ZBTB46，BATF)，AUC为0.975；ISIS-MCP结果显示：共有7个有意义的基因(CYB5R2，MAML3，S1PR2，ASB13，ACVR2A，TNFRSF13B，BATF)，AUC为0.968。详见表4

表4 三种方法基因选择结果比较

*：“_”为已有文献报道与DLBCL分型有关的基因。

讨 论

本文将piMOM方法应用到高维数据中构建二分类logistic回归模型并实现变量筛选，继而以模拟研究和实例分析两种途径探讨其相对于两种惩罚类方法ISIS-SCAD、ISIS-MCP的优劣。

模拟研究表明：相比于ISIS-SCAD和ISIS-MCP，piMOM方法在模型选择相合性方面能准确筛选有效自变量，具有较小的假阳性率；模型预测准确性方面其PMSE和RMSE均较小。这种结果是由贝叶斯方法和传统惩罚类方法在较小非0模型参数附近不同的概率密度函数所导致：从贝叶斯角度看，两类惩罚类方法SCAD、MCP方法倾向于使得较小非0模型参数附近先验概率更大，相当于在模型参数上施加local先验；而piMOM方法则不同，其通过BIC模型赋予较小非0的模型参数以较小的先验概率，原理如下：BIC模型选择的目标函数为：

(8)

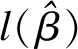
(9)

d>0，通过对(8)、(9)式的比较可知：以BIC为基础，增加一个惩罚项后即可获得piMOM目标函数，这使得piMOM方法给予0附近(包含0)模型参数以无穷大惩罚，从而保证所建立终模型的假阳性率较小。

在模拟研究中，经ISIS-SCAD和ISIS-MCP方法筛选所获得模型，变量的假阳性数呈现先上升后下降的趋势，推测原因如下：在自变量个数p不变的情况下，随着样本量的增加，数据提供的信息会越多，所能筛得的总的自变量个数相对增加，起初真阳性数和假阳性数都随之增加，至获得所有真阳性自变量前，模型中所获得的真阳性变量渐能代表样本信息，假阳性数继而出现下降趋势，直至获得所有真阳性数时，假阳性数降至最低。而对于贝叶斯而言，则可以通过先验分布中超参数值的选择控制假阳性数始终处于较低水平。

实例研究表明：基于non-local先验的贝叶斯变量筛选方法所构建的模型能够以较少的变量数，获得与ISIS-SCAD、ISIS-MCP近乎相同的AUC。若将贝叶斯变量筛选的结果应用于实践，可缩小后期进行实验验证的探索范围，降低经济成本，为更好地进行疾病机制研究提供便利。从这一角度上讲，基于non-local先验的贝叶斯方法相较于惩罚类方法更可取。

本探究尚有不足之处：(1)贝叶斯变量筛选方法运算量较大，将其应用于高维组学数据时，该问题带来的计算困难尤为突出，如何提高贝叶斯方法的计算效率，为该领域亟待解决的问题；(2)本文未将基于local先验的贝叶斯变量选择方法与non-local先验同时应用到二分类结局变量资料的高维数据中，以完成两种先验之间的对比，关于贝叶斯方法变量选择性能尚需作进一步探究。