零膨胀计数资料几种模型方法的比较研究*

复旦大学公共卫生学院流行病学教研室(200032) 吴学福 刘振球 吴明山 方绮雯 袁黄波 张铁军

【提 要】 目的 探讨处理零膨胀计数资料的几种模型之间的比较及其应用。方法 在R语言中，分别用Poisson回归、负二项回归、零膨胀模型和hurdle模型来拟合66岁以上老年人医疗保健需求的数据，并通过似然比检验、Vuong检验和AIC、BIC的比较，对模型进行评估。结果 零膨胀负二项模型和负二项hurdle回归模型对数据的拟合效果优于其他回归模型，负二项hurdle模型的拟合结果与数据更接近，其拟合结果显示老年人住院天数越长、患有慢性病数量越多、受教育年数越久、参加私人保险，其访问医疗诊所的次数越多，而自评健康状况良好、男性的老年人医疗诊所访问的次数较少，即医疗保健需求的次数较少。结论 零膨胀负二项回归模型和负二项hurdle模型处理零过多、过离散数据的效果优于一般的计数模型；而在零观测值相对较少的情况下，用负二项hurdle模型可能更合适。

医学研究中经常会遇到某事件发生次数的资料中含有大量的零，即许多观察个体在单位时间、单位体积内未观察到相应事件的发生[1]。这些资料零观测值出现的概率远远超出相同条件下标准计数模型(如Poisson回归和负二项回归模型)能够预期的范围，使模型的方差远大于期望，这种现象称为零膨胀(zero-inflated)现象。零膨胀现象一直受到国内外学者的广泛关注和研究，当计数资料中存在零膨胀现象时，如果继续使用Poisson回归或负二项回归模型来拟合数据，所得结果可能失真。近年来，hurdle回归模型和零膨胀回归模型不断发展，在医学、金融、农业和社会科学等研究领域中得到广泛应用，逐渐成为分析零膨胀数据的主流模型。

原理和方法

1.零膨胀回归模型(zero-inflated model，ZIM)

零膨胀模型认为计数数据中的零观测值来源于两部分：一部分是来源于数据中存在某些特殊结构而产生的结构零；另一部分是来源于Poisson分布或负二项分布产生的抽样零[2-3]。零膨胀模型可以看作是Bernoulli分布和离散型分布组成的混合分布，其概率密度函数的一般形式为：

(1)

其中πi(0≤πi<1)为零膨胀参数,表示结构零的概率，f(yi)服从某个离散型分布，如Poisson分布或负二项分布等。

(1)零膨胀泊松回归模型(zero-inflated Poisson model，ZIP)

若(1)式中的f(yi)服从参数为μ的Poisson分布时， ZIP的公式为：

(2)

其中γ,β为待估计的模型回归系数；x,z为协变量，二者可以相同也可以不同。

(2)零膨胀负二项回归模型(zero-inflated negative binomial model，ZINB)

若(1)式中的f(yi)服从参数为μ和α的负二项分布时，ZINB的公式为：

(3)

其中γ,β为待估计的模型回归系数；x,z为协变量，二者可以相同也可以不同。零膨胀模型中πi常用的连接函数为logit、probit函数。

2.hurdle回归模型

hurdle模型认为数据中的零观测值均来自于结构零，非零数据则是来自于不同的过程：第一个过程决定零事件发生还是非零事件发生的可能，发生取1，不发生取0，这个过程服从(0，1)分布，当第一个过程取0时则进入第二个过程，即事件至少发生一次的过程，该过程的非零数据服从零截断Poisson或零截断负二项分布等零截断离散分布模型[4]。

根据以上原理hurdle模型的一般形式为：

i=1,2,…,N

(4)

式(4)中πi为事件数取0的概率;f′(Zi)表示零截断离散型分布。

(1)Poisson-hurdle回归模型(Poisson hurdle model，PH)

当(4)式中的f′(Zi)选择零截断Poisson分布时[5]，PH的公式为：

i=1,2,…,N

(5)

(2)负二项hurdle回归模型(negative binomial hurdle，NBH)

当(2)式中的f′(Zi)选择零截断负二项分布时[6]，NBH的公式为：

i=1,2,…,N

(6)

hurdle模型中πi选择不同连接函数(logit、probit、clog函数等)可得到不同的二分类回归模型。

3.模型的评价指标

(1)似然比检验(LRT) 似然比检验是用来比较两个嵌套关系模型(模型1嵌套于模型2)的拟合优度。在R语言中，可以通过lrtest()函数来实现。似然比检验统计量为：

LR=-2[LL2-LL1]

(7)

(8)

(3)AIC和BIC准则 当似然比检验和Vuong检验难以判断模型优劣时，可以通过比较AIC和BIC统计量的相对大小来对模型优劣进行排名，信息准则值越小则模型越优[9]。

实例分析

本研究数据来源于1987-1988年美国国家医疗费用调查(national medical expenditure survey，NMES)关于老年人(66岁以上)医疗费用支出的调查资料。该研究共纳入了4406名医保覆盖的老年人，本文对其住院天数、健康状况自评、慢性病数量、性别、受教育年数和是否参加私人健康保险进行分析，以医疗诊所访问次数作为老年人医疗保健需求的测量指标，探讨老年人医疗保健需求的影响因素。

医疗诊所访问次数的取值分布如图1所示。

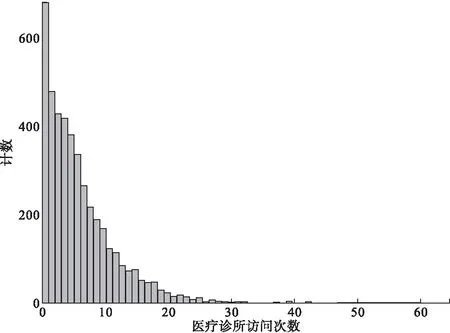
图1 医疗诊所访问次数的取值分布

图1中，医疗诊所访问次数取值为0的比例为15.5%，运用R中的dispersiontest()函数对访问次数资料进行过离散检验，检验统计量为11.509(P<0.05)，提示数据存在零过多和过离散的现象，使用零膨胀或hurdle回归模型处理数据优于Poisson回归模型。

对零膨胀和hurdle回归模型的两个部分(零部分和非零部分)均选取住院天数、健康状况自评、慢性病数量、性别、受教育年数和是否参加私人健康保险作为其协变量。分别用Poisson、负二项回归(negative binomial，NB)、ZIP、ZINB、PH和NBH模型对老年人医疗健康需求数据进行拟合，并对嵌套关系模型进行似然比检验、非嵌套模型进行Vuong检验，检验结果如表1所示。

表1 各模型的似然比检验和Vuong检验结果

*：P<0.05；**：P<0.001

似然比检验和Vuong检验结果显示，NB的拟合效果优于Poisson回归；ZIP的拟合效果优于Poisson，但比NB差，以此类推。NBH虽然优于其他模型，但与ZINB比较的检验统计量V值小于1.96，不能区分二者的优劣程度。各回归模型的参数估计结果及拟合指标AIC、BIC如表2所示。

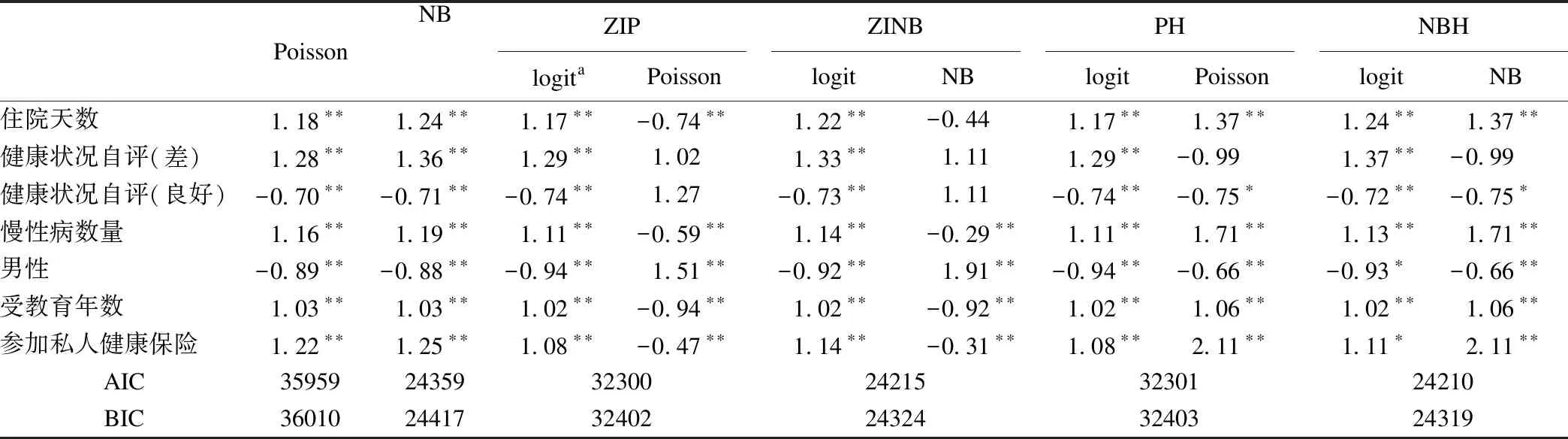
表2 老年人医疗保健需求回归模型参数估计结果

a：零膨胀的logit部分(零过程)；*：P<0.05；**：P<0.001

表2中AIC、BIC的结果验证了表2中ZINB和NBH优于Poisson、负二项回归模型、ZIP和PH，并补充说明了NBH对本研究数据的拟合效果最好。

讨 论

对于具有零膨胀现象的数据，使用Poisson和负二项回归得到的结论可能过于乐观。本研究数据在使用标准计数模型时发现住院天数、健康状况自评、患慢性病的数量、性别、受教育年数、是否参加私人保险均与老年人访问医疗诊所次数的多少有关，而NBH模型却发现自评健康状况差和医疗诊所的次数并无明显联系，实际上，医疗诊所的访问次数是需要根据医生的建议来决定的。因此，NBH模型更加贴合实际情况。

零膨胀回归模型和hurdle回归模型均是处理零过多、过离散数据常用的两个模型，但二者的主要区别在于对数据中零观测值的处理：零膨胀回归模型假设零数据来自两个不同的总体(或两种不同的分布)，一部分是那些不可能发生某事件的个体，源于数据的特殊性，假定服从二项分布；另一部分就是那些有可能发生某事件的个体，但由于抽样的存在而没有观察到事件的发生，这部分一般假定服从离散型分布。hurdle回归模型是假设数据中的零部分和非零部分是完全分开的，零数据均服从二项分布，其余的非零计数数据则是服从零截断的Poisson分布或负二项分布。零膨胀模型和hurdle模型在公共卫生、临床和社会经济等调查研究中都受到广泛重视。有学者在对交通事故伤亡的影响因素研究中发现，零数据的比例为59.07%时，用PH回归模型比NBH模型优[7]。而本研究中NBH回归模型对数据的拟合效果更好的原因可能在于：数据中零观测值相对较少，为15.5%，这对零观测值只有一个来源并与非零计数截然分开的hurdle回归模型更合适。

本文只讨论了零膨胀和Hurdle模型在老年人医疗保健次数影响因素研究中的应用并进行比较，实际的调查研究中还存在许多零膨胀计数资料。在应用回归模型进行数据拟合时，不仅要考虑数据的性质和分布，还要综合考虑实际情况和专业性，从而选择最优模型。