贝叶斯方法在篮子试验设计中的应用*

南京医科大学公共卫生学院生物统计学系(211166)

谭明敏 杨 旻 仲子航 于全骥 于朝雷 周佳薇 倪森淼 蔡丽馨 于 浩△ 柏建岭△ 陈 峰

【提 要】 目的 探讨贝叶斯方法和Simon二阶段方法应用于篮子试验设计的优劣及实例分析判断试验疗效。方法 模拟研究针对二分类结局变量，考虑不同试验层数、期中分析纳入人数等参数设置，比较两种方法的篮子试验设计在检验效能、控制I错误率及样本量的区别，并通过实例来介绍其应用。结果 模拟试验结果表明，除异质性较高的2种情景外，贝叶斯方法的篮子试验设计效能均高于应用Simon二阶段方法，且对假阳性率控制更为严格，代价便是无效篮子增多时检验效能降低。贝叶斯方法的篮子试验的样本量总体较少，尤其在试验层数较多和同质情况下。结论 贝叶斯方法的篮子试验更加灵活，可借用层间信息，相比Simon二阶段方法，更严格地控制整体一类错误率，且在试验层数和期中分析次数多时更节省平均总样本量。

2014 年，美国肿瘤研究学会(American Association for Cancer Research，AACR)在肿瘤研究进展里提出了针对精准肿瘤医学的创新性临床试验——篮子试验[1]，同年美国临床肿瘤学会的会议也多次提到了篮子试验[2]。篮子试验是一种新型临床试验模式。FDA 发布的主方案中提到，篮子试验指旨在评估单药或药物联合在不同群体(通过疾病分期、组织学、治疗史、基因、标志物或人口统计学特征来定义)中疗效的试验设计。篮子试验具体设计框架如图1，对几种不同(但相关)的疾病使用相同治疗，和针对单一肿瘤组织学患者使用单一治疗方式的传统临床试验相比更具有治疗潜力，并减少了成本和研究时间[3]。

根据药物作用机制和患者分子变异选择，可将篮子试验划分为以下三种类型[4]：(1)研究单药在靶点为相同分子变异的多种肿瘤类型中的疗效，例如Hyman[5]等人研究BRAF口服抑制剂维罗非尼治疗含有BRAF V600E突变阳性的不同组织学非黑色素瘤患者的疗效。这项研究表明，与组织学无关的生物标记物选择的篮子设计是可行的。(2)研究单药在靶点为少数分子变异的多种肿瘤类型中的疗效，例如试验AcSe′[6]和CREATE，均是评估克唑替尼治疗含有ALK和/或MET等变异的多个肿瘤患者队列疗效的大型篮子试验。(3)研究多个靶向药在多种分子变异的多种肿瘤类型中的疗效，例如试验NCI-MATCH[7]、基因泰克的MyPathway[8]，诺华的Signature[9]及美国临床肿瘤学的TAPUR[10]，这些研究定义的药物突变特异篮子目的是确定某些具体通路的靶向药的有效性。篮子试验没有固定模式，因此，它的多样性及普适性的特点非常适合在靶向治疗时代推广应用。

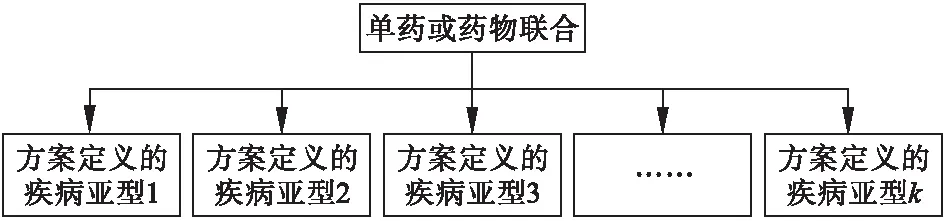
图1 篮子试验示意图

Simon[11]等人在肿瘤精准医学背景下开发了一种应用贝叶斯方法评估单药治疗不同原发部位缓解率的篮子试验。该设计已经开发了网上的应用平台以及相应软件，在网页“https：//brbnci.shinyapps.io/BasketTrials/”可以进行查看使用。本文将具体介绍这种基于贝叶斯方法的篮子试验，并与基于Simon二阶段设计方法的篮子试验进行模拟试验，比较不同疗效情景下的样本量和错误率以及不同试验层数设置下的总样本量和整体一类错误率，并通过案例介绍贝叶斯方法的实际应用。

设计概述

1.基于贝叶斯方法的篮子试验

假设按k个原发部位或组织学类型进行分层，我们用pk来表示每一层未知的反应率，假设pk有两个取值，表示药物有研发前景的高反应率phi或无研发前景的低反应率plo。H0假设每层反应率都是相等的，换言之就是药物活性不取决于肿瘤原发部位/组织学类型，所有层均有效或是均无效。原假设若为真，则设定各层反应率相同且取值为phi的概率为γ。H1假设每层反应率是互相独立的。对于每层，γ=Pr[pk=phi|H1]，此外，λ为各层完全相关的先验概率，即λ=P(H0)。

在任何期中分析中，我们都可以计算每层反应率的后验概率，与事先预设的界值T和1-T作比较，具体的计算流程见图2(A)，设计流程见图2(B)。

图2 期中分析时评估各层药物疗效的计算流程及决策的设计流程

我们定义b(r；p，n)是二项分布的概率密度函数，表示当反应率为p时，n例受试者中恰好有r例受试者缓解的概率。在期中分析时，假设在k层治疗的nk例患者中有rk人缓解，H0的后验概率为：

药物对第k层有疗效的后验概率的计算公式如下：

Pr[pk=phi|data]=Pr[pk=phi|data& H0]Pr[H0|data]+Pr[pk=phi|data& H1]Pr[H1|data]

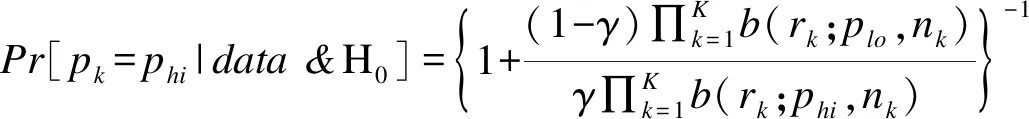
当同质的后验概率非常小时，表示层间几乎没有信息共享。如果后验概率小于1-T因无效提前终止该层试验，若后验概率大于T则因高效提前终止，这种自适应设计节约资源，并可惠及患病率低的患者群体，此外早期阳性结果可以促进该层随后的扩展队列II期试验研究。

该贝叶斯篮子设计涉及到了四个参数，分别是药物有效的反应率phi、药物无效的反应率plo、H0的先验概率λ和在任意层有效的概率γ。对于已获批用于某些原发部位药物，在篮子试验里我们通常建议λ和γ的取值分别为0.33和0.5[11-12]。随着患者群体的增加，传统II期试验设计就不再合适，在这个组学技术和个性化医疗的时代，上述的这种贝叶斯篮子设计易于修改适应各种情形。为了推广贝叶斯篮子设计，Simon提出两个方法，其一就是让λ和/或γ服从一个独立先验，其二就是构建一个“pmodal”去试图削弱完全同质或完全独立的假设[12]。

模拟试验

1.参数设置

篮子试验中的子研究通常包括主要终点指标是总缓解率的单臂试验。1989年，Simon提出了最优化二阶段设计和最小最大值二阶段设计，这两种设计在之后的单臂二阶段临床试验中应用非常广泛，也会出现在篮子试验中，即每个子研究单独应用传统Simon二阶段设计[13]。

本文通过模拟试验去比较层数为5时应用Simon二阶段设计方法和贝叶斯方法的篮子试验的操作特征。首先设置药物有效反应率phi=0.25和无效反应率plo=0.05，指定先验概率λ=0.33和任意层有效的概率γ=0.5，界值T参考BATTLE I临床试验[14]，建议后验概率若超过0.8则认为有临床活性。此外假设各层的患病率相等，且当疗效的后验概率小于0.2或大于0.8时停止纳入病人，如果期中分析试验层没有全关闭，则达到提前设置的最大总样本量时结束试验。在Ⅰ类错误和Ⅱ类错误均为0.2的条件下，使用Simon优化二阶段设计计算出第一阶段需要纳入6人，若至少有1人有疗效则第二阶段继续纳入10人，同样条件下，使用Simon最小最大二阶段设计计算出第一阶段需要纳入10人，两阶段共需纳入11人。当对试验药物信心不足时，希望确实无效时尽早终止试验，我们偏向选择最优化设计，而对试验药物有信心时，可以选择最小最大设计。因为传统篮子试验大多是II期探索性试验，所以我们更偏向选择最优化设计。为了与每层单独应用Simon二阶段设计的传统篮子试验可比，我们设置N为应用Simon优化二阶段设计的最大样本量，即80(试验层数为5时)，每次期中分析纳入5个人。模拟试验的结果见表1、表2和图3，每种情形结果均是基于1000次模拟试验得到的。

2.模拟结果

试验层数为5的篮子试验中会出现6种情形(从全部有效到全部无效)，在每一种特定情形下我们去比较应用Simon二阶段设计方法和贝叶斯方法的篮子试验在无效假设下的拒绝率和实际样本量，结果见表1。所有情形下，Simon二阶段两种设计的样本量相差不大，前4种情形优化设计比最小最大设计所需样本量要大，随着无效篮子增多，差异越来越小，无效篮子占大多数时，最小最大设计的样本量将反超。贝叶斯方法因为期中分析能自适应关闭试验层，相比传统篮子样本量有明显优势。此外，应用贝叶斯方法的篮子设计在同质情况(情形1和6)下样本量最少。从表中我们可以发现，应用优化Simon二阶段的传统篮子设计的Ⅰ类错误率均能控制在12%左右，相比应用最小最大Simon二阶段的传统篮子设计的Ⅰ类错误率稍高，情形2和3中，应用贝叶斯方法的篮子设计的无效层的Ⅰ类错误率稍高于Simon二阶段的篮子设计，但随着无效篮子增多，贝叶斯篮子设计对Ⅰ类错误率的控制逐渐显示出优势，尤其在情形6所有层均无效时对每层的Ⅰ类错误率都能控制在5%左右。各情形下两个Simon二阶段方法的效能差异不大，都能达到80%左右，在前3个情景中，贝叶斯方法的篮子设计效能均优于传统篮子设计，但缺点就是异质的情况下效能明显有所缩减，如情形4和5，效能范围在63.7%～74.3%，明显低于传统篮子试验的效能。

表1 传统篮子设计和贝叶斯篮子设计无效假设下拒绝率的比较

注：灰色区域表示一类错误；非灰色区域表示检验效能。

试验层数分别为3/5/10时不同篮子试验设计下至少拒绝一次无效假设的概率见表2，从表中可以看出单独使用Simon二阶段设计的传统篮子设计具有更高的整体假阳性率(即在至少一种肿瘤类型中实际无效的药物被认为有效)。比如，5个肿瘤类型且每个肿瘤类型具有10%假阳性率，一个无效药物被在一个或多个肿瘤类型中宣称为有效的概率高达40%以上，若肿瘤类型增多，假阳性率则更高，相比之下，贝叶斯篮子设计优势显现，既能借用层间信息，又能相对严格的控制整体假阳性率。

表2 传统篮子设计和贝叶斯篮子设计总一类错误的比较

不同篮子试验设计下的平均总样本量比较见图3，为了便于比较，我们分别设置不同试验组的最大总样本量为60/100/200。(A)～(C)图参数设置唯一的差异就是贝叶斯篮子设计指定的每次期中分析纳入人数不同，分别设置为5、10和20人。从图中可明显看到设置不同的期中分析人数，对贝叶斯方法的样本量有所影响，所以临床中要视实际情况而定。Simon二阶段方法计算出的平均总样本量差不多，优化方法计算出的样本量略高。如图3(A)，当每次期中分析纳入5人时，应用贝叶斯方法的篮子设计计算出样本量均小于传统设计，当每次期中分析纳入人数变多之后，应用贝叶斯方法的篮子设计样本量增多，但当试验层数和期中分析次数较多时贝叶斯篮子设计方法依旧是非常节省样本量的。

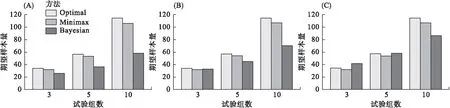
图3 传统篮子试验和贝叶斯篮子试验的平均总样本量比较

实例应用

众所周知，维罗非尼已经获批用于含有BRAF V600E突变的黑色素瘤患者，它是针对不同原发部位和组织学的多种癌症中的单一变异靶向药，从而定义了疾病特异的篮子设计。Hyman[5]等研究者纳入了122例携带BRAF V600E基因突变的患者，探索维罗非尼分别在非小细胞肺癌、卵巢癌、大肠癌、肝小胆管癌/胆管癌、乳癌、多发性骨髓瘤和其他实体瘤中的安全性和有效性，该篮子试验的初步临床疗效很可观，我们可以用贝叶斯方法去计算每个试验层反应率的后验概率。根据本文的模型，我们可以指定参数plo=0.15，phi=0.35，γ=0.5，λ=0.33，基于这些参数及实际数据，我们首先可以计算不同肿瘤亚组同质的后验概率Pr[H0|data]=0.0034，可见同质性不高，因此层间借用信息很少，但从后验概率的计算结果来看还是可以发现非小细胞肺癌、埃尔德海姆-切斯特病或朗格汉斯细胞组织细胞增生症、间变性多形性黄瘤反应率大于有效率0.35的后验概率分别是0.9787、0.9497、0.9067，可初步判断维罗非尼对其治疗有效，相反，在结肠直肠癌和神经胶质瘤中疗效并不理想。此外，胆管癌、甲状腺未分化癌、多发性骨髓瘤和其他种类的后验概率处于界值之间，所以疗效还不确定，需要进一步研究。有效的后验概率可能并不用在正式评估，但它便于总结反应率观察值和样本大小，而这些发现将也有助于未来研究的设计。

表3 维罗非尼治疗Braf V600阳性肿瘤篮子试验的反应率大于0.35的后验概率

讨 论

随着下一代测序和免疫治疗的不断发展，主方案(包括伞、篮子、平台试验)成为创新型临床试验的需求。篮子试验是主方案的一种，目标是研究多种疾病或疾病亚型下的单一靶向治疗[15]。越来越多的大型篮子试验如NCI-MATCH[7]、TAPUR[10]正如火如荼的进行着。篮子设计适用于靶向药物在早期肿瘤研究中的瘤种筛选以及以某一靶点为适应症的临床研究。早期肿瘤临床试验若采用篮子试验设计来评估试验中不同肿瘤患者的有效性和安全性，就会筛选出较有前途的瘤种进行确证性临床试验，从而提高早期肿瘤研发的效率。相同靶点的病人往往在不同瘤种所占比例非常低，若靶向药疗效好，不仅能提高临床研究效率，同时也能节约临床运营成本，使之尽早惠及患者，在控制医疗保健的社会成本方面发挥重要作用[3]。

在评估药物对不同组织学/分子变异亚组疗效时，人们有理由相信组间的临床活性存在某种程度相似，也越来越多考虑借用组间信息提高试验效率的贝叶斯方法的篮子试验理论研究[16]。很多研究者提出使用贝叶斯层次模型的方法，本文介绍的基于贝叶斯方法的篮子试验可以看作是二阶段设计从单臂向多臂的推广，也是层次贝叶斯方法的一种。理论上讲，使用结果自适应跨组借用很有吸引力，但专家经验表明采用贝叶斯层次模型的方法在10个或更少亚组的II期临床试验中可能不能有效的识别有反应的亚组[16]。对各适应症单独应用Simon二阶段设计[13]进行分析往往不能控制整体Ⅰ类错误率，从而导致无效适应症被继续研究，若通过多重校正提高各适应症检验水准来控制整体Ⅰ类错误率，则会导致样本量变大，而篮子试验大多是探索性II期试验，样本量通常较小，在这种情况下单独评估疗效是缺乏效能的[17]。本文介绍的基于贝叶斯方法的篮子试验操作灵活，对整体Ⅰ类错误的控制率更为严格，在识别出药物有足够的活性前分配较少的样本量，在试验层数较多情形下节约样本量，而且也可以推广到组间不同质的情形，但不同的先验选择会影响信息借用程度，应用局限于终点指标为二分类变量的非随机篮子试验，因此贝叶斯篮子设计的理论与应用还需要进一步探讨和研究。