混合型缺失数据填补方法比较与应用*

杨 弘 田 晶 王 可 张 青 韩清华△ 张岩波,3△

【提 要】 目的 针对混合型缺失数据，使用几种填补方法在缺失填补中的应用并评价填补效果。方法 结合实际数据，模拟出不同缺失比例(10%、20%、30%、50%)，采用MissForest、因子分析(FAMD)、K-最近邻填补法(KNN)和基于链式方程多重插补(MICE)四种方法进行填补；采用错分类比例(PFC)、正则化均方根误差(NRMSE)和回归系数估计值比较填补效果。结果 FAMD与MissForest相比，对分类变量填补表现优越。缺失比例是10%时，FAMD与MissForest表现优于KNN和MICE；缺失比例是20%时FAMD明显优于其它三种方法，但是MissForest表现亦可；缺失比例是30%时，四种模型表现明显下降，处理效果均不太理想；缺失比例是50%时，虽然FAMD仍有两个变量符合优良标准，但对某些变量估计误差较大，其它三种方法填补均失效。结论 FAMD填补方法总体表现较好，面对混合型缺失数据时可以考虑优先选用。

数据缺失在很多医学研究中是一个棘手的问题，在实际研究中，临床指标没有完全检测或有遗漏，缺失不可避免[1]。缺失会影响统计估计值的性质，如平均值、方差或百分比，导致估计效果降低和结论错误[2]。此外，许多传统的分析方法都依赖于完整数据集，即不允许有缺失值。因此，缺失数据的填补往往是数据分析中不可避免的一步。随着人们对缺失数据的深入研究，很多新的高效测量方法在缺失填补领域得到广泛发展，不仅可以处理变量数量可能超过观测值的高维多元数据，而且可以处理同时存在连续变量和分类变量的混合型数据(mixed-type data)[3]。本文针对基于临床诊疗数据中常见的混合型数据，在随机缺失(MAR)假设下采用MissForest、因子分析(factorial analysis for mixed data,FAMD)、K-最近邻填补法(K nearest neighbors imputation，KNN)和基于参数调整的链式方程多重插补(multivariate imputation by chained equations,MICE)对完整心衰电子病历数据进行缺失模拟并进行效果评价，为混合型缺失数据的填补应用提供依据。

原理与方法

对缺失值进行填补要尽量让填补值接近真实值，以避免对经填补后的数据集分析时与原始数据集分析结果产生偏差。因此，本文选用以下四种在研究中表现较好的针对混合型缺失数据填补方法应用于本研究。

1.MissForest 填补

缺失森林算法是基于随机森林的一种迭代填补算法，2012年由Stekhoven 首次提出使用，通过对许多未修剪的分类树或回归树进行平均，构成了一个多重填补方法[3]。其主要思想是假设一个数据X=(X1,X2,…,Xp) 是n×p维矩阵，仅使用数据集观察部分训练随机森林直接预测缺失值，该方法克服了传统随机森林要求响应变量必须是完整的这一缺点。本文中对MissForest参数设定为：ntree=500,mtry=3。

缺失森林填补过程如下：

(1)使用均值填补对数据X中缺失值进行初始预测；

(2)将变量XS,s=1,…，p依据缺失比例从小到大进行排序，对没有缺失的样本进行训练，并使用第一次拟合的随机森林进行填补；

(3)将训练好的随机森林应用于缺失部分数据，对缺失值进行预测得到一个填补矩阵；

(4)重复以上过程，直到满足停止标准，即新填补的数据矩阵与前一个矩阵之差首次增加时。

2.FMAD填补

因子分析(factorial analysis for mixed data,FAMD)是Audigier等人于2014年提出的一种专门针对混合数据进行描述、总结和可视化的填补算法。其基于主成分分析法，它的目的是研究个体间的相似性与变量间的关系(主要是连续变量与分类变量)，允许同时使用个体与变量间的关系来预测缺失值。FAMD的原则是平衡分析中连续变量和分类变量的影响，FAMD的原理是将分类变量转化为虚拟变量，并与连续变量连接起来。对每个变量进行加权，并同时考虑到不同类型的变量以平衡每个变量的影响，使各种类型的变量对主成分的构建都有同等贡献[4]。

FAMD填补过程如下:

(1)数据初始化：使用平均值(连续变量)和比例(分类变量)进行输入。计算标准偏差和列边距，从而计算连接矩阵的权重(连续变量和虚拟变量的指标矩阵)。

(2)迭代直至收敛：(a)对完成执行PCA加权数据矩阵进行参数估计。(b)用S维数拟合值对缺失数据填补。(c)更新连续变量的均值、标准差和分类变量的列边距。

3. KNN填补

本文中使用Troyanskaya等在2001年提出的KNNimpute算法，通过寻找离观测值最近的K个变量，并对这K个变量取加权平均，得到填补缺失的值变量Xj。因此，权重取决于变量Xj的距离[5]，本文中距离选择为欧氏距离。为了比较不同类型的变量，我们将数据中分类变量编码为{0，1}。由于选取不同K填补效果差异较大，我们通过试验最终确定K=5。

4. MICE填补

MICE多重填补是基于联合建模(joint modeling,JM)和链式方程(fully conditional specification,FCS)[6]。其基本原理是假设完整数据X是从含m个变量的多变量分布P(Y|θ)中随机抽取的观测值，通过观测数据的Gibbs迭代抽样建立关于缺失变量θ的后验分布(填补方程)，然后对每个缺失值多次填补，最终综合多个填补数据集做出最终的参数估计[6]。本文我们对MICE进行5次填补，对连续变量使用均值回归，分类变量使用逻辑回归。

模拟分析

1. 模拟思路

本文结合实际数据，模拟含有4个变量(Y,X1,X2,X3)的混合型数据集。X1和X3为连续变量，X2为二分类变量；结局变量Y(二分类)由X1,X2,X3共同定义。将X2作为辅助变量设定数据的缺失机制为随机缺失模式(MAR)。具体模拟过程如下。

X2依据有无高血压史设定比例为P(X2=1)=0.6；

2. 模拟完整数据集与模型构建

完整数据集均由Rstudio模拟获得，设定观察数为1000。基于完整数据集分别模拟缺失比例10%、20%、30%和50%的随机缺失模式(MAR)数据集，在同一缺失数据上分别采用FAMD、MissForest、KNN和MICE法进行填补，将得到的完整数据集与原始完整数据集进行比较，重复100次。

3. 评价指标

本文中采用两种指标来综合评价填补方法。对分类变量和连续性变量的模型评价分别采用错分类比例(proportion of falsely classified,PFC)和正则化均方根误差(normalized root mean squared error,NRMSE)[3]：

其中Xtrue是完整数据集矩阵，Ximp是填补后完整数据集矩阵。上述两个指标范围均为(0,1)，越接近0模型表现越好，越接近1则越差。

4. 模拟结果

由图1我们可以看出，四种方法随着缺失比例增大，对连续变量和分类变量填补误差也逐渐增大。从NRMSE来看，缺失比例在10%～30%时，FAMD与MissForest填补误差相差不大，两种方法均优于KNN和MICE；从PFC指标看，缺失比例为10%时FAMD的填补误差最小，相比其它三种方法优势明显。20%～50%缺失比例中，FAMD略优于另外三种方法。综合分析结果，FAMD对混合型数据的填补效果最好，MICE填补效果最差。

图1 不同缺失比例(10,20,30,50%)下四种方法(FAMD,MissForest,KNN,MICE)的NRMSE(上)和PFC(下)分布图

实例应用

1. 资料来源

在酶解时间、酶添加量和料液比均为上述试验中的最佳条件下，试验考察了酶解温度对辣椒碱、辣椒二氢碱及辣椒红色素含量的影响，试验结果见图3中A。

本研究资料节选自山西医科大学附属第一医院于2017年8月至2018年8月入院诊断为慢性心力衰竭的726名患者的部分电子病历资料为完整数据。根据左心射血分数的不同可分为射血分数降低的心衰(HFeEF)和射血分数保留的心衰(HFpEF)，不同类型的心衰治疗方式有所区别。经共线性诊断，数据中各变量方差膨胀因子(VIF)均小于2，可以认为共线性对本研究影响不大。基本情况见表1。

表1 完整数据各变量基本情况

2. 分析方法及评价标准

本研究采用前一种方式，对完整数据集构造不同缺失比例(726×8个数据点中缺失10%，20%，30%，50%)的随机缺失数据，使用四种方法分别进行填补，每种试验模拟10次。最后用填补后的数据与原始完整数据进行比较，依据评价指标来评价各填补方法效果。对于临床电子病历数据集，由于数据缺失的主要原因取决于数据收集中患者相关信息的可用性，缺失机制可视为随机缺失模式(MAR)[7]。数据分析均采用Rstudio 1.1.4，使用“missForest”、“missMDA”,“VIM”和“MICE”包进行填补。

为了评价填补数据的有效性[7]，我们以射血分数为因变量，其他变量为自变量建立二元logistic回归对数据进行统计分析，对原始数据进行建模，模型及各变量均有统计学意义。随后使用填补后的数据建模，通过对比各变量回归系数(β)及相对误差(θ=(β2-β1)/β1×100%)来评价填补后数据的有效性。

评价等级分别为：优(|θ|≤10%)、良(10%<|θ|≤20%)、中(20%<|θ|≤50%)和差(|θ|>50%)。评价标准为计算等级顺位累加构成比(优+良)，若构成比相同则参考相对误差的大小；若“差”则为填补失效。

结果与分析

1. 四种方法的NRMSE和PFC

NRMSE和PFC比较结果分别如图2、图3。单纯比较NRMSE，我们可以看到MissForest与FAMD在4种缺失比例下差异均无统计学意义，说明对连续变量填补效果表现无几，二者表现优良。但是MICE表现较差，NRMSE比前两者高将近10%。KNN表现居于中间。在分类误差PFC上，FAMD表现最优；MissForest与KNN分类效果相差不大，MICE分类误差最大。

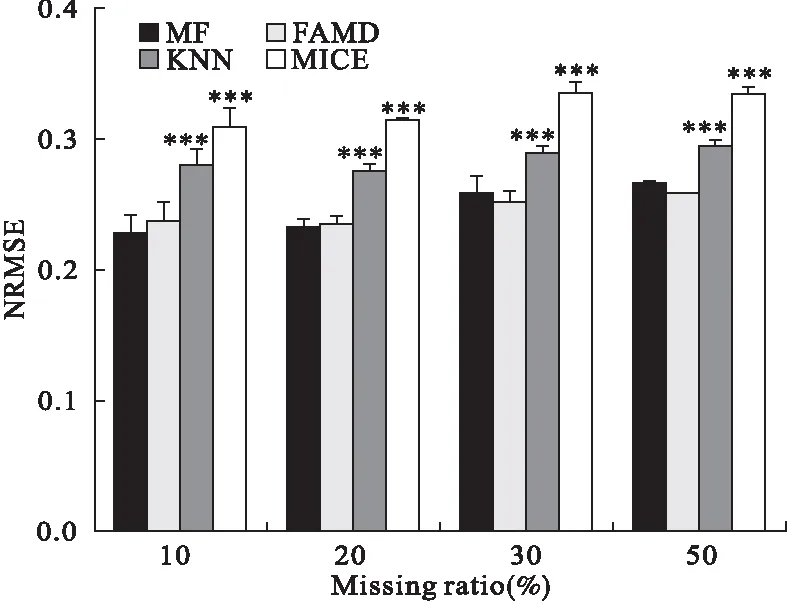
图2 不同缺失比例下四种填补模型的NRMSE

*：NRMSE为10次试验结果平均值；采用Wilcoxon配对t检验，FAMD(浅灰)、KNN(深灰)和MICE(白色)分别与MissForest(黑色)组进行比较；‘*’P<0.05,‘**’P<0.01,‘***’P<0.001

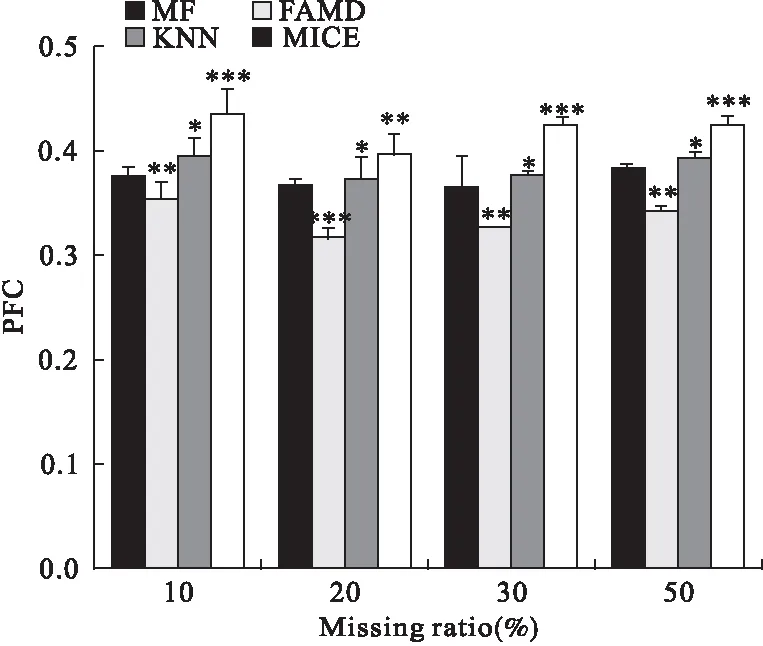
图3 不同缺失比例下四种填补模型的PFC

*：PFC为10次试验结果平均值；采用Wilcoxon配对t检验，FAMD(浅灰)、KNN(深灰)和MICE(白色)分别与MissForest(黑色)组进行比较；‘*’P<0.05,‘**’P<0.01,‘***’P<0.001

2. 不同缺失比例下变量的回归系数

建立二元logistic回归，缺失率是10%，在8个变量中，MissForest填补后回归系数符合优和良的标准分别为 3，3；FAMD填补后符合的为4，2；KNN填补后符合的为3，2；MICE符合的为0，4。四种方法中MICE相对误差与另外三种的相比较大，说明其填补后数据与真实数据相差较大。详见表2。

当缺失率是20%时，MissForest填补后符合回归系数的优良标准分别为2，1；FAMD分别为3和2；KNN分别为3，1；MICE分别为0，3。四种方法中除MissForest外，另外三种的填补符合优良的计数与10%缺失率时的变化较小，说明MissForest随着数据缺失的增加其填补效果不稳定，与沈琳等人的结论一致[8]。详见表3。

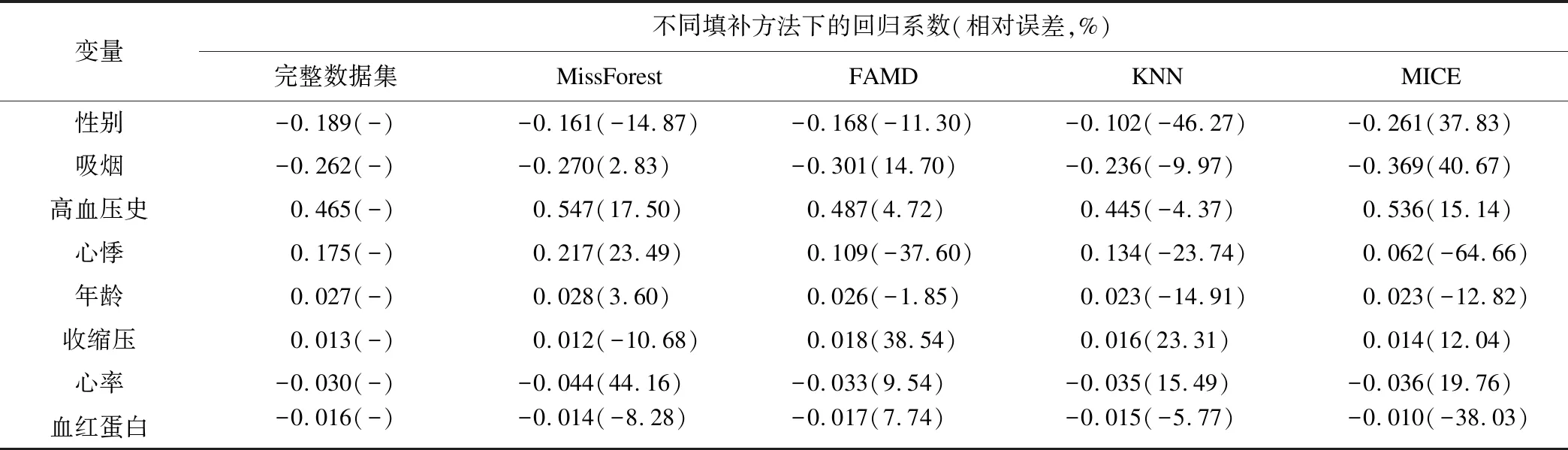
表2 10%缺失数据下不同处理方法的回归系数及相对误差

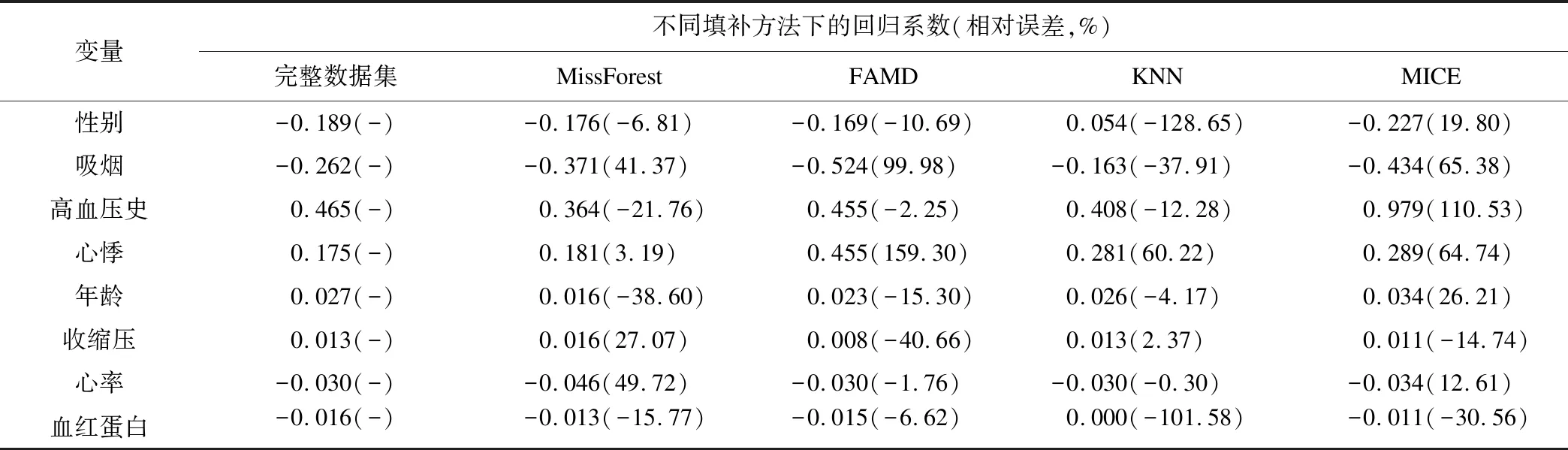
表3 20%缺失数据下不同处理方法的回归系数及相对误差

当缺失率为30%时，MissForest填补后符合回归系数的优良标准分别为1，1；FAMD分别为2，1；KNN分别为1，1；MICE分别为1，0，相比缺失比例为20%时总体模型表现均较差。详见表4。

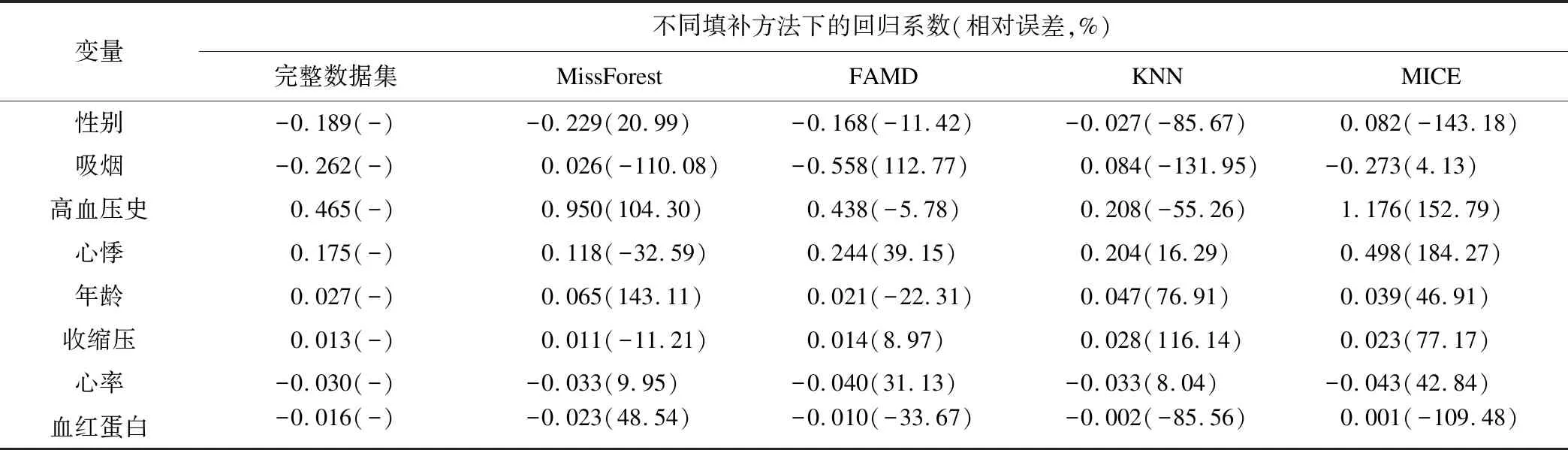
表4 30%缺失数据下不同处理方法的回归系数及相对误差

当缺失率是50%时，MissForest、KNN和MICE回归系数符合优良标准的均为0；但FAMD符合优良标准的分别为1，1。除FAMD外，另外三种填补方法回归系数的相对误差有一多半变量都超过50%，总体而言填补效果均不太理想，可以认为处理失败。详见表5。

表5 50%缺失数据下不同处理方法的回归系数及相对误差

讨 论

混合型数据是临床电子病历系统中最常见的数据类型。对于缺失数据有两种方法被普遍使用[9]：一种是删除对应缺失的所有变量或删除缺失对应的该患者所有数据；另一种是采用均值替代、临近值替代或连续分布情况下的EM算法等。这两种方法中前者会使数据信息丢失，后者无法进行混合性数据缺失值的填补，在做分析时产生偏差[10]。此外，缺失值在数据分析中也有诸多的不确定性。

本文在10%、20%、30%、50%不同缺失率下比较了MissForest、FAMD、KNN和MICE四种方法对混合型数据的填补效果。结果提示，针对混合数据，总体来说FAMD填补方法要优于其他三种方法，MICE表现最差。FAMD在不同缺失率下对连续变量的填补误差(NRMSE)与MissForest相差无几，但比KNN和MICE要低。分类变量的错分类误差(FPC)，在不同缺失率下，FAMD表现稳定且在四种方法中表现最优。在10%～30%缺失比例下，与MissForest算法比，在大多数情况下，FAMD算法对两种类型的变量具有更好的拟合能力，这与Audigier等人研究结论一致[4]。而MissForest总体表现要比KNN和MICE算法更优，这与Stekhoven等人结论也一致[3]。在数据缺失率达到50%时，FAMD达到优良标准分别为1、1，但是也有2个变量相对误差超过50%；而其它三种方法填补效果均无效，说明当缺失比例过大时，任何填补方法都是无效的，这与Enders CK等人结论一致[11]。

本次研究的数据仅仅来源于心衰患者电子病历部分变量的模拟缺失数据，数据量大小、数据维度、变量类型、变量比例等数据结构固定未变，对不同数据结构情形下的不同填补方法有待进一步比较。

总之，FAMD在本文中总体表现稳定，由于其可以很好的处理分类与连续变量之间关系，尤其是具有高度线性关系下表现亦优秀[12]，这种方法可以使研究人员从多维角度研究个体之间的相似性和变量间的关系，而且调用 ” missMDA” R包操作简便无需进行复杂的调参[13]，在面对复杂的混合型数据缺失填补时，不妨是一种可以优先考虑的方法。