矩阵初等变换在高等代数中的应用及教学研究

张 芳 英 朱 睦 正

（河西学院数学与统计学院，甘肃 张掖 734000）

矩阵初等变换是《高等代数》课程的一个重要组成部分，在该课程中有着特殊的地位与作用，其思想贯穿于高等代数的始终，是研究和学习该课程的一个重要工具和手段，在矩阵的理论研究中占有非常重要的地位.

1 矩阵初等变换在高等代数中的应用

1.1 求矩阵（向量组）的秩

矩阵（向量组）的秩是矩阵（向量组）的一个重要特征，是反映矩阵（向量组）本质的一个不变量.求矩阵（向量组）秩的常规方法是求极大无关组所含向量个数或求矩阵（向量组）最高阶非零子式的阶数，但这俩方法的缺点都是技巧性比较强，不能机械运算.下考虑矩阵初等变换法求矩阵（向量组）的秩.

定理1［1］若矩阵A 与B 相似，则.

步骤如下：

（1）矩阵行初等变换化矩阵A 为阶梯形矩阵B；

（2）阶梯形矩阵B 非零行的行数即为A 的秩.

矩阵行、列初等变换可单独亦可混合使用，因为矩阵的行、列初等变换都不改变矩阵的秩.

1.2 求逆矩阵

定义［1］如果n 级方阵A 和B 满足条件AB=BA=E，则称A 和B 均可逆且互为逆矩阵.

根据逆矩阵的定义，求矩阵A 的逆就是寻找矩阵B 使得AB=BA=E 成立.由于AA*=A*A= ||A E，取B=A*||A 则满足矩阵可逆定义的条件，从而是矩阵A 的逆矩阵，即A-1=B=A*||A .因为这里的A*是矩阵A 的转置伴随矩阵，此方法也被称为伴随矩阵法［1］.

根据可逆矩阵是有限个初等矩阵的乘积，一方面BA=E可视为对矩阵A 左乘可逆矩阵B（系列初等矩阵），即对矩阵A 进行系列行初等变换；另一方面AB=E 亦可视为对矩阵A 右乘可逆矩阵B（系列初等矩阵），即对矩阵A 进行系列列初等变换［2］.

特别注意，对A 左乘可逆矩阵B 时没有右乘任何矩阵，所以进行行初等变换时不能进行列初等变换.对A 右乘可逆矩阵B 时没有左乘任何矩阵，所以进行列初等变换时亦不能进行行初等变换.

解 对矩阵( )

A,E 进行行初等变换，

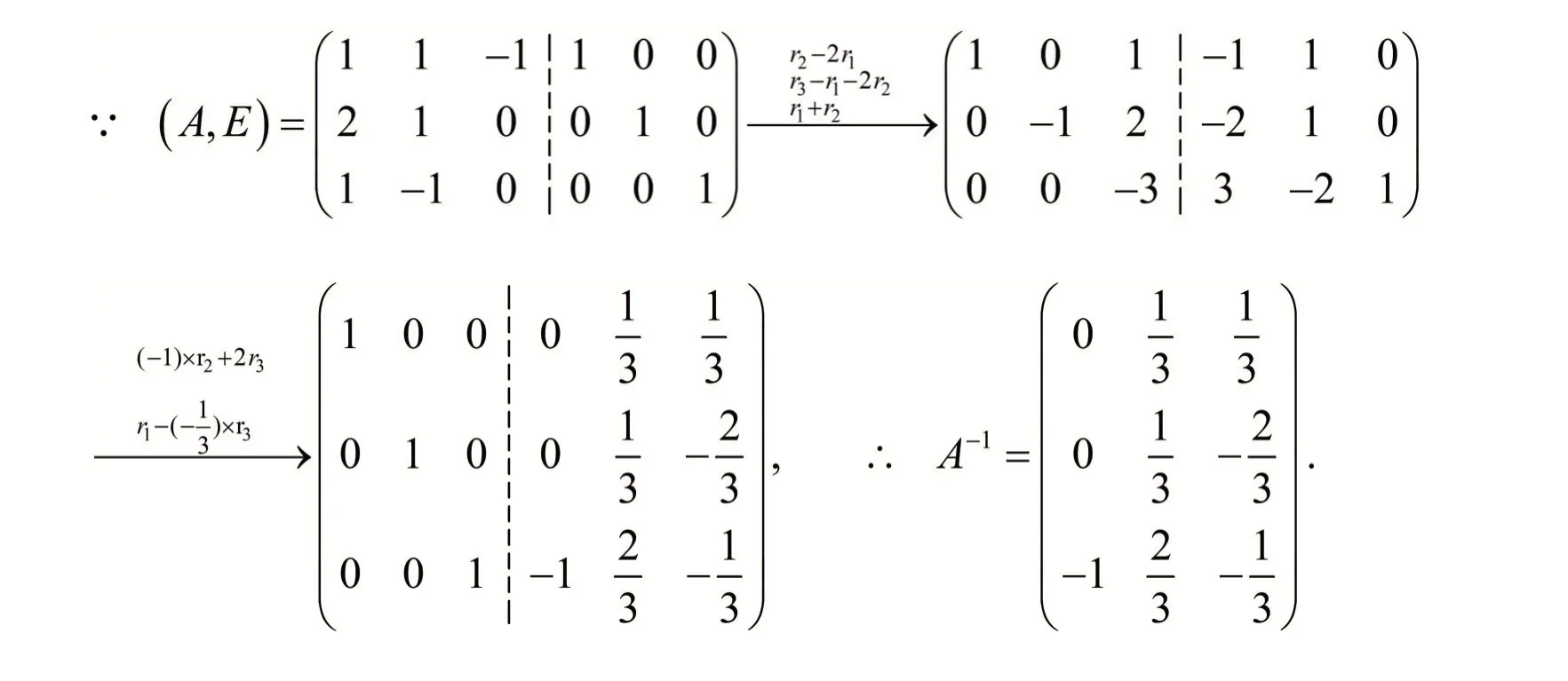
相比伴随矩阵法，矩阵行初等变换法求逆矩阵更加简单.因为伴随矩阵法求矩阵的逆时，矩阵阶数越高，要求的代数余子式就越多，从而运算量就越大，而初等变换只需要进行行初等变换即可.特别注意，不能使用矩阵列初等变换.

1.3 求解线性方程组

用消元法解线性方程组，实质就是将它的增广矩阵经过一系列行初等变换化为阶梯形矩阵.

解 利用行初等变换将增广矩阵化成阶梯形，则

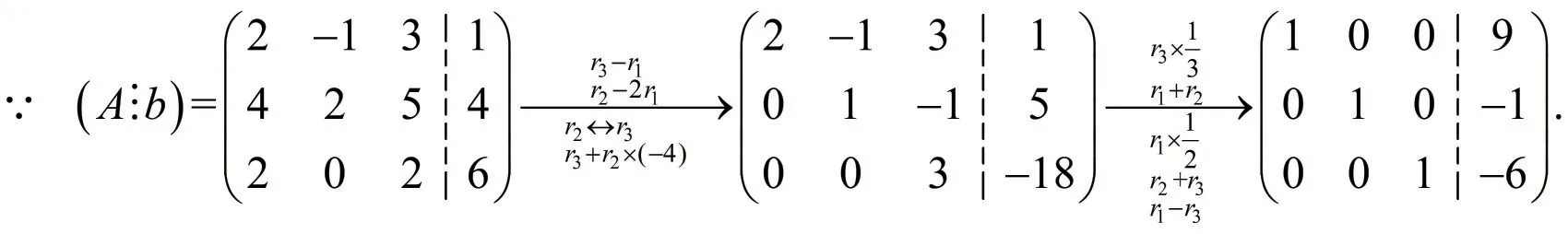
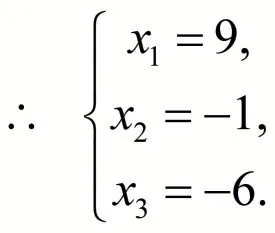
相比消元法，矩阵初等变换法求解线性方程组更加直观和简洁，不需要未知量直接参与运算，只需要对增广矩阵( A⋮b) 施行行初等变换.同时，线性方程组的解其实是常数列向量由系数矩阵列向量线性表出的系数，绝对不能施行列初等变换，即要抓住矩阵（向量组）初等变换的本质.

1.4 解矩阵方程

例4［4］求矩阵方程AX=B 的解，其中

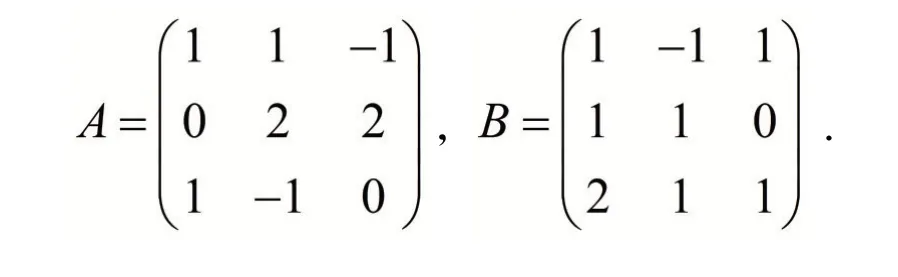
解 构造3行6列的矩阵并施行行初等变换

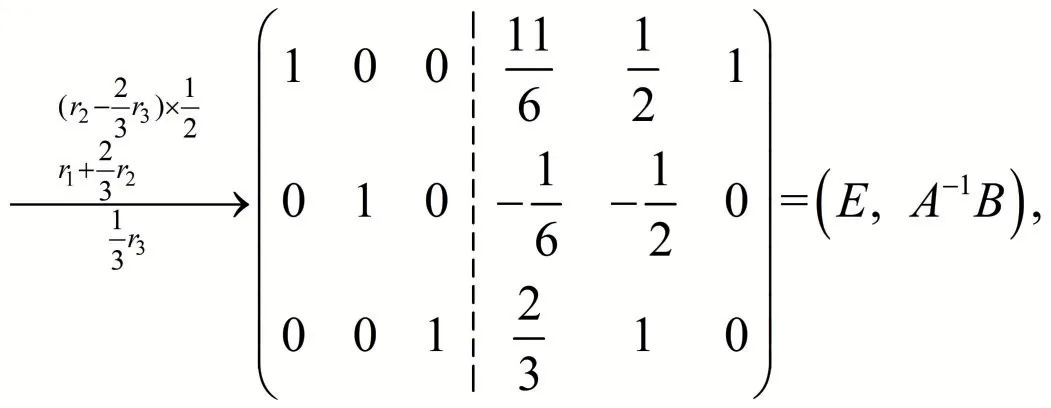
矩阵方程AX=B 的解为

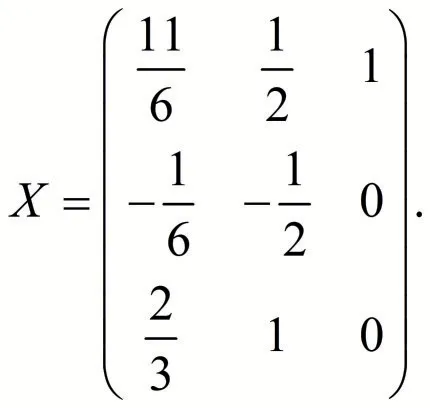
利用矩阵初等变换解决有关问题时，要改变行、列初等变换对等思想，应根据实际情况尽量强调“列向量，行变换”.这里类似于增广矩阵进行行初等变换求线性方程组的解，要绝对避免矩阵的列变换.

1.5 化二次型为标准形

定理3［1］任意二次型f=(x1,x2,…,xn)=XTAX 一定可以通过非退化线性替换X=CY 化为标准形.

根据定理3，可以得到化二次型的矩阵为对角矩阵的初等变换法：

例5［5］将二次型f=+2+52x1x2+6x2x3化为二次标准型.

解 令

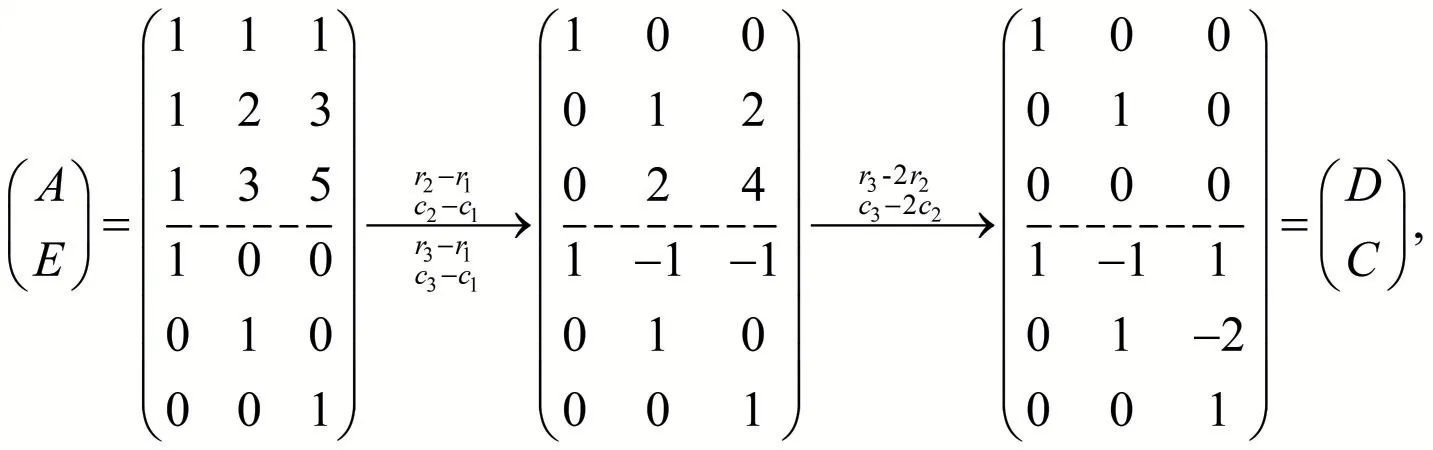
其中

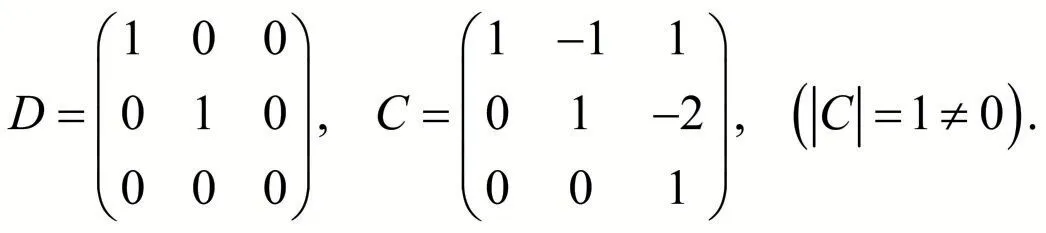
C 为线性替换矩阵，所作的非退化线性替换为

特别注意，由于是合同变换，行、列初等变换必须同时使用.

1.6 化基为标准正交基

施密特正交化方法［1］是化基为标准正交基的基本方法，但该方法计算繁琐，运算量大.下面利用矩阵初等变换法解决［6］.

设欧氏空间Rn的一组基是

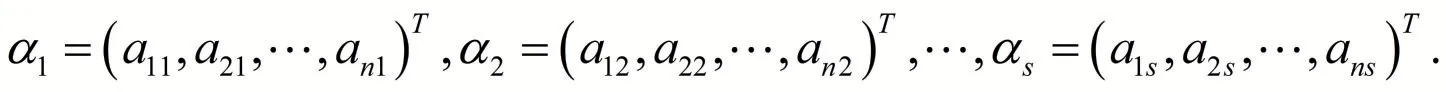
令A=( α1,α2,…,αn)，则ATA是一个n 阶正定矩阵，必与E 合同，存在n 阶可逆矩阵Q，使得QT( ATA) Q=(QTAT)( AQ )=E，即ATA 合同于单位矩阵且AQ 的列向量组是Rn的一个标准正交基.从而，得到利用矩阵初等变换法化基为标准正交基的方法

则AQ 的列向量组即为所求的标准正交基.

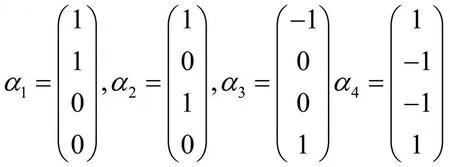
解 设A=( α1,α2,α3,α4)，则

利用( η1,η2,η3,η4)=( α1,α2,α3,α4)Q，可得所求标准正交基为

相比施密特正交化方法［1］，矩阵行初等变换法更为直观且计算量小.

2 矩阵初等变换的教学建议

2.1 讲明原理，说清方法

教学的目的是抓住复杂内容的实质，梳理核心思想和思路，讲明白原理，说清楚关键的步骤和具体的做法.例如，求矩阵A 的逆矩阵就是寻找可逆矩阵B 使得AB=BA=E，将矩阵B 视为系列初等矩阵的乘积，从而引入行初等变换或列初等变换，进而说明二者绝对不可以同时使用.

2.2 紧扣矩阵初等变换本质，强调“列向量，行变换”［6］

矩阵初等变换的本质是向量组的等价.例如，线性方程组的向量理解就是常数列向量能否写出系数矩阵列向量的线性组合，组合系数就是方程的解.对增广矩阵进行行初等变换实际上就是在寻找矩阵列向量的极大无关组，直观理解就是消元法，所以矩阵列初等变换是不合适的.

2.3 多做练习，加深理解

学好数学最好的办法莫过于动手做题，高等代数也不例外.通过具体的例子去理解抽象的定义和证明，将定理的结论运用到具体的例子中，从而加深对概念、定理和方法的理解和掌握.良好的解答证明题的能力是学好高等代数的重要标志之一.

3 总结

矩阵的初等变换是高等代数课程的重要组成部分，其思想贯穿于高等代数的始终.本文讨论了矩阵初等变换在高等代数中矩阵的秩、矩阵的逆、二次型标准化和标准正交基等问题中的应用，并就该知识点的教学策略进行了一些探讨.教师在教学工作中应当讲明原理，说清方法，强调行列初等变换的区别，有针对性地让学生做一定练习以便进一步理解矩阵初等变换的思想，提升灵活应用矩阵初等变换法简化或解决实际问题的能力，夯实专业理论基础.