用表面张力实验简单分析气体模型

葛 素 红 马 喜平 孙桂 华，2 王 新星，2

（1.河西学院物理与机电工程学院；2.河西学院物理与机电工程学院理论物理研究所，甘肃 张掖 734000）

1 引言

热力学的一个主要任务是研究热力学系统在所发生的与热现象有关的过程中所体现的物质性质和规律.最简洁和有效的方法，就是确定物质体系的物态方程.人们获得物态方程有效的办法是实验地总结和验证，这就使得良好物态方程的获得在实际中很困难，到目前为止，理论上得到的最好、最精确的物态方程就是理想气体状态方程，它可以用来处理各种过程中气体物性的分析研究，但在实际的生产和生活之中，是不存在理想气体的，实际中人们所接触到的，都是实际气体.而且，人们所呼吸的空气，不只是实际气体，它是实际气体的混合物.

1662年英国科学家玻意耳、1679年法国科学家马略特分别对给定量的稀薄气体在等温过程中的性质进行了实验研究，得到了稀薄气体的等温定律［1］.1802～1809年法国化学家、物理学家盖·吕萨克发现了稀薄气体的热膨胀定律，而在此之前的1746～1823 年间法国物理学家查理就发现了稀薄气体在体积不变的条件下，其压强随温度的变化作线性改变的实验规律［2，3］.这就是著名的气体实验三定律，经过人们在实验和理论上的分析认为，压强很小的稀薄气体，其宏观性质与气体种类没有关系，因此，把满足实验三定律的气体称为理想气体.到1834年法国物理学家和土木工程师克拉珀龙将气体实验定律归纳为理想气体状态方程.若气体系统平衡态参量为P、V、T，系统物质的量为n，R为普适气体常量，则其状态方程表示为［1］：

1801年英国化学家、物理学家道尔顿提出了混合气体分压定律，为我们研究空气的性质提出了可贵的理论依据.他认为同温度同体积的条件下，混合气体的压强等于相同条件下各种气体分压强的求和［1］：

当把气体看成理想气体，就意味着忽略了气体的个性，从微观上来分析，就意味着所有种类气体分子的大小都被忽略了，同时，也忽略了气体分子之间还应该存在的相互吸引的作用力.1873年荷兰物理学家范德瓦耳斯根据这两点提出修正，给出了一种实际气体状态方程［1］：

其中a和b分别是气体分子体积和分子间吸引力的修正参数，它们与气体种类有关，不同气体分子的这两个参数是不相同的，一般地这两个参数由相关实验来确定.

1901年在研究永久性气体的液化时，荷兰物理学家昂内斯将稀薄气体以体积展开，给出了另一种实际气体状态方程［4］：

如果只考虑二级修正，方程式如下：

其中B是第二位力系数，斥力对其贡献为正，引力对其贡献为负.比较（4）和（5）式可以认为范德瓦耳斯方程是展开到二级近似的昂内斯方程，由此可以认为，对于压强不太大的气体，温度较高情况下，分子间引力对气体的性质影响很小，这时主要是分子发生碰撞时的斥力起主要作用.而当温度较低时，情况则刚好相反.通常情况下，在300K左右，第二位力系数为负，说明分子间引力对气体性质的影响较斥力更加重要.这从另一个侧面说明了范德瓦耳斯方程只考虑分子间引力修正具有一定的正确性和适用性.

由于范德瓦耳斯方程是对实际气体的逼近，其气体参数的获得主要依赖于气液相变过程中临界点状态参数的测量.因此，到目前为止单独的关于范德瓦耳斯气体参数的研究文献未见报道.而在液体的表面张力现象的研究中有一个结论，我们可以通过测量球形肥皂泡的液体表面张力系数σ 和肥皂泡的半径r来计算球形肥皂泡内外的压强差［1］：

其中σ 是液体的表面张力系数，r是肥皂泡的半径.肥皂泡内外都是混合气体.基于（6）式本文设计实验测量了肥皂泡的表面张力系数和半径，计算获得其内外压强差，这个差值与肥皂泡内外气体特性有关，可以此来推算肥皂泡内外气体的特性.

2 实验结果与讨论

2.1 实验原理和用具

在液体与气体交界面处液体表面存在着一个薄层，这个薄层通常称作液体的表面层.由于物质的微观结构在这个薄层处与气体内部和液体内部的情况都不相同，在这个薄层处就表现出一种特殊的表面现象，即表面张力现象.这种特殊的现象使自然界更加色彩缤纷了，出现了很多有意思的景观，五颜六色的肥皂泡泡就是表面现象的一种.而泡泡正是由于液体的表面张力而形成的.经过实验验证液体的表面张力等于表面张力系数与周界长度的乘积，因此，在给定的实验条件下，表面张力系数σ 就表示其单位长度上的表面张力.

本实验应用力敏传感器比较全面地测量不同液体的表面张力系数.实验主要装置是FD-NST-I型液体表面张力系数测定仪.它的主要结构原理是量程范围较小、灵敏度高且稳定性较好的硅压力敏传感器张力测定仪，测量液体的表面张力.将圆环状金属片吊挂在灵敏的测力计上，然后把它浸入到待测液体中，当缓缓移动高低位置时金属圆环就会拉出一层与液体相连的液膜，由于表面张力的作用，与金属环相连的力敏传感器张力测定仪就会显示出液膜拉断前一瞬间数字电压表读数U1和液膜拉断后一瞬间数字电压表读数U2.由于液膜有两个表面，在一级近似条件下，可以认为脱离力为表面张力系数乘上脱离表面的周长，即［5-7］：

D1和D2分别为圆环的内径和外径. σ 为液体的表面张力系数.

硅压力敏传感器由弹性梁和贴在梁上的传感器芯片组成，其中芯片由四个硅扩散电阻集成一个非平衡电桥，当外界压力作用于金属梁时，在压力作用下，电桥失去平衡，此时将有电压信号输出，输出电压大小与外力成正比，即

式中，F 为外力的大小， K 为硅压力敏传感器的灵敏度，ΔU 为传感器输出的电压差值大小.把（3）式和（4）时代入（2）式，即有：

对力敏传感器张力测定仪定标之后就可以用作图求斜率的方法求出灵敏度K 值，所以，只要测定液膜拉断前一瞬间U1值和拉断一瞬间值U2，计算出差值，即能得出液体表面张力系数σ 值.本实验在同一实验室用同一台仪器，首先定标得到仪器的灵敏度K值为3.616mv/N.

2.2 市售泡泡液中加入不同物质组成混合溶液的表面张力系数及其吹出泡泡半径的测定

表1 市售泡泡液中加入食盐组成不同浓度的混合溶液的表面张力系数Tab.1 surface tension coefficients of bubble liquid of salt

在给定温度条件下，测量不同浓度混合溶液的表面张力系数，获得可以吹出泡泡的不同表面张力系数的溶液和其对应的表面张力系数，数据在表1和表2中列出.溶液的配制是以食盐（中盐甘肃省盐业集团有限公司售）和白糖（市售散装）为溶质，以市售的一种泡泡液（型号：MG952，汕头市澄海区金钿玩具有限公司产）为溶剂，按照质量百分比配制50g不同浓度的混合溶液，根据定义式：

称量相应质量的食盐、白糖后，与相应质量的泡泡液混合后，将食盐和白糖分别加入到盛有泡泡液的烧杯中并用玻璃棒充分进行搅拌，待食盐和白糖完全融化后静置即可得到相应浓度的溶液.

表2 市售泡泡液中加入白糖组成不同浓度的混合溶液的表面张力系数Tab.2 surface tension coefficients of bubble liquid of sugar

市售泡泡液吹出的泡泡在空气中飞翔，由于其自身重力的影响，实际上不会是标准的球形，但可以粗略地看作是一个球体.由于吹出的泡泡不易固定而且极其容易破裂，因此对于其半径的测量，存在很大困难.2016年姜仲篪等人在研究泡泡大小与张力系数时用拍照对比方格纸的方法粗略测得了吹出泡泡的直径，这种方法较为简单且容易操作，但须两个人来完成［8］.本实验中设计了一种简单易行的测量方法，是用吸管在光滑平整的桌面上吹出半个泡泡并直接测量了泡泡的半径.为了使得所吹出的泡泡达到最大状态，在吹泡泡之前，先用泡泡液将桌面润湿，增大泡泡表面与桌面的润滑程度.同时为了方便测量泡泡的高度，需将刻度尺竖直固定在桌面上，然后用吸管蘸取少量泡泡液，在湿润的桌面上吹出半个泡泡，同时目光平视泡泡凸起面所对应的刻度尺上的高度，当泡泡炸裂的瞬间，读出该时刻泡泡凸起面所对应的刻度即为该浓度（表面张力系数）下所吹出的最大泡泡的半径，为了减小误差需要多测量求取平均值，本次实验在每一浓度下测量五次.

测量所得同浓度的食盐混合溶液和白糖混合溶液的所吹出泡泡的半径和对应的表面张力系数在表3和表4中列出.根据研究，液体温度对液体表面张力有很大的影响［9-11］，而我们的实验没有能力统一测量时的环境温度，因此，需要对表3和表4中所测量的表面张力系数数值进行修正.人们对纯水表面张力系数研究比较广泛，依据纯水在0℃～100℃之间的表面张力系数测量值，拟合获得了其表面张力系数随温度变化的经验函数［12］，不同温度下纯水的表面张力系数如表5所示.但从物质的热学形态上考虑，当温度远低于常温时，水的凝聚态更强，而当温度达到35℃以上时，表面蒸发现象也很明显.本文实验是在常温下做的，上下温差不超过5℃，因此，选15℃～30℃为最佳温度段，拟合得到纯水的表面张力系数随温度升高而降低的一级近似梯度为：0.155×10-3（N/m）.以此为温度修正因子修正不同温度下混合溶液的表面张力系数，并在表3和表4中第二行列出（以21℃为基准）.

表3 市售泡泡液中加入食盐组成不同浓度的混合溶液吹出的泡泡半径Tab.3 The bubble radius of the bubble liquid of salt

表4 市售泡泡液中加入白糖组成不同浓度的混合溶液吹出的泡泡半径Tab.4 The bubble radius of the bubble liquid of sugar

表5 各温度下水的表面张力系数的公认值Tab.5 surface tension coefficients of water

2.3 泡泡内外压强差及空气的模型分析

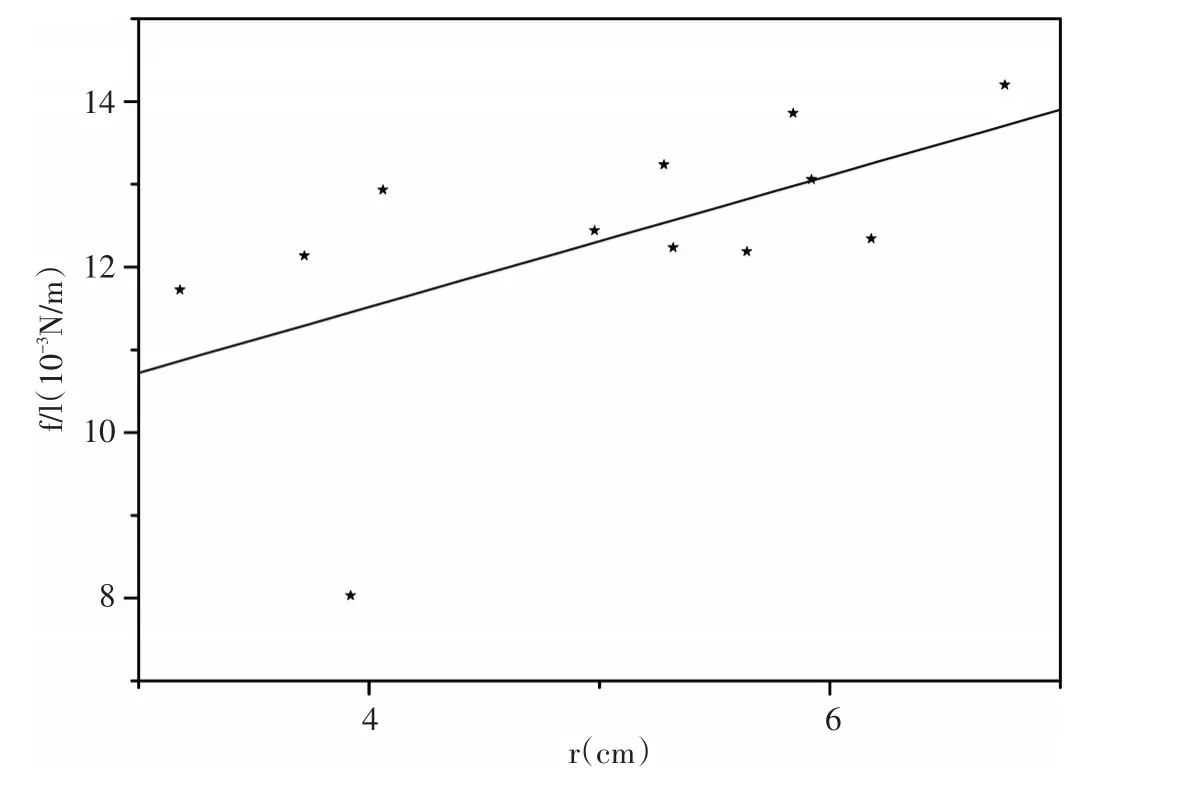
图1 市售泡泡液中加入食盐组成不同浓度的混合溶液的表面张力系数与其泡泡半径相关曲线Fig.1 The relation between bubble radius and surface tension coefficient of Salt solution

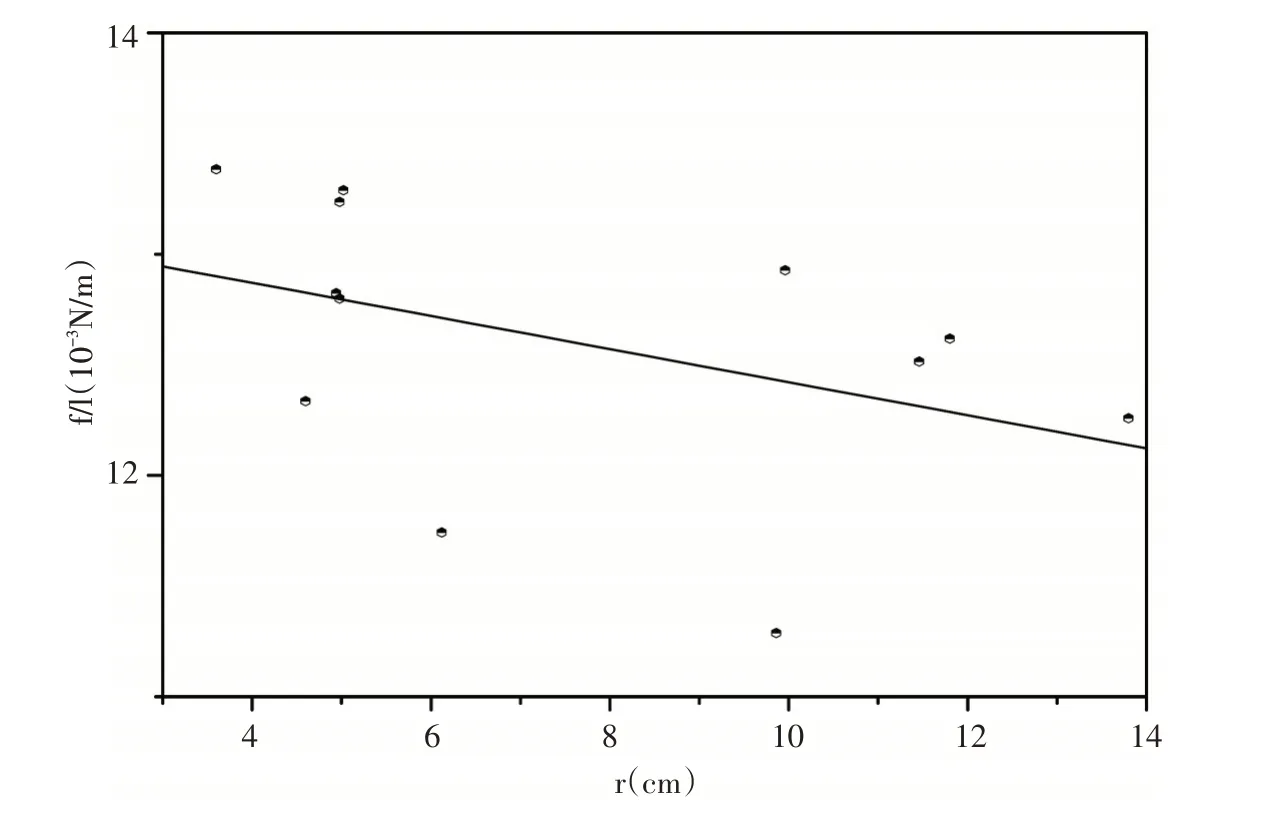
图2 市售泡泡液中加入白糖组成不同浓度的混合溶液的表面张力系数与其泡泡半径相关曲线Fig.2 The relation between bubble radius and surface tension coefficient of sugar solution

表3和表4中列出的测量所得同浓度的食盐混合溶液和白糖混合溶液的所吹出泡泡的半径和对应的表面张力系数的修正值，绘制表面张力系数σ 与泡泡半径r的相关曲线如图1和图2所示.根据拟合结果，图1 给出的斜率值为0.79444，而图2 给出的斜率值为0.0748.依据公式（6）.按照图1所显示的，我们可以认为球形肥皂泡内外压强差的实验值为：

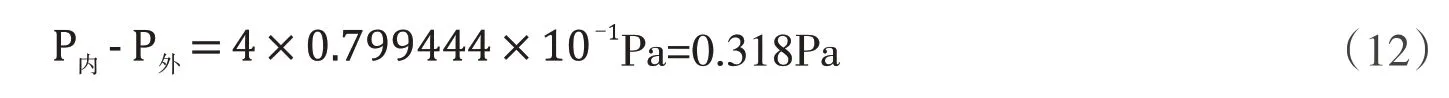
按照图2所显示的，我们可以认为球形肥皂泡内外压强差的实验值为：0.029Pa.

张掖市甘州区的大气压强，就是肥皂泡所处环境的外部压强.它的数据的获得有两种方法，第一是调查张掖气象数据，可知其年平均气压是852.0hPa.第二是根据等温气压公式来计算其数据［1］：

式中p（0）是零海拔的气压，即为一个大气压，M 是空气的摩尔质量，其数值为29；T 为空气的温度，本文设置为21℃（即所有的液体表面张力系数经过修正后表达为21℃的结果）；Z为张掖市甘州区的海拔，其数值为1467m.重力加速度g取张掖地区的数值为9.7807m/s2［13］.将数据代入（12）式，可计算得到张掖市甘州区的大气压强理论数据为：85190Pa，与气象数据相差不大.

肥皂泡内的气压也可以有两种算法，第一是当作理想气体处理，则其内部气压可以根据（14）式建模计算.肥皂泡内部是人体吹出的气体，将其看作理想气体，并认为经过呼吸道的降温作用，其温度与环境温度相同为21℃.人体呼出的气体主要为氮气（占78%）、氧气（占16%）和二氧化碳（占6），其密度按比例计算为1.32kg/m3，摩尔质量为30g/mol.计算的气泡内压为106859Pa，大于一个标准大气压.

由（13）式和（14）计算所得球形肥皂泡内外压强差很大，为21.669kPa，与实验测量的结果相差四个数量级，这显然是不合理的.虽然实验测量有误差，但在一定程度上反映了客观事实，因此，本文认为，将环境大气和球形肥皂泡内的气体当成理想气体模型来处理是不符合实际的.

用实际气体模型来处理，则是利用（3）式范德瓦耳斯方程，对于单位摩尔数的实际气体，（3）式可改写为：

若将肥皂泡内外的气体都看作是稀薄的（只考虑分子间吸引力）的气体，它们由于气体分子体积所产生的修正参数b基本上是相同的，因此，引起内外压强差的主要部分是由压强参数引起的，可以根据（15）式，对单位体积的气体，获得一个计算肥皂泡内外压强差的简易公式：

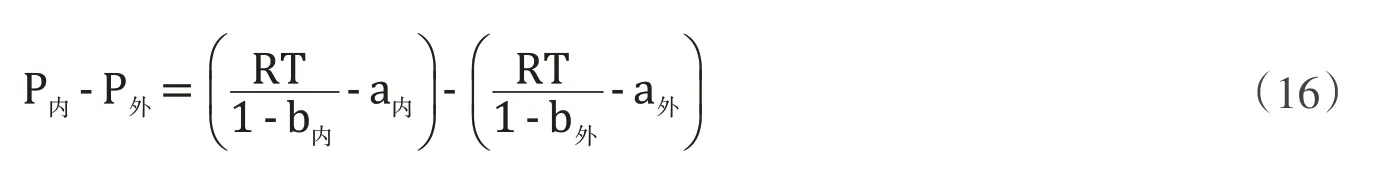
泡内气体为人体呼出的气体，泡外气体为张掖地区的空气，空气的组成主要为氮气（占78%）、氧气（占21%）、氩气（稀有气体主要是氩气，就当成氩气处理，占0.94%）、二氧化碳（占0.03%）和水蒸气（占0.03%）.取1mol单位体积的气体，由于体积参数的影响几乎可以忽略，只考虑压强参数的影响.各种气体的范德瓦耳斯压强参数a和体积参数b在表6种列出，根据表6参数和气泡内外气体的组成比例计算可得气泡内外压强差为：0.0133Pa.与实验测量的结果0.318Pa 和0.029Pa 相比较，这个数值只相差一个数量级，比较接近.因此，可以认为，无论是张掖地区的大气，还是人体呼出的气体，其实际模型都更接近范德瓦耳斯气体，距离理想气体这个简化模型很远.

图6 气体的范德瓦耳斯参数Fig.6 Van der Waals parameters of gas

3 结论

本文实验测量了将食盐和白糖加入市售泡泡液之中配制成的不同浓度的泡泡液的表面张力系数的大小，以及用不同的表面张力系数值的泡泡液吹出的泡泡的半径.根据热力学理论，球形肥皂泡的表面张力系数与其泡泡半径的比值与球形肥皂泡内外压强差成正比.在将球形肥皂泡内外气体看成稳定气体的情况下，可以用这个比值来推算球形肥皂泡内外压强差.经过实验和理论分析，本文发现：

1）在市售泡泡液里加入食盐和白糖，随着溶质的浓度的增大，泡泡液的表面张力系数呈下降的趋势.

2）泡泡液的表面张力系数小于11×10-3N/m时，吹出泡泡的半径已经比较小，即这个数值是良好泡泡液的一个临界值.本实验中市售泡泡液的表面张力系数的测量值是14.169×10-3N/m，可以认为这个数值是泡泡液表面张力系数的最佳值.

3）由于目前测量泡泡液的表面张力系数和泡泡液的半径均存在较大的系统误差，本文仅能给出定性的一个结果.根据本文实验测得泡泡液表面张力系数与其半径的比值计算可得泡泡液内外压强差的数值约为0.318Pa或0.029Pa，即肥皂泡内外压强差的数值范围0.1～0.01Pa，是一个很小的值域.这也说明，肥皂泡的平衡是非常容易被破坏的.

4）若把肥皂泡内外的气体看成理想气体，用理想气体模型理论计算肥皂泡内外压强差，其数值为21.669kPa.与实验数值相差6到7个数量级，显然，把肥皂泡内外的气体看成理想气体是不合理的.

5）若把肥皂泡内外的气体看成实际气体，用范德瓦耳斯气体模型理论计算肥皂泡内外压强差，其数值为0.0133Pa，是在实验数值的范围内.因此，本文认为，在张掖这个海拨1400m 的地区，用范德瓦耳斯气体模型来处理实际气体，是合理和可行的.