基于随机过程的粒子群改进算法
2020-06-28罗庆仪李秦
罗 庆 仪 李 秦
(兰州交通大学数理学院,甘肃 兰州 730070)
1 引言
粒子群优化算法(Particle Swarm Optimization,简称PSO)在Reynold 所提出Boids 模型[1]启发下,由Eberhart和Kennedy提出的一种新型群智能优化算法[2].该算法的本质是一种随机并行搜索算法,能以较大的概率收敛于全局最优解,且结构简单,操作方便,易于编程实现.自PSO提出之日,便得到了许多学者的关注,并通过不断的改进,现已成功应用到许多实际问题中,如锂电池建模[3],图像分割[4],优化控制[5]等等.然而,PSO算法具有容易陷入局部最优解和早熟的缺陷,为了克服这些不足,学者们通过对参数的调整,改进搜索方法以及增加辅助策略来改进PSO算法,如通过改变惯性权重[6]增加全局扰动[7]进而提高全局搜索能力,通过改进静止的粒子的位置选取方式[3]避免陷入局部最优的情况,还有一些与其他群智能算法融合的改进方法,如粒子群算法与遗传算法、模拟退火算法、差分进化算法等的结合[8]. 本文提出一种基于随机过程的粒子群优化方法(Stochastic Process Particle Swarm Optimization,简称SPPSO).仿真实验结果表明,在寻优精度,收敛速度,寻优正确率等方面SPPSO算法具有优越性.
2 基本PSO算法
PSO 算法中,将优化问题在搜索空间中的潜在解定义为粒子,所有粒子都有一个由目标函数所决定的最适值,每个粒子由自己的速度矢量决定自身的飞行距离和方向.粒子最开始在搜索空间中随机产生,通过追寻自身找到的最优位置和整个种群找到的最优位置,在解空间中通过不断的迭代更新自身位置,找到最优位置即最优解.
假设在D 维的搜索空间中,有N 个粒子组成一个种群,其中第i 个粒子在第t 步迭代时的位置描述为:
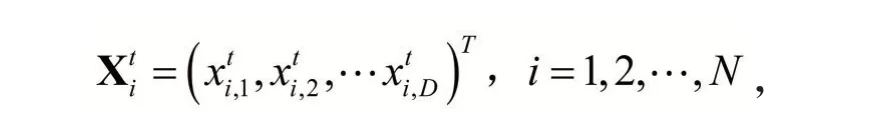
第i 个粒子在第t 步迭代时的速度描述为:
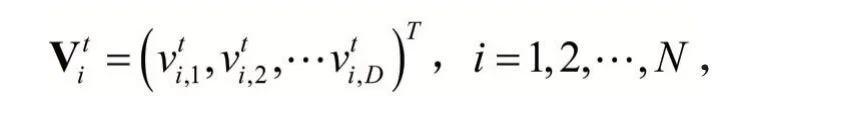
第i 个粒子在第t 步迭代为止搜索到的自身最优位置即个体极值描述为:

整个种群到目前为止搜索到的最优位置即全局极值描述为:
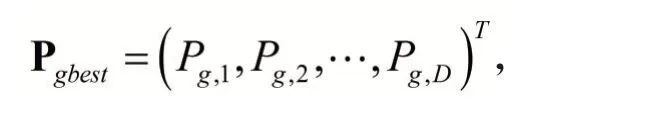
在搜索到个体极值与全局极值之后,粒子通过如下公式更新自己的位置和速度:
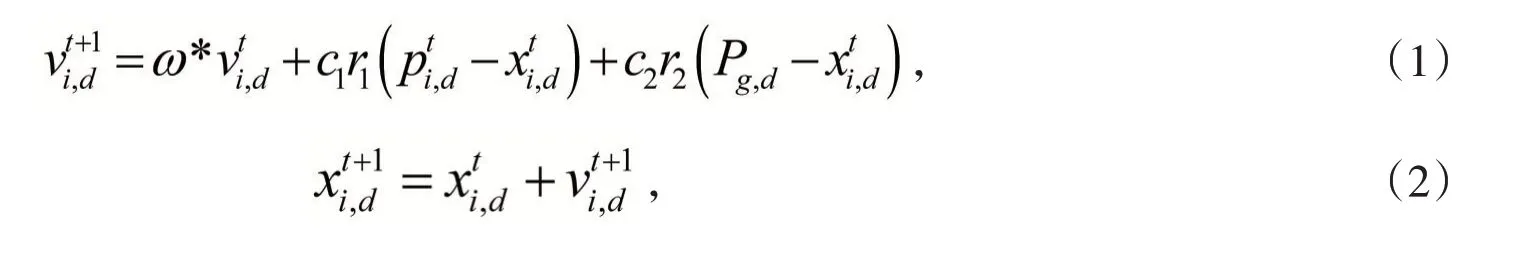
其中i,d 为第i 个变量在d 维上的分量,c1和c2为学习因子,r1和r2是服从区间[0,1]上均匀分布的随机变量.
式(1)右端由三项和组成[9]:
第一项“惯性”部分,反应了粒子在运动时候具有惯性,即有保持粒子自身先前速度的运动趋势,其中ω 称为惯性权重,反映了粒子局部和全局的搜索能力[10].在搜索前期,粒子需要在整个解空间快速搜索,即要求全局搜索能力要强,粒子原有的速度占比就应该大一些,到了搜索后期,粒子的搜索空间会大幅度缩小,那么对局部搜索能力的要求增大,粒子原有的速度占比就应该要小一些.目前关于惯性权重选择的研究已有不少文献,如自适应权重法、随机权重法、线性递减权重法[8]等等,本文采用的是线性递减权重法,具体描述公式如下:

其中ωmax和ωmin分别表示最大和最小权重值,k 表示当前迭代步数,k_max 表示最大迭代步数.
第二项“认知”部分,反映了粒子对自身最优位置的记忆,代表粒子对自身历史最优位置的置信程度,并且有向该位置逼近的趋势.
第三项“社会”部分,反应了粒子与粒子之间的经验共享和知识交流,代表粒子对种群最优位置的置信程度,并且有向该位置逼近的趋势.
正如式(1)和式(2)所描述,基本粒子群算法单纯的依赖整个种群的全局最优个体的指导,在解空间搜索最优解,常常容易陷入局部最优解和早熟的情况[11].
3 SPPSO算法
针对粒子群算法容易陷入早熟和局部最优的情况,本文从三个方面进行改进,提出基于随机过程的SPPSO.下面分别介绍三种改进策略,分别是采用随机变量作为学习因子、粒子陷入局部最优值时候的挣脱机制以及根据布朗运动的吸收与反射思想,提出粒子的越边界处理机制.
3.1 采用随机变量作为学习因子
本文认为,在搜索空间的粒子应当具有自己的认知和判断能力,有些粒子会对自身寻找到的最优位置的置信度高一些,有些粒子会更相信群体寻找到的最优位置,这就导致了不同粒子应该要有不同的学习因子c1和c2.在自然现象和社会现象中,大量随机变量都服从或者是近似服从高斯分布,鉴于此,本文采用高斯随机分布生成学习因子. c1和c2的确定方式描述如下:
Step 1:根据文献[12]将(c )2 的值取为1.494.
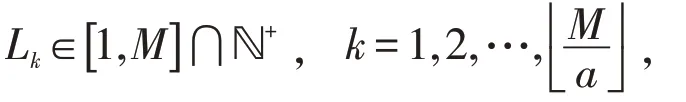
Step 3:将Step 2 生成的随机变量Lk作为粒子的位置索引,并定义第Lk个粒子的学习因子c1为服从区间[1,2.988]上均匀分布的随机变量,相对应的学习因子c2的值则为1.494×2-c1.
3.2 粒子陷入局部最优值时候的挣脱机制
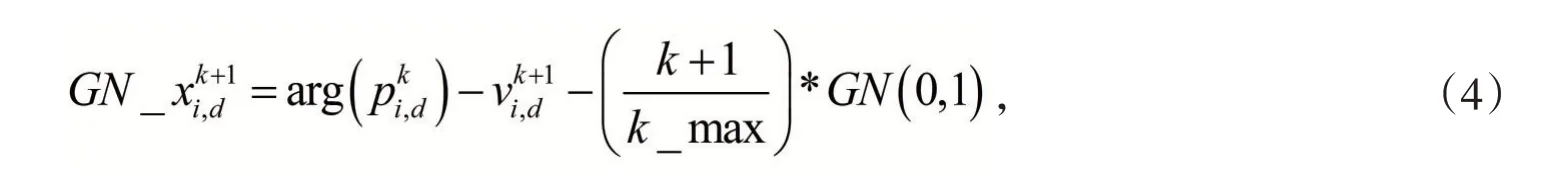

表1 6个测试函数的函数名、表达式、解空间以及目标值

目标值f4函数名Rosenbrock表达式f4( )n-1[ ]100( )xi+1-xi x =∑i=1 2+( )xi-12解空间[ ]-30,30 n f5 Ackley x2 i■ ■■■f5( )x =-20e■ ■■■-0.21 n∑i=1■ ■■n-e 1n∑i=1■ ■■cos 2πxi+20+e [ ]-32,32 f6 Griewank f6( )x =1 n ■xi nx2 4000∑i=1i -∏i=1■■ ■■■i+1[ ]-600,600 0 0 0
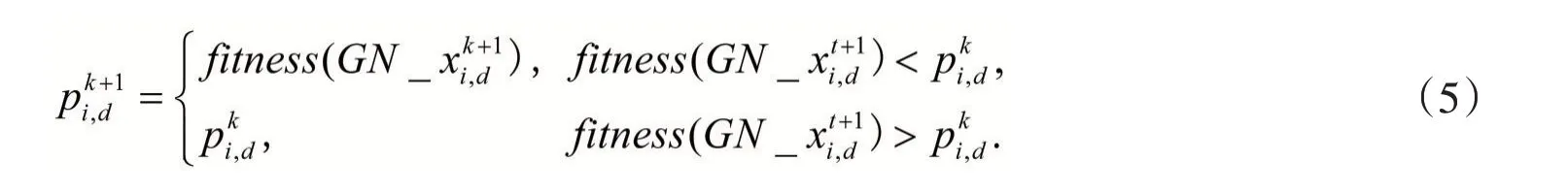
3.3 引入布朗运动的吸收与反射思想
粒子在解空间中搜索最优解时,常常会超出解空间的范围,从而导致算法不收敛或者是收敛不到目标值,为此,本文引入布朗运动的吸收与反射思想,定义描述[13]如下:
令{ X( t )}是布朗运动,回忆Tx是首次击中x 的时刻,定义Z( t )为:

其中式(6)表示在布朗运动击中x 时,就永远保持,式(7)表示在布朗运动到负半轴时,就以直线y=0 为对称轴,反射回正半轴.
式(6)和式(7)表明布朗运动在到达某个给定值后会被吸收且布朗运动不允许出现负值.本文借鉴这种思想,对要超过的粒子采取概率吸收或者映射的策略,防止粒子飞出解空间,具体公式描述如下:

其中bound_max,bound_min 分别为边界的最大最小值,a,r 为服从区间[0,1]上均匀分布的随机变量.
3.4 算法实现
本文算法的具体实现流程如下:
Step 1:初始化算法和参数;
Step 2:计算目标函数值;
Step 3:获取粒子局部极值和全局极值;
Step 4:检查局部极值是否有变化,有则转Step 5,反之则转Step 6;
Step 5:根据式(1)和式(2)更新粒子速度和位置;
Step 6:根据式(2)、式(3)、式(4)更新粒子速度、位置和局部极值;
Step 7:检查粒子是否越界,是则转Step 8,反之转Step 9;
Step 8:根据式(8)更新粒子位置;
Step 9:是否满足终止条件(达到最大迭代步数或者是满足终止精度),是则转Step 10,反之循环Step 2~Step 9;
Step 10:输出并保存结果,结束.
4 实验与结果分析
本文采用5个经典的基准函数外加一个测试函数进行仿真实验,并与标准粒子群算法、惯性权重线性递减的粒子群算法在寻优精度、收敛速度、寻优正确率等方面的性能进行比较.6个目标函数如表1所示,其中f1为文献[8]中标准粒子群算法的测试函数(该函数主要目的是为了凸显PSO算法的缺点,故函数值较其他有所不同), f2~f6为常用的标准测试函数[14-15].
本文在Intel(R)Core(TM)i7-8750H CPU@2.20GHZ 的处理器,16.00GB 的内存,windows 10系统的电脑环境下,利用python 3.7对每个函数进行20重复独立的次仿真实验并求平均值,分别对同一函数不同算法间收敛时所寻找到的最优目标值、迭代步数和正确率进行数据的对比并分析实验结果.
部分参数设置如下:最大迭代步数k_max=100,学习因子c1=c2=1.494,最大权重值w_max=0.9,最小权重值w_min=0.4(现有的文献介绍中,最值权重的设定往往是根据经验,其中标准粒子群的权重设置为1),函数维数dim=30,种群大小M=30.
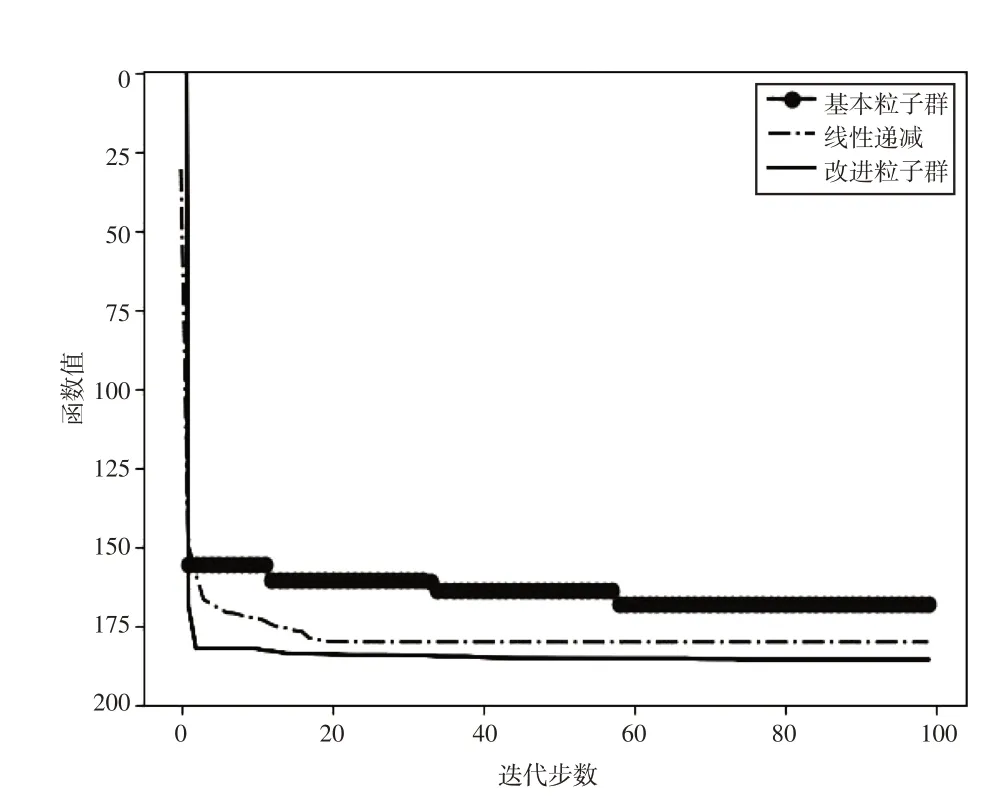
图1 测试函数寻优过程曲线图
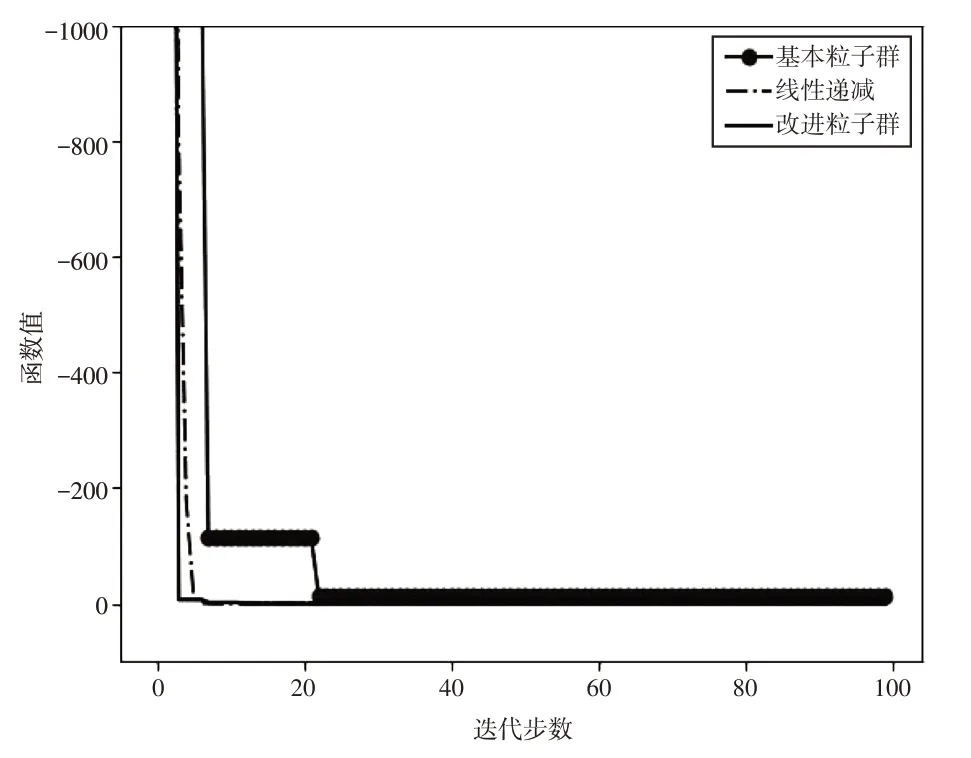
图2 Sphere函数寻优过程曲线图
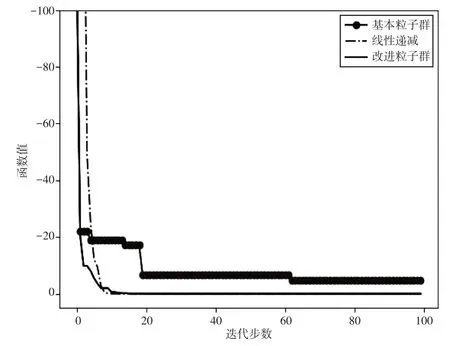
图3 Schwefel 2.22函数寻优过程曲线图
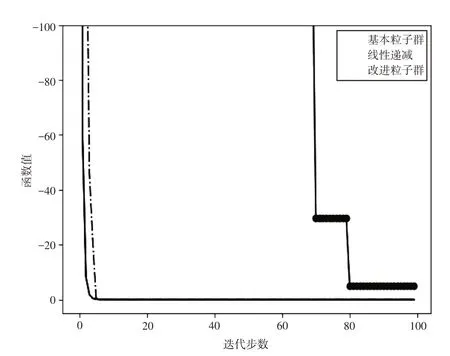
图4 Rosenbrock函数寻优过程曲线图
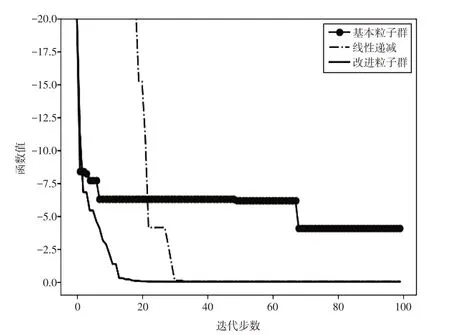
图5 Ackley函数寻优过程曲线图

图6 Griewank函数寻优过程曲线图
4.1 寻优过程可视化分析
图1~图6 是算法在寻优过程中,目标函数值随着迭代步数增加而变化的曲线图.该图表明,SPPSO算法在迭代过程中,收敛速度明显快于标准粒子群算法,较线性递减权重法也有一定的优势,特别是面对多峰函数的时候;寻优精度也明显高于标准粒子群算法,在测试函数的仿真实验中,SPPSO更是进一步体现了在寻优精度上的优势.
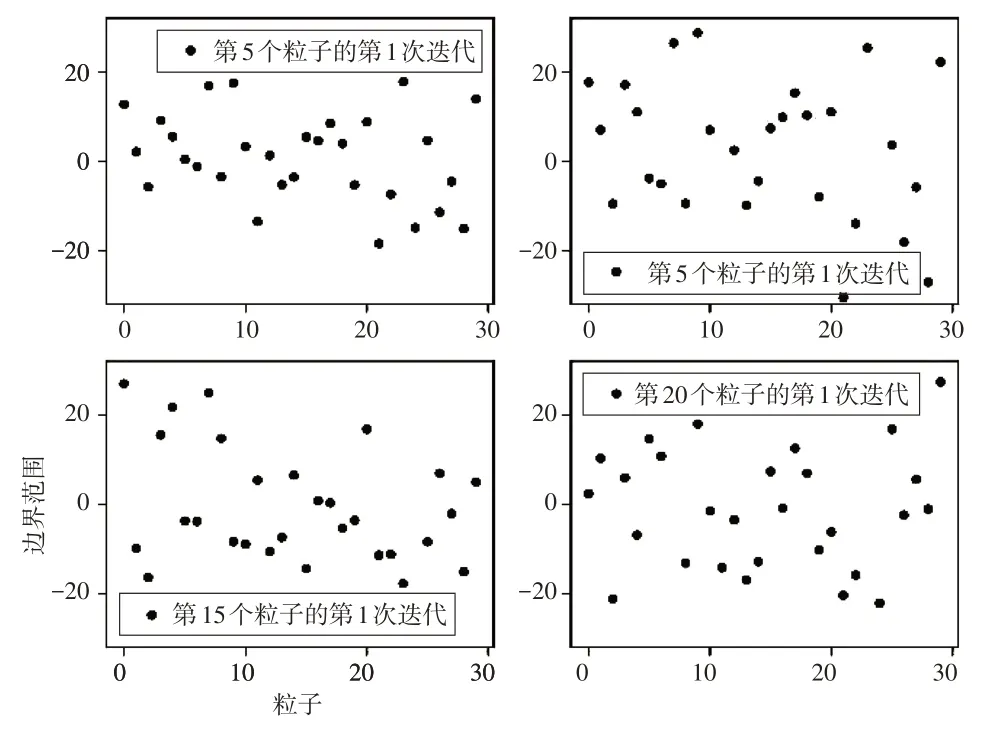
图7 第1次迭代粒子位置图
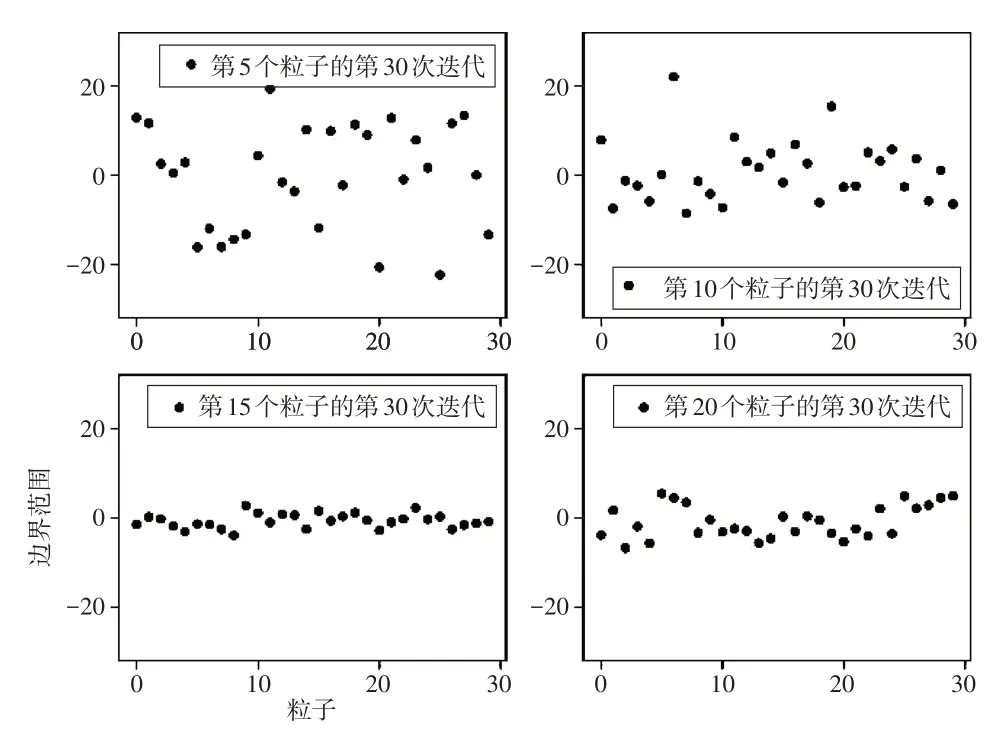
图8 第15次迭代粒子位置图

图9 第30次迭代粒子位置图
4.2 粒子位置分析
图7~9 是Ackley 函数(其他函数的实验图类似,这里不再赘述)在第5,10,15 以及20 个粒子第1,15,30次迭代时候的位置变化散点图.该散点图表明,在初始阶段,粒子几乎布满整个解空间,在寻优过程中,粒子位置不会超出解空间的边界范围.同时,体现了在寻优过程中粒子的位置从一开始散乱的分布在整个解空间(如图7所示),寻优过程中有向最优位置逼近的趋势(如图8所示),以及最后到达最优位置(如图9所示),这样的一个变化过程.
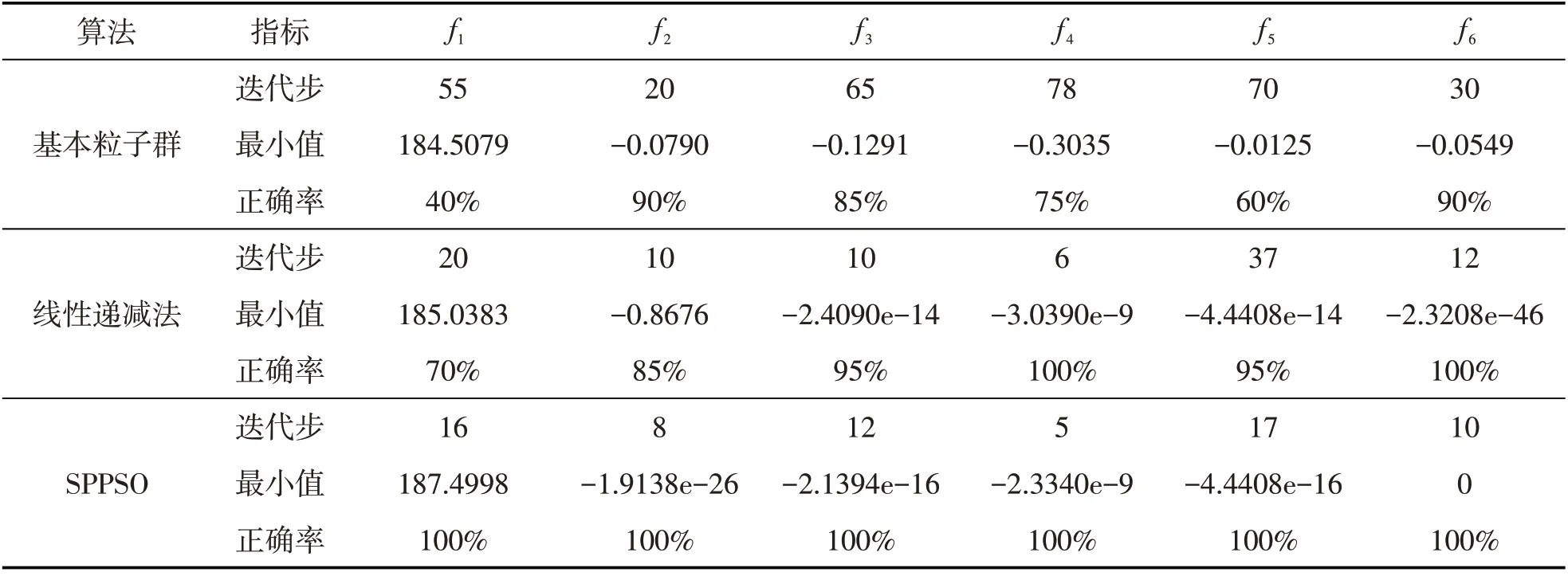
表2 6个测试函数收敛时的指标对比
4.3 结果分析
表2是仿真实验达所用的6个测试函数收敛时的指标对比表,该表表明基本粒子群算法收敛速度相较于其他两种算法就显得慢了许多,虽然线性递减法和SPPSO算法都能快速的收敛,但在面对多峰函数f5和f6时候,SPPSO算法体在收敛速度上较线性递减法会更胜一筹.而对于搜索到的平均最小值而言,基本粒子群相对其他两种算法来说,效果最差,误差也比较明显,线性递减法和SPPSO算法总体差异不是很大,但在精度上,SPPSO会较高一些,其中在测试函数f1中显得特别明显.同时,对于这6个测试函数的仿真实验,SPPSO算法总能收敛到目标值的误差许可范围内(允许误差为1e-6),而基本粒子群算法常常收敛到局部最优解,这进一步体现了SPPSO算法在面对陷入局部最优解时,挣脱机制的良好性能,当然,较线性递减法也有一定的优势.
5 结束语
本文从将随机变量作为学习因子、增加陷入局部最优时的挣脱机制以及增加粒子越边界处理机制这三个方面对基本粒子群进行改进,使得算法能够更快速准确地收敛到最优目标函数值.5个经典的基准函数和一个测试函数的仿真实验结果表明,SPPSO 算法相比PSO 算法和权重线性递减的PSO 算法,在寻优精度、收敛速度以及平均正确率上都有所改善,特别是面对多峰函数的时候,效果更加明显.此外,粒子群算法目前已应用于其他算法的优化,比如代替传统的梯度算法在支持向量机参数方面的优化.本文所提出算法是通过改进粒子群算法,并且优于后者,故而有着和粒子群算法同样的功能,且理论上效果更好.
