基于聚类的目标约简高维多目标差分进化算法
2020-06-28车旭,许峰
车 旭,许 峰
(安徽理工大学数学与大数据学院,安徽 淮南 232001)
现实中的最优化问题有时为多目标优化问题(Multi-objective Optimization Problem, MOP),甚至为高维多目标优化问题(Large-dimensional Multi-objective Optimization Problem, LMOP)。此类问题要求算法既能平衡多目标间的冲突,又要适应高维多目标中高维复杂空间的搜索需求,保证Pareto最优解集的收敛性和分布性。多目标进化算法(Multi-objective Evolutionary Algorithm, MOEA)是目前公认的求解MOP最有效的优化方法,但在求解LMOP时算法性能通常大幅下降,普遍存在计算复杂度高,近似解不能很好地逼近真实Pareto前沿,分布不均匀,稳定性差等问题。因此,如何针对高维多目标优化问题的特性,设计出高性能的MOEA以满足LMOP的求解需求已成为进化算法研究中的热点问题。
目前,一些性能较优的求解LMOP的MOEA已经陆续被提出,主要分为两类:一类是基于精英选择的高维多目标进化算法,代表性算法有NSGA-III、GrEA、SPEA2+SDE等,这类算法适合求解目标维数不太高但Pareto前沿较复杂的高维多目标优化问题;另一类是基于多目标分解的高维多目标进化算法,代表性算法有MOEA/D、Adaptive-MOEA/D、MOEA/D-AGR等,这类算法适合求解目标维数较高但Pareto前沿较简单的高维多目标优化问题。
2006年,Deb[1]和Brockhoff[2]分别从不同角度提出了在高维多目标进化算法中进行目标约简的思想;2015年,Bandyopadhyay[3]将目标约简思想应用于高维多目标差分进化算法;2016年,Blasco[4]在进行高维Pareto前沿分析时引入了相似距离,并将其用于目标约简;2018年,Monalisa[5]在一种多目标差分进化算法中引入聚类方法以进行目标约简。
本文在前人工作的基础上,将聚类方法加入一种基于精英保留策略的高维多目标差分进化算法,用以进行目标约简,利用DTLZ测试函数对新算法进行了数值实验和性能测试,并与其他算法进行了比较。
1 高维多目标差分进化算法
1.1 多目标差分进化算法
差分进化算法(Differential Evolution Algorithm, DE)是1995年Rainer Storn和Kenneth Price提出的一种基于进化思想和种群差异的群智能优化算法。DE算法的原理简单,受控参数少,全局收敛速度快。
多目标差分进化算法(Multi-objective Differential Evolution Algorithm, MODE)是在差分进化算法的基础上发展起来的一种多目标进化算法。本文采用的是基于精英保留的多目标差分进化算法,精英选择主要包含快速非支配排序、拥挤密度估计和精英个体保留3项操作,算法流程如图1所示。

图1 精英选择多目标差分进化算法流程图
1.2 高维多目标差分进化算法
通常目标维数超过4的多目标优化问题称为高维多目标优化问题。高维多目标优化算法求解性能不佳的主要原因是目标搜索空间和Pareto非支配解集均呈指数级增长,精英选择和解集的分布性不易实现,具体表现为:
1)Pareto最优前沿为超曲面,计算复杂度急剧增加,收敛速度大幅下降;
2)Pareto支配关系成立的概率大幅下降,支配个体出现的比例大幅增加,使得精英选择的压力急剧减弱,收敛精度大幅下降;
3)目标函数空间的数据具有稀疏性,各种基于距离的维护种群多样性的方法基本无效,使得解集的分布性大幅减弱。
为了提高高维多目标优化算法的性能,许多学者提出了多种有效的改进方法。这些改进方法主要分为下列三类:
1)提高高维多目标优化算法的收敛性能,关键技术包括:新型Pareto支配方法、非Pareto支配方法、精英选择策略等;
2)提高高维多目标优化算法解集分布性,关键技术包括:拥挤距离方法、网络策略、小生境技术等;
3)降低高维多目标优化算法的维数和复杂度,关键技术包括:多目标分解、冗余目标删除、偏好空间缩减等。
本文的算法主要涉及精英选择策略和目标约简。
1.3 多目标优化最优解集的评价标准
通常可以对多目标优化最优解集从解的收敛性和分布性两方面进行评价,常用的量化评价指标有:
1)收敛性指标γ
γ指标衡量非支配解集Q对理论Pareto最优解集P*的逼近程度,计算公式为
(1)
式中:di为非支配解集Q中的个体i与P*中距离最近个体的距离。显然,γ越小,表明算法取得的非支配解集Q逼近理论Pareto最优解集P*的程度越高,即算法的收敛性越好。
2)分布性指标Δ
Δ指标衡量非支配解集Q中个体的分布性和均匀性,计算公式为
(2)

2 基于聚类的多目标约简差分算法
2.1 聚类与目标约简
近年来陆续有学者从统计学角度出发,提出根据目标函数间的相关性进行目标函数的约简[6-7]。本文采用的相关性指标是相关距离,定义如下:
(3)
式中:A=(a1,a2,…,an)T,B=(b1,b2,…,bn)T是两个n维向量。上述定义实际上就是对统计学中的样本相关系数做了一个简单的变换,其目的是使得D(A,B)∈[0,2]。
根据相关距离利用聚类的方法进行目标约简的步骤如下:
1)对m个目标f1(x),f2(x),…,fm(x)和n个个体X1,X2,…,Xn,得到下列n×m矩阵
2)对上述矩阵,根据式(3)计算得到下列对称的相关距离矩阵如下
其中,D(fi,fj)为向量A=(fi(X1),fi(X2),…,
fi(Xn))T,B=(fj(X1),fj(X2),…,fj(Xn))T间的相关距离。
3)对相关距离矩阵,用K-均值聚类方法对其进行聚类,在同一聚类中,最终只保留聚类中心。这样做的目的是在若干相似的目标函数中只保留一个最具代表性的目标,其结果是既约简了目标函数的维数,又在很大程度上保留了冲突较大的目标函数,即确保了约简后的问题解的质量不会大幅下降。
2.2 算法流程
本文提出的基于聚类的目标约简高维多目标差分进化算法(Multi-objective Differential Evolution Algorithm using Clustering, MODEC)的流程如下:
1)种群初始化;
2) 根据2.1中的基于精英保留的多目标差分进化算法(MODE)对种群进行非支配排序、选择、交叉、变异、精英选择,得到新种群;
3) 根据式(3)计算得到目标函数的相关距离矩阵;
4) 对相关距离矩阵,用K-均值聚类方法对目标函数进行聚类,约简目标函数;
5) 对约简目标集用MODE算法进行新的进化,得到约简问题的Pareto最优解集;
6) 若满足终止条件,则算法终止;否则转2),对全目标集用MODE算法进行优化,直至满足终止条件。
算法之所以轮流在全目标集和约简目标集中搜索,主要目的是同时兼顾解集的质量和算法的运行效率。
3 数值实验与算法性能评测
为了评测MODEC算法的性能,选取4~20目标的标准测试函数集DTLZ1~4[8]进行数值实验。硬件配置为Intel Core I5 2.5GHz、4G内存,开发环境为Matlab2014。实验参数设置:变量维数为20,进化代数为1 000,种群规模为100,交叉概率为0.8。
图2~图9分别给出了DTLZ1~4的理论Pareto最优前沿和MODEC算法生成的Pareto最优前沿。其中,目标维数为10。

图2 DTLZ1理论Pareto最优前沿

图3 DTLZ1的MODEC算法Pareto最优前沿
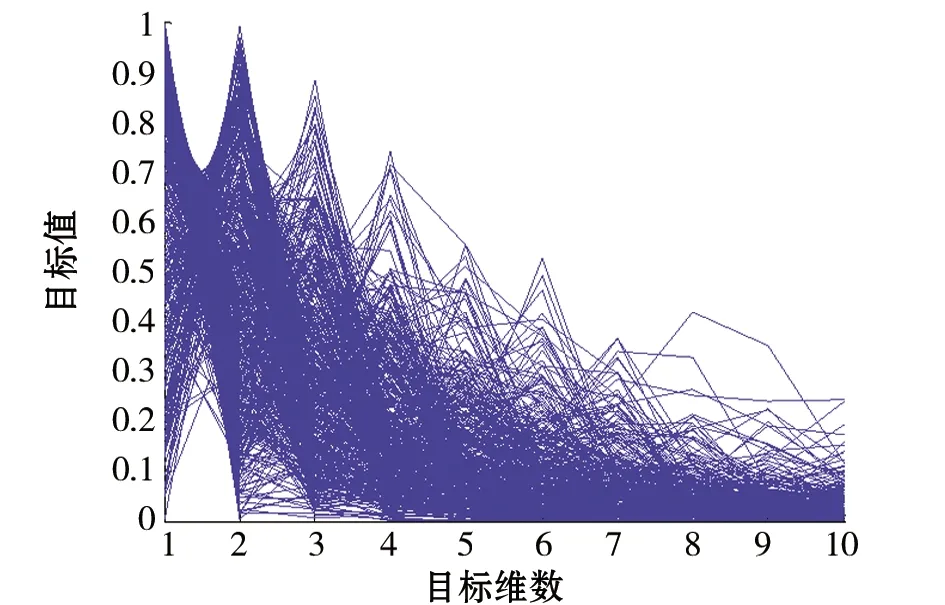
图4 DTLZ2理论Pareto最优前沿

图5 DTLZ2的MODEC算法Pareto最优前沿

图6 DTLZ3理论Pareto最优前沿

图7 DTLZ3的MODEC算法Pareto最优前沿
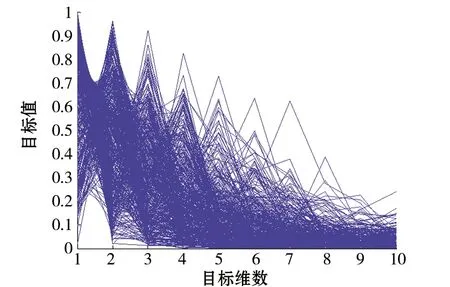
图8 DTLZ4理论Pareto最优前沿

图9 DTLZ4的MODEC算法Pareto最优前沿
从上述图形中可以直观地看出,MODEC算法不仅可以有效约简目标维数,而且约简后的问题的Pareto最优前沿较好地逼近了理论Pareto最优前沿。
为了进一步定量地评价MODEC算法的性能,本文将其与目前具有代表性的NSGA-III和MOGASd算法[9]581对DTLZ1~4的优化情况进行了比较,评价标准采用通用的γ指标和Δ指标。对比实验中的参数均采用相应文献中的推荐值,γ指标和Δ指标为各算法独立运行10次的平均值,具体结果见表1。

表1 三种算法的γ和Δ指标对比
表1中的γ指标和Δ指标显示,MODEC算法在解集的收敛性和分布性两方面均明显优于NSGA-III,其原因在于NSGA-III仅仅是在NSGA-II基础上改进而得,对高维问题的优化效果欠佳。与MOGASd算法相比,MODEC算法解集的收敛性略占优,而在分布性方面则基本相当,其原因是MOGASd算法采用了适应值共享方法以维持种群多样性[9]590。
4 结论
数值仿真实验和统计指标表明,本文提出的基于聚类的目标约简高维多目标差分进化算法具有较好的收敛性和分布性,可有效地求解高维多目标优化问题。需要指出的是,与其他群智能优化算法类似,高维多目标差分进化算法也存在着诸多不足,如控制参数难以确定、搜索有一定的盲目性、后期收敛速度慢、易陷于局部最优等。并且,差分进化算法的理论基础还比较薄弱,对算法性能的研究只能圄于对测试函数的对比实验,这在一定程度上阻碍了差分进化算法的研究与应用。
