悬索桥主缆与鞍座抗滑移安全参数的合理设定研究

黄钰程，魏旭阳，王越，许增锋，石多福

（1.兰州交通大学，兰州730070；2.陕西工业职业技术学院，陕西 咸阳712000；3.浙江奥普有限公司，杭州310011；4.南京艺融园林工程有限公司，南京210000；5.日喀则公路分局日喀则公司，西藏 日喀则857000)

1 引言

经研究表明，悬索桥主缆和鞍座之间的抗滑移能力是保证其结构安全的决定性因素之一，通过设置参数，调节摩擦力大小，如果抗滑移能力在安全范围之内，则产生的摩擦力可以有效阻止滑移，起到安全保护作用，反之，将对悬索桥结构安全造成威胁【1】。然而，当前在主缆与鞍座抗滑移安全系数方面的研究较少，很多问题缺乏实践论证，本文将从相互作用力角度出发，合理设定安全参数。

2 悬索桥主缆与鞍座抗滑移安全参数设定研究的必要性

2.1 设定方法

依据悬索桥设计相关要求，主缆与鞍座抗滑移关系如下：

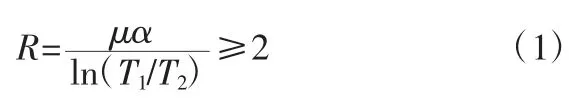
式中，R为主缆与鞍座抗滑移系数；α 为位于鞍槽上主缆包角；T1和T2分别为位于鞍座两侧主缆紧边拉力和主缆松边拉力；μ 为隔板与槽底之间的摩擦因素，取值0.15。

为了保证悬索桥结构安全，必须满足公式（1）中各项参数之间的关系，将0.15 作为摩擦因数下限。经过转换处理得到公式（2）：

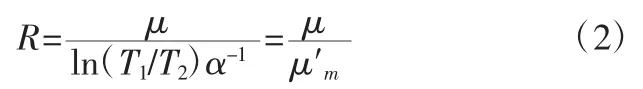
2.2 存在的问题

式（2）的建立出于计算简便，容易理解分析，但是，安全系数估计过于保守。如果用摩擦参数μ 来代替参数μ′m，则鞍座受横向和侧壁摩擦力的计算精度偏低。另外，此公式的物理意义不清晰作为安全系数，从参数性质来看，均为摩擦因数，但是，因含义不同，导致比值含糊不清。在计算实际抗滑移安全性时，依据鞍座结构与摩擦抗力之间的关系，很难准确度量安全性大小。当隔板与槽底摩擦因数相同，且鞍座结构参数存在差异时，经过计算得到的实际抗滑移安全系数和摩擦抗力数值不同【2】。因此，利用式（2）无法保证抗滑移安全准确性。除此之外，式（2）适用受限，如果抗滑移经过改良处理，则无法利用此公式求解参数。由此可以推算，虽然式（2）可以用来探究抗摩擦安全性问题，但是，在计算精度和应用范围等方面存在较大问题。

2.3 问题探究必要性

悬索桥主缆和鞍座之间抗滑移的计算是提升抗滑移能力的前提，而摩擦力参数的调节与确定是控制主缆与鞍座滑移的主要途径【3】。当前构建的抗滑移模型过于简单，在问题分析方面存在疏漏【4】。为了确保公路大桥等工程的安全，对主缆和鞍座之间抗滑移问题展开研究具有一定必要性。

3 主缆与鞍座摩擦抗力力学分析

依据鞍座内部结构，沿着垂直方向在其槽内配置摩擦板，产生抗力，以此防止鞍座和主缆之间产生滑移。其抗力计算公式为：

式中，Fk为鞍座与主缆间的摩擦抗力；FB1为槽底接触面产生的摩擦抗力；FH2为侧壁接触面产生的摩擦抗力；FH3为垂直方向接触面产生的摩擦抗力。

假设选取沿着垂直方向布设摩擦板作为力学分析对象，探究摩擦抗力问题。将相邻隔板、承揽槽侧壁与边隔板间看作子鞍座，记录子鞍座的数量为n+1。如果子鞍座的编号为i，则产生的摩擦抗力计算公式为：

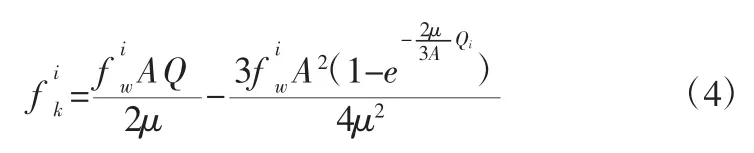
式中，为编号为i的子鞍座在其内部结构中产生的侧壁压力；A为鞍座列索股长度；Q为鞍座列索股高度；Qi为编号为i的子鞍座列索股高度大小为编号为i的子鞍座对应的列索股体积力，计算公式如下：

式中，mbi为编号为i的子鞍座对应的列索股数量；Fb表示不同列索股数对应的荷载大小；P为鞍座承受的总荷载设计值。

依据上述关系模型，可以将侧壁接触面和竖向接触面产生的摩擦抗力总和的计算结果用以下公式来求取：

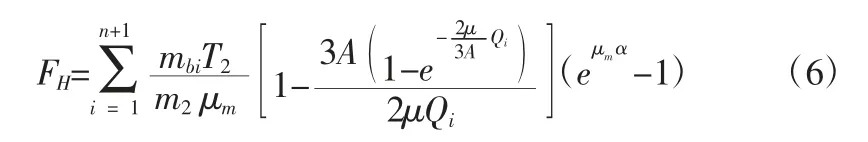
式中，T2为松边拉力；μm为摩擦因数。

在式（6）基础上，采取纵向积分计算，可以获取槽底间摩擦抗力计算公式：

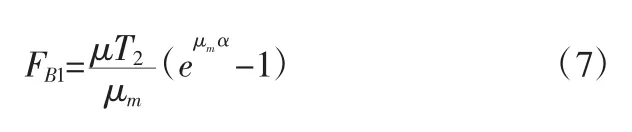
对式（6）和式（7）进行合并与简化处理，得到Fk计算公式：

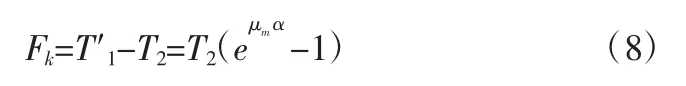
式中，T′1为α 截面处的拉力。

4 抗滑移安全参数的合理设定

4.1 安全参数的定义

基于上述推理分析，针对悬索桥结构抗滑移安全参数的设定，以松边拉力和紧边拉力视为固定不变值，确定各项参数【5】。在式（2）基础上进行修正，得到实际摩擦因数，将实际摩擦数值与假设摩擦数值之比记为安全系数，则经过修正处理后的安全系数UP1计算公式如下：

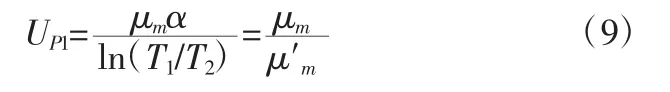
式（6）虽然较式（2）计算精准度高一些，但只能表现出鞍座抗滑移部分性能，且无法直接获取信息。为了使得抗滑移问题更加清晰，本文从结构抗力角度出发，对式（9）进行进一步改进，以实际摩擦抗力与需求抗力之间的比值作为安全系数，计算公式如下：

依据式（8），对式（10）进行转换可得：

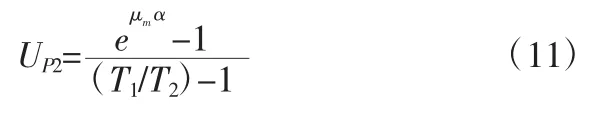
由式（9）和式（11），可以得到悬索桥摩擦抗力安全系数之间的关系：

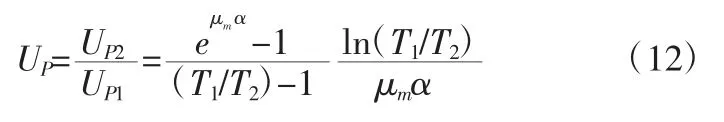
同样，以武汉鹦鹉洲长江公路大桥项目为例，对摩擦抗力安全系数进行对比分析，通过收集相关数据，将其代入公式中，计算结果如下：

抗滑移安全系数UP为4.32 时，计算结果为110%，UP2为6.07 时，计算结果为194%，UP1为5.28 时，计算结果为157%。

依据计算结果可知，经过处理后的安全系数计算结果超出式（2）计算结果幅度较大，UP2对应的安全系数更高一些，且式（11）可以直接描述抗力变化情况，便于工程推行过程中抗力滑移问题的直接挖掘。因此，本文建议选取式（11）来计算抗滑移安全系数。

4.2 抗滑移安全参数实验分析及设定

为了深入探究抗滑移安全参数，本文采用实验分析法，依据前文介绍各参数之间的关系，选取单个索股高度、索股宽度、鞍座包角、中列索股比重、松边拉力、紧边拉力作为参数指标，分别用Q/mb、A、α、mb/ms、T2、T1表示，对2 个抗滑移安全系数进行对比分析，通过对比分析实验数值，从而深入分析抗滑移安全系数关系，提出更加详细的设定方案。

4.2.1mb/ms变化情况下的抗滑移安全系数统计结果分析

当中列索股比重mb/ms逐渐增加时，安全系数均有所增加，且均呈正比例关系提升数值。其中，UP2抗滑移安全能力更高一些，当mb/ms数值大于0.14 时，UP2数值最大，其取值体现出价值。

4.2.2 α 变化情况下的抗滑移安全系数统计结果分析

当中鞍座包角α 逐渐增加时，安全系数随之增加，UP2抗滑移安全能力更高一些，当α＞0.88 时，UP2大于其原始值和UP1变化值，体现参数价值。

4.2.3A变化情况下的抗滑移安全系数统计结果分析

当索股宽度A逐渐增加时，安全系数随之减小，当A增加到0.08 时，UP2变化值仍然具有优势，而后随着宽度的增加逐渐减小，低于原值，不再具有安全优势。

4.2.4Q/mb变化情况下的抗滑移安全系数统计结果分析

当单个索股高度Q/mb逐渐增加时，安全系数随之增加，UP2抗滑移安全能力更高一些，当Q/mb＞0.07 时，UP2开始体现优势。

综上分析，为了提高抗滑移安全系数，可以设定参数如下：mb/ms＞0.14、α＞0.88、A＜0.08、Q/mb＞0.07。同时满足上述关系时，能够在一定程度上提高安全系数，使其满足抗滑移安全需求。

5 结语

本文围绕悬索桥主缆与鞍座安全问题展开研究，选取安全参数作为研究对象，通过理论分析，掌握各参数之间的关系，采用实验分析方式，分别探究各参数发生改变时对应的安全系数变化情况，依据实验结果，给予安全参数设定方案。通过本文的研究，为悬索桥安全设计提供了参考依据。