一类比估计量在数量特征敏感问题调查方法中的应用
2020-06-24李珊珊
李珊珊,刘 迪
(河套学院理学系,015000,内蒙古,巴彦淖尔)
0 引言
数量特征敏感问题调查方法的主要目的是估计敏感变量的均值或总值,例如调查员工平均额外收入多少,企业偷税金额,学生作弊次数等。1969年Greenberg[1]提出了调查数量特征敏感问题的随机化回答方法,Himmelfarb和Edgell[2]设计了加法模型,许多学者在一些经典模型的基础上进行了研究,文献[3]设计了一种数量特征敏感问题的改进模型;文献[4]以Greenberg模型与加法模型为基础提出了新模型,减少估计量的方差,提高了估计精度;文献[5]在2种经典模型的基础上给出了3种数量特征随机化回答模型。金莹[6]对2种经典模型作了改进,提出一种改进的Greenberg模型,提高了估计精度。
在直接调查中,通常利用与调查变量相关的辅助变量,借助辅助信息来提高估计敏感变量的精度。文献[7]在2006年结合比估计提高了Warner模型的效率;文献[8]在2007年使用了回归分析提高了一般化随机装置的效率;文献[9]提出双辅助信息敏感性问题问卷调查技术;文献[10]利用辅助信息提高属性特征随机化回答技术的效率。本文探讨基于金莹提出的改进的Greenberg模型,构造一类比估计量提高估计精度的问题。一类比估计量由Naik and Gupta[11]提出,包括均值、比估计、乘积估计、Srivastava(1967) 、Walsh(1970) 、Reddy(1973、1974)、Sahai(1979) 、Vos(1980) 、Adhvaryu和Gupta[12-19]提出的估计方法。通过理论推导和数值比较,在一定的条件下,提出的估计量提高了估计效率。
1 金莹改进的Greenberg模型
金莹[6]提出改进的Greenberg模型调查方法。
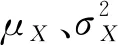
第2步:产生0-1分布的随机数di,且P(di=1)=p。

敏感性变量Y均值μY的估计量为
估计量的方差为
童话是属于儿童文学范畴的一种特殊的文字表现形式,是为了适应小学生心理发展特点而构建的一个虚拟世界,伴随在每位儿童的成长过程中。在实际教学中,为最大程度地发挥出童话的文学优势,激发学生的学习热情,保证童话课堂教学的有效性,教师可采用设置教学情境、拓展教学内容、组织课外活动等多种形式的教学方法,发挥童话的审美功能,进而激活学生的想象,丰富他们的情感体验,带领他们真正走进童话的世界。下面我就小学语文童话教学的三种策略展开探究。
2 改进的估计量
提出一类比估计量,用于改进的Greenberg模型。随机化装置盒中有外形相同的两类卡片:1)敏感变量值Y,辅助变量值T;2)无关变量值X,辅助变量值T。
然后将卡片1)、2)以预定的比例p和1-p放入一个盒子中,回答者有放回地从盒中抽取卡片,并作出真实回答:(z1,t1),(z2,t2),…,(zn,tn)。
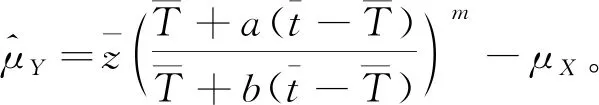
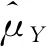
(1)

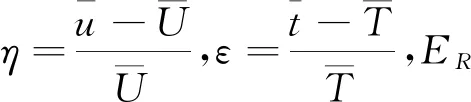
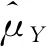
(2)

下面计算
综上
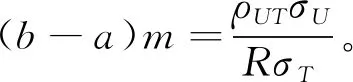
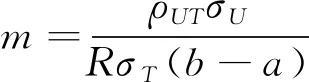
3 效率比较
3.1 比较估计量的偏差的大小

3.2 比较估计量的均方误差的大小
当a,b,m取一些值时得到一些重要的估计,如表1所示。
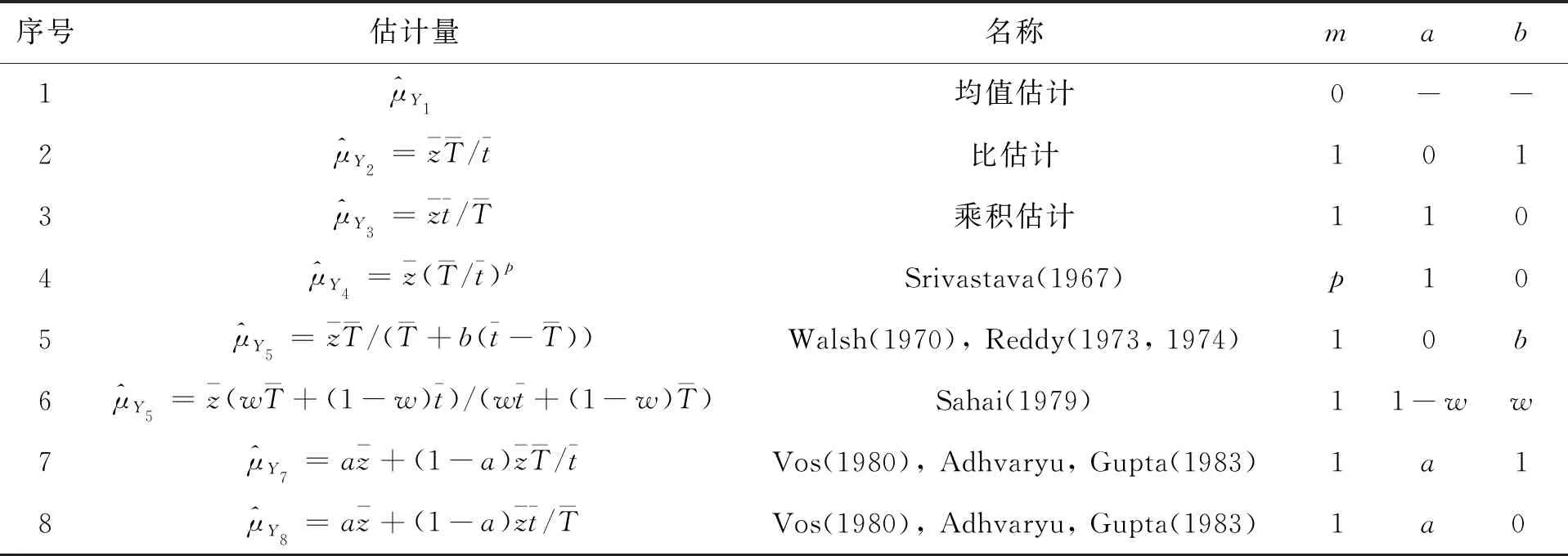
表1 提出的一类估计包括的估计量
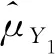
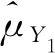
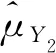
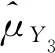
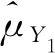
综上可以得出如下结论。
1)当K≤-1时,2K+1<(b-a)m<-1。
2)当-1 3)当-1/2 4)当0 5)当1/2 6)当K≥1时,1<(b-a)m<2K-1。 通过以上结论,可以在实验中根据不同值选择不同的参数范围。 K^μY1^μY2^μY3^μY4^μY5^μY6^μY7^μY81)0.340.531.705.820.190.190.190.198.882)-0.400.535.855.030.540.540.540.544.873)-0.140.212.011.200.180.180.180.180.904)0.240.632.056.540.280.280.280.289.77 从数值比较结果可以得出结论:利用辅助变量提出一类估计量的均方误差在参数一定的条件下优于金莹模型的效率,一类估计量中在参数不同的条件下包括7种不同的估计量,估计量的精度有所不同,再利用第3部分理论推导的结论,参数满足(b-a)m=ρUTσU/RσT可以得到最优的估计效率,从表2中可以大致看出模型在参数满足等式时的估计效率大致相同,而模型2)的效率较低的原因是因为选择的辅助变量与敏感变量的相关系数为0.02,这也从侧面验证了选择与调查变量无关的辅助变量时,不会提高估计效率。4 数值模拟
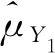


5 结论
