数学问题解答

2020年4月号问题解答

(解答由问题提供人给出)

(1)

当且仅当△ABC为等边三角形时式中等号成立.

(河南质量工程职业学院 李永利 467000)

证明令x=b+c-a,y=c+a-b,z=a+b-c，则x,y,z>0，且半周长

所以

于是(1)式等价于

⟺(xy+yz+zx)2≥3xyz(x+y+z)

⟺(xy)2+(yz)2+(zx)2+2xyz(x+y+z)

≥3xyz(x+y+z)

⟺(xy)2+(yz)2+(zx)2≥xyz(x+y+z)

(2)

而

(xy)2+(yz)2+(zx)2≥xy·yz+yz·zx

+zx·xy=xyz(x+y+z)，

即(2)式成立，从而(1)式成立.

由以上证明过程可知，当且仅当x=y=z即a=b=c亦即△ABC为等边三角形时(1)式中等号成立.

2537若抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交，探讨以下问题：

(Ⅰ)求过交点的直线围成的封闭图形的面积公式S,

(Ⅱ)求面积公式S的最值，

(Ⅲ)如图1, 当四边形ABCD的面积取最大值时，求四边形ABCD对角线AC、BD交点P的坐标，并且探讨其几何性.

(安康学院数学系 赵临龙 725000)

图1

图2

图3

解(Ⅰ)先来讨论2条二次曲线构成的图形面积.

由抛物线E方程与圆M方程，

得x2-7x+16-r2=0， (1)

则抛物线E与圆M相交的充要条件是

(a)若圆M经过坐标原点，则r=4，

此时，若圆M与抛物线E再相切2点C、D，则

但圆半径值矛盾.即圆M与抛物线E，不可能出现相切3个点情况.

此时，圆M过坐标原点，并且与抛物线E相交两点C、D，则四边形ABCD的点A、B与坐标原点O重合，四边形ABCD退化为三角形△OCD.

如图2，对于r=4,

由方程x2-7x+16-r2=x2-7x=0，

于是，当r=4(x=0)时，

三角形△OCD的面积S是

(b)如图1，由方程(1)知，

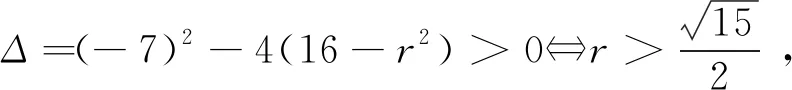
圆M与抛物线E有4个相交点A、B、C、D.

由于抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)都是关于x轴的对称图形，因此四边形ABCD是关于x轴对称的等腰梯形.

现设E与M的四个交点的坐标分别为

四边形ABCD面积为

(2)

于是，当且仅当14-4x=7+2x，

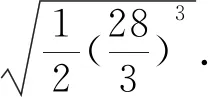
(c)如图3.由方程(1)知，

圆M与抛物线E有2个切点C、D.

此时，直线AB与直线CD重合，

四边形ABCD面积S=0.

现在考虑四边形ABCD面积S公式(2)：

同理，当r=4，则x=0，

即四边形面积公式(2)，包括了图2和图3的2种特殊情况.

即得到抛物线E与圆M交点的直线围成的封闭图形的面积公式S:

此时，三角形△OCD的面积S0是

(Ⅲ)由于四边形ABCD面积取最大值时，

若记AB、CD分别交x轴于点R、S，

则线段OP是线段OR、OS的几何平均

(河南省方城县教研室 邵明宪473200)

解由题意，

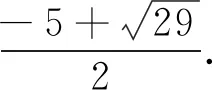
2539已知⊙O1，⊙O2相交于P，Q两点，过点P的割线段AB交⊙O1于点A，交⊙O2于点B.两圆在A，B处的切线交于点S，直线SQ交△O1O2Q的外接圆于另一点T.

求证：△O1O2P的外接圆直径等于线段ST.

(江西省高安市石脑二中 王典辉 330818)

证明设直线AO1与直线BO2交于点C.

因为SA切于⊙O1于点A，SB切⊙O2于点B，

所以有∠SAC=∠SBC=90°，

则知S，A，C，B四点共圆.

连接AQ,BQ,PQ,

有∠PQA=∠PAS，∠PQB=∠PBS，

而∠PQA+∠PQB+∠PAQ+∠PBQ

=∠AQB+∠PAQ+∠PBQ=180°，

所以∠PAS+∠PBS+∠PAQ+∠PBQ

=∠SAQ+∠SBQ=180°.

有S，A，Q，B四点共圆.

又因为∠AQB+∠ASB=180°，

∠ACB+∠ASB=180°，

有∠AQB=∠ACB，

所以A，C，Q，B四点共圆.

故知S，A，C，Q，B五点共圆.

延长QO1与⊙O1交于点A1，

延长QO2与⊙O2交于点B1.

设⊙O1在点A1的切线与⊙O2在点B1的切线交于点S1.

有S1，A1，Q，B1四点共圆.

连接PA1，PB1，

于是∠A1PQ=∠B1PQ=90°.

可知A1，P，B1三点共线.

因为∠PAQ=∠PA1Q，∠PBQ=∠PB1Q，

所以在△AQB和△A1QB1中，

有∠AQB=∠A1QB1.

又因为S，A，Q，B，与S1，A1，Q，B1分别四点共圆，

所以∠AQB+∠ASB=∠A1QB1+∠A1S1B1

=180°，

故有∠ASB=∠A1S1B1.

而S1，A1，Q，B1和S，A，C，B分别四点共圆，

则有∠A1S1B1+∠A1QB1=∠ASB+∠ACB

=180°，

所以∠A1QB1=∠ACB.

由此可知∠O1CO2=∠O1QO2.

于是，知点C在△O1O2Q的外接圆上.

由上述证明的S，A，C，Q，B五点共圆，

知∠TQC=∠SBC=90°.

即CT为△O1O2Q的外接圆直径.

有TO1⊥AC，而AS⊥AC，所以AS∥TO1.

设直线AC交直线SQ于D，

易证△DQO1∽△DCT，

①

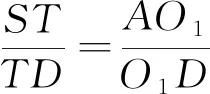
②

有ST=TC，

所以△O1O2Q外接圆的直径等于ST.

由于△PO1O2和△QO1O2是关于O1O2为对称轴的对称图形，

所以△PO1O2≌△QO1O2，

即△PO1O2的外接圆直径等于ST.

2540设x,y,z是正实数，则

(1)

其中∑表示三元循环和

(四川成都金牛西林巷18号晨曦数学工作室 宿晓阳 610031)

证明由柯西不等式，有

(2)

由(2)式知欲证(1)式，即证

(3)

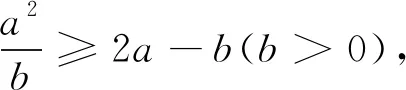
由上述不等式知欲证(3)式，即证

(4)

事实上，(4)式等价于

⟺4∑x3-2∑yz(y+z)

⟺4∑x3-2∑x2(y+z)

⟺2∑x2(2x-y-z)

⟺2∑x2[(x-y)+(x-z)]

⟺2∑(y+z)(y-z)2

此不等式显然成立，即(4)式成立，于是(1)式得证.

2020年5月号问题

(来稿请注明出处——编者)

2541设正实数a,b,c满足a2+b2+c2+abc≤4,x,y,z为任意实数，求证：

ayz+bzx+cxy≤x2+y2+z2.

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000)

(北京市朝阳区教育研究中心 蒋晓东 100028；北京市朝阳区芳草地国际学校富力分校 郭文征 100121)

2543在△ABC中，sinA=cosB=cotC，求C的值．

(浙江省海盐县元济高级中学张艳宗314300；北京航空航天大学图书馆 宋庆 100191)

(河南辉县一中 贺基军 453600)

2545如图1，△ABC中，E是BC边的中点，D是线段BE上一点(端点除外)， 设I1，I2分别为△ABD，△ACD的内心，则∠I1EI2=90°的充要条件是AB=AC．

(湖北省公安县第一中学 杨先义 434300)