点几何理论与GeoGebra实践①
2020-06-23张志勇罗建宇
张志勇 罗建宇
(1.江苏省常州市第五中学213001;江苏省张家港市沙洲中学215600)
我们知道,解析几何是用代数方法研究几何问题,思路清晰有章可循,但代数方法在计算过程中很难看出几何意义,于是为寻求能够更直接处理几何问题的代数方法,数学家们开辟了“几何代数”领域.张景中先生等建构的“点几何”理论,用简明的概念、平常的符号和代数运算的形式描述几何对象之间的关系,不仅符合数学直观,也能更方便地表达基本几何事实,而且有助于几何推理的简捷化[1][2].GeoGebra作为一款“专为教与学的动态数学软件”,内嵌有计算代数系统和指令输入方式,可对几何对象进行直接代数化处理,从而实现“形”(几何Geometry)与“数”(代数Algebra)的完美融合.巧合的是,GeoGebra的很多指令规则与点几何理论完全一致,可以说GeoGebra就是点几何理论的一个实践场.应用点几何理论于GeoGebra实践中,既是对理论的支持验证,也有助于软件的理解把握.
1 点的线性运算
点几何中定义了“点加点”和“数乘点”,即A+B=(xA+xB,yA+yB)、λA=(λxA,λyA);以此为基础,推导出两点线性组合uA+vB=tP的意义和uA+vB=rC+sD的表示,特别地,直线上任意一点都可以表示成P=tA+(1-t)B,△ABC平面上任意点P=xA+yB+(1-x-y)C.
GeoGebra支持点的线性运算.如图1,在指令输入框中输入“A+B”、“-2A”,得到D、E两点;输入“(A+B)/2”、“(A+B+C)/3”,得到线段AB的中点F和三角形ABC的重心G;输入“B-A+C”,可构造平行四边形ABHC的第四个顶点H.值得说明的是,GeoGebra有很好的帮助功能,如查看代数区中的坐标,可以发现D=(xA+xB,yA+yB)、E=(-2xA,-2yA);而图1右侧的作图过程,可查看每一个点的属性;另外A、B、C为给定的初始点.

图1
扩展开去,可通过语句“P=x*A+y*B+(1-x-y)*C”的输入,来构造△ABC平面上任意一点P;而有了任意点P后,又可在运算区中通过指令“Solve(P=x*A+y*B+(1-x-y)*C)”来获取参数x、y的值.

◆1、在绘图区中构造三点A、B、C和三角形t1;在运算区储存格1~4的指令域中分别输入“λ:=0.5”、“μ:=0.4”、“D:=λ*C+(1-λ)*A”、“E:=μ*B+(1-μ)*A”,得到AB、AC上两点D、E.
◆2、在绘图区中构造线段BD、CE和交点F;在运算区储存格5~7的指令域中,分别输入“Solve(F=x*B+(1-x)*D)”、“Solve(F=x*C+(1-x)*E)”、“Solve(F=m*A+n*B+(1-m-n)*C)”.


图2
说明:借助指令“AffineRatio()”,得到的只是系数的近似数;而在运算区应用“Solve()”求解方程时,可得到精确解.
以上实验结果可用点几何法证明如下(取A为原点):
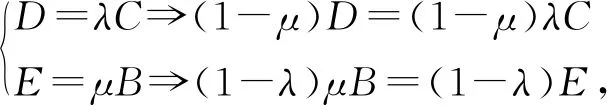
得(1-μ)D+(1-λ)μB=(1-λ)E+(1-μ)λC,
又(1-μ)+(1-λ)μ=(1-λ)+(1-μ)λ,
故而(1-μ)D+(1-λ)μB=(1-λ)E+(1-μ)λC
=(1-λμ)F,


2 点的数量积运算



图3
例2如图4,△ABC中,AB=AC,D是AB的中点,O是△ABC的外心,E是△ACD的重心.求证:OE⊥CD.
◆3、构造任意两点A、B和角度滑动条α,输入“C=e^(l*α)*(B-A)+A”得到C点;输入“Polygon(C,A,B)”,构造等腰三角形t1;输入(A+B)/2,得到AB边上的中点D.
◆4、输入“TriangleCenter(A,B,C,3)”,得到△ABC的外心O;输入“(A+C+D)/3”,得到△ACD的重心E;输入“(E-O)*(D-C)”,得到数量积d(如图4,结果为0,说明OE⊥CD).

图4
下面给出点几何法证明(取O为原点):
O是△ABC的外心⟹A2=B2=C2,
AB=AC⟹(B-A)2=(C-A)2
⟹B·A=C·A,
E是△ACD的重心

=0.
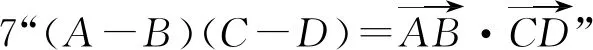
3 点的外积运算
点几何中将两点A、B的外积定义为AB=B-A,并且给出了三点A、B、C外积的概念,即ABC=xAyB+xByC+xCyA-xAyC-xByA-xCyB,表示△ABC的带号面积(A、B、C顺序为逆时针时ABC>0,顺时针时ABC<0).
GeoGebra中并没有两点外积、三点外积的定义,但指令“Cross(

◆5、构造三点A、B、C,输入“Polygon(A,B,C)”,得到三角形t1;输入“(A-B)⊗(B-C)”(或者“Cross(A-B,B-C)”,得到外积计算结果d.
说明:由图5的计算结果发现,外积的计算结果为三角形面积的2倍.事实上,由外积公式(a1,a2)⊗(b1,b2)=a1b2-a2b1,得(A-B)⊗(B-C)=(xA-xB,yA-yB)⊗(xB-xC,yB-yC),化简得到(A-B)⊗(B-C)=xAyB+xByC+xCyA-xAyC-xByA-xCyB,这一结果与点几何中的三点外积ABC的定义一致.也就是说,点几何中的ABC实际上表示的是△ABC带号面积的2倍(对应着平行四边形的面积).
◆6、构造滑动条t,分别输入“t*C+(1-t)*B”、“t*A+(1-t)*C”、“t*B+(1-t)*A”,得到点D、E、F;构造线段AD、BE、CF及相应的交点P、Q、R.


图5
以上结论用点几何法解答如下:
取C为原点,则
D=(1-t)B,E=tA⟹
(1-t)D+t2A=tE+(1-t)2B=(t2-t+1)P,
又BD=tBC⟹D=(1-t)B+tC,
所以有(t2-t+1)P=t2A+(1-t)2B+t(1-t)C;
同理(t2-t+1)Q=t2B+(1-t)2C+t(1-t)A,
(t2-t+1)R=t2C+(1-t)2A+t(1-t)B,
将三式作外积并略去零值项,得
(t2-t+1)3PQR=t6ABC+(1-t)6BCA+
t3(1-t)3CAB+t3(1-t)3ACB+
t3(1-t)3BAC+t3(1-t)3CBA,
因为ABC=BCA=CAB=-ACB
=-BAC=-CBA,



4 点的复数乘法
点几何中定义复数乘点为iA=i(x,y)=(-y,x),表示将点A(x,y)逆时针旋转90°得到点(-y,x);进一步的,取复数α=u+vi,有αA=uA+v(iA)=(ux-vy,uy+vx),如果用三角形式α=r(cosθ+icosθ)来表示的话,则αA的几何意义为将点rA逆时针旋转θ角得到点αA;进一步地,引进指数式eiθ=cosθ+isinθ,则有eiθA=(xcosθ-ysinθ,ycosθ-xsinθ).
在取定坐标系的情况下,GeoGebra中默认代数区为一复平面,因此点与复数是一一对应的,如在指令栏键入复数“P=3+4i”,在绘图区中构造点P(3,4),同时在代数区中显示复数“P=3+4i”.我们可以通过“属性对话框→代数区→坐标”的设置来实现点与复数的转换:将复数的坐标属性改为“直角坐标”,则复数切换为点;反之,将点的坐标属性改为“复数”,则点又可切换为复数(当然更改只是GeoGebra在代数区中的显示形式,绘图区中绘制的点实际上是不变的).于是,点几何中所讲的复数乘点在GeoGebra中其实就是复数乘复数,但要特别注意的是,点乘点是点的数量积,不能理解为复数乘复数.
例4(拿破仑定理)如图6,△ABC中分别以三边为边长同时向外作正三角形△BCD、△CAE及△ABF,其中O1、O2、O3分别是△BCD、△CAE、△ABF的重心,则△O1O2O3为正三角形.
◆8、构造三点A、B、C和三角形t1,输入“t=e^(i*π/3)”得到复数t.
◆9、分别输入“D=C+t*(B-C)”、“E=A+t*(C-A)”、“F=B+t*(A-B)”得到复数D、E、F,将D、E、F的坐标属性修改为“直角坐标”得到三个点;分别输入“Polygon(C,D,B)”、“Polygon(C,E,A)”、“Polygon(A,B,F)”得到三个正三角形t2、t3、t4.
说明:GeoGebra中复数乘点得到的是复数,需要修改坐标属性才能得到点,当然如果将输入指令修改为“D=ToPoint(C+t(B-C))”则可直接得到复数点D;
◆10、分别输入“TriangleCenter(B,C,D,2)”、“TriangleCenter(C,A,E,2)”、“TriangleCenter(A,B,F,2)”,得到三个三角形的重心O1、O2、O3;输入“Polygon(O_2,O_1,O_3)”,得到三角形t5.输入指令“O_1+t*(O_2-O_1)”,得到的复数点与O_3重合,从而得到结论“△O1O2O3为正三角形”.

图6
点几何法证明如下:
要证△O1O2O3为正三角形”,
只要证O3=tO2+(1-t)O1,
又O1、O2、O3为重心,只要证
而D=tB+(1-t)C,E=tC+(1-t)A,
F=tA+(1-t)B,
故而只要证
(1+t)A+(2-t)B=t(1+t)C+t(2-t)A+(1-t2)B+(1-t)(2-t)C,
整理得
(1+t)A+(2-t)B=t(2-t)A+(1-t2)B+[(1-t)(2-t)+t(1+t)]C,
(*)


从而(*)式得证,所以△O1O2O3为正三角形.
应用复数乘点可以简化涉及角度的几何问题,本例当然也可采用复数恒等式方法证明.与例2相类似,有了复数恒等式,我们不但可以压缩证明过程,还可以得到更一般的数学结论[3].
以上,我们以GeoGebra为软件平台,从点的线性运算、数量积、外积和复数乘点四个层面验证了点几何理论的实用价值和独特魅力.一方面,点几何能直观方便地表达基本几何事实,GeoGebra可以更好的阐释点几何的理论构架;另一方面,以点为对象进行操作运算,点几何理论指导下的GeoGebra构造更加快捷高效.事实上,GeoGebra的指令输入,不仅可以对点进行运算,还可以对圆锥曲线、多边形等几何对象进行旋转、放缩等操作.总而言之,点几何理论与GeoGebra实践的融合应用,在彰显点几何的教育价值的同时,为我们在基础教育阶段推行点几何理论开辟了一条路径.
