“以退为进”的教学关键是让学生学会“退”①

崔志荣

(江苏省东台市安丰中学 224221)

1 提出问题

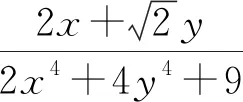
2 教学分析

同一类型问题，学生只能做简单一点的题.说明学生对该类问题有所认识，但不能吃透本质.“以退为进”的教学策略是解决这个现象的好办法，从较难问题退到学生有所认识的问题中，让他们真正吃透问题的本质，从而自然而然地解决问题.“以退为进”也是重要的数学思想方法，它体现了由一般到特殊再到一般的研究思路.因此，数学教学需要培养学生“以退为进”的解题策略，以使学生遇到陌生问题不惧怕.

我国著名数学家华罗庚先生说过：“善于退，足够地退，退到最原始而不失去重要的地方，是学好数学的一个诀窍.”，这充分说明“退”在“以退为进”这种解题策略中的重要性.因此，上述那道数学问题的教学，不仅仅是解决它，要培养学生“以退为进”的解题意识，更要引导学生思考：如何“退”？

3 教学过程

基于以上分析，本文将展示上述那道题的教学过程，强调“以退为进”之“退”的教学引导，与读者交流探讨.

3.1 思想意识的建立

学生未必不能理解“以退为进”这一解题策略，但在实际解决问题中，学生思想意识薄弱，很少有学生运用这一思想方法.因此，解题教学中需要加强培养学生的思想意识，要通过长期的熏陶，让学生自觉运用这样的解题策略.

问题1这道题确有一定难度，为发现其解法，先请同学们学习法国著名数学家、平面直角坐标系的创始人笛卡尔研究“任意一个三角形的重心”的过程，并思考这一研究过程，笛卡尔运用了什么数学思想方法？

投影资料任意一个三角形的重心在哪儿？笛卡尔的想法是，虽然搞不清楚“任意三角形的重心在哪里”，但可以想象把三角形的一个顶点往下压，直到把这个顶点压进另一条边内，这样三角形就变成一条线段.线段的重心在哪儿？当然在中点上.

于是，笛卡尔知道任意三角形的重心在哪儿了.一个三角形可以认为是由一根根长短不一的火柴棍摆起来的，每一根火柴棍就是一条线段，由于每根火柴棍的重心都在它的中点上，所以整堆火柴棍组成的三角形的重心就在三角形的中线上.因此笛卡尔就说，一个三角形的重心一定在一条边的中线上.同理，也在另外两条边的中线上.由于三角形的重心是唯一的，因此三角形三条中线必须交于一点(即重心).由此，笛卡尔不仅发现了三角形的重心，还发现了定理“三角形的三条中线交于一点”.(见文[1])

学生虽然知道笛卡尔所用的思想方法：一般到特殊再到一般.但他们意识不强，有必要用数学家的故事强调思想方法的重要性，熏陶他们的思想意识.这其实就是“以退为进”的解题策略.强调“退”的重要性，进一步熏陶学生的思想意识.而且这种思想方法，教师平时教学中也要经常运用，久而久之的熏陶，学生的思想意识才能真正建立.

问题2“以退为进”是一种重要的解题策略，如何“退”很关键.我们今天研究的这道题有些复杂，请同学们先思考可以从哪些方向“退”？

如果经常运用“以退为进”的解题策略，问题2就不是问题.“退”当然是退到特殊情况，如本题可以“减元”或“降次”，还可以“简化系数”.如果是几何问题，还可以“降维”，也即上文笛卡尔的处理方法.

3.2 一“退”：减元

问题3先从“减元”的角度“退”，这道题可以“退”到什么情况？

3.3 二“退”：降次

问题4再从“降次”的角度“退”，这道题还可以“退”到什么情况？

3.4 三“退”：化系数为1

问题7对于原题，我们已有初步认识，四次单项式与常数项的和用基本不等式可转化为二次单项式，而二次单项式与常数项的和再用基本不等式可转化为一次单项式，由此可求最大值.同学们先试着完成，看看还会遇到什么困难.

问题8原题的系数过于复杂，能不能从系数的角度思考，将系数“退”至简单的情况，以便用待定系数法，由取等条件容易求出待定系数？

后，仍无法处理.

问题9请同学们思考，经过两次运用基本不等式后，怎样才能得到最大值？能不能再“退一退”系数？

两个关于x项的处理完全一致，且与y项的处理也一致.于是，上述待定系数m,n应该相等，即

已将系数退至简单情况，利用待定系数法很容易将常数分拆，甚至能直接看出. 由

3.5 回归本质

问题10以上我们通过“以退为进”的策略，已分析出2次运用基本不等式解决问题，且解决了待定系数法运算困难的问题，先请同学们整理一下解题过程，再回顾思考我们“以退为进”流程，以及命题者的命题流程.

学生都能整理解题过程，

所以当且仅当x=y=1时，

得到解题处理方法.

4 结束语

“授人以鱼不如授人以渔”，即让学生学会运用数学思想方法解决问题，比教会学生数学知识更重要.“以退为进”是探究陌生数学问题的重要思想方法，我们应把这种重要的思想方法作为解题教学的重点.在解题教学中，要不怕费时，引导学生学会“退”，让他们足够地“退”，通过长期的熏陶，逐步建立学生“以退为进”的思想意识，由此培养学生主动探究陌生问题的勇气和决心、培养学生能够解决较难问题的能力.