一组合几何问题的证明和推广

孙 泰

(北京市丰台区第二中学 100071)

2017年8月10日晚，华南师范大学吴康教授在朋友圈发帖，公布数学家杨路教授在朋友圈发布征求一个几何命题的初等证明的帖子：

命题一个平面凸四边形，经过每三个点可作一个圆，这样得到4个圆(不排除其中有重合)，求证：4个圆中如果有3个相等，则此4顶点共圆.

帖子发出，迅速得到余泽伟老师、朱斌老师、李荣峰老师、骆来根老师及本人的解答.

本题简洁优美，证法多样，余味不绝，遂探究推广，幸得点滴，下以示之，望得指点.

引理1若△ABC和△ABD外接圆是等圆且不重合，则C、D在AB同侧时，∠ACB+∠ADB=180°；C、D在AB异侧时，∠ACB=∠ADB.

(如图1)由同圆或等圆中，等弧所对应的圆周角相等，及圆内接四边形对角互补容易得之.

引理2△ABC三个顶点与点D构成平面凸四边形，若△ABD、△ACD与△ABC外接圆相等，则A、B、C、D四顶点共圆.

证明分两种情况.

情况1：(如图2)若△ABD、△ACD与△ABC外接圆相等且不重合，否则A、B、C、D四顶点共圆.

由引理1知∠ADB+∠ACB=180°, ∠ADC=∠ABC,且∠ADB<∠ADC，于是∠ABC+∠ACB>180°，那么与△ABC内角和等于180°矛盾，必有A、B、C、D四顶点共圆.

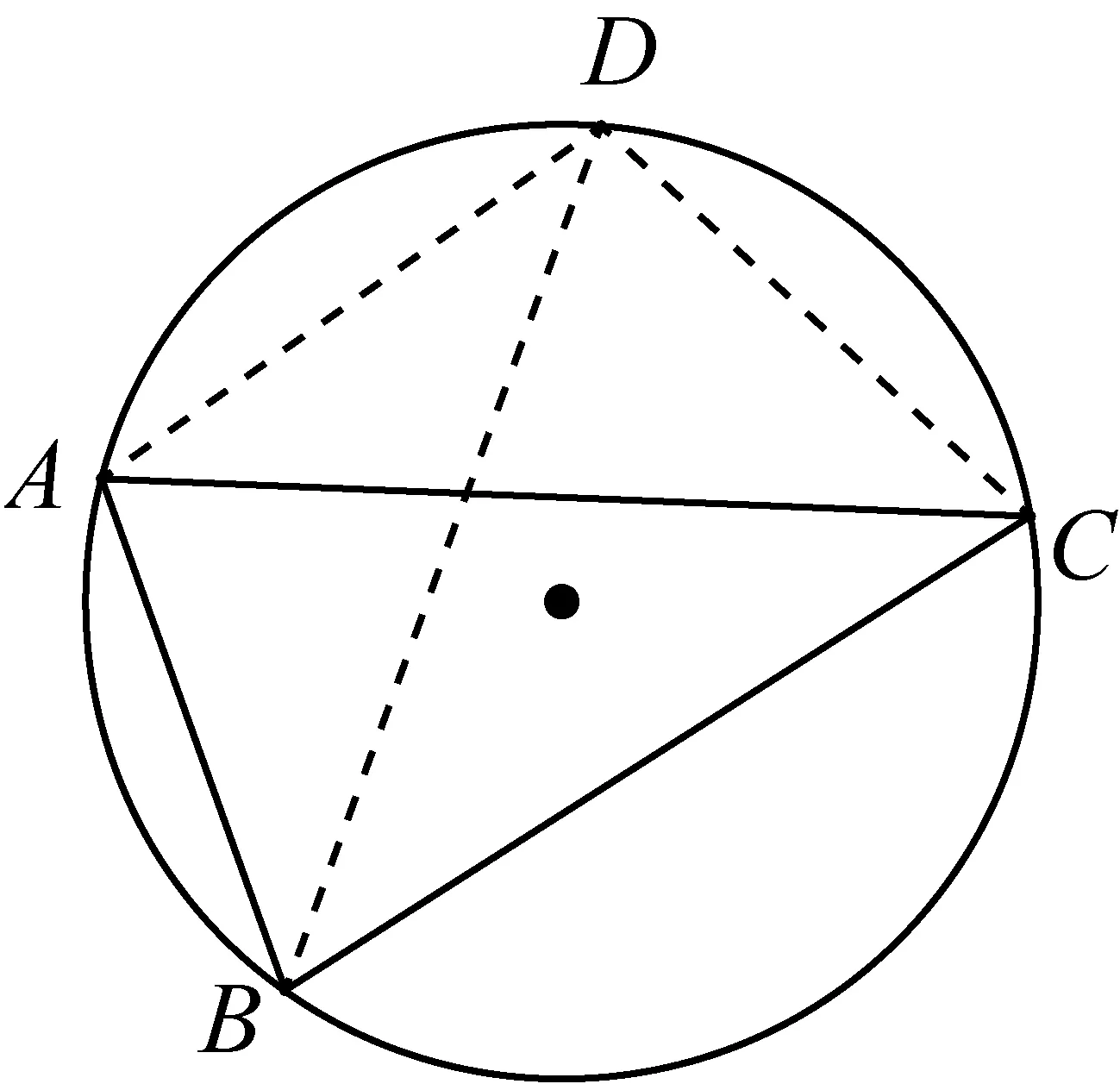
图2

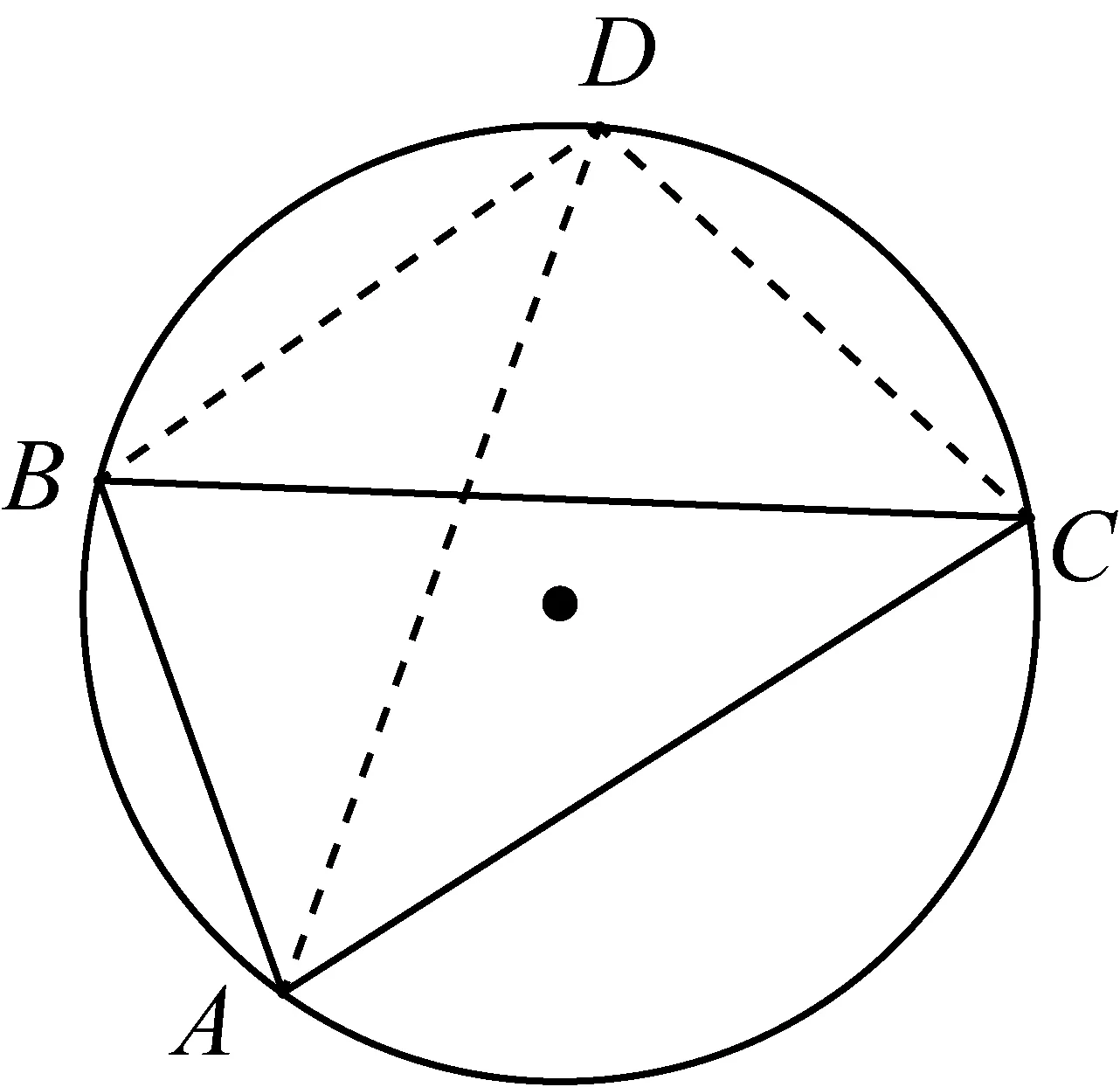
图3

情况2：(如图3)若△ABD、△ACD与△ABC外接圆相等且不重合，否则A、B、C、D四顶点共圆.

由引理1知∠ADB+∠ACB=180°, ∠ADC+∠ABC=180°，那么凸四边形ABCD内角和必大于360°，与平面凸四边ABCD不符，必有A、B、C、D四顶点共圆.

注：此引理等价于杨路教授提出的命题.

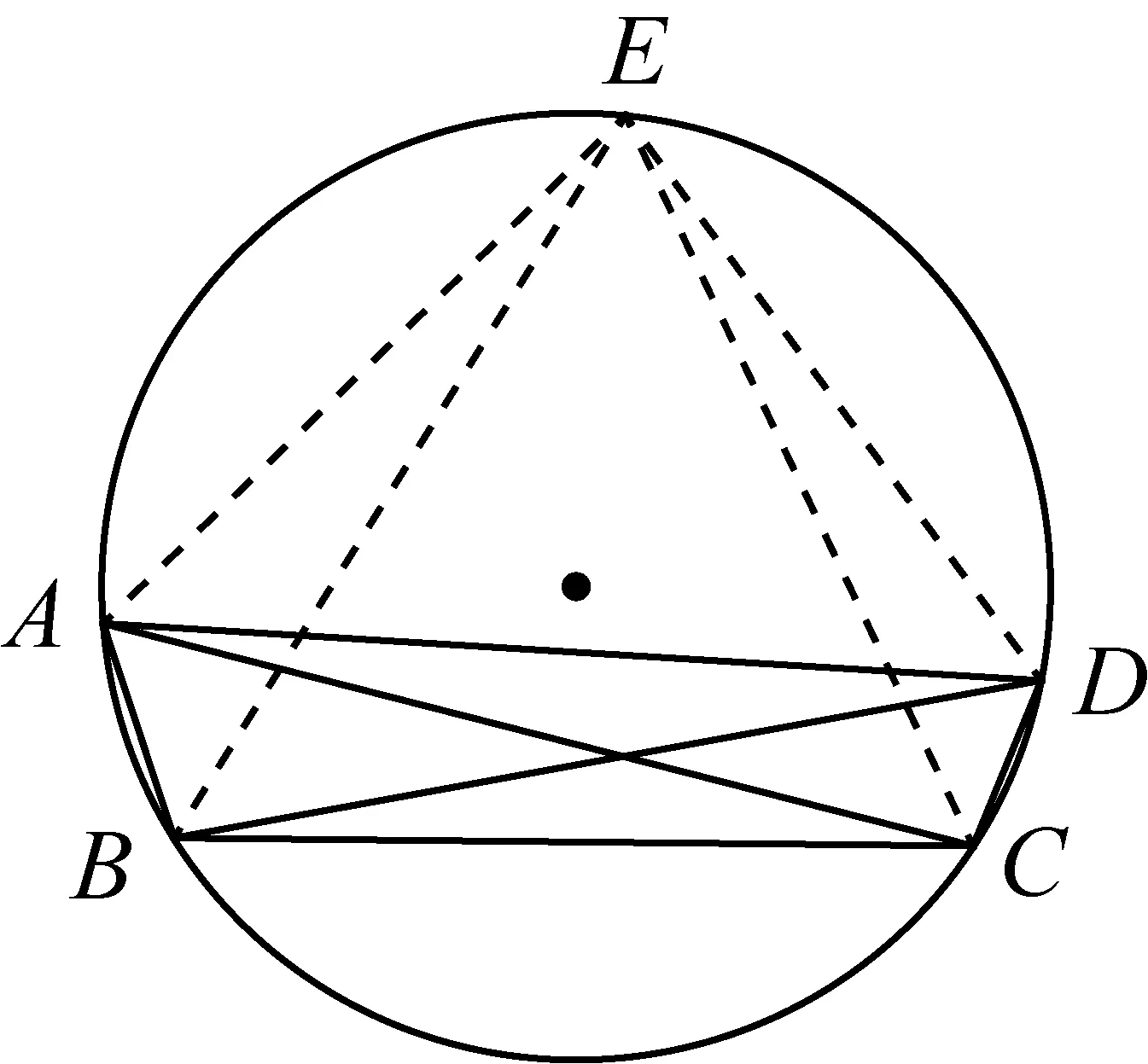
图4

引理3如图4,⊙O内接四边形ABCD与点E构成平面凸五边形ABCDE，若△ABE、△ACE外接圆与⊙O相等，或若△ABE、△CDE外接圆与⊙O相等，或若△BCE、△ADE外接圆与⊙O相等，则A、B、C、D、E五顶点共圆；若△ACE、△BDE外接圆与⊙O相等,A、B、C、D、E五顶点未必共圆.

证明情况1：△ABE、△ACE外接圆与⊙O相等，由引理2知A、B、C、E四点共圆，则A、B、C、D、E五顶点共圆；

情况2：(如图4)若△ABE、△CDE外接圆与⊙O相等，假设△ABE、△CDE外接圆与⊙O相等且不重合，由引理1知∠AEB+∠ACB=180°，∠CED+∠CBD=180°，所以∠ACB+∠CBD=180°,∠AEB+180°,∠CED>180°，得四边形ABCD内角和大于360°，与平面凸四边ABCD不符，那么△ABE、△CDE外接圆中至少一个与⊙O重合，所以A、B、C、D、E五顶点共圆.

情况3：(如图4)若△BCE、△ADE外接圆与⊙O相等，假设△BCE、△ADE外接圆与⊙O相等且不重合，由引理1知∠BEC+∠BAC=180°，∠AED=∠ABD,又平面凸五边形ABCDE知∠AED>∠BEC,因此∠ABD+∠BAC=180°-∠BEC+∠AED>180°，得四边形ABCD内角和大于360°，与平面凸四边ABCD不符，那么△BCE、△ADE外接圆中至少一个与⊙O重合，所以A、B、C、D、E五顶点共圆.

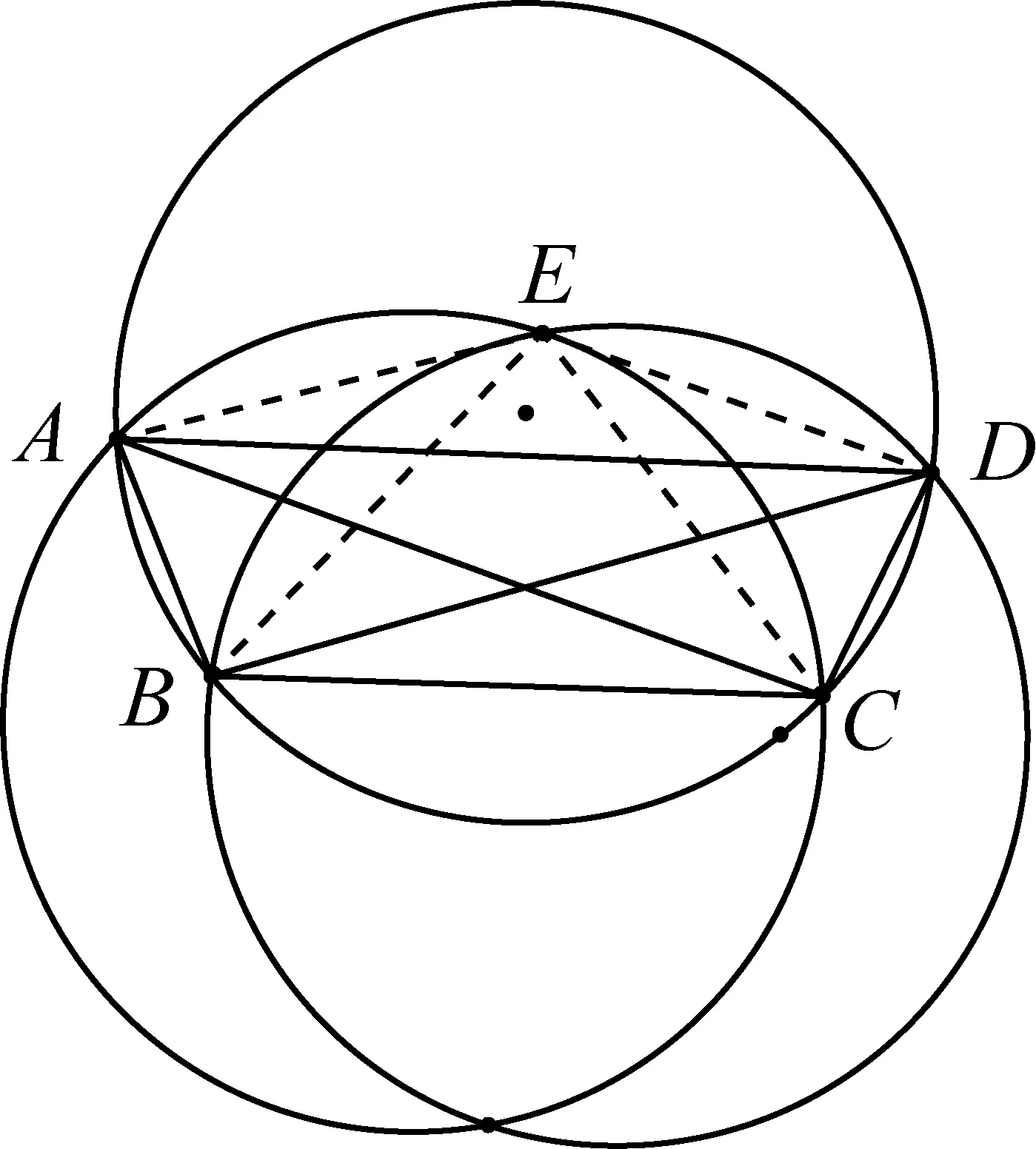
图5

情况4：(如图5)若△ACE、△BDE外接圆与⊙O相等,如图，A、B、C、D、E五点不共圆.

注：情况4中有6个相等圆.

下面先探究特殊情况，得到：

命题1一个平面凸五边形，经过每三个点可作一个圆，这样得到10个圆(不排除其中有重合)，求证：10个圆中如果有7个相等，则此5顶点共圆.

为叙述方便，下文我们把外接圆相等的三角形简称“等圆三角形”

证明先证5顶点中必存在4个顶点共圆.

假设每个顶点所在的“等圆三角形”至少有5个，每个“等圆三角形”至多被计算3次，那么“等圆三角形”至少有5×5÷3>8个，与已知7个“等圆三角形”矛盾.故必存在一个顶点(不妨A)，含此顶点的“等圆三角形”不超过4个，那么剩下4个顶点至少有3个“等圆三角形”，由引理2知，此4个顶点共圆.

注：由引理3的情况4可知7个“等圆三角形”是最佳值.

命题2一个平面凸六边形，经过每三个点可作一个圆，这样得到20个圆(不排除其中有重合)，求证：20个圆中如果有13个相等，则此6顶点共圆.

证明先证6顶点中必存在5个顶点共圆.

假设每个顶点所在的“等圆三角形”至少有7个，每个“等圆三角形”至多被计算3次，那么“等圆三角形”至少有7×6÷3=14>13个，与已知13“等圆三角形”矛盾.故必存在一个顶点(不妨A)所在的“等圆三角形”不超过6个，那么剩下5个顶点至少有7个“等圆三角形”，由命题1可得，则此5个顶点共圆.

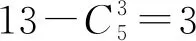
归纳猜测命题的一般情况：

证明下用数学归纳法仅需证明n≥5此命题成立.

(1)当n=5时,由命题1知命题成立.

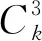
那么n=k+1时，先证平面凸k+1边形存在k个顶点共圆.

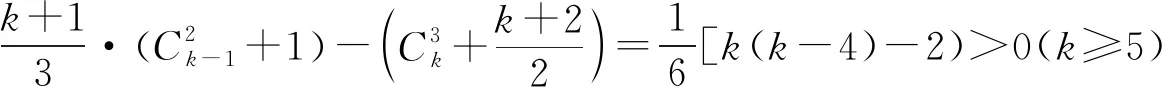
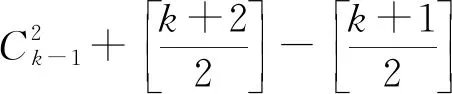
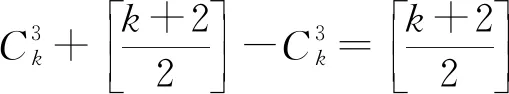
综合由(1)、(2)可知命题成立.

完成二维条件下的探究和推广，自然思考三维空间情况，最后提出如下问题：