基于离散天牛群算法的高桩码头传感器优化布置
2020-06-23胥松奇周世良曹师宝皮东衢
胥松奇,周世良,曹师宝,皮东衢
(1.重庆交通大学,重庆 400074;2.重庆西南水运工程科学研究所,重庆 400016;3.重庆交通运输控股(集团)有限公司,重庆 401121)
随着基础建设的飞速发展,我国已成为水运大国与水运强国,码头保有量位居世界前列。码头结构在使用过程中由于碰撞、疲劳、过载、不均匀沉降等因素[1],不可避免会出现一些损伤,给码头结构的安全埋下隐患。且码头结构日益朝着大型化、专业化方向发展,这些码头结构的健康状况与重大安全问题密切相关。因此,进行有效的码头结构健康监测,实时了解码头结构的健康状况,并在结构损坏前发出安全警告是十分必要的。
一般来说,结构健康监测系统主要包括3个部分,即:数据采集终端、数据传输网络和数据处理中心。通过在结构关键部位安装适当数量的传感器,可以收集响应信息,如结构的位移、速度和加速度。通过科学的数值计算,对该结构的健康状况进行评价,并为结构的日常维护、安全和耐久性分析提供重要的参考依据,使结构更好地服务于经济建设。因此,数据采集的质量直接影响到结构健康监测系统的准确性,正确安装结构关键部位的传感器以获得最有效的数据是结构健康监测系统的基础与关键[2]。
由于国内码头结构健康监测理念起步较晚,目前学者们着重开展码头结构健康监测技术方面的研究[3-5],而针对高桩码头的传感器布置仍处于基于工程师个人经验的阶段,具有较强的盲目性。国内仅张迅等[6]采用自适应遗传算法开展了高桩码头传感器优化布置研究,取得了一定的效果,但遗传算法存在计算复杂、初始参数难以确定、对初始种群依赖性强、算法收敛速度慢等缺点。因此,需要研究一种新的高桩码头传感器优化布置方法。
本文采用“0-1”编码的方法,引入位置变换概率的思想和离散化天牛群算法,基于模态置信度准则,提出了一种基于离散天牛群算法的高桩码头传感器优化布置方法。以某高桩码头为例,开展了优化布置方法的运用研究,并与传统的离散粒子群算法进行了对比分析。结果表明该方法在高桩码头传感器优化布置上的适用性与有效性,较传统离散粒子群算法更具优势。
1 高桩码头传感器优化布置的数学模型
在高桩码头结构健康监测中,首要任务是确定传感器测点位置,以获得码头结构的响应数据。然而,在高桩码头中,可布设传感器的测点位置较多,获得所有测点处的响应数据显然是不现实的。因此,如何在传感器数目一定的情况下,开展高桩码头传感器优化布置的研究是必要的,这不仅能获得最有价值的结构响应信息,还能够有效节约经济成本。
在传感器优化布置中,许多学者普遍采用有效独立准则(EI)、模态动能准则(MKE)和模态置信度准则(MAC),本文拟采用模态置信度准则。模态置信度准则在选择测点位置时,保证所选测点测得的模态向量之间有较大的空间交角,以尽可能保留原结构的特征。模态置信度准则中采用模态置信度矩阵(modal assurance criterion,简称MAC矩阵)来评价模态向量空间夹角,其矩阵元素表达式为:
(1)
式中:φi和φj分别为第i阶和第j阶模态振型向量。模态置信度矩阵的一个非对角元MACij(i≠j)⊂(0,1),它能反映出第i阶和第j阶模态振型向量的可辨性,其值越小(越接近0),两模态振型向量之间的可辨性越好,传感器放置的效果越好。
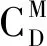
fit(x)=min(max(MACij)) (i≠j)
(2)
式中:x为一个有D个“0”和“1”元素的数组,其中包含M个“1”,(D-M)个“0”。“1”和“0”代表是否提取振型向量,即是否在该测点布置传感器。
fit(x)即为问题的适应度函数,解出式(2)中fit(x)取最小值时所对应的数组x,即能得到传感器最优布置位置。
2 离散天牛群算法
2.1 仿生原理
当天牛觅食时,天牛并不知道食物位置,而是根据食物散发出的气味强弱来进行觅食。天牛利用两只触须来探测食物气味,如果左须接收到的气味强度比右须大,那下一步天牛就往左飞,否则就往右飞。依据这一原理天牛可以快速有效地找到食物。天牛通过触须探测食物气味从而搜寻到食物的过程见图1。

图1 天牛觅食过程
受到天牛觅食原理的启发,将天牛觅食模型由3维空间推广到D维空间,Jiang等[7]提出了一种有效的智能优化算法——天牛须搜索(BAS)算法,因其易于实现、收敛速度快及不易陷入局部极值等特点,受到了学术界的关注。Wang等[8]借鉴群体智能的思想优化了BAS算法提出了天牛群(BSO)算法,进一步提高了算法的收敛精度。
2.2 离散处理方法
传统的BAS与BSO算法只适用于连续函数的优化问题,而高桩码头传感器优化布置属于典型的“0-1”离散问题。x=[x1,x2,...,xD]表示某只天牛的位置,是一个只包含“0”和“1”元素的数组,即一种传感器布置方法;v=[v1,v2,...,vD]表示某只天牛的速度。针对高桩码头传感器优化布置这一具体的离散问题,通过式(3)将天牛的速度值vi转化为“0-1”变换的概率s(vi)[9]:
(3)
式中:s(vi)为解x数组中的某个元素xi取1的概率,即在该点布置传感器的可能性大小,s(vi)越大,xi取1的概率越大,越有可能在该点布置传感器。
根据以上定义,xi的表达式可用式(4)表示:
(4)
式中:rand()为[0,1]上的随机数。
根据已知传感器的个数M,结合式(4),将s(vi)与rand差值较大的前M个xi取为1,其余(D-M)个xi取为0,即完成了天牛的位置变换。
2.3 算法实现
根据前述的高桩码头传感器优化布置数学模型与天牛群算法的离散化处理方法,基于离散天牛群算法的高桩码头传感器优化布置的流程见图2,具体步骤如下:
第1步:初始化算法的计算参数。包括传感器个数M、可布设传感器测点数D、天牛群中天牛只数N、最大迭代次数max_DT、天牛速度上下限vmax和vmin、天牛速度学习因子c1和c2。
第2步:初始化天牛群位置xND及其速度vND。对每只天牛,将其位置x中的任意M维变为1,其余(D-M)维为0;将其速度v的每1维生成[vmin,vmax]上的随机数。根据式(2)计算每只天牛位置所对应的适应度函数fit(x),用P记录天牛群的个体最优位置,Pg记录全局最优位置,此时的P=Pg。
第3步:迭代计算。对每只天牛,通过式(5)更新其左右须对应速度:
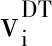
(5)
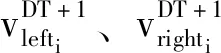
通过式(3)将天牛的左右须速度值vlefti、vrighti转化为“0-1”变换的概率s(vlefti)、s(vrighti)。通过式(4)将s(vlefti)、s(vrighti)与rand差值较大的前M个xi取为1,其余(D-M)个xi取为0,生成天牛左右须探测到的食物位置xleft、xright,并计算其所对应的适应度函数fit(xleft)、fit(xright)。
第4步:迭代计算中天牛的“食物气味强度判断”。判断fit(x)、fit(xleft)、fit(xright)三者大小,若fit(xleft)最小,则更新天牛位置x=xleft;若fit(xright)最小,则更新天牛位置x=xright;若fit(x)最小,则通过式(3~5)天牛随机移到位置x。同时更新P和Pg。
第5步:迭代停止判断与结果输出。若DT=max_DT,则输出Pg和fit(Pg),否则转至第3步继续进行迭代计算。
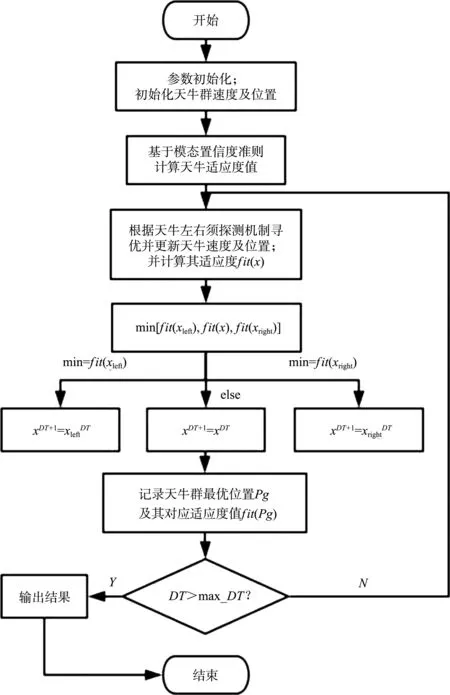
图2 离散天牛群算法高桩码头传感器优化布置流程
3 工程实例分析
3.1 工程概况
针对某高桩码头结构,取其基本结构横向排架作为概化单元进行分析。横梁长10 m,桩长50 m,土体以上的桩长为30 m,横梁为混凝土T型梁,尺寸见图3,桩基为钢管混凝土摩擦桩,桩身直径1.2 m,上层土体为粉砂质黏土,深10 m,土体抗力系数M1取2.5 MN/m4,下层土体为粗砂质黏土,土体抗力系数M2取6.0 MN/m4。横向排架整体结构见图4。

图3 横梁断面(单位:mm)
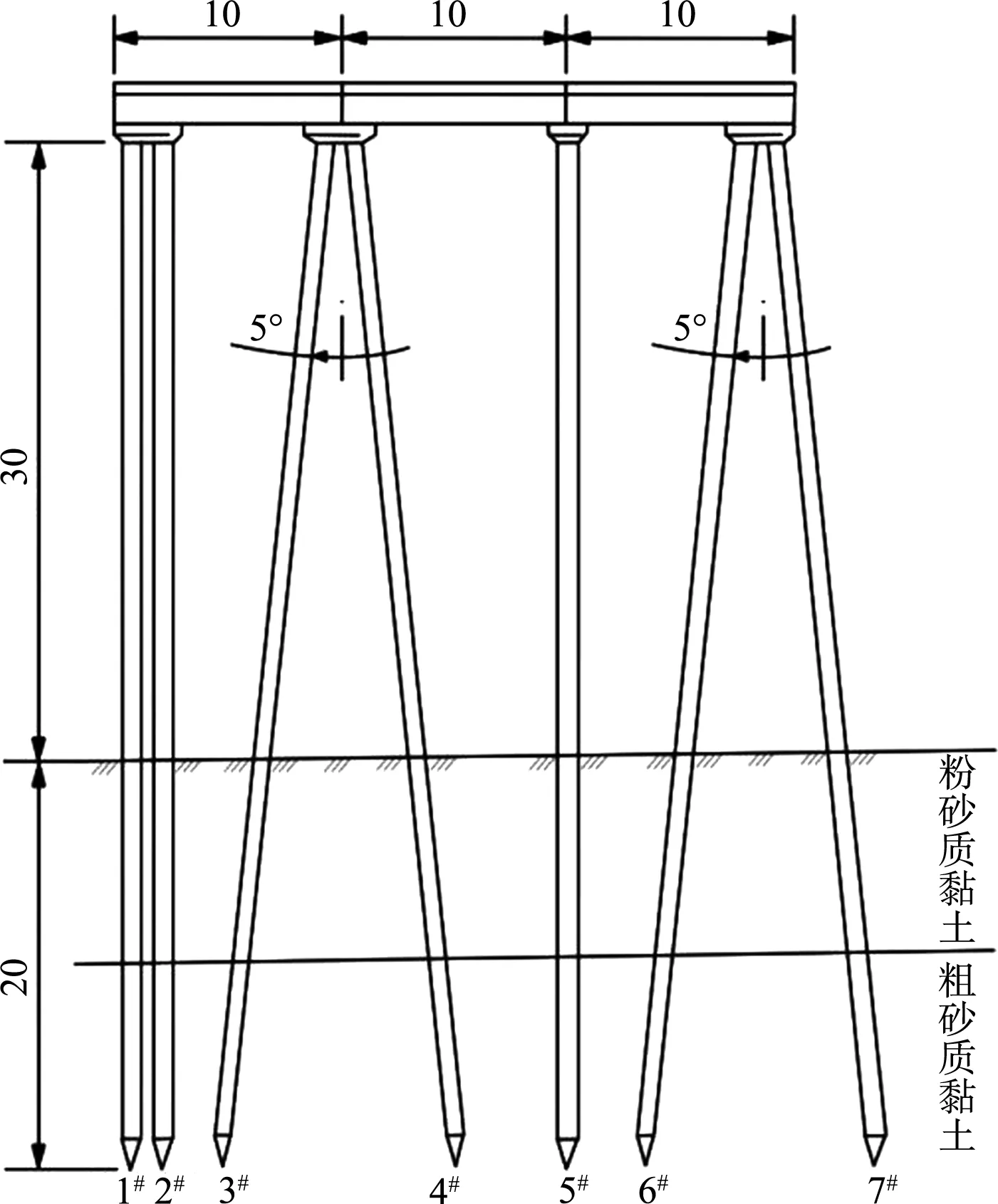
图4 横向排架结构(单位:m)
3.2 数值建模
采用大型通用有限元分析软件ABAQUS建立高桩码头横向排架有限元模型。钢筋混凝土材料杨氏模量取21 GPa,泊松比取0.2,密度取2.5 t/m3。桩土相互作用采用土弹簧模型模拟。考虑码头中间部分横向排架受两侧纵梁约束,垂直于纸面方向不发生变形和振动,所以排架的横梁和桩单元类型均选择B21平面梁单元。为计算方便,每1 m划分1个单元,模型共380个单元、381个节点,单元划分越多计算越精确。拟在桩基上进行传感器布置,每根桩基位于泥面以上的节点共29个,7根桩基共203个节点可布设传感器。按1~203的顺序对1#~7#桩基泥面以上节点进行编号,以便于传感器定位。横向排架有限元模型见图5。

图5 横向排架有限元模型
3.3 模态分析
采用ABAQUS中的线性摄动分析步对高桩码头横向排架进行模态分析,取其前8阶模态振型进行研究(仅列出前4阶模态振型,见图6),前8阶模态振型对应的频率见表1,同时提取了前8阶模态振型所对应的模态振型向量作为采用模态置信度准则进行传感器优化布置的依据(注意到高桩码头横向排架的振动主要发生在x方向,故此处只提取x方向的自由度U1组成模态振型向量)。

表1 高桩码头横向排架前8阶模态振型对应频率
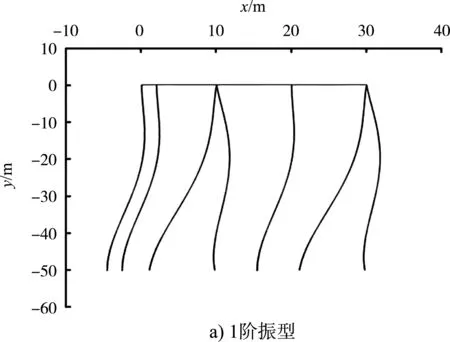
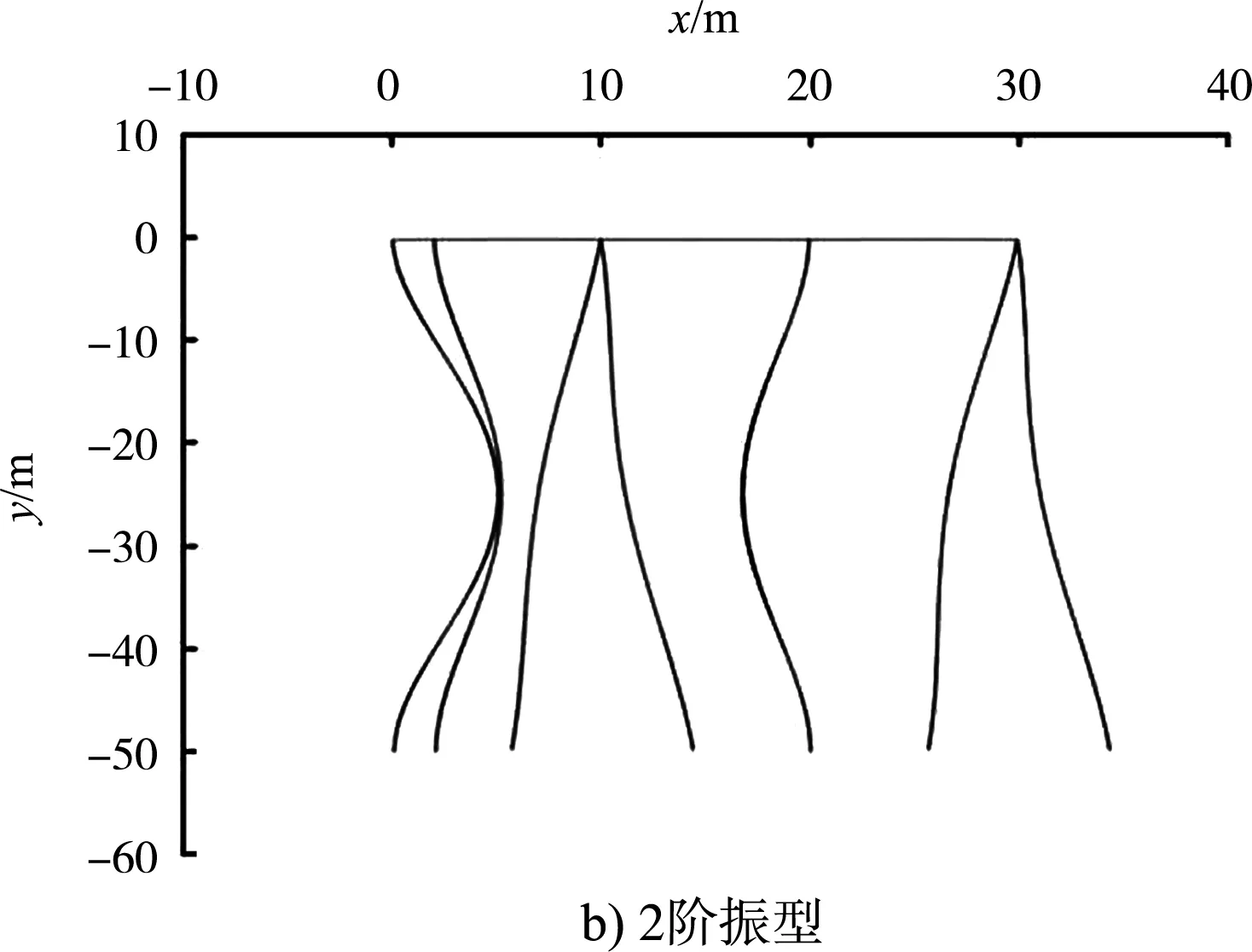
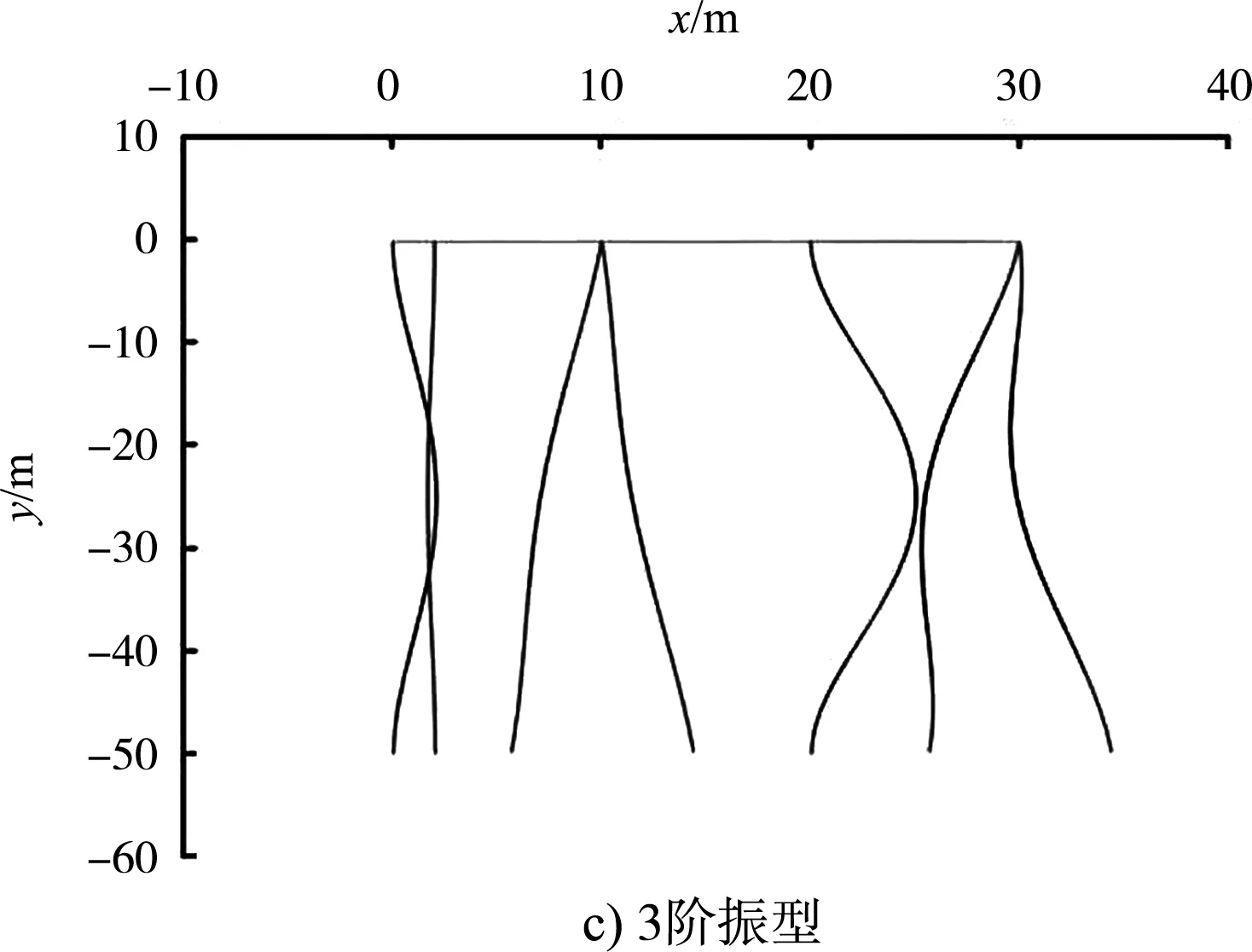
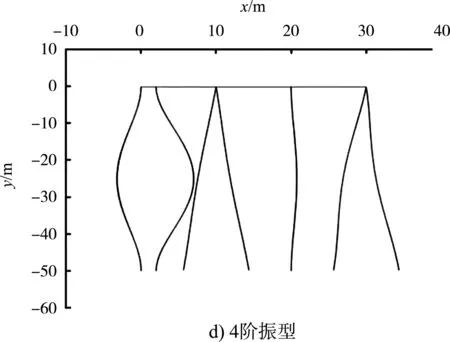
图6 高桩码头横向排架前4阶模态振型
3.4 基于离散天牛群算法的传感器优化布置
3.4.1计算参数

表2 BBSO算法计算参数
3.4.2迭代过程
为了验证BBSO算法在高桩码头横向排架传感器优化布置中的表现,同时采用了文献[9]中的传统离散粒子群(BPSO)算法进行求解作为对比,计算结果取10次计算的最优值。BBSO算法与BPSO算法迭代过程中,适应度函数——MAC矩阵最大非对角元变化曲线见图7,迭代完成后最佳传感器布置位置所对应的MAC矩阵见图8。
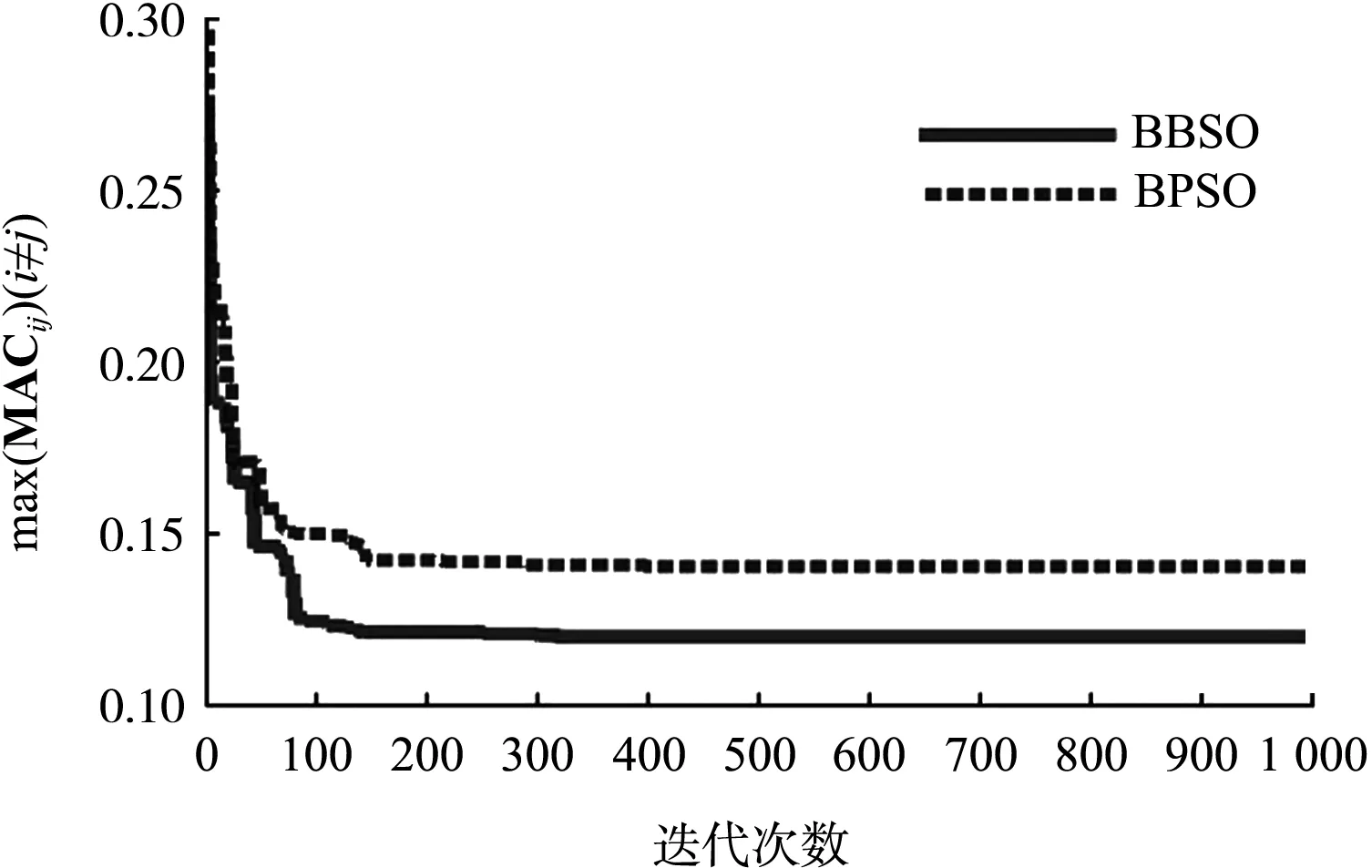
图7 MAC矩阵最大非对角元迭代变化曲线
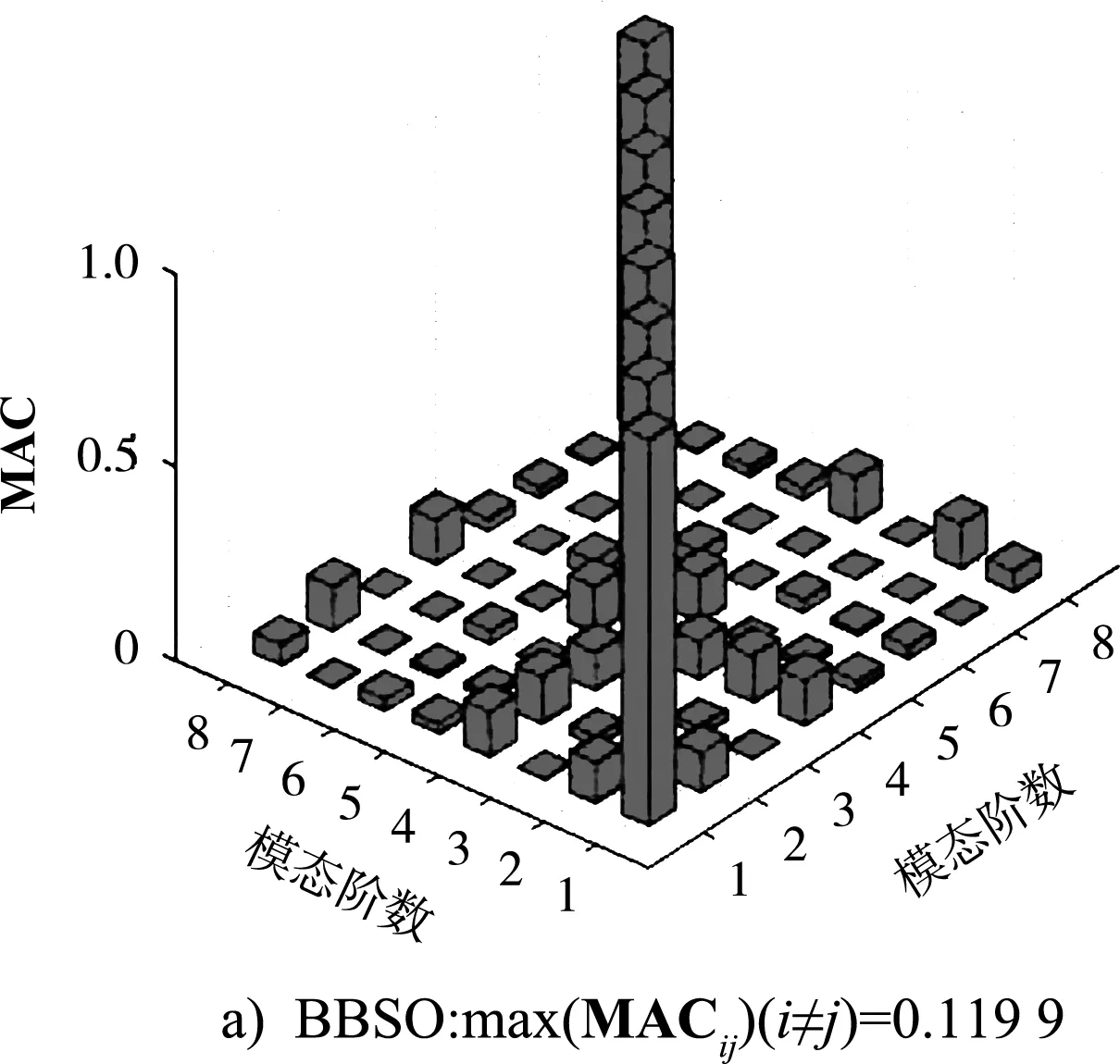
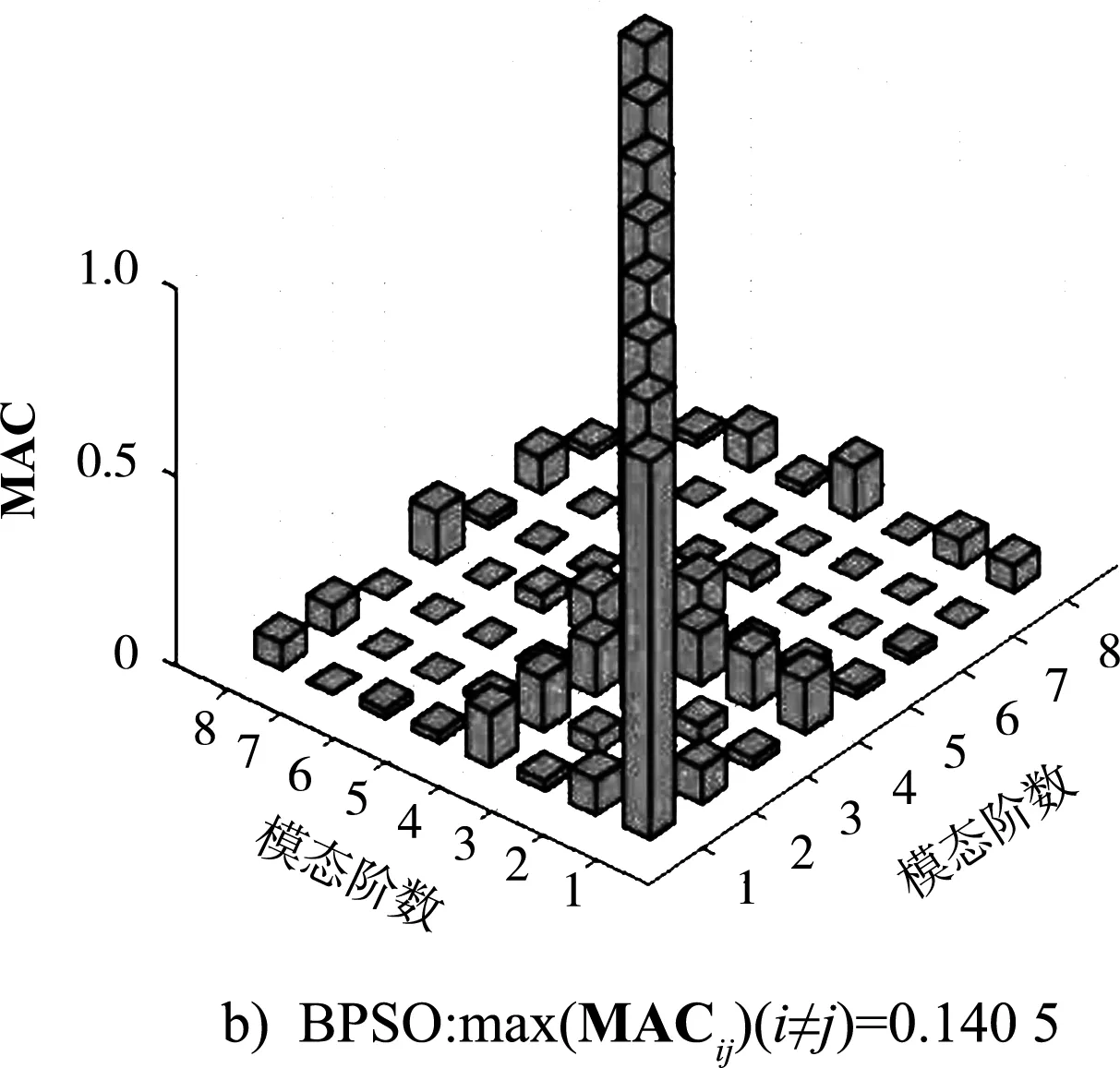
图8 最佳传感器布置位置所对应的MAC矩阵
从图7可以看出,相比于传统BPSO算法,本文提出的BBSO算法提高了计算的收敛速度与收敛精度。BBSO算法快速收敛,在第80代左右便进入了局部搜索,在第320代左右收敛到了最优值;而BPSO算法在140代左右还有较为明显的“下降台阶”,且在第300代左右陷入了局部极值。究其原因,BBSO算法的优势得益于BBSO算法利用了天牛用左右须探测食物气味浓度,通过判断,从而进行移动的仿生原理。
3.4.3优化计算分析
从图8可以看出,BBSO算法与BPSO算法计算得出的最佳传感器布置位置所对应的MAC矩阵的非对角元均接近于0,即模态向量间的夹角趋于正交,所选择的布置传感器的测点测得的结构模态信息易于辨识。且BBSO算法计算得出的最佳传感器布置位置所对应的MAC矩阵的最大非对角元为0.119 9,较BPSO算法计算得出的值0.140 5更小。为进一步分析,将各阶模态振型在MAC矩阵中的最大非对角元绘于图9中。从图9可以看出,BBSO算法结果除第5阶模态振型在MAC矩阵中的最大非对角元较BPSO算法结果大以外,其余7阶模态振型在MAC矩阵中的最大非对角元均小于BPSO结果。BBSO算法结果MAC矩阵的最大非对角元恰好出现在第5阶模态振型,而BPSO算法结果出现在第4阶。
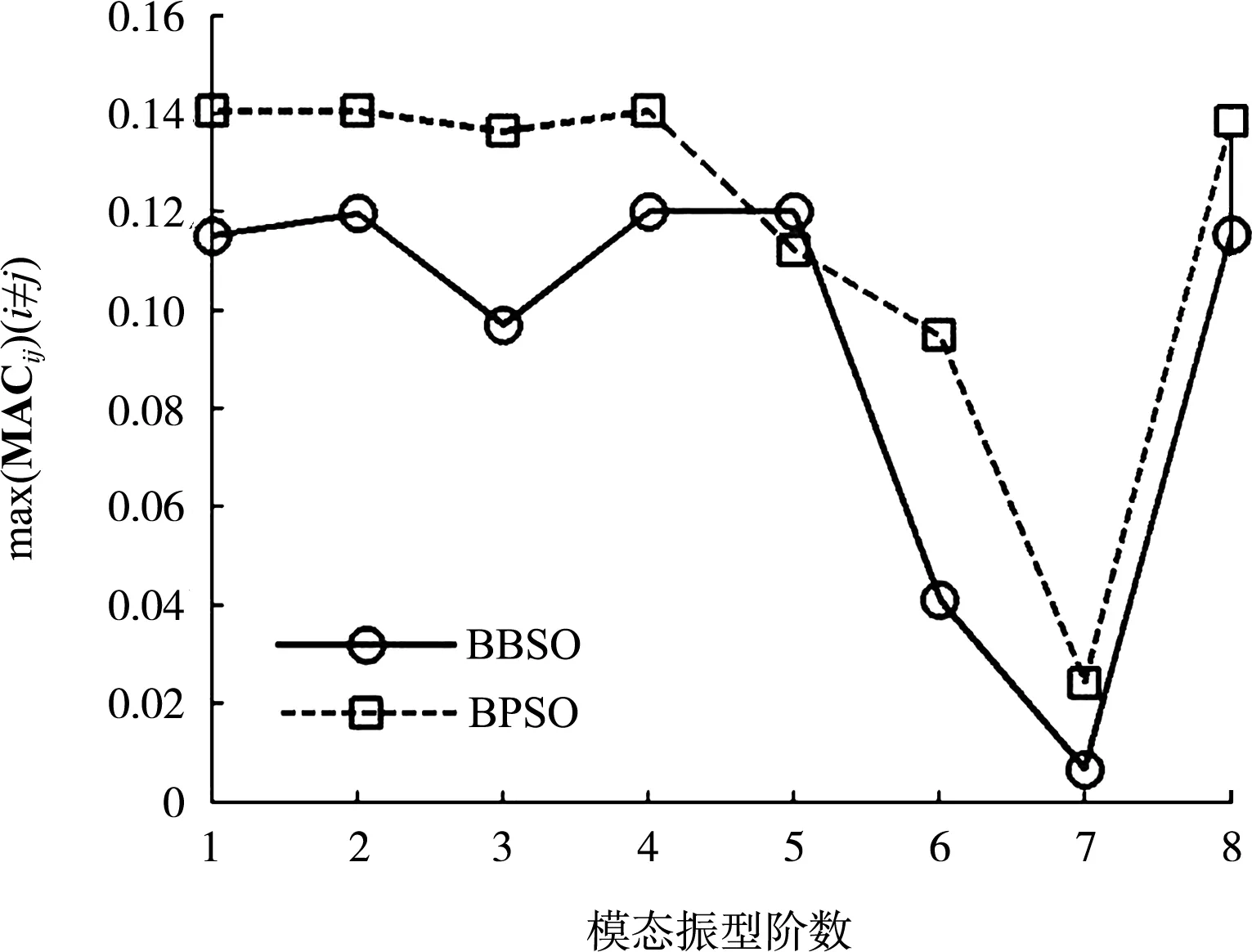
图9 各阶模态振型MAC矩阵最大非对角元
3.4.4优化布置方案及评价
根据BBSO算法迭代完成后得到的最优数组x中的“1”元素进行定位,返回“1”元素在x中出现的序号:
x_index=[16,85,108,120,126,140,150,155,156,172,179,191 ]
(6)
x_index即表示最优传感器布置位置所对应的节点编号,因此,此高桩码头横向排架最优传感器布置方案见图10。从图10可以看出,高桩码头横向排架传感器主要集中布置在后排桩基上部位置。整体来说,后排桩基传感器覆盖密度较前排大。对于后排桩基,桩基上部传感器覆盖密度较下部大;对于前排桩基,桩基下部传感器覆盖密度较上部大。
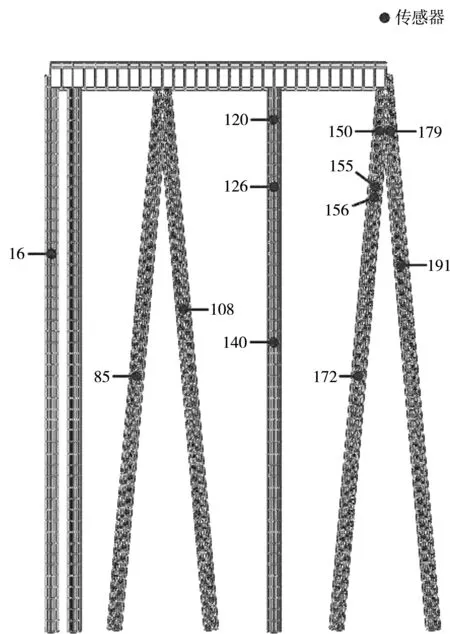
图10 最优传感器布置位置及其对应节点编号
4 结论
1)利用本文提出的基于离散天牛群算法的高桩码头传感器优化布置方法,得到了某高桩码头横向排架7根桩基的传感器布置方案,通过对布置方案测点结果进行评估,模态向量间的夹角趋于正交,证明传感器布置方案有效。
2)本文所提出的基于离散天牛群(BBSO)算法的高桩码头传感器优化布置方法较传统离散粒子群(BPSO)算法在收敛速度和收敛精度上更具优势。
3)通过对高桩码头横向排架7根桩基的传感器布置方案分析发现,高桩码头横向排架传感器覆盖密度呈“后排桩基大于前排桩基,后排桩基上部大于下部,前排桩基下部大于上部”的分布形式。
