斜坡型潜导堤波浪力特性的数值研究*

黄昭培,肖 乐,陈 乾,杨成刚

(1.河海大学 港口海岸与近海工程学院，江苏 南京 210098；2.武汉综合交通研究院有限公司，湖北 武汉 430000)

20世纪60年代至今，国内已有很多港口和外航道在建设中采用防沙堤、导流堤，目前潜堤形式的防沙堤和导流堤在这类工程中较为常见，潜堤断面形式较多，有斜坡型、半圆形、矩形、梯形等，在实际工程中多采用半圆形和斜坡型。尽管在实际河口海岸工程中潜堤已得到应用，但潜堤上的波浪力、潜堤的消浪以及如何选取合理的断面形式与尺度仍是潜堤研究的一个重要问题。

目前国内外对潜堤的研究多针对透浪系数、波浪场等水动力特性[1-4]，研究其受力还较少，对波浪作用下潜堤所受波浪力的研究大多采用Froude-Krylov理论解析及物理模型试验的方法展开。针对Froude-Krylov理论中的绕射系数，Herbich[5]建议长方潜体的水平绕射系数CH为1.8～2.0、垂直绕射系数CV为2.7；Hogben等[6]对于圆柱潜体，通过模型试验给出圆柱潜体的绕射系数CH和CV值；Garrison等[7]给出半球潜体在不同相对水深、不同相对半径情况下的CH和CV值；《防波堤与护岸设计规范》[8]仅体现计算半圆形防波堤波浪力公式，还缺少经验公式对其他类型潜堤断面进行波浪力估算；Westphalen等[9]采用计算流体力学软件，对线性波浪作用下半淹没圆柱上的波浪力进行数值计算，其结果与试验数据吻合较好；Hu等[10]利用数值波浪水槽模型对线性波浪作用下半淹没水平圆柱的受力进行计算，其结果与试验结果吻合较好；Chen等[11]对部分淹没水平圆柱和方柱上的波浪力进行计算，发现入射波波长越长，惯性力越小；饶永红等[12]针对半圆形潜堤波浪力特性，通过物理模型试验模拟不规则波与潜堤的相互作用过程，测定并拟合出半圆形潜堤波浪力的计算公式；刘圆[13]针对矩形潜堤波浪力特性，通过物理模型试验总结出潜堤波浪力特性的变化规律，并提出相应的矩形潜堤波浪力的经验公式；胡宝琳等[14]针对波浪荷载作用下的斜坡式潜堤结构，从堤前波浪的入射和反射入手，推导出斜坡式潜堤上波浪力的解析方程，并将解析方程计算结果与通用数值计算软件FLUENT的计算结果进行对比分析；刘必劲等[15]基于约束内插方法(CIP)，采用 流体体积(VOF)两相流模型，对潜堤波浪传播等水动力特性进行试验与数值研究。

从上述国内外研究可看出，目前有关潜堤所受波浪力的研究仅依靠理论分析和数值计算，缺少物理模型试验验证，或是没有考虑相关要素对波浪力特性的影响，或是仅针对半圆形和矩形潜堤所受波浪力研究，缺少对斜坡式潜堤所受波浪力特性的研究分析，且相应潜堤波浪力的计算公式也较少。因此针对上述研究的局限性，同时借鉴邹恒[16]对于海堤挡浪墙波浪力数值计算研究的成果经验，本文以某防沙双导堤工程物理模型试验结果为依据，基于黏性不可压缩气液两相流理论，采用FLUENT数值模拟软件对该斜坡型潜导堤所受波浪力进行数值计算，分析研究淹没水深和波高这两要素对潜导堤迎浪面与堤顶面上所受波浪力特性的影响，经对试验数据的整理和分析，拟合得到斜坡型潜导堤堤顶面最大波浪力计算公式，为类似的实际工程断面设计提供理论依据。

1 工程方案

1.1 潜导堤断面设计方案

斜坡型防沙潜导堤结构为：防沙堤内、外侧护坡及堤顶均采用四脚空心方块护面，堤心采用10～100 kg块石，护面与堤心之间采用100～200 kg、150～200 kg块石垫层，堤身两侧边坡均为1:1.5，护底采用块石+砂肋软体排结构形式，四脚空心方块护面下方设置混凝土镇脚块。斜坡型防沙潜导堤的断面结构见图1。

图1 斜坡型潜导堤横断面(高程：m；尺寸：mm)

1.2 设计水位及波要素

潜导堤设计水位(以当地理论基准面为基准)：极端高水位为4.83 m(重现期为50 a一遇，下同)，设计高水位为2.60 m，设计低水位为0.27 m。各级水位下，重现期为50 a一遇设计波浪要素见表1。

表1 潜导堤前设计规则波波要素

1.3 物理模型试验

物理模型试验的主要内容为工程断面在相应水位及对应规则波波要素条件下稳定性的检测及潜导堤所受波浪力的测定。试验结果表明：工程断面均能在试验工况条件下保持稳定。同时物模试验通过压力传感器也测定出各断面在试验工况下不同位置的波浪力数据，具体的测点位置见图2；试验工况为水位3.60 m，水深5.80 m，波高3.76 m，波长65.5 m，周期9.1 s；波浪力数据见图3(测点处的压力方向为沿着测点所在的面法向，其中指向潜堤为正向，下同)。

图2 潜导堤断面压力监测点位置

图3 波浪力分布包络图(单位：kPa)

2 数值模型构建与验证

2.1 数值模型建立

基于Navier-Stokes方程和黏性不可压缩气液两相流理论建立二维数值水槽，方程求解采用的是压力与速度耦合求解算法中的PISO算法，物理模型选用多相流模型，湍流模型选用标准k-ε模型，自由液面模拟采用VOF追踪流体自由表面。

波浪数值水槽根据其功能具体划分为4个区间：60 m数值造波区、80 m消除建筑物边界二次反射的前端消波区、260 m模拟波浪与潜堤相互作用的工作区以及100 m消除末端边界反射的尾端消波区。数值水槽总长度取500 m。数值水槽模型的边界具体分为4种：对称边界、压力进口边界、壁面边界及内部边界。该数值水槽的左边界为对称边界；上边界为压力入口边界；结构物的外轮廓、水槽的下边界及右端边界为壁面边界；数值水槽中的各个功能区之间的界面为内部边界。波浪数值水槽结构见图4。

图4 波浪数值水槽结构(单位：m)

不仅如此，网格划分的大小也直接影响数模计算的稳定性和结果的精度，因此本次数值模拟为减小网格质量较差带来的计算误差，在水平方向上划分网格时，其网格划分密度达到一定的试验要求；在垂直方向上划分网格时，考虑到自由液面处是水质点运动的集中区域，为更好地捕捉自由液面区域的波面变化，对自由液面波高范围内的网格也进行了加密处理；同时为减小计算机的计算负担，对数值水槽顶部和底部的部分网格进行适当的疏松处理，整个数值水槽模型横向网格间距取0.8 m，竖向疏松部分间距取0.8 m，加密部分间距取0.25 m，全局水槽最小网格面积为0.2 m2，最大值为0.64 m2；而且为了使数值水槽底部和后续研究的建筑物边界处的黏度和速度梯度计算良好，在模型对其边壁做边界层处理(设置4层，层厚0.25 m)，具体处理后的网格见图5。

图5 波浪数值水槽网格

在此基础上，将操作条件设置为一个标准大气压，即101.325 kPa，并考虑重力作用，加速度方向沿y轴负向，值为-9.81 m/s2,设置工作流体为主相流体空气，密度设置为1.225 kg/m3，在对数值计算过程中控制系数等进行设置后，通过UDF文件导入对应的源项造波程序进行数值模拟计算。

2.2 数值波浪特征验证

本次模拟验证在8 m水深的条件下，以波要素(波高H=1.37 m，波周期T=9.1 s，波长L=39.9 m，规则波)为准，对水槽工作区内的工程位置处的波形和波要素进行对比验证，如图6所示。

由图6可看出，通过数值水槽模拟出来的波面比较规整，未发生破碎或者波形不一致情况，效果较好；波形能较快达到稳定状态，波浪的周期性也符合实际规律，重复性较好。

图6 工程位置处自由面模拟值与理论值对比

根据上述针对波浪周期性、重复性及稳定性特征的对比验证结果来看，数值水槽模拟出的波浪能够满足相应的波浪特征要求，在此基础上，可利用其开展波要素的数值模拟验证。

2.3 数值波要素验证

在已验证波浪特征的数值水槽基础上，分别建立潜导堤断面在4.83、3.60、2.10 m水位下的的波浪数值水槽模型，在实际工程的设计波要素条件下进行数值波浪模拟试验，然后将模拟出的波要素结果与设计值进行对比分析，从而实现实际工程设计波要素的模拟验证。不同水深对应波高与周期具体的数据对比见表2。

表2 波要素数值模型计算值与设计值对比

通过波要素数模计算值与设计值发现，两者的误差较小，波高及周期误差控制在5%以内，因此可利用该波浪数值水槽进行潜导堤断面波浪力的数值模拟验证。

2.4 数值波浪力验证

本次验证通过模拟实际工况，计算出波浪力数值结果，并将其与物理模型试验结果比较分析，得出验证结论。由于无论是在物理模型试验还是数值模拟时，潜导堤断面内坡(背浪面)处所受的波浪力相对外坡(迎浪面)和堤顶面都较小，且相对来说，正向波浪力要比负向波浪力大得多，因此本次潜堤波浪力数值模拟试验中各研究断面的测点主要用来测定在迎浪面和堤顶面位置处的正向波浪力；同时考虑到潜导堤断面外坡和顶面护面块体结构形式、尺寸、位置及潜堤堤身高度的特点，故在潜导堤断面外坡的护面块体上设置2个测点，堤顶面上设置3个测点，具体的测点位置见图5(测点处的压力方向为沿着测点所在的面法向，其中指向潜堤为正向，下同)，验证工况为水位3.60 m(水深5.80 m)、H1%=3.76 m、L=65.5 m、T=9.1 s。为了保证数值计算与物模试验中潜导堤结构特点的一致性，在数值模型中考虑四脚空心方块受力断面透空的结构特点，对护面块体结构进行了部分简化，这样既能维持其几何结构特点，也能对其透空作用进行等效模拟，具体断面见图7。

图7 波浪数值水槽试验断面

由图7可知，在数值波浪水槽中，波浪在越过潜堤时出现了破碎现象，由此可知数值水槽也能对波浪与结构物作用的现象进行模拟计算。

潜导堤波浪力数值计算结果与物理模型试验结果对比见表3。

表3 波浪力物理模型试验与数值计算结果对比

结合表3可见，正向波浪力数值计算结果与物理模型实测结果接近，误差基本能控制在6%以内；波浪力的分布规律也基本一致。这说明本文所运用的数值模拟方法能相对准确地计算潜堤波浪力，在此基础上可利用其进行实际阶梯型潜导堤工程的波浪力特性计算研究。

3 波浪力数值计算与分析

3.1 计算参数设置

本文主要研究淹没水深、波高对潜导堤波浪力的影响。因此依据1.2节中设计规则波波要素、设计水位的范围，并结合本文的研究目的，试验工况可按照水深及波高进行合理组合，进行数值计算，从而研究其具体的波浪力特性。

实际工况组合情况为：试验工况由8个水位、8个波长及8个波高条件进行相关组合，共41个工况，具体的计算工况组合及参数选取见表4。

表4 数值模型试验工况

续表4

工况水位∕m水深d∕m波长L∕m波高H∕m相对波高H∕d淹没水深dw∕m相对淹没水深dw∕d周期T∕s243.65.80.3721.60.276253.15.30.4081.10.208262.64.850.32.160.4500.60.1259.1272.14.30.5020.10.023281.63.80.568-0.4-0.105291.13.30.655-0.9-0.273303.65.80.3161.60.276313.15.30.3451.10.208322.64.846.61.830.3810.60.1259.1332.14.30.4260.10.023341.63.80.482-0.4-0.105351.13.30.555-0.9-0.273363.65.80.2791.60.276373.15.30.3061.10.208382.64.844.11.620.3380.60.1259.1392.14.30.3770.10.023401.63.80.426-0.4-0.105411.13.30.491-0.9-0.273

注：斜坡型潜导堤底高程-2.2 m，堤顶高程2.0 m。

3.2 相对波高与相对淹没水深对潜导堤波浪力的影响分析

根据数值计算的结果，对波浪力p进行无量纲化，得到无量纲波浪力p/(ρgL)，其中ρ为水密度(t/m3)、L为波长。经对试验数据进行整理后，得到无因次波浪力p/(ρgL)与相对波高H/d和相对淹没水深dw/d的关系，见图8、9。

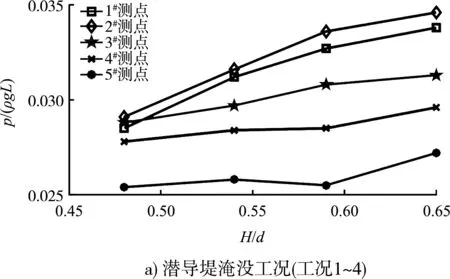
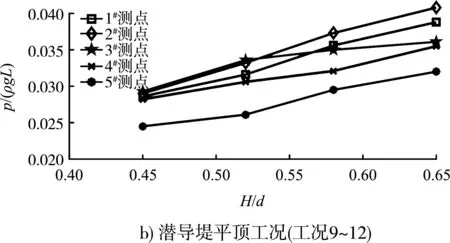
图8 潜导堤无量纲波浪力与相对波高关系

图9 潜导堤无量纲波浪力与相对淹没水深关系

由图8可看出，在控制水深、波长及周期保持不变的情况下，无论各潜导堤处于淹没状态或是出水状态，其迎浪面和堤顶面上的波浪力随着入射波波高的增大发生不同程度的增大；在相对波高H/d在0.43～0.65的变化范围内，波浪力均随着相对波高的增大而增大。这主要是因为入射波波高越大，其所储藏的能量越大，因此在破碎时对潜导堤的冲击也就越大。当潜导堤处于淹没状态时，迎浪面各测点波浪力随波高的变化相对于堤顶测点来说幅度更大，迎浪面对于波高变化更为敏感；当潜导堤处于平顶或是出水状态时，迎浪面与堤顶各测点波浪力随波高的变化幅度较为均匀，两者对于波高的敏感度基本一致。由此看出其迎浪面和堤顶面上波浪力对波高的敏感度与淹没水深有关。

由图9可看出，斜坡型潜导堤迎浪面与堤顶面波浪力随相对淹没水深的变化规律也比较一致，在相对淹没水深dw/d在-0.273～0.276的变化范围内，波浪力均随着相对淹没水深的减小发生先增大再减小。在相对淹没水深dw/d取0.125时(淹没水深为0.6 m)，堤顶面上的波浪力取得最大值；在相对淹没水深dw/d为-0.105时(淹没水深为-0.4 m)，迎浪面上的波浪力取得最大值。

在控制波要素保持不变的情况下，当潜导堤的淹没水深dw> -0.4 m时，迎浪面所受波浪力随着潜堤水深的减小而增大，当潜导堤的淹没水深dw≤-0.4 m，迎浪面波浪力随着水位的降低，波浪力逐渐减小；在控制波高、波长及周期等要素保持不变的情况下，当潜导堤的淹没水深dw> 0.6 m时，迎浪面所受波浪力随着潜堤水深的减小而增大；当潜导堤的淹没水深dw≤0.6 m，迎浪面波浪力随着水位的降低，波浪力逐渐减小。

随着水位的降低，迎浪面侧波浪力逐渐超过堤顶侧波浪力，在潜导堤出水时(淹没水深< 0 m)，这一现象最为明显，这主要是由于随着水位的降低，波高水深比值加大且不断趋于破波比，使波浪更易于在潜导堤前发生破碎，导致波浪的主要冲击集中在迎浪面上，形成较大的冲击力，然后一部分波浪向堤顶及背坡继续传播，由于能量的损耗而导致堤顶面的波浪力明显减小；且随着水位不断降低，入射波越来越难以越过潜导堤，因此堤顶位置所受的波浪力逐渐大幅减小，不断趋于0。

3.3 堤顶面最大波浪力计算公式

根据前人的经验计算公式，多以相对波高和相对淹没水深等来反映其与相对潜堤波浪力之间的关系。该斜坡型潜堤堤顶面最大波浪力的计算公式也可借鉴相关经验，但考虑到潜堤断面形式的差异，在相应的系数上又有所不同。

通过对试验数据的整理和多项式拟合分析，得到了各研究断面潜导堤堤顶面最大波浪力计算公式，表现为关于相对淹没水深的分段函数，具体如下：

(1)

此计算公式对应的相对淹没水深取值可适当放宽。

通过考虑该类波浪力公式的参数主要为相对波高和相对淹没水深，且这两个参数均为一次线性的形式，因此根据公式中相关系数取值可看出：对这两个参数来看，潜导堤波浪力对相对淹没水深的变化更为敏感。

为了验证本文潜堤堤顶面最大波浪力计算拟合公式的精确度，将公式计算值与数值模型试验值进行对比，见图10。

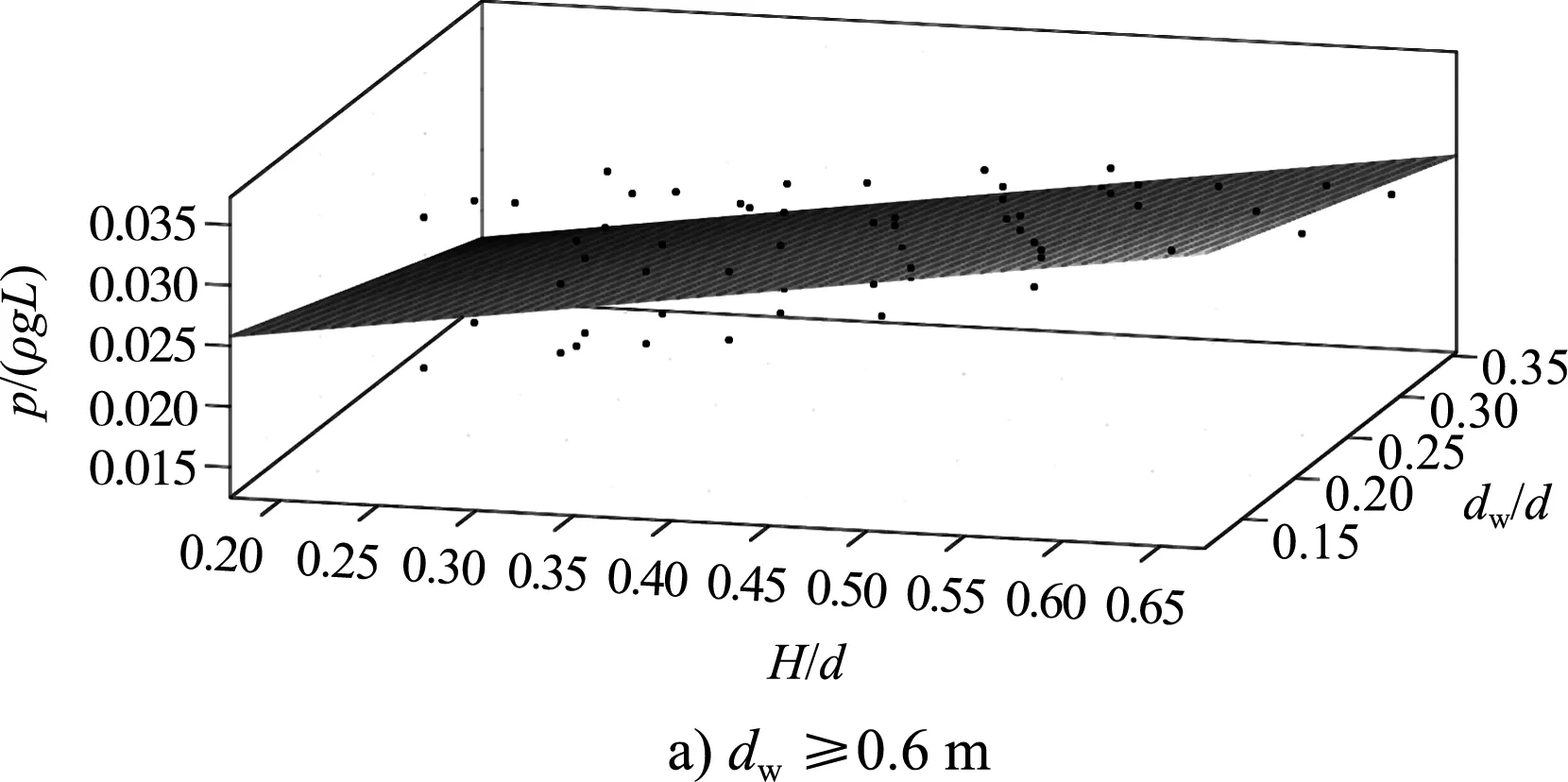
注：平面为波浪力计算公式所表示的平面，散点为数值模拟结果。

图10波浪力公式计算值与模拟值对比

比较图10的平面与散点位置可看出，此公式的拟合情况相对较好，根据式(2)～(4)计算得出其均方根RMSE≤3.4‰、和方差SSE≤0.67‰，确定系数Rsquare约为0.92，可为规则波作用下类似斜坡型潜导堤波浪力的计算提供相应依据。

(2)

(3)

(4)

式中：SSE为预测数据和原始数据的和方差；pi预、pi原分别为预测数据和原始数据；SSR为预测数据与原始数据均值的和方差；n为数据组数。

4 结语

1)在水位、波长、周期等因素保持不变的情况下，斜坡型潜导堤迎浪面与堤顶面波浪力均随着波高的增大而增大，且迎浪面和堤顶面上波浪力对波高的敏感度与淹没水深有关。

2)斜坡型潜导堤迎浪面与堤顶面波浪力相对淹没水深dw/d在-0.273～0.276的变化范围内，波浪力均随着相对淹没水深的减小先增大再减小。在相对淹没水深dw/d取-0.105时(淹没水深为-0.4 m)，迎浪面上的波浪力取得最大值；在相对淹没水深dw/d取0.125时(淹没水深为0.6 m)，堤顶面上的波浪力取得最大值。

3)随着水位的降低，入射波越来越早破碎，越来越难以越过潜导堤，堤顶位置所受的波浪力逐渐趋于0，迎浪面侧波浪力逐渐超过堤顶侧波浪力，且差值不断增大。

4)经对试验数据的整理和多项式拟合分析及验证，拟合出潜导堤堤顶面最大波浪力计算公式，适用于类似条件下工程设计水位和波要素组合工况下潜导堤上的波浪力的计算研究，为相应的实际工程断面设计提供理论依据。