星座备份策略研究进展

王许煜，胡敏，赵玉龙，徐家辉

航天工程大学，北京 101400

近年来，随着卫星技术的快速发展，各国对导航和通信等领域的需求也日益增长。然而，为了实现在全球或特定区域内提供连续、稳定的服务，仅依靠单颗卫星远远无法满足，这就需要利用多颗卫星协同工作，以完成任务。卫星星座由多颗卫星组成，各卫星之间通过协同控制在空间中保持相对稳定的几何构型，并利用多方位的信息互联，从而实现对目标区域连续的多重覆盖和性能保证。星座由于其巨大的发展潜力，尤其是在军事应用中无可比拟的优势，受到了各国越来越广泛的关注，呈现迅猛发展的态势。

作为一个复杂的空间系统，星座的运行管理面临许多挑战。星座卫星在轨运行过程中，为了消除摄动力对卫星运行轨道的影响，需要对卫星进行轨道机动以保持其轨道。此外，由于受到卫星自身寿命和可靠性的限制，以及复杂恶劣的太空环境的影响，卫星会出现短期故障(可恢复的故障)或长期故障(不可恢复的故障)[1]。所以，为了保证星座系统一直处于连续且稳定的运行状态，需要根据其实际状况采取不同的备份策略。星座备份策略的选取会对星座系统的可用性、连续性和完好性产生直接影响，是星座系统设计的一项重要内容。当卫星发射或运行发生故障时，星座备份是确保星座系统成功组网和稳定运行的关键因素[2]。

在星座备份策略研究中，替换策略的优化至关重要。当前，有关替换策略优化的研究主要集中在系统部组件层次，文献[3]开创性地引入多个单一单元模型，为后续替换策略优化研究奠定了基础。文献[4-6]综述了20世纪50年代初～80年代末有关替换策略优化和模型的发展与应用情况。文献[7]在此基础上对该问题进行进一步的总结，认为对于研究相对较少的多单元模型，状态空间维数问题可能是限制其发展的原因。而由于星座系统的复杂性，关于星座建模及其备份策略的研究则相对较少。

本文归纳总结了3种不同的星座备份策略模式(即在轨备份、停泊轨道备份及地面备份)及其特点。然后，梳理了国内外星座备份策略关键因素的研究进展。接着，对目前星座备份策略分析的主要模型和方法进行综述。最后，展望了星座备份策略研究的发展方向。

1 全球主要星座备份现状分析

1.1 导航星座备份现状分析

备份与替换策略一直是GPS星座研究的重要课题。GPS星座最初的设计是由24颗卫星组成，但为了满足星座中有24颗卫星可以投入运行的概率达到95%[8]，自1993年满星座运行以来，实际的运行卫星数量一直保持在27颗以上[2,9-10]。GPS星座采取的在轨备份策略是在星座中具有较高故障率的卫星附近部署一颗备份卫星，从而形成一对卫星协同工作，一旦工作卫星出现故障，备份卫星可以经过一次或两次的轨道机动完成对故障卫星的快速更换[11]。同时GPS还采取了地面备份的策略[12]，在地面上始终有大量等待替换的备份卫星，构成多重备份。

总体来看，GPS在星座组网和运行阶段均考虑了星座备份以确保发射和运行稳定，由于大部分卫星均超期服役，使GPS在星座维持上具有相当大的灵活性，并在一定程度上节省了经费。目前GPS系统在轨卫星32颗，其中31颗卫星处于运行阶段，1颗卫星处于维修阶段。GPS星座空间构型如图1所示。

图1 GPS星座空间构型Fig.1 GPS constellation space configuration

与GPS星座相比，俄罗斯GLONASS星座由于卫星可靠性差，寿命短，导致星座备份维持成本极为高昂。目前GLONASS星座在轨27颗卫星，其中22颗卫星处于正常工作状态，2颗处于维修状态，1颗处于飞行测试阶段，同时还有2颗在轨备份卫星。GLONASS星座的备份卫星位于同一个轨道面上，且都停止播发导航信号，处于冷备份状态。当星座中的工作卫星发生故障时，才启动备份卫星[2]。

表1给出了GLONASS星座备份情况，其中备份卫星COSMOS 2424和COSMOS 2436与其轨道面中最近的在轨运行卫星COSMOS 2522和COSMOS 2534的相位差分别为2.864°和5.842°。

表1 GLONASS星座备份情况

Galileo星座在考虑星座备份时借鉴了GPS的经验，在设计阶段详细研究了星座组网与可靠运行问题。Galileo星座采用3个倾角为56°的轨道面组成的Walker星座，由27颗运行卫星组成，采取在每个轨道面上部署一颗备份卫星的策略。与GLONASS星座一样，Galileo星座的备份卫星也处于冷备份状态，当工作卫星发生故障时，备份卫星通过移动来更换故障卫星，从而快速修复星座中的故障，而不需要等待安排新的卫星发射[13]。

综上分析，现有导航星座GPS、GLONASS以及Galileo采取的星座备份策略如表2所示。

表2 导航星座备份策略

1.2 通信星座备份现状分析

在商业通信星座中，通过按需发射来替换故障卫星，这可能会导致无法接受的延迟[14]，所以通信星座一般采用在轨备份或停泊轨道备份和地面备份相结合的模式。

第一代Iridium星座由6个倾角为86.4°的轨道面组成，每个轨道面上部署11个工作卫星以及1个备份卫星，其中工作卫星轨道高度为780 km，备份卫星轨道高度为648 km，略低于工作卫星轨道高度[15]。由于第一代Iridium星座的老化和升级，2019年1月铱星公司与SpaceX完成了第二代Iridium星座75颗卫星的部署，包括66颗在轨工作卫星和9颗备份卫星，同时还有6颗地面备份卫星。

GlobalStar第一代星座由48颗工作卫星和8颗备份卫星组成，工作卫星均匀部署在8个倾角为52°，高度为1 414 km的圆形轨道上，同时在每个轨道面部署1颗备份卫星，备份卫星的轨道高度为900 km，低于星座的运行轨道[16]。Globalstar星座自2016年2月全面部署以来，目前共有32颗运行卫星，包括8颗第一代卫星和24颗第二代新卫星，旨在提高星座的覆盖范围和可靠性[17]。

为了提供宽带服务，OneWeb计划生产900颗卫星，在低地球轨道(LEO)建立一个大型卫星星座，星座共有648颗卫星部署在18个高度为1 200 km，倾角为87.9°的轨道平面上，其中有600颗工作卫星以及48颗在轨备份卫星，其余卫星将用作地面备份。

SpaceX正在规划一个由近1.2万颗相互连接的宽带互联网卫星组成的巨型星座(Starlink)，该星座具有两个子星座。第一个子星座由4 425颗卫星(包括备份星)组成，卫星分布在83个不同高度和不同倾角的轨道面上，轨道高度1 110～1 325 km，轨道倾角53°～81°，同时计划在每个轨道面部署两颗备份星，以便在卫星故障时补充星座。如果工作卫星没有发生故障，则备份星将处于休眠状态，即冷备份，并将与其他活动卫星一起保持星座构型以及规避碎片碰撞的操作。第二个子星座共有7 518颗卫星，部署在3个不同高度和不同倾角的轨道面上，轨道高度分别为345.6 km、340.8 km和335.9 km，轨道倾角分别为53°、48°和42°[18]。

2 星座备份策略模式

备份策略是指为了防止因工作卫星发生故障而导致星座无法满足所需性能要求时，采取的星座冗余配置设计[19]。为了提供长期服务，星座必须考虑到更换个别卫星的需要[20]。备份策略通常包括3种模式：在轨备份、停泊轨道备份以及地面备份，前面两种统称为空间备份[11]。由于空间备份模式具有平均修复时间较小的优势, 在星座系统备份中得到了广泛的应用[21]。

2.1 在轨备份模式分析

在轨备份模式是将备份卫星部署在与星座标称轨道相同的高度上，每个轨道面一般需要放置至少一颗备份卫星，但是这种备份方法需要较多的卫星，具有较高的成本。当星座中的工作卫星发生故障时，备份卫星将通过相位调整，分阶段到达所需的位置，从而对故障卫星进行快速替换，只要合理使用燃料，故障卫星在几天内就可以完成更换。在轨备份模式由于具有快速替换故障卫星的优点，所以是星座备份中最常用的一种模式。

在轨备份的另一种形式是激活备份卫星并将其作为星座的一部分使用[22]，以达到冗余备份的目的，从而有效增强星座的服务性能，使其处于最佳运行状态，同时提高星座的鲁棒性，减少故障快速替换的需求[23]。然而，冗余备份模式一旦发生故障，星座内的许多卫星可能不得不通过重新发射新卫星的方式来替换。冗余备份模式通常包括以下两种方式：

1)单星备份。在达到服务性能要求的星座标称构型上，给每个轨道面额外部署一颗备份星。倘若星座中的工作卫星出现故障无法提供服务，由于备份卫星处于工作状态，所以不需要调整备份卫星的轨道相位就可以满足服务性能的最低要求，同时也给予备份卫星充分的重构时间。

2)双星备份。对于具有非常高可用性需求(99.9%甚至更高)的星座，采取在每个轨道面上部署两颗备份卫星的双星备份将会是一种更好的选择[24]，这不仅可以提高星座备份的效率，缩短备份时间，同时在服务性能增强方面也具有积极的作用[25]。除非卫星遭受打击，否则在同一轨道面上很难出现3颗或更多的卫星同时发生故障的情况[26]，所以，通常不考虑备份3颗卫星的方式。

2.2 停泊轨道备份模式分析

停泊轨道备份是将备份卫星部署在低于星座轨道高度的停泊轨道上。由于轨道高度差的存在以及摄动力引起的相对相位角变化，停泊轨道面会相对星座轨道面不断漂移，在停泊轨道漂移的过程中，备份卫星可以根据实际情况对不同的轨道面进行故障卫星替换，所以一般会在停泊轨道上部署多颗备份卫星。当备份卫星轨道面调整至与星座轨道面重合时，备份卫星通过提升轨道高度，然后进行相位调整，分阶段到达星座轨道上所需的位置，这样可以消耗较少的燃料。然而，停泊轨道备份模式利用轨道漂移来调整备份星轨道面需要较长时间，特别是对于在近地轨道(LEO)的应用，如果轨道高度差异很小，则相对相位角变化速率也很小。所以，采用这种备份模式替换一颗故障卫星的时间通常约为1～2个月[22]。

文献[24]从轨道高度和轨道倾角两个方面讨论了备份卫星停泊轨道的设计，综合考虑了卫星控制速度、故障卫星平均修复时间以及备份星数目等因素，得到停泊轨道模型。通过分析，笔者认为在一定的轨道倾角容许漂移量内，备份卫星只需要在备份轨道内通过相位调整即可实现快速替换故障卫星，但与此同时也要综合考虑调整轨道面的一致性所消耗的燃料。

相较于在轨备份模式，由于卫星替换时间较长，停泊轨道备份的备份效率较低。同时，部署在停泊轨道上的备份卫星一般都处于冷备份状态，所以该备份模式达不到增强星座性能的效果。综合上述原因，对于可靠性和可用性要求非常高的导航星座来说，这种备份模式并不适用。然而，如果星座对可用性的要求小于95%，则可以首先选择停泊轨道备份模式[27]，如Iridium星座、GlobalStar星座等通信星座一般都会采用停泊轨道备份模式。

星座采用停泊轨道备份模式需要综合考虑以下因素[28]：备份卫星通过轨道机动从停泊轨道转移到星座轨道所需的ΔV，备份卫星在星座轨道内调整相位并重新定位所需的ΔV以及卫星故障与星座服务性能恢复之间的时间延迟。

2.3 地面备份模式分析

地面备份模式是将备份卫星存储在地面上，如果星座中的工作卫星发生故障，则立即发射备份卫星以替换失效卫星。这种模式的好处是备用卫星可用于测试和改进，直至发射时为止，同时只需在地面存放少量的备份星即可达到备份的目的。然而，由于这种备份方式发射周期长，所以需要很长的时间才能实现对故障卫星的替换，一般都需要数月或者一年甚至更长的时间[29]。地面备份方式可能因为备份星发射延迟而导致星座长时间服务中断，所以这种备份模式一般只适用于对可靠性和可用性要求不高的星座。

2.4 星座备份策略模式比较

从维持星座性能的角度看，最佳的备份模式始终是在轨备份，然而，根据星座的性能要求，在轨备份可能需要备份多颗卫星以提供更高的服务性能。特别是对于具有多个轨道面的星座，若每个轨道面至少部署一颗备份星，则需要制造和发射许多额外的卫星，导致较高的备份成本。

在停泊轨道备份模式中，一颗备份星可以对不同轨道面进行备份，如果有较多的停泊轨道，尽管轨道漂移速度慢，但仍然可以在一定程度上缩短替换故障卫星的时间。然而随着停泊轨道的增多，需要制造和发射更多的备份星，同样会提高成本。

当星座对服务性能要求不高时，则可以采用地面备份模式。由于所需备份卫星较少，从长远来看，相比于其他两种备份，地面备份具有最低的备份成本。但该模式替换故障卫星所需的时间最多。所以这种模式通常作为前两种模式的后备模式，与前两种模式结合使用。表3给出了3种备份模式的对比。

表3 星座备份策略模式对比

3 星座备份策略的关键因素

星座备份策略的研究受到许多因素的影响，包括星座运行中的各种确定性因素和随机因素。针对现阶段星座备份策略的主要模式与星座服务性能需求，本节重点论述星座备份策略中卫星故障模式、卫星可靠性、卫星可用性、星座状态概率和星座系统可用性等5项关键因素。

3.1 卫星故障模式分析

在星座运行的过程中，由于受到空间环境和自身组件损耗的影响，星座中的卫星会发生故障，从而改变星座的运行状态，影响星座的服务性能。因此必须确定星座的运行管理计划，降低星座寿命周期内卫星故障的影响，以避免严重的服务中断[30]。卫星故障可以分为以下几种类型[31]：

1)长期故障：卫星中的单个或多个组件发生故障，且不可通过在轨维修或使用星载备份进行修复，从而导致卫星不再正常工作。一旦发生长期故障，若不及时使用备份卫星，会对星座的服务性能造成极大的影响。

2)短期故障：卫星发生故障后会暂时停止工作，通过及时的在轨维修或者使用备份组件对故障组件进行替换，可以在几小时或几天内恢复功能。短期故障由于其可恢复性，对星座的服务性能影响是有限的，所以并不需要使用在轨备份星或发射新卫星进行替换。

3)维护故障：为了保持星座空间构型或提高卫星性能，会对星座进行维护操作，在此期间所导致的卫星停止提供服务，虽然也会降低星座的服务性能，但通常不认定其为“故障”。由于星座一般都具有预先制定的维护计划，所以并不会因此导致服务的中断，仍然具有连续性。

为了更好地描述卫星运行期间的各类故障，一般都使用以下参数[25]：

1)平均故障间隔时间(Mean Time Between Failure，MTBF)：对于长期故障，由于卫星发生故障即永久失效，该参数一般指卫星实际运行寿命的平均值；而对于短期故障，该参数一般用来度量卫星相邻故障之间的时间间隔的平均值。

2)平均维护间隔时间(Mean Time Between Maintenance，MTBM)：指星座进行维护操作的平均时间间隔。

3)平均修复时间(Mean Time To Replace，MTTR)：对于长期故障，该参数是指备份卫星替换故障卫星并进行正常工作所需要的平均时间；而对于短期故障和维护故障，一般是指修复短期故障以及维护操作所需的平均时间。

3.2 卫星可靠性建模分析

可靠性的定义为在特定的条件和时间下，产品能完成指定任务的能力[32]。卫星系统可靠度一般根据设备或分系统可靠性预计值利用系统可靠性模型计算得到[33]。卫星可靠性的提高，不仅可以保证维持星座正常布局和运行的可用卫星数量，而且可以降低卫星的中断频率，从而减少备份卫星发射的次数和成本[34]。但是，仅仅依靠增加单颗卫星的可靠性来满足所需的星座可用性, 将需要采用大量的冗余度设计，包括增加卫星零部件备份或者在星座系统中部署更多的备份星，会直接导致卫星研发、制造以及发射费用的增加[35]。

传统的卫星可靠性模型一般都采用指数模型，Ochieng 等[36]通过假设卫星的故障概率密度函数服从指数分布得到相应的寿命分布，最终得到卫星可靠性指数模型：

R(t)=e-λt

(1)

式中：λ为故障率，其数值为1/MTBF。

文献[12,37-38]中也都采用了指数模型来描述卫星可靠性，然而传统的卫星可靠性模型虽然有利于简化和分析问题，但假设故障率是常数，不能准确地描述卫星早期故障、损耗累积和老化的过程。通常，由于早期故障期，在卫星早期的运行中具有较高的故障率，然后随着卫星零部件开始损耗，故障率在卫星生命末期会迅速增加[39]。

文献[40]介绍了用于星座可靠性和可用性分析的软件(Operational Constellation Availability and Reliability Simulation，OSCARS)，在OSCARS中卫星可靠性模型可以通过单个概率分布或者通过不同的概率分布来表示卫星各个寿命阶段(早期故障期、工作寿命期和损耗期)来建立。早期故障期可利用用户指定的概率分布进行建模。利用Weibull分布可以建立卫星工作寿命期可靠性模型，同时该文献指出，Weibull分布经常被用于模拟卫星故障。损耗期有4种不同的建模方法，第一种方法被描述为一个固定的截止日期，即卫星故障要么发生在指定日期之前，要么发生在指定日期，其他方法包括瑞利分布、正态分布和具有固定截止日期的正态分布。

文献[41]通过研究卫星子系统对卫星可靠性进行分析建模，通过将一个指数分布和一个有3个参数的Weibull分布进行线性组合，提出了一个具有5个参数的故障概率密度函数，其中指数分布用来模拟一个组件的初期故障期，Weibull分布用来模拟组件的剩余寿命。该文献指出，利用这个概率密度函数进行可靠性建模考虑了组件的实际情况，可以替代组件寿命的指数模型。组件的故障概率密度函数可以写为：

f(x)=PIMfIM(x)+(1-PIM)fW(x)

(2)

其中：

式中：fIM(x)表示指数分布；fW(x)表示Weibull分布；PIM为早期故障概率；θIM为早期故障期的预期寿命；δ为最短寿命期；θ为比例参数；β为形状参数。

文献[42]借鉴了GPS星座的经验，考虑了随机故障和损耗故障，建立了更为准确的卫星可靠性模型：

(3)

式中：α为尺度参数；μ为均值；σ为标准差；t为卫星的使用时间。

文献[42]分析了卫星在整个寿命周期内的可靠性变化，并与指数模型进行了比较。从图2中可以看出，与传统的指数模型相比，改进模型在卫星寿命期内可靠性比较稳定，超出设计寿命后可靠性急剧下降，这与卫星的实际状态更为符合，更能描述卫星在整个寿命周期内可靠性随时间变化的真实状况。

图2 卫星的两种可靠性模型对比情况Fig.2 Comparison of two reliability models of satellites

卫星可靠性模型的准确性关系到卫星末期可靠性和卫星剩余寿命的预测，从而影响星座备份策略的最终选取。表4给出了4种卫星可靠性建模方法的对比。

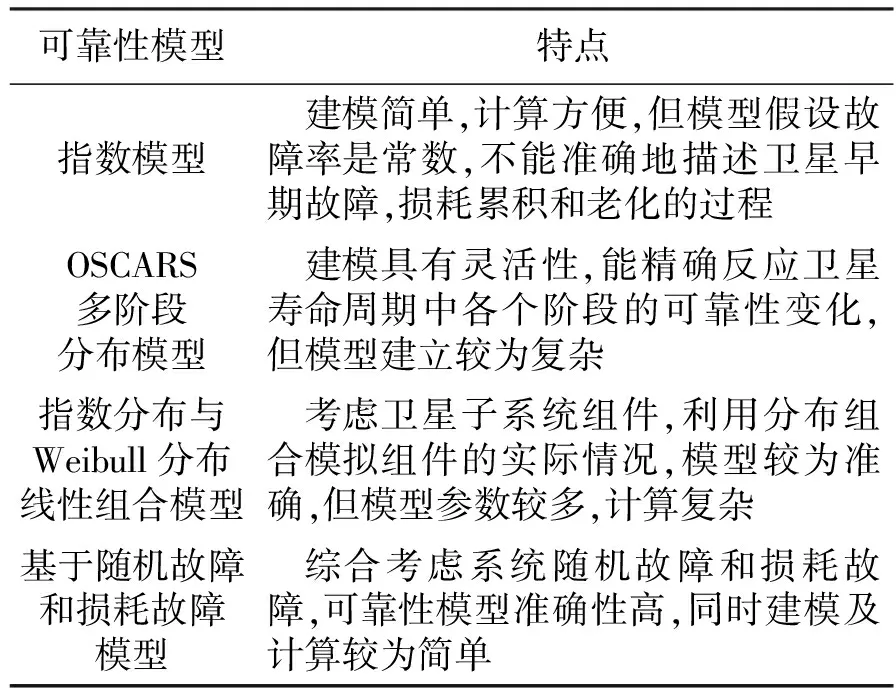
表4 卫星可靠性建模方法比较

3.3 卫星可用性研究分析

可靠性研究只考虑了单个卫星的故障率，并没有综合考虑卫星在轨修复或按需替换的特性，而可用性则用于表示卫星处于工作状态的程度，是卫星可靠性和可维护性的综合反映。卫星不同的故障模式所导致的服务中断是影响卫星可用性的一个直接因素。

文献[43]首先给出了单颗卫星可用性的计算方法，并在此基础上分析了卫星处于长期故障和短期故障模式下的卫星故障率。由于长期故障和短期故障的不同特性，作者讨论了短期故障下的卫星修复率，并综合考虑星座在轨备份和地面备份策略，给出了长期故障下的卫星修复率，最终得到等效的卫星故障率λ和卫星修复率μ。

文献[25]同样基于卫星不同的故障模式以及星座备份策略，利用马尔可夫状态转移模型对单颗卫星进行了分析，最终得到卫星的稳态可用性。然而与文献[43]不同的是，作者还考虑了维护操作所引起的故障对卫星可用性的影响。同时文章还利用文献数据进行了实验分析。实验结果表明，当平均故障间隔时间增加，处于长期故障模式下的卫星可用性提高最为显著。通过对3种故障模式进行比较，可以得出卫星可用性最容易受长期故障模式的影响，而受维护故障模式的影响则最小。所以提高卫星处于长期故障模式下的平均故障间隔时间，对可用性的提高有着十分积极的作用。

文献[19]针对卫星星载组件寿命周期和故障恢复时间服从以及不严格服从指数分布的情况，分别对卫星可用性进行建模分析。对于服从指数分布的情况，作者利用连续时间马尔可夫链(Continuous Time Markov Chain，CTMC)模型，并基于 Laplace变换给出该模型的求解方法，从而得到卫星的瞬时可用性，进一步得到单颗卫星的稳态可用性。卫星可用性表示为:

(4)

式中：MTBF=1/λ；MTTR=1/μ。

而对于不严格服从指数分布的情况，则利用时齐半马尔可夫过程(Semi-Markov Process，SMP)模型。模型中使用统计抽样的方法对状态转移概率进行了估计，同时还进一步估算了转移参数并获得状态的分布矩阵，最终计算得到单颗卫星的瞬时可用性。

3.4 星座状态概率计算分析

文献[42]定义了在不同时刻下星座的所有可能状态，并根据卫星的可靠性计算出不同状态下的星座状态概率。由于各卫星的可靠性不同，所以不同故障卫星组合下的星座状态概率也不同，可得：

(5)

文献[42]虽然利用卫星的可靠性计算出了星座不同故障状态下的概率，但忽略了星座备份策略的影响。文献[25]则在不同卫星故障模式的基础上，采用时齐马尔可夫链模型，充分考虑了星座备份策略，通过假定星座系统的卫星故障率、修复率及状态转移时间间隔得到相应的状态转移矩阵，然后根据星座状态的初始条件求得在相应时间间隔后星座处于不同状态的概率。马尔可夫链是一种常用的星座状态概率估计工具，在文献[44-45]中，作者同样都采用了马尔可夫链对星座状态概率进行建模分析。

3.5 星座系统可用性模型分析

星座系统通常选择服务可用性作为其性能指标，主要指卫星提供的服务在目标区域内能满足用户需求的时间百分比[43]。星座系统可用性在实际应用中具有非常高的价值，通常是星座构型设计、分阶段部署和备份策略选择的主导因素之一[46]，其数值一般取决于星座状态和星座的几何构型。随着星座运行时间的推移，卫星可靠性会随之发生改变，一些卫星可能会因故障而停止工作，因此星座状态概率也在发生动态变化。与此同时，星座中故障卫星的出现会导致星座的几何构型发生改变，从而影响星座性能。因此，星座的可用性会随着运行时间的变化而变化[42]。可用性的优化是一项极其复杂的系统工程，需要投入足够的精力来做出决策[34]。

在一定的平均修复时间内，星座所达到的性能水平可以很好地反映整个星座生命周期内的可用性[47]。星座的服务可用性可以定义为星座状态概率和星座值相乘之和。在文献[40,48-49]中利用此定义给出了星座系统可用性模型：

(6)

式中：N为卫星数目；CVk(t)为t时刻下有k颗卫星故障时的星座值，反映星座的几何特征和连续可见性，是星座性能的重要表现。

在其他文献中，文献[34]研究分析了单颗卫星可靠性与星座可用性之间的关系，并利用蒙特卡洛方法对星座可用性进行模拟仿真。文献[50]基于马尔可夫过程给出了单颗卫星可用性算法，并利用星座状态概率对星座可用性进行了建模分析。

4 星座备份策略模型与方法研究

对星座进行备份能有效避免星座因卫星故障而发生严重的服务中断。在星座备份策略研究中，采用不同的模型与方法将直接影响星座备份策略的选取与优化，针对各模型与方法的特点及其适用解决的问题，本节重点综述目前星座备份策略分析的主要模型和方法，包括Petri网、马尔可夫链以及存储论。

4.1 Petri网模型和方法

文献[2]利用Petri网建立了具有多约束的星座运行状态变化模型，将星座在不同时刻所发生的事件当作Petri网模型的变迁，通过变迁来实现星座状态的动态变化。模型综合分析了星座运行过程中的确定性因素(如星座备份策略、星座运行逻辑)和不确定因素(如卫星故障时间、故障恢复时间)，并依据各事件发生的概率模拟仿真了星座系统的实际运行情况。最后作者利用蒙特卡洛方法分析了在不同备份策略下星座系统可用性的随机分布情况。

Ereau等[51]利用Petri网讨论了星座可用性问题。通过Petri网对星座进行建模，该模型通过一个由不同模型段的较小Petri网所组成的全局Petri网来实现。作者指出，与其他类型的模型相比，使用Petri网对卫星星座进行建模能够更好地处理星座状态数的组合爆炸，并且可以在不改变模型的情况下对输入参数进行广泛的敏感性分析。为了得到模型的定性结果，作者采用了蒙特卡罗仿真，同时指出，由于要用于问题的定量分析，Petri网必须拓展为包含时间的使用，即为随机赋时Petri网，但是为了合理地利用时间，分析结果仍将面临状态空间爆炸的问题。

Petri网作为一种既具有数学分析和仿真的能力，也有直观的图形表达能力的建模工具，可以详细地表达系统中的运行逻辑，反映系统的静态布局以及动态变化，目前已成为星座模型建立的主要工具之一。但当星座卫星数量增大时，Petri网模型将发生状态爆炸，从而提高了模型复杂度，导致计算量增大。

4.2 马尔可夫链模型和方法

文献[6]从分析的角度探讨了卫星最优替换策略的确定问题。作者采用离散时间马尔可夫决策过程进行建模，允许卫星星座在每个决策元处于有限数目的状态，并利用马尔可夫决策过程(随机动态规划)的标准策略评估算法，对系统在给定时间范围内进行评估，以确定最优的替换策略和最小的预期总成本。同时，还对模型参数进行敏感性分析，为评估最优值如何受到模型参数变化的影响提供了一种方法。在问题分析的过程中，作者对卫星及其运行进行了若干假设，如没有发射提前时间和只考虑地面备件，来限制Ereau和Saleman提出的星座状态爆炸问题，但这些假设是有局限性的。此外，特别是对于大型星座而言，星座状态数仍然非常多，例如，对于一个由9颗卫星组成的星座，其运行状态数就达4 680个。

Kelley等[52]也使用马尔可夫链模型来评估星座系统的寿命周期成本，包括卫星的获取、补给以及运行成本，并在成本和性能两个主要部分之间建立了适当的联系。作者还利用全局优化技术(模拟退火和遗传算法)对局部优化技术(单纯形和复形)的性能进行了评估，以提供星座覆盖的可用性，并通过比较发现遗传算法的全局优化性能略好于模拟退火算法。但是同样的，这种模型会随着星座规模的增大而导致星座状态爆炸，因此无法拓展到大型星座。

文献[53]首先给出了单个卫星形式规范及其相关的连续时间马尔可夫链模型，并在此基础上对星座系统进行建模分析。然后利用概率模型检查工具PRISM[54]对单个卫星和星座的可靠性、可用性和可维护性(RAM)进行了分析。系统的可靠性、可用性和可维护性分析在卫星的设计阶段必不可少，以便实现最小的故障或增加平均故障间隔时间，从而规划维护策略，优化可靠性和最大限度地提高可用性。

到目前为止，星座模型分析多采用马尔可夫链方法。马尔可夫链建模较为简单，可以得到系统的稳态特性，具有建模便利和求解快速的优点[2]。但是由于模型建立过程中对实际问题做出了过多的假设，具有局限性。同时与Petri网一样，随着星座中卫星数量的增多，会导致星座状态爆炸和计算效率下降。

4.3 存储论模型和方法

利用库存管理方法对卫星星座备份策略进行建模的文献较少。文献[55]从简单的卫星层面分析了卫星的补给问题，并使用经典的(N,M)库存系统解决了这个问题。模型考虑了星座系统中运行卫星的总数, 当卫星总数从M降到N时，就开始对星座进行补网发射，使系统卫星总数重新到达M。并利用卫星随时间发射的数量成本函数，推导出一种最优策略。然而，文献所提出的库存模型非常简单，并具有局限性：首先，卫星总数补给到M的过程中不允许一致的发射计划；其次，它不能反映卫星批量发射可以节省成本的真实性，也没有明确考虑停泊轨道的使用。这些局限性使得所提出的策略不适用于大型卫星星座。

文献[56]利用库存管理的方法，考虑了一组低于星座轨道高度的停泊轨道用于存储备份卫星，并利用多级(s,Q)库存策略对星座备份策略进行建模，提出了一种基于停泊轨道特性和所有位置政策的优化备份策略，然后在满足系统性能要求的前提下，对系统的维护总成本进行了优化设计。该模型将卫星星座备份策略看作一个多层次的备份供应链系统，旨在同时考虑系统中不同级别的备份卫星，将地面备份看作供应商，停泊轨道备份看作仓库，而在轨备份则看作零售商。在此基础上，模型假设了随机需求(故障)和备份交付时间，并通过拉丁超立方抽样仿真，对所提出的分析模型的精度进行了评估。作者强调了卫星通过批量发射来节省成本的重要性以及多个停泊轨道为所有轨道面提供备份所带来的灵活性，并说明了该多级混合策略对大型星座的价值。多级(s,Q)存储策略补给周期示意如图3所示，当库存中的存储水平下降到或低于s个可用单元时，将向其供应商发出数量为Q的订单。

图3 (s,Q)存储策略补给周期示意Fig3 Illustration of (s,Q)inventory policy replenishment cycles

利用存储论对星座备份问题进行建模可以有效解决由于星座卫星数目增大导致的星座状态爆炸的问题，同时该模型能提高星座备份策略的灵活性，为大型的导航、通信星座的备份问题提供了参考。但由于存储论综合考虑了不同星座备份策略的应用，使得星座模型的建立较为复杂。

5 总结和展望

星座备份策略研究涉及多个领域，具有多重的约束条件和性能指标，是极为复杂的工程问题。为了得到理论上最优的备份替换策略，必须对多个因素进行假设分析，这为该问题提供了更多的研究方向。星座备份问题可以在以下方面开展进一步的研究：

1)目前的卫星可靠性模型通常假设服从指数分布或几个分布的组合。然而，通过对卫星可靠性的分析，可得卫星具有早期故障这一问题。为了更准确地反映实际情况，需要观测在轨卫星以提供准确的故障数据，从而建立更为真实可靠的模型。

2)星座模型建立的过程中，为了简化问题假定卫星在轨状态为可操作或不可操作。然而对于单个卫星来说，当部分组件发生故障时，卫星仍可以处于运行状态。所以需要利用多个状态来表示卫星在不同时期的健康状况从而更准确的描述现实场景，并在退化状态下对卫星进行评估以确定合理的替换时间点。

3)对地面备份进行更深入的研究分析是模型的另一个拓展。由于在星座的运行过程中，需要在卫星预期故障之前订购备份卫星，这可能导致星座需要补网时无法及时获得备份卫星，或者在卫星发生故障之前为存储地面备份卫星而花费高额的费用，所以需要对替换订单的提前时间开展深入分析。另一方面，卫星存储在地面的过程中，卫星技术和设计的进步可以提升卫星的寿命和能力，但若对卫星进行改造将增加成本，所以需要对这种更为现实的因素开展综合分析。

4)在星座备份策略研究中，最佳替换策略的目标函数通常单一地考虑最低预期总成本、最佳服务性能或几何覆盖准则等因素。而如今对单一条件的满足已无法实现星座对不同任务的要求，必须在最优效率水平上进行权衡，这就需要对包含不同效率结果的代价目标函数开展计算研究。