折叠式变体飞行器轨迹优化及控制分析

杨博，朱一川，魏延明，樊子辰

1. 北京航空航天大学 宇航学院，北京 100191 2. 北京控制工程研究所，北京 100190

临近空间滑翔式高超声速飞行器是一种从亚轨道高度再入，不依靠发动机仅依靠空气动力控制实现远距离投送的飞行器。这种飞行器具有不受天气影响、隐身性能好、作战响应快速、战场生存能力强和射程较远等优点[1]。然而，临近空间瞬态的环境变化具有复杂性和随机性，在飞行器运行过程中，再入段会受到过载、热流率和动压的约束，而复杂的临近空间大气环境对高超声速有着巨大的影响，尤其是大气密度对飞行器气动特性的影响显著[2]。传统飞行器发展很快，但飞行模式单一，只能执行特定的任务，如飞机、导弹等。随着飞行器工作环境日益提升的复杂度，飞行器需具有更高的性能和更好的适应性。作为新一代飞行器的重要发展方向，变体飞行器能根据飞行环境和任务需求大尺度改变自身结构，以获得最优的气动布局和操作性。而目前很多飞行器既要追求超高音速性能，又要追求高机动性能，还要具有挂载能力，能够进行对地攻击，普通的飞行器无法满足复杂的飞行环境和飞行任务的要求，故而需要变体飞行器。

在变体飞行器航迹问题研究方面，Mujahid等通过在不同的飞行阶段切换不同的气动外形来实现飞行性能最优[3]；Thomas等针对折叠翼飞行器在缩放过程中引起的大面积和大弦长变化问题建立相应模型，结合多体动力学的分析方法，全面分析研究了在折叠翼飞行过程中飞行器基于飞行稳定性的轨道跟踪算法[4]；陈铁彪等研究优化了一种伸缩翼外形变体飞行器的轨迹并对其进行了性能分析[5]；袁亮研究优化了变体飞行器栖落机动的轨迹[6]；闫斌斌等通过增强学习的方法提供了一种变体飞行器自适应的变体策略[7]。但是变体飞行器利用变形改善飞行性能的同时，气动特性也发生了巨大的变化，从而导致对飞行器的控制难度增加[8]。张希彬等考虑了气动、推进、弹性耦合的高超声速飞行器的控制建模问题[9]；夏川等采用有限时间切换 H∞跟踪控制变体飞行器[10]；梁小辉等采用切换系统对变体飞行器进行控制[11]。然而，国内外对变体飞行器的研究基本都基于普通巡航的飞行器，相对速度低，而针对临近空间高超声速的飞行器鲜有研究。

本文将通过对临近空间滑翔式变体飞行器进行航迹优化，综合考虑射程以及热流率峰值的性能指标，根据仿真结果、折叠角以及气动姿态角进行控制。

1 折叠式可变形滑翔飞行器

为解决目前再入段飞行器的主要问题，本文提出一种机翼折叠的方法，折叠翼可以让飞行器在处于不同工作任务时有最佳气动外形，且能够通过飞行过程中的变形尽可能的规避热流烧蚀的影响，缓解了飞行器材料和结构上的压力。具体结构如图1所示。

飞行器是由左折叠翼Wl、右折叠翼Wr以及飞行器主体B三部分刚体构成，由于左右折叠翼相对飞行器主体是可以移动的，因此，可变形飞行器是一个多刚体，在折叠翼折叠运动时，质心会发生改变，会对姿态产生影响，但在航迹中，变形对质心的影响相对较小，可以忽略。折叠翼飞行器的构型参数如表1所示。

图2为折叠翼折叠方式，由图2可知，折叠翼通过折叠机构与飞行器主体相连，可以连续变形。设定折叠翼完全展开的折叠角为0°，折叠范围为[0°,153°]。采用折叠翼外形有以下几个优点：

1)采用完全收拢外形的飞行器相较于固定翼飞行器更便于运输、储存以及提高对载机的适应性。

2)飞行器加入折叠翼可以更好地适用于多任务，如巡航时完全展开提高升阻比，机动时完全收拢双翼减小阻力。

3)折叠翼飞行器可以根据飞行环境和任务需求大尺度改变自身结构，以获得最优的气动布局和操作性。

4)折叠技术的引用使飞行器的机动性、战斗力以及战时生存能力都有了一定的提高。

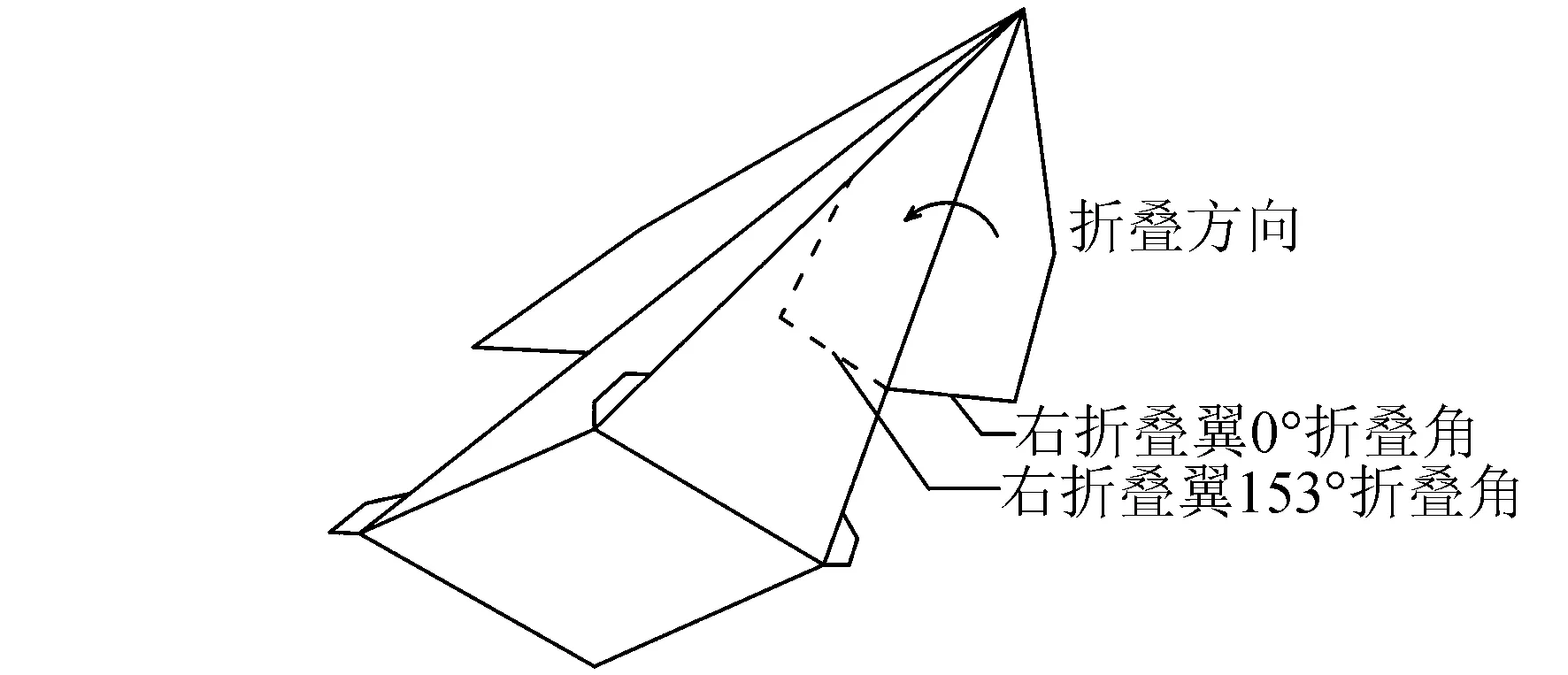
图2 折叠翼折叠方式描述Fig.2 Folding mode description of folding wing

2 再入段轨迹优化模型的建立

2.1 动力学模型

在临近空间滑翔式高超声速飞行器的再入段, 假设飞行器为无动力飞行的质点, 考虑地球为旋转椭球时, 忽略再入过程中侧力以及地球自转的影响，并取侧滑角为0。由于飞行器的变体过程影响飞行器的质心位置，对姿态的影响较大，对航迹的影响可以忽略不计，故采用单体的三自由度模型。变体高超声速飞行器再入三自由度运动方程为[12]：

(1)

式中：r为飞行器质心距离地球中心的径向距离；λ为地理经度；φ为地理纬度；V为飞行器在半速度系下相对于地球的速度；θ为航迹角；χ为航向角或者速度方位角；σ为倾斜角；m为飞行器的质量；g为重力加速度；L和D分别为作用在飞行器上的升力与阻力。

(2)

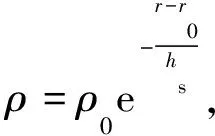
2.2 气动模型

为简化模型，做如下假设[13]：

1)忽略由于变形引起的非定常气动特性；

2)忽略高度对于升力系数和阻力系数的影响；

3)折叠角大于90°时气动参数变化较小，将[90°,153°]范围内的折叠角视为90°折叠角。

采用的折叠翼外形与传统固定翼飞行器外形不同，其气动参数是随攻角α、马赫数Ma、折叠角μ变化而变化的。利用DATCOM软件计算得到飞行器在折叠角从0°～90°每隔10°的工作状态下的升力系数和阻力系数。攻角的范围为[0°，25°]，马赫数的范围为[6,16]，折叠角的范围为[0°，90°]。通过采用下式拟合函数对气动数据进行拟合，通过用RS相关系数表示拟合程度的好坏。

(3)

式中：a与b分别为升力系数与阻力系数的各个项参数。对升力系数和阻力系数的拟合结果如表2和表3所示。

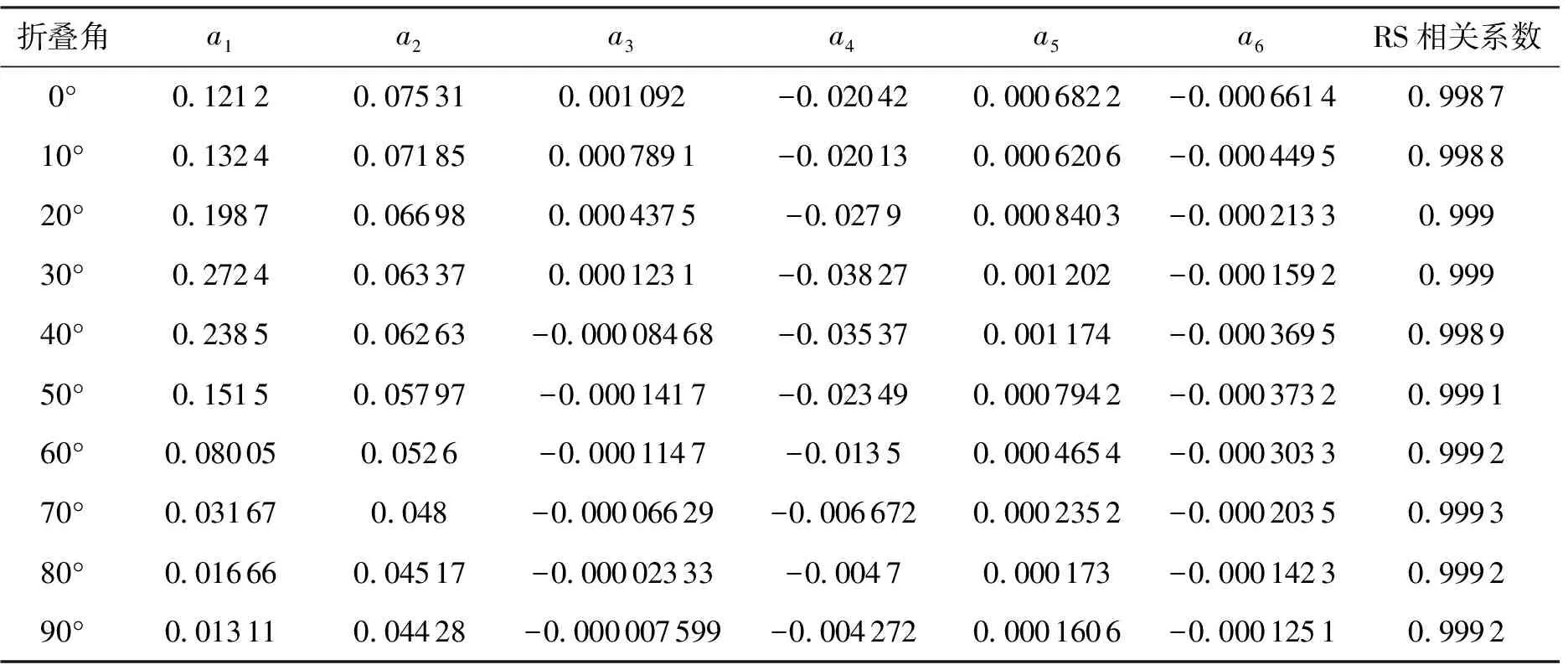
表2 升力系数拟合

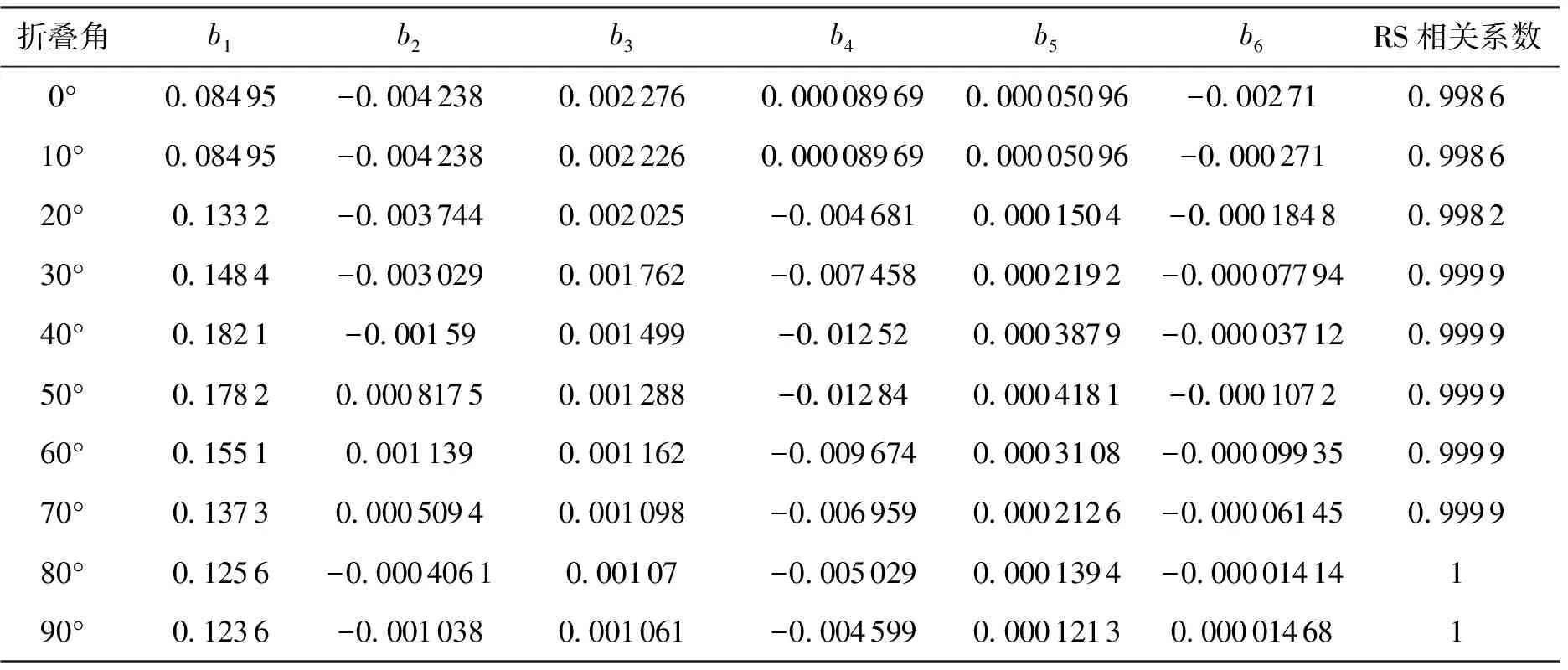
表3 阻力系数拟合

根据表2和表3可知，RS相关系数均接近于1，拟合效果很好。由于拟合气动系数是变形量μ的函数，通过将上述气动系数对攻角和马赫数的系数对折叠角进行插值，即可得到气动模型。选取0°、45°和90°三个折叠角绘制升阻比、升力系数、阻力系数图，如图3所示。

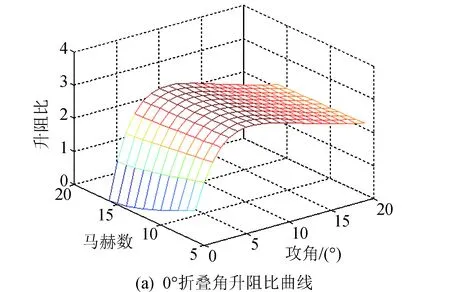
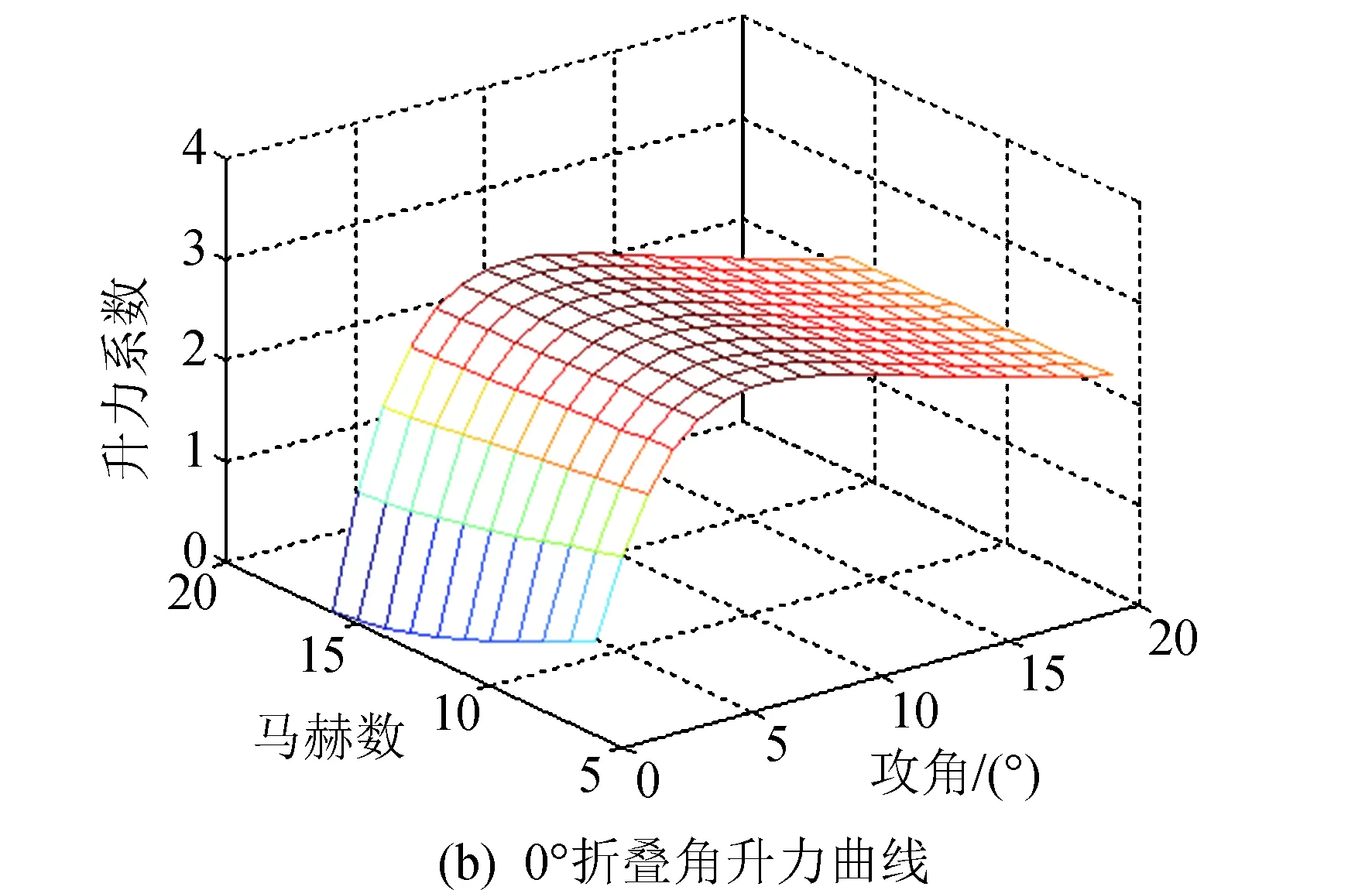
图3 不同折叠角下的气动力曲线Fig.3 Aerodynamic curves at different folding angles

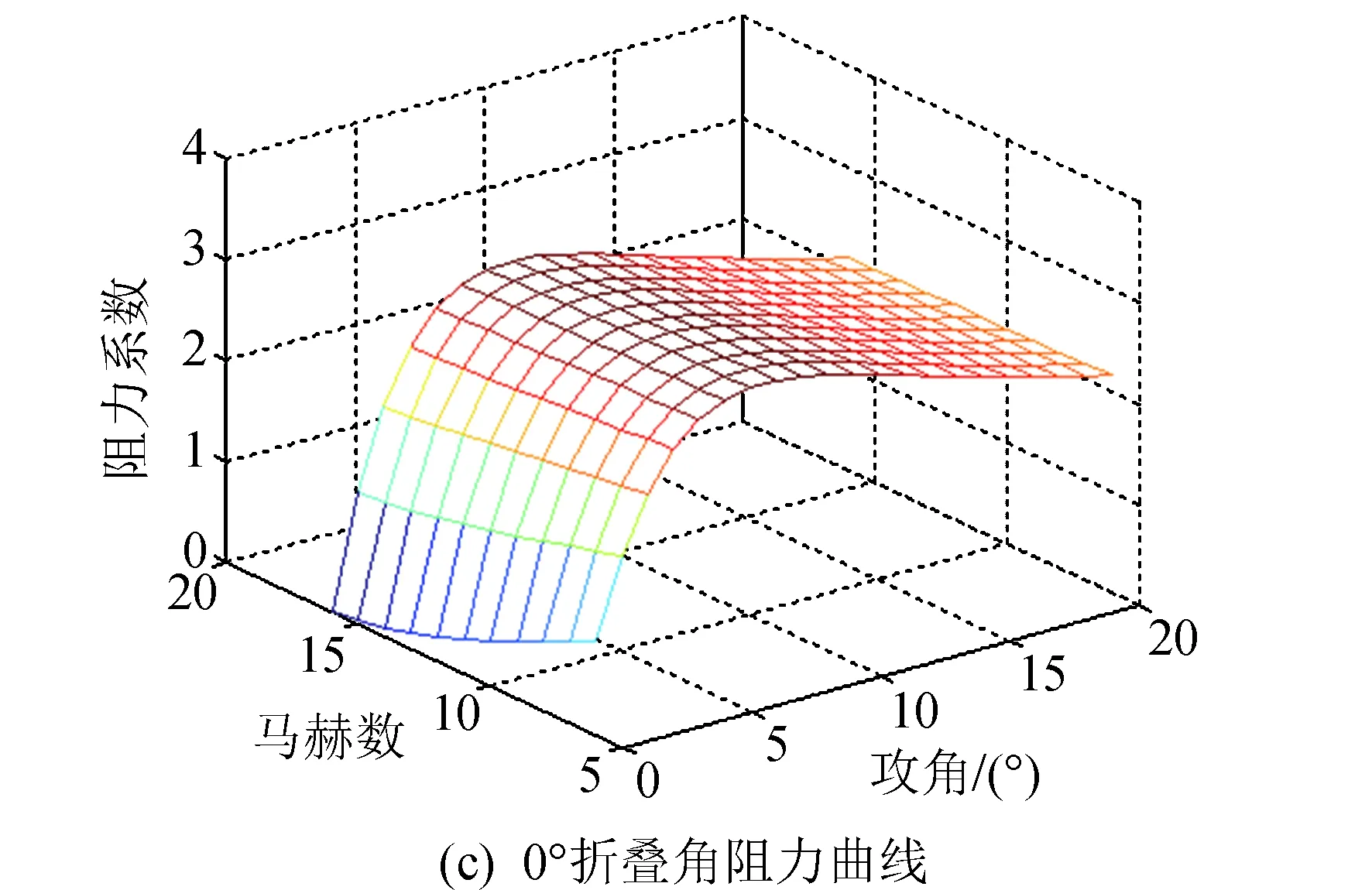
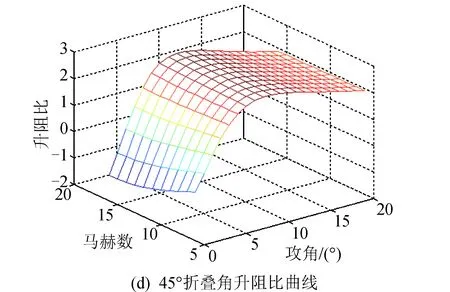
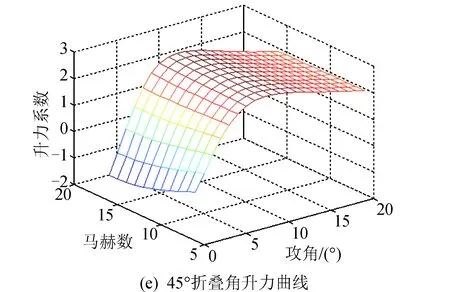
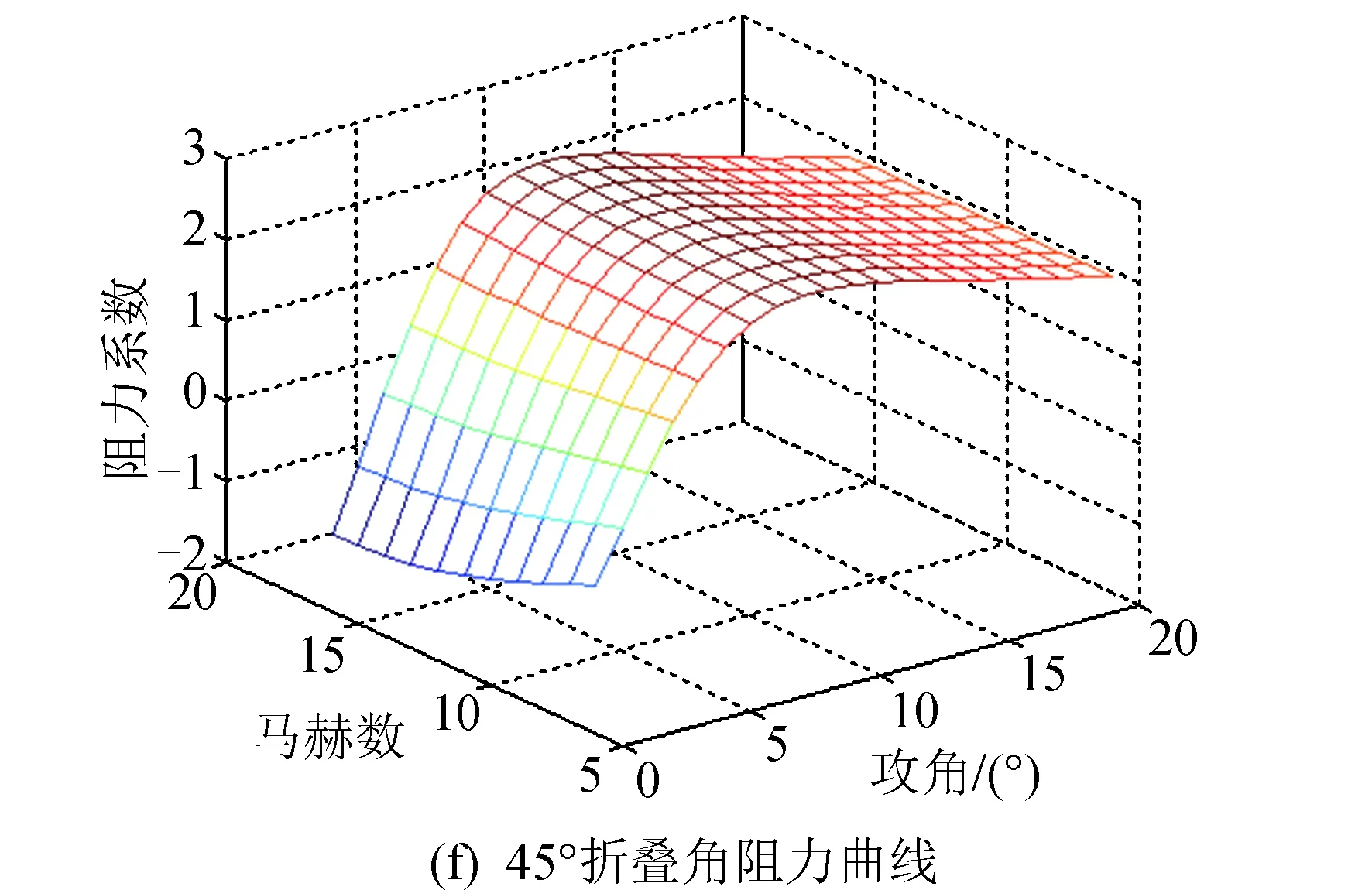
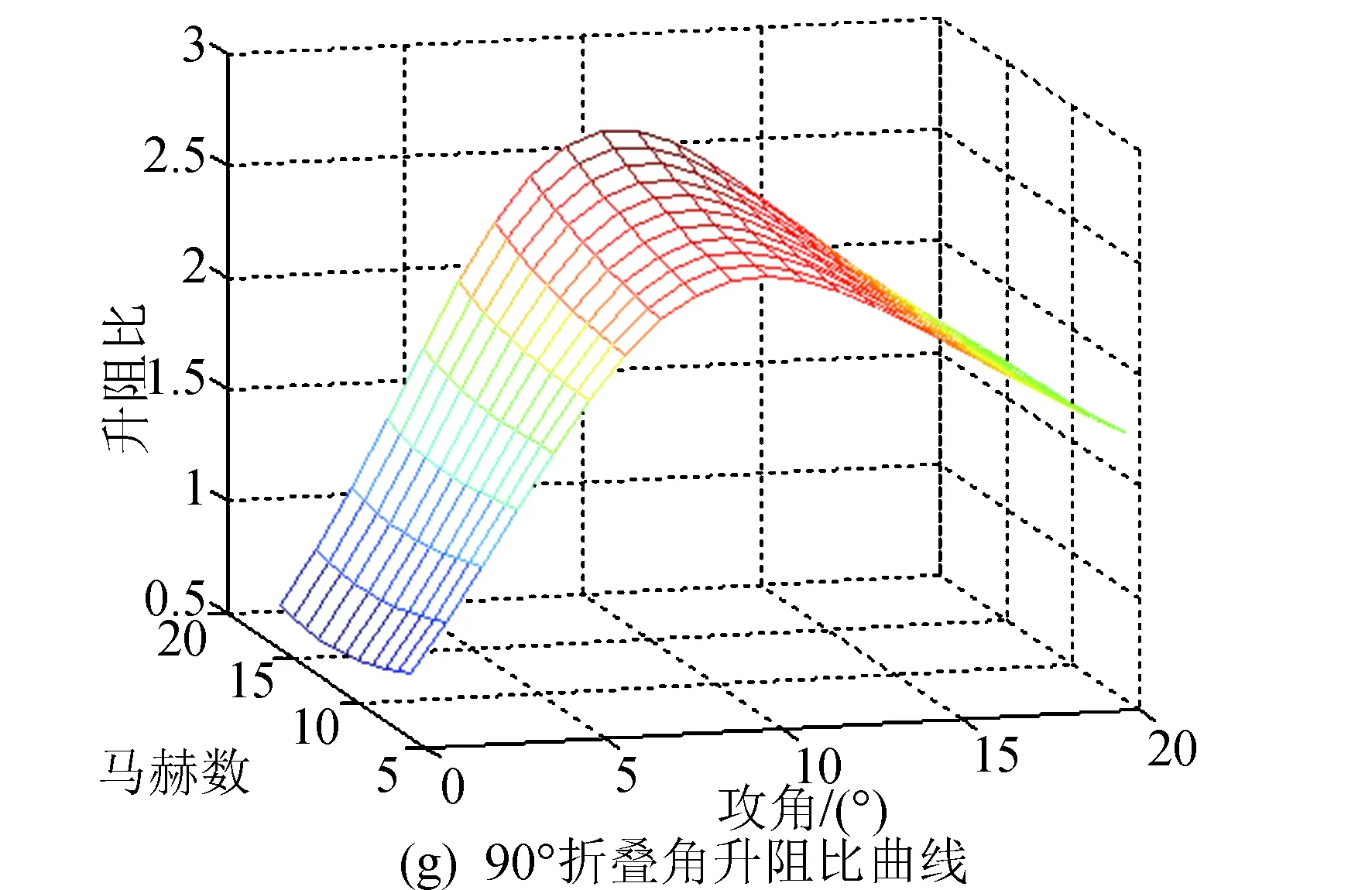
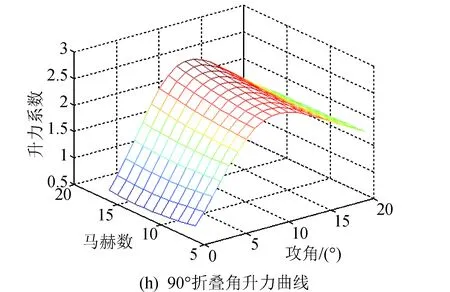
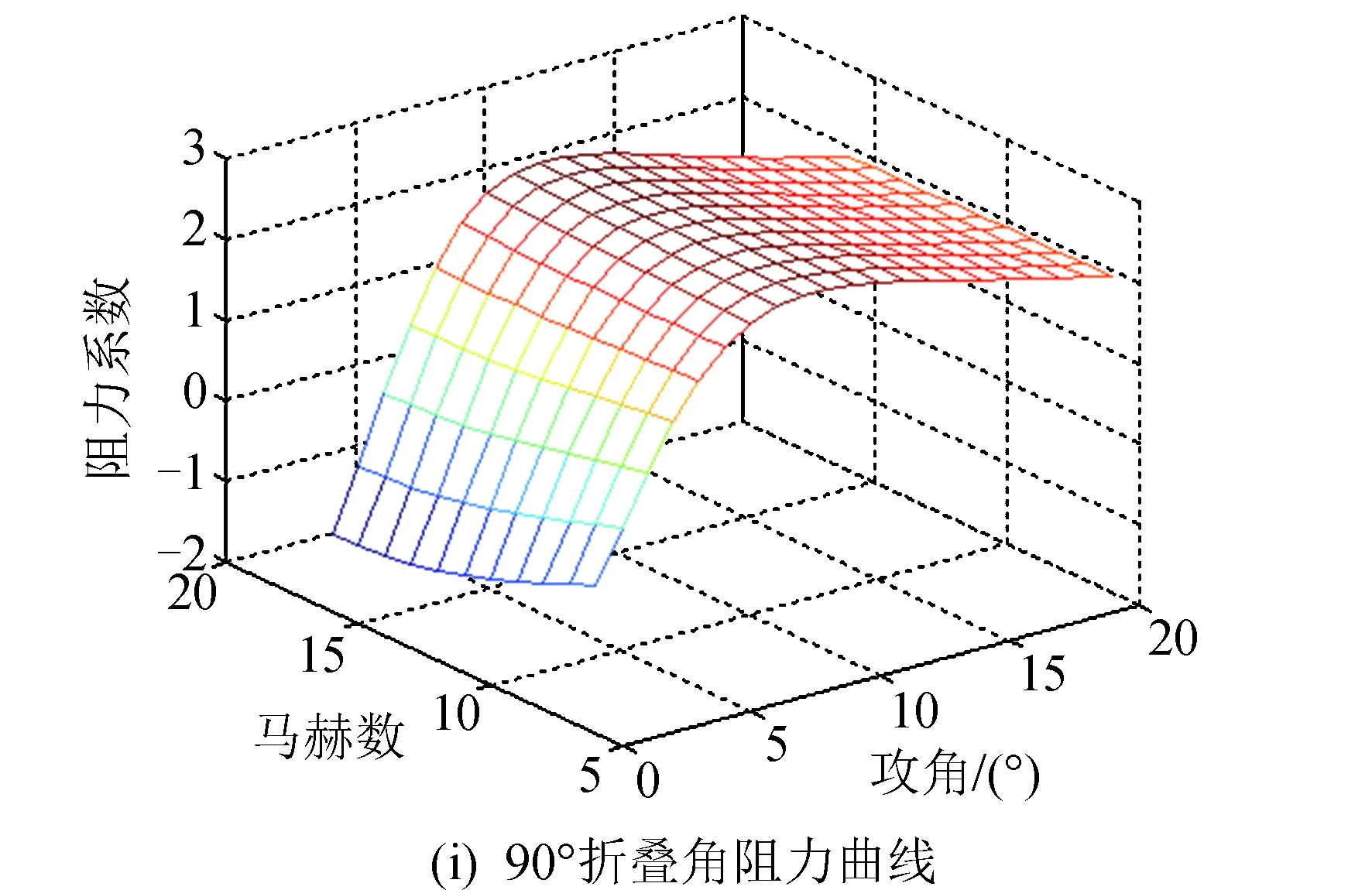
续图3Fig.3 Continued

由图3可以看出，临近空间飞行器在攻角为8°时升阻比较大，且随着折叠角的增大而逐渐减小，随着马赫数的减小而逐渐增大。

对比拟合气动系数与文献[14]和文献[5]的结果验证正确性，分别如表4和表5所示。

由表4和表5可以看出，其结果相差不大，且趋势与文献中相同。气动参数用于仿真具有正确性。

表4 拟合系数对比1(攻角8°状态)

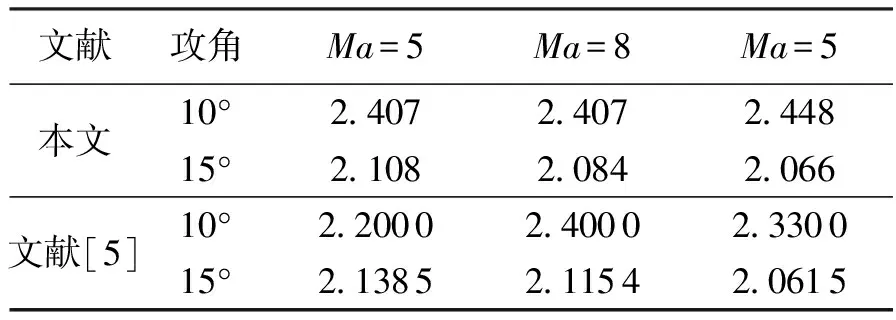
表5 拟合系数对比2

2.3 约束模型

在飞行器再入过程中, 为了保证安全稳定飞行, 飞行器需要严格满足一些约束条件, 主要包括端点约束、过程约束和状态量约束，端点约束和过程约束模型如表6所示。

表6 约束模型

端点约束规定了飞行器状态量x=[r,λ,φ,V,θ,χ]T,在再入过程中起点与终点处的取值, 定义再入起点约束和再入终点约束：

(4)

再入过程中过程约束包括热流率约束、动压约束、过载约束和准平衡滑翔条件[15]：

(1)热流率约束

由于再入过程中飞行器和大气摩擦会产生巨大的热量，因此可以考虑将飞行器气动加热效应最明显处的温度表征转化为热流率，作为再入飞行的约束条件，热流率约束一般形式为：

(5)

(2)动压约束

动压约束的一般形式为：

(6)

式中：qmax为最大动压约束。

(3)过载约束

由于工艺水平的限制，飞行器的材料和结构不可能具有无限大的强度。因此为了保证机载或者弹载设备的正常工作，必须对过载提出一定的约束，过载约束的一般形式为：

(7)

(4)拟平衡滑翔条件

拟平衡滑翔约束是用来约束飞行器平稳飞行的条件，是一个考虑飞行器控制能力的“软约束”，并不是严格要求满足的约束条件。飞行器高度为：

(8)

式中：σv为拟平衡滑翔条件下的倾斜角。

此外，受飞行器性能影响，在再入过程中，控制量u=[α,σ,μ]T和状态量x要满足一定的约束, 表示如下：

(9)

3 滑翔式高超声速折叠翼飞行器轨迹优化

本文中的模型可以直接划归为最优控制问题，高斯伪谱法可以很好地解决这一问题。高斯伪谱法是一种直接的优化方法，利用全局多项式在时间区间内对状态、控制、协态变量进行近似，采用拉格朗日插值基函数进行插值。具体原理见文献[16-17]。相对其他方法，高斯伪谱法以插值代替积分，利用离散点的设置，构造出极为稀疏的约束雅克比矩阵，对数值优化算法的求解极为有利，能够以较少的离散点、较高的速度、较高的精度得到优化问题的解。

3.1 仿真参数

端点约束和仿真条件分别如表7和表8所示。

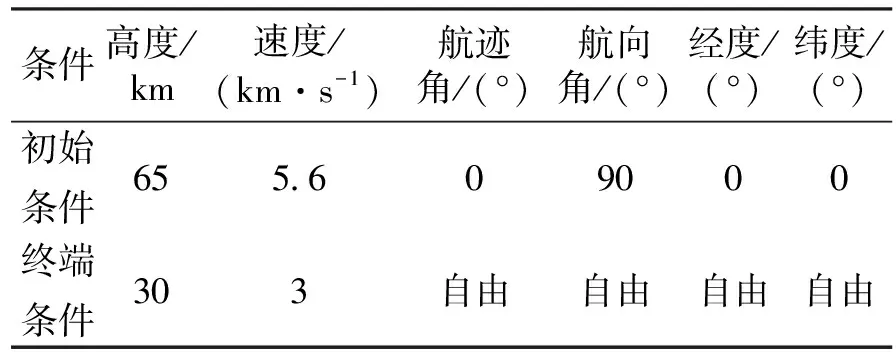
表7 端点约束

表8 仿真条件

过程约束：

3.2 拓展空间能力分析

利用高斯伪谱法，优化目标为最大纵程，即J=maxθ

由图3和图4可知，随着折叠角逐渐减小，升阻比逐渐增大，气动外形在一定程度上更加优越，因此在再入下降的过程中，射程也会逐渐增加。而折叠翼相对于固定翼外形，在不同阶段选取最优的气动外形，也比在任意角固定的折叠翼外形运行的距离远。

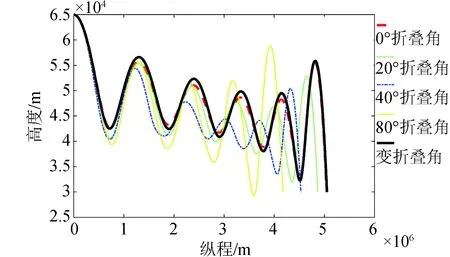
图4 高度纵程曲线Fig.4 Height longitudinal curves

固定翼外形的飞行器随着折叠角的减小，振荡下降过程的振荡幅度会变小，且再入拉起阶段的高度会更高，这也使得能量耗散更少。因此，从图4中可以看出折叠翼的振荡轨迹始终处于最优的状态，与幅度最小的固定翼飞行器飞行轨迹基本保持一致。折叠翼飞行器在飞行过程中消耗的能量更少。

以纵程为优化目标，轨迹是呈振荡下降的过程，由于终端有一个速度控制， 图4中呈现终端的拉起高度相较前几次振荡要略高。这是为了达到末态速度进行的速度管理。

图5为折叠角随时间变化的曲线，初始状态采用40°折叠角，而随后在折叠翼飞行器运行过程中，折叠角基本处于0°状态，这也从意味着0°折叠角的气动在很长一段时间都是处于相对优势的状态，这也从侧面证实了升阻比在整个再入阶段是非常重要的，升阻比越大，气动优势越明显。折叠角最后的变化也与图3的速度管理处相对应。

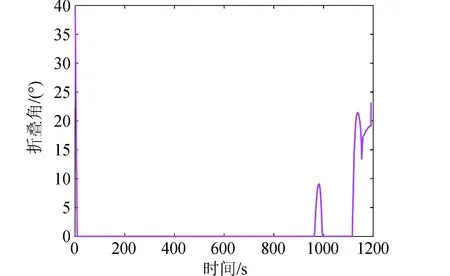
图5 折叠角随时间变化曲线Fig.5 Folding angle curve over time

图6为倾斜角随时间变化曲线，由图6可以看出，在以纵程为优化目标的情况下，倾斜角基本保持在0°，无横向机动，这可以使飞行器在整个过程中，避免浪费更多的能量。

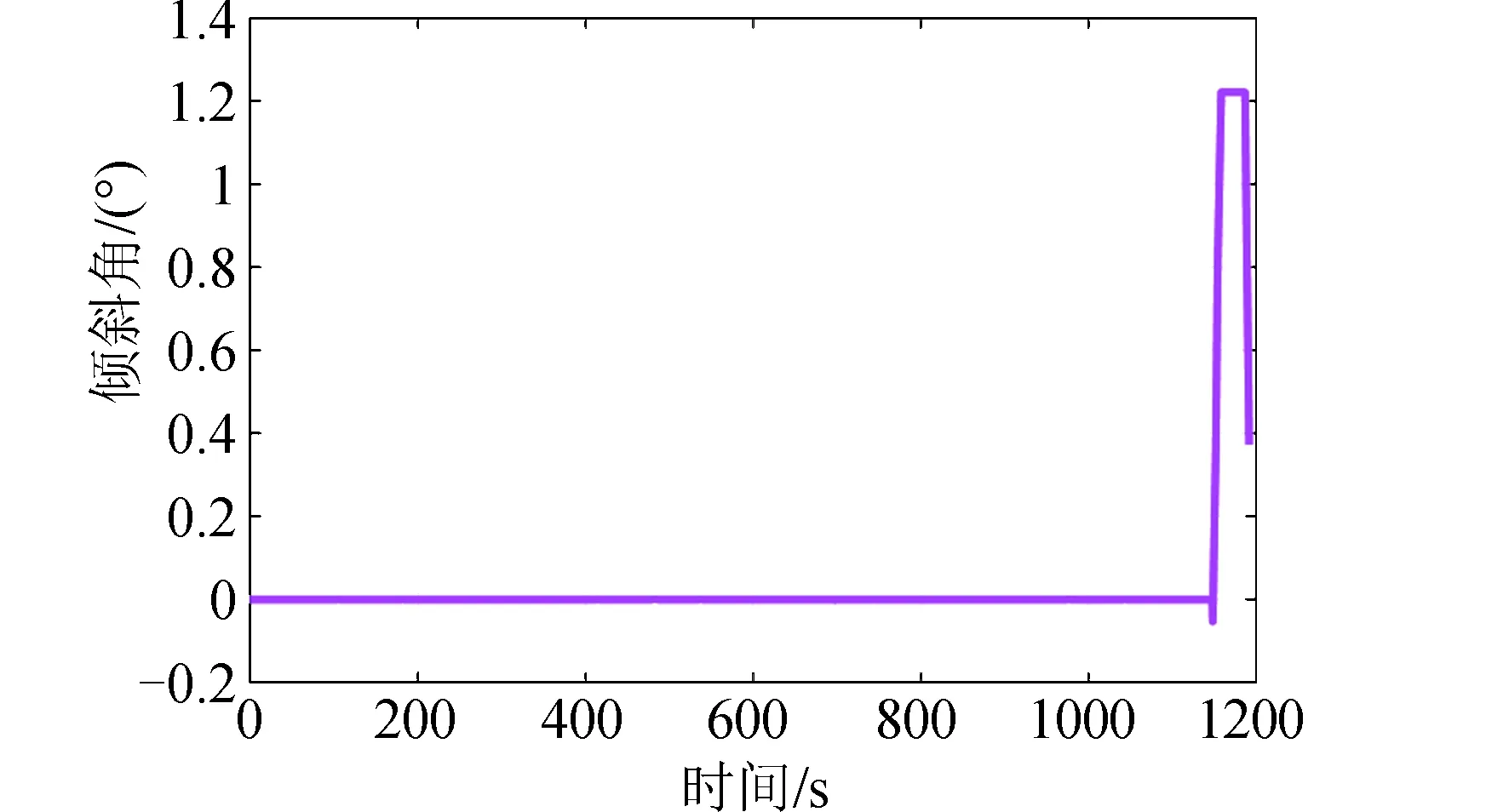
图6 倾斜角随时间变化曲线Fig.6 Slope curve over time

3.3 规避热流能力分析

图7为规避热流能力的分析图，由图7可以看出，滑翔段热流峰值一般出现在滑翔段初期，由于在滑翔段初期，大气密度较小且变化较快，速度下降较为缓慢，因此，影响热流峰值的主要因素是随着高度改变的大气密度。为了规避热流对飞行器造成的影响，飞行器往往会选择进行大攻角再入拉起，由于拉起需要足够大的升力，这也对飞行器的气动外形提出了要求。相较于固定翼外形，折叠翼外形的飞行器可以随着折叠角的改变，最快地到达最优的气动外形，也使飞行器拉起时抬升的高度较于其他固定角度飞行器更低，因此可以最大程度地规避热流对飞行器造成的影响，避免烧蚀。

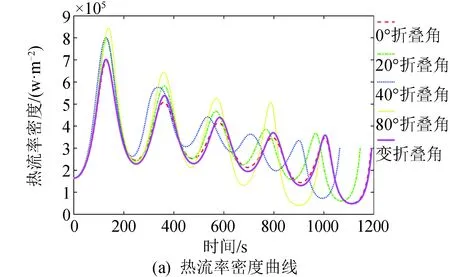
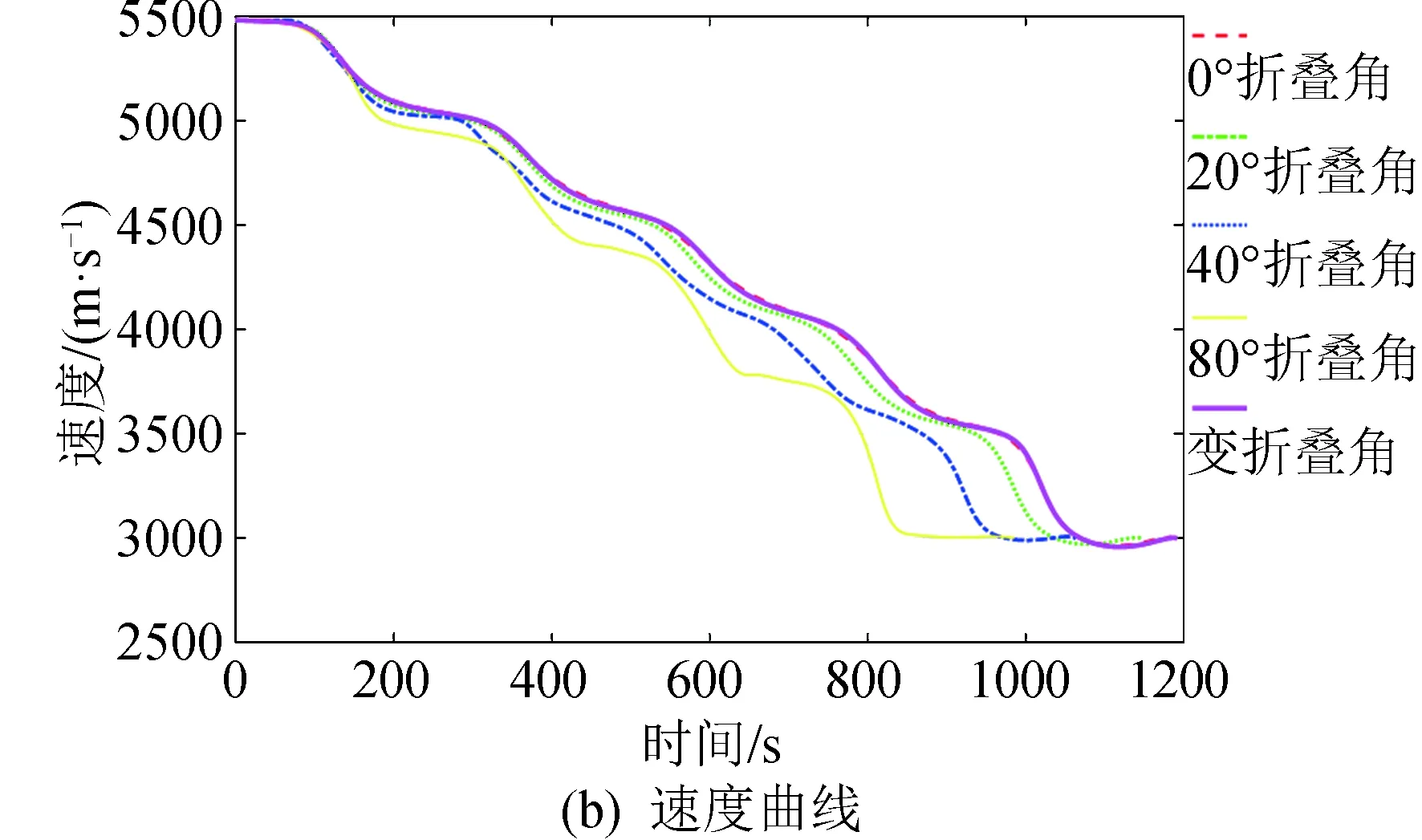
图7 规避热流能力分析Fig.7 Analysis of heat flow avoidance

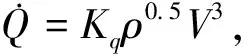
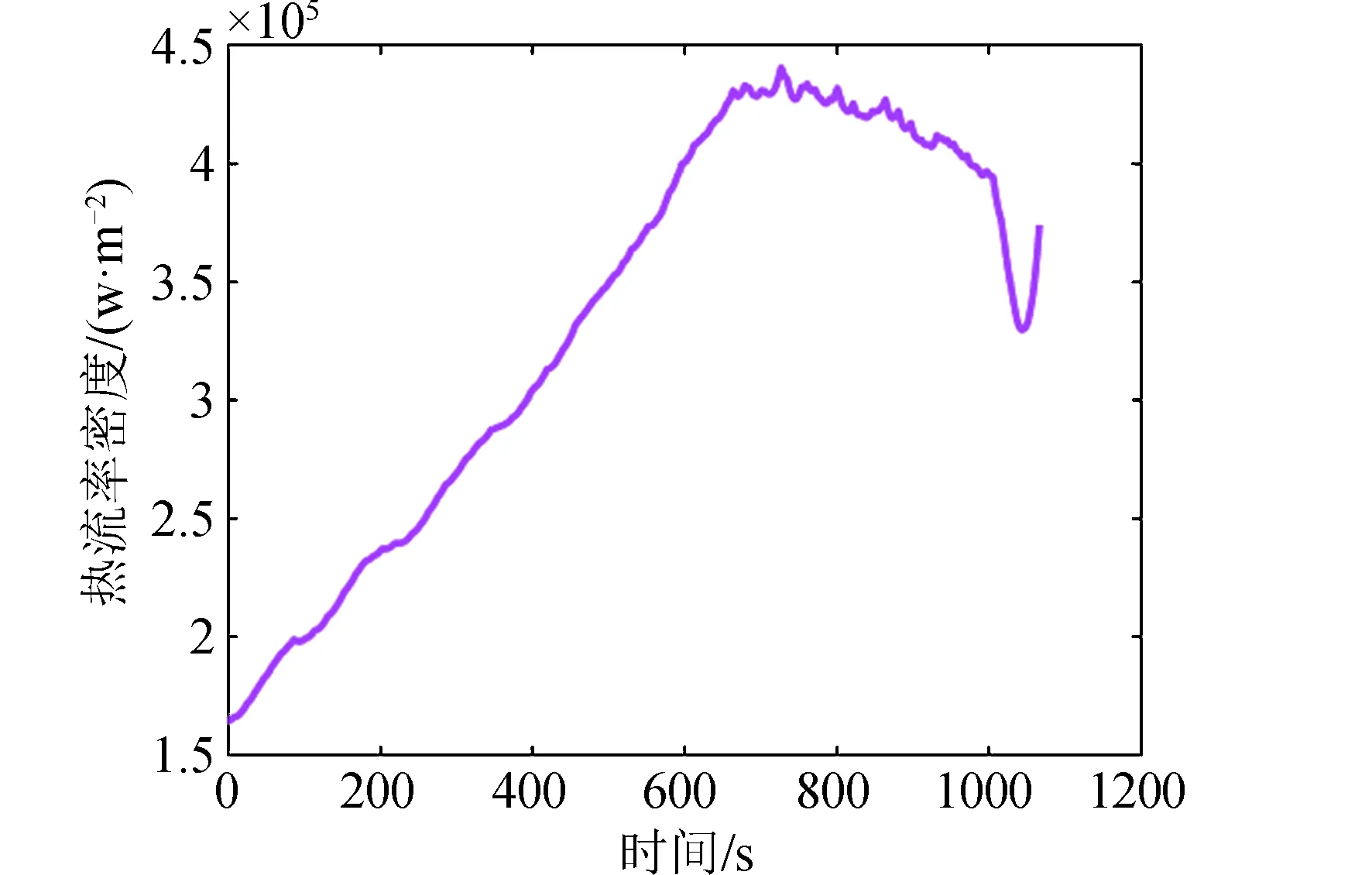
图8 折叠翼飞行器热流率曲线Fig.8 Heat flow rate curve of folding wing aircraft

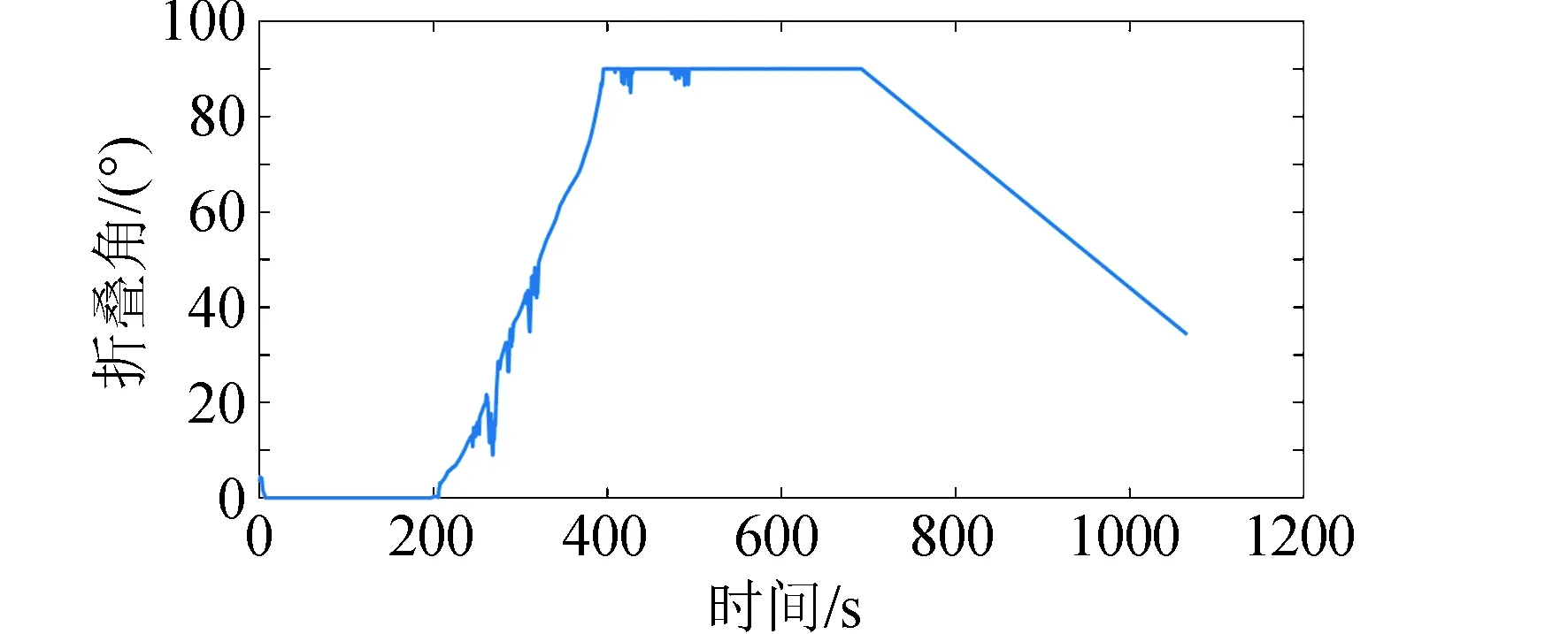
图9 折叠翼飞行器折叠角变化曲线Fig.9 Folding angle curve of folding wing aircraft

3.4 综合目标航迹优化

再入段高超声速飞行器的飞行经常综合考虑航程以及热流率，其优化函数往往是单一目标函数。大部分再入滑翔式飞行器的初始能量不能过高，很大程度上取决于既要满足热流、动压、过载的限制，还要能够具有远距离飞行的能力，变体飞行器可以很好地解决这一缺陷，经过特性研究，变体飞行器热流往往在初期达到峰值，而之后随着速度的下降，热流呈震荡下降的结果。因此，在热流率到达上限时，更改目标函数为纵程最大，拓宽飞行器的飞行距离。

图10为变体飞行器分阶段优化结果，根据图10可以看出，变体飞行器前一段采用以热流率密度上限为优化目标的航迹优化，后半段采用以航程为优化目标的航迹优化。前半段为平滑下降，后半段为振荡下降，其终端再入拉起为速度调控。变任务优化与0°折叠角航程最优和单一目标变体热流的仿真结果对比如图11所示。

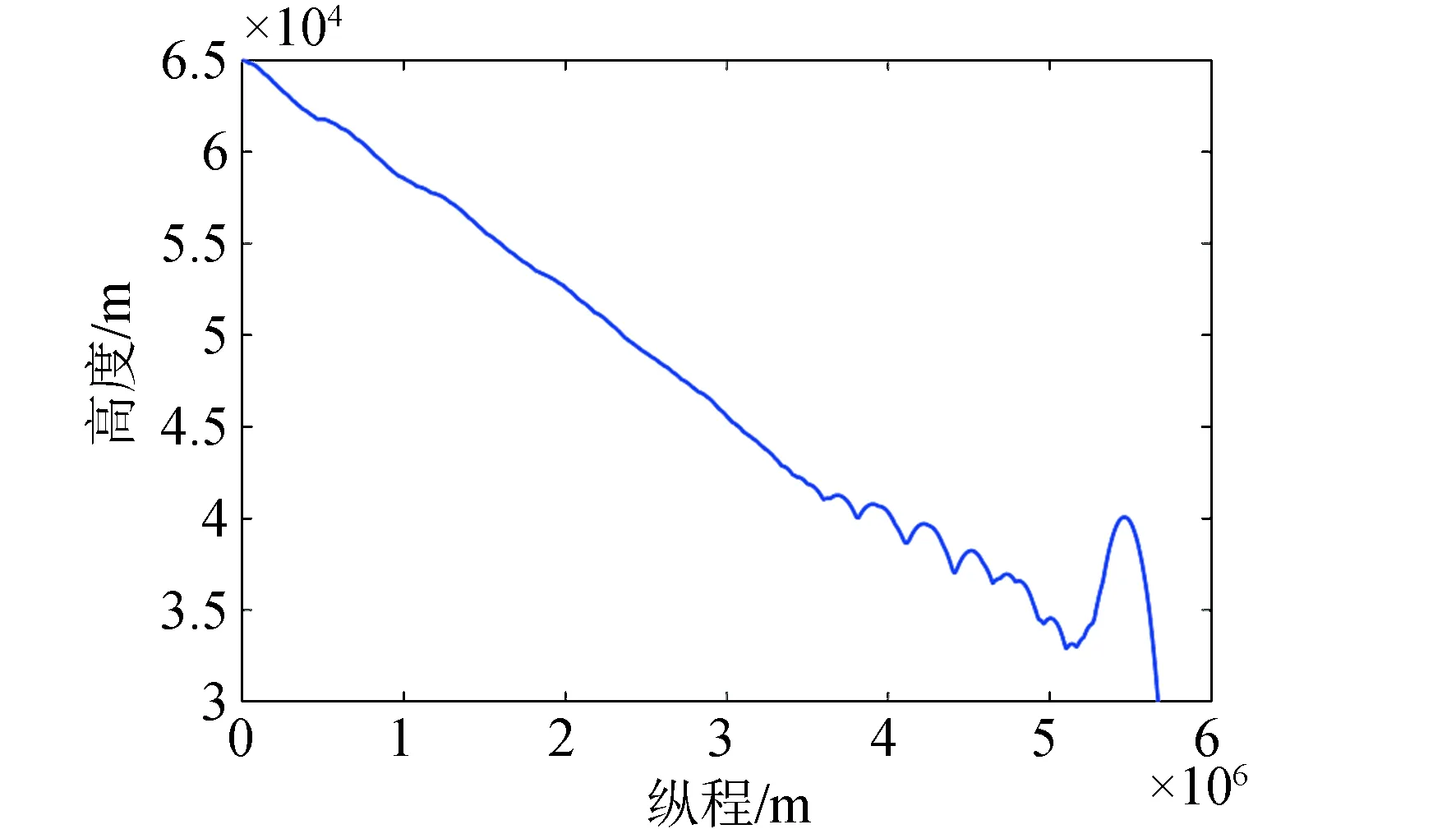
图10 变体飞行器分阶段优化结果Fig.10 Optimization results of morphing aircraft in stages

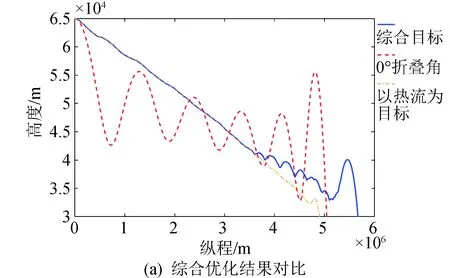
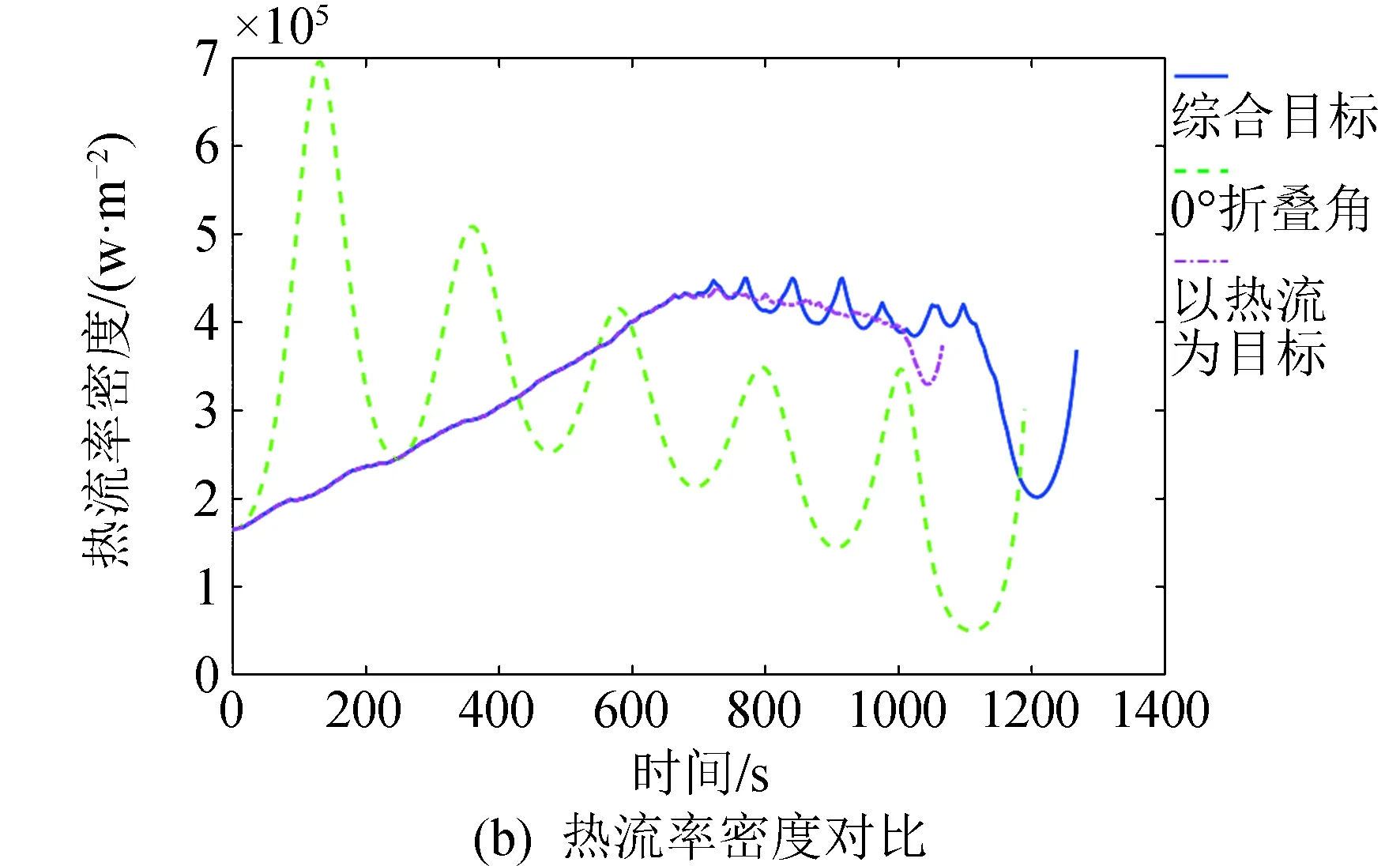
图11 综合目标航迹优化与固定翼飞行器结果对比Fig.11 Comparison of integrated target trajectory optimization and fixed-wing aircraft

将飞行器的整个过程从原本单一的固定综合指标变化为分段的目标函数。在再入初始阶段，热流为主要因素，因此考虑热流的目标函数；当过了气动热急剧加速的过程，更改为拓宽航程的目标函数。对比固定翼飞行器，考虑多优化目标的航迹优化结果热流率密度最大值减小了固定翼飞行器热流率密度最大值的35.72%，航程也相比原有固定翼航程拓宽了17.67%。

4 滑翔式高超声速变体飞行器控制分析

由于滑翔式飞行器引入变体给飞行器的控制系统造成了一定的压力，对于上述飞行器以综合指标为目标的航迹优化，控制系统的性能显得尤为重要，航迹优化中控制量攻角和倾斜角的跟踪都是影响飞行器能否跟踪优化设计的弹道的重中之重。

综合目标的航迹优化任务分为两个，前半段为考虑热流率影响的航迹优化，后半段为考虑航程的航迹优化，切换任务时会引起气动姿态角的改变，因此任务衔接处的控制为主要考虑的对象。

姿态动力学模型：

(10)

式中：γ为滚转角，向右滚转为正；ωx为滚转角角速率；ψ为偏航角，向左偏航为正；ωy为偏航角角速率；φ为俯仰角，抬头为正；ωz为俯仰角角速率。

(11)

式中：β为侧滑角；Fy为法向力；Fz为侧向力；Δα和Δβ分别为攻角和侧滑角的变化量。

ωy(-sinαcosβ-sinαsinβtanβ)+

(12)

式中：Fx为轴向力。

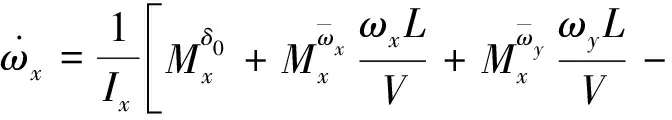
(13)

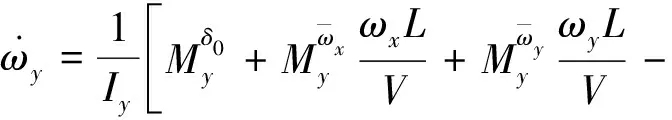
(14)

(15)

式中：Mx、My、Mz为飞行器所受绕三轴的力矩；Ix、Iy、Iz为三轴转动惯量；Sx、Sy、Sz为飞行器主体静矩(静矩为平面图形的面积与其形心到某一坐标轴距离的乘积)；Slx、Sly、Slz为折叠翼静矩。

舵偏角的绝对值小于30°，且有0.2 s延时误差。用滑模控制对飞行器680～720 s有变体的时间进行控制，由于变折叠翼引起了姿态变化需要用控制器进行稳定控制。

其跟踪效果如图12(a)所示，其气动姿态角基本能跟踪上，而舵偏角不饱和，可以验证基于综合目标考虑的轨迹优化是可以控制的。对于气动姿态角的控制，其效果与折叠角有关，攻角的阶跃突变的控制效果与折叠角的大小有关，由于不同折叠角的气动参数不同，则能够提供的最大力矩也不同。采用相同的控制器及控制器参数对采用不同折叠角的飞行器进行控制，得到的仿真结果如图12(b)所示。

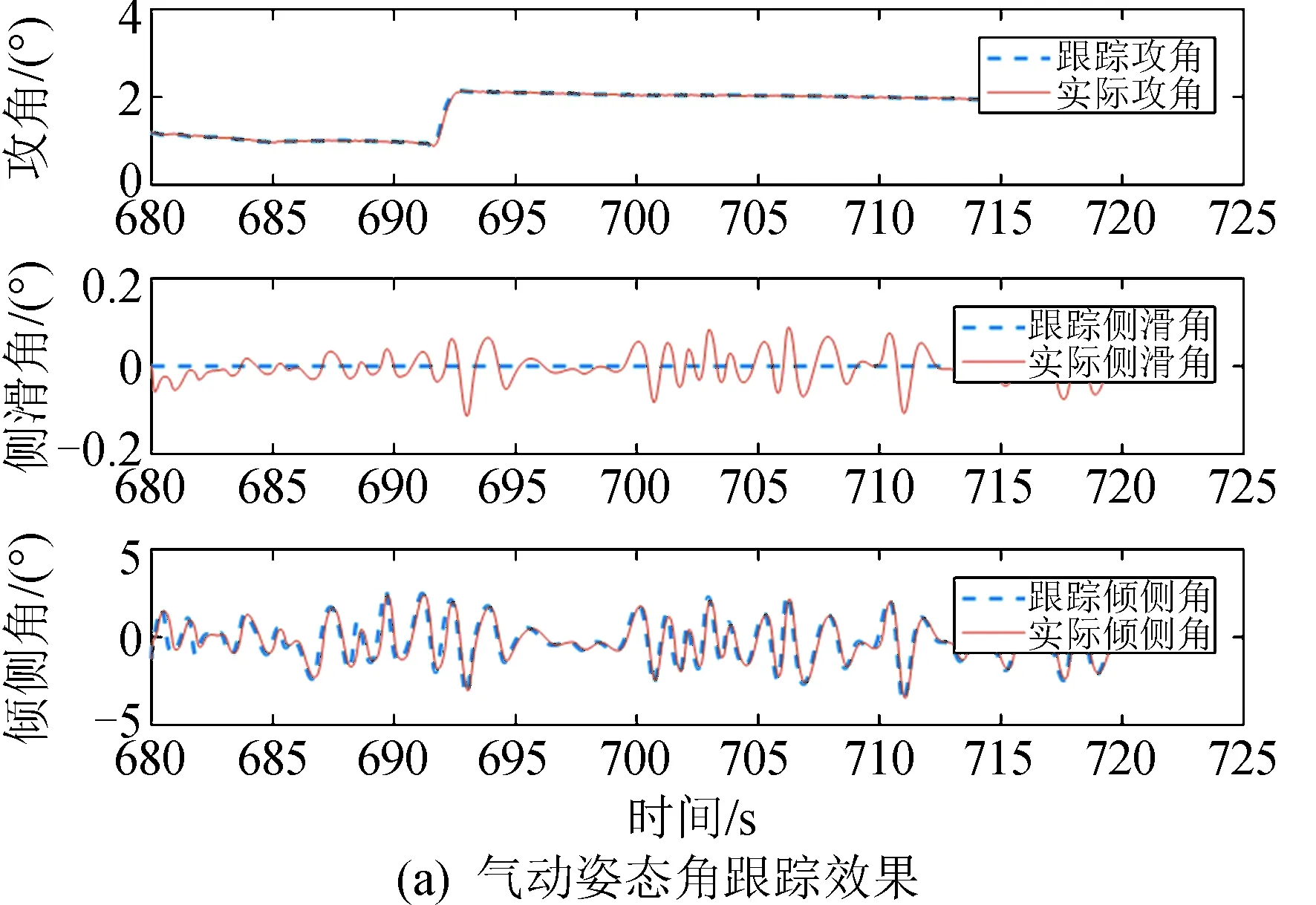
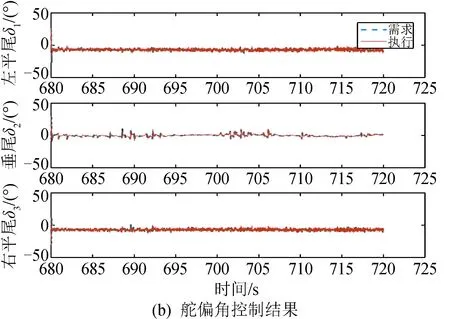
图12 气动姿态角控制效果图Fig.12 Attitude angle control results

由图13可知，折叠翼飞行器在折叠角处于中间大小时控制效果最好，而在两边0°与90°效果最差。将折叠翼为0°折叠角时的状态视为固定翼飞行器，折叠翼可以改善飞行器的控制性能，对比普通固定翼，其能够控制的最大阶跃攻角比固定翼提高了42%，大大提高了飞行器的机动性。

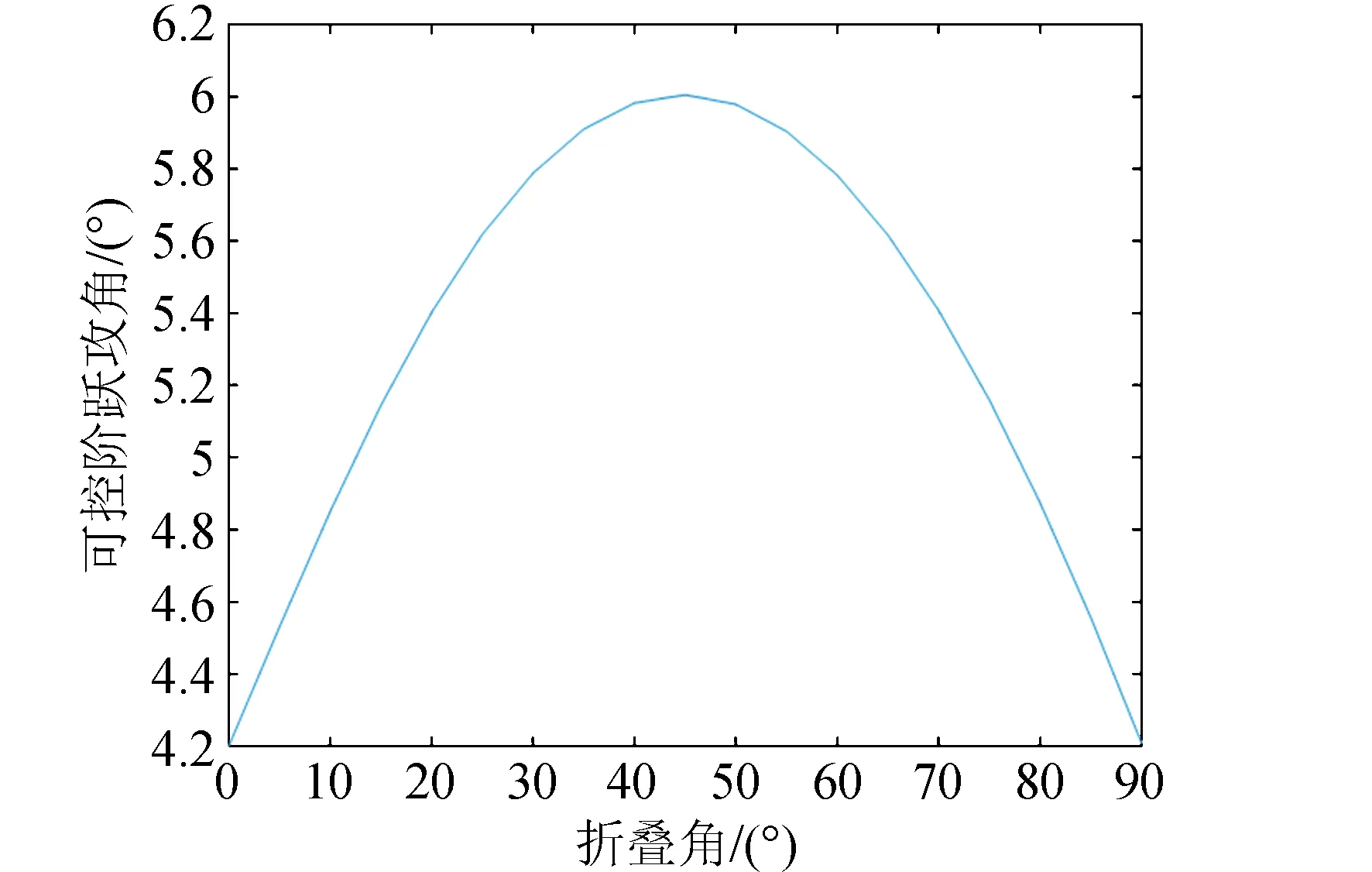
图13 折叠角与对应可控最大攻角阶跃的关系Fig.13 The relation between folding angle and attack angle

5 结束语

本文提出了在再入初期以热流率密度峰值最小为最优目标、到达再入热流峰值后以最大航程为最优目标对折叠翼飞行器进行了优化，根据特性分析以及优化结果，折叠翼飞行器的气动特性比固定翼飞行器更具有优势，优化结果相对于固定翼飞行器最优轨迹航程扩大了17.67%，热流率密度峰值下降了35.72%。此外，通过控制系统的仿真验证可知，飞行轨迹可以用控制系统进行稳定，并且具有很好的姿态机动性。

折叠翼飞行器能够通过机翼的折叠保持一个相对很好的气动优势，对于解决临近空间高超声速飞行器复杂任务以及复杂环境等问题，具有一定的实际意义。