面向空间天线的TWF复合材料性能研究

李怡晨，宋燕平，胡飞

中国空间技术研究院 西安分院，西安 710000

随着社会飞速发展，信息传输量与日俱增，对空间大型可展开天线反射器(large deployable reflector，LDR)的需求旺盛并呈增长趋势。未来对于科学、通信和地球观测等任务的实现，将需要中等(4～8 m)、大(8～15 m)甚至非常大(25 m以上)口径的反射器[1-2]。另一方面,为满足Ka及以上频段卫星通信和更高频率地球观测任务的需要，对反射器型面精度的要求越来越高[3]。

目前，在轨运行的星载大型可展开天线反射器主要为网状可展开天线反射器[4]，它具有技术成熟、面密度低和在轨飞行经验丰富等优点，但在实现高的型面精度方面具有一定的局限性[5]。网状可展开天线反射器的局限性来自两个因素[6]。首先，在较高的频率下，金属网的孔隙率和表面粗糙度会导致信号的损失和散射；其次，金属网不具有任何弯曲刚度，因此不能形成真正的抛物线形状(或其他期望的形状)。由硅橡胶作为基体的碳纤维三向纺织物(TWF)复合材料，属于一种新型的高性能材料。使用该材料作为反射器反射表面，由于其具有一定的弯曲刚度，可以获得抛物线形状，可以提供高精度的反射表面。其中碳纤维TWF提供了表面的反射性和高度稳定性；而硅橡胶则为复合材料提供了柔韧性，使得其保持容易折叠的性能。此外，它具有非常低的热膨胀系数，准各向同性的热行为。因此它可以与可展开支撑结构一起实现大口径和高精度的空间可展开天线反射器。

中外学者对TWF复合材料力学性能展开了一定的研究。大多数研究者对树脂基TWF复合材料展开了一系列研究工作，对柔性基体TWF复合材料性能研究较少。目前主要利用细观力学方法和有限元方法对TWF复合材料进行性能分析，选取材料单胞，对其进行有限元建模，通过均匀化方法得到等效的材料力学性能。其中慕尼黑工业大学Datashvili等[7]在分析硅橡胶基TWF复合材料性能时，将材料特性计算为9×9 [ABD]矩阵。本文在对柔性基体TWF复合材料力学性能进行分析时，没有采用层合板的假设。参考均匀化理论和周期性边界条件的施加方式，通过施加6个单位应变载荷最终得到等效均质材料的刚度矩阵，继而得到材料的工程常数。建立单胞有限元模型时，由于周期性边界条件的施加，需要模型为3D实体模型，而且实体模型相比于梁模型分析精度会更高。因此，对单胞进行了精细3D实体模型的建立。

为满足空间高精度可展开天线反射器各项高性能指标要求，本文将对采用不同模量碳纤维、不同纤维体积分数的硅橡胶基TWF复合材料等效性能进行分析，总结出碳纤维种类、材料纤维体积分数对单胞等效性能的影响规律，进行材料的优化设计。对于硅橡胶基TWF复合材料性能的分析，可以为其未来应用于空间大型高精度可展开天线反射器提供一定的理论基础。

1 复合材料细观力学基本理论

本节具体介绍如何由纤维、基体的材料特性最终得到整个TWF复合材料等效力学性能的理论。主要包括纤维束等效材料性能的获取、TWF复合材料几何特性及均匀化理论。

1.1 纤维束等效材料特性的获取

对单胞进行模型建立之前，首先要获取构成单胞的各向纤维束的等效材料特性。如图1所示，红色、蓝色、绿色条纹分别代表0°，-60°，+60°方向的纤维束，各个方向纤维束采用的原料均相同。

图1 纤维束示意Fig.1 Fiber bundles diagram

假设纤维束为横观各向同性材料，使用混合规则及其他一些公式[7]，由纤维、硅橡胶的材料特性以及TWF复合材料的纤维体积分数来计算等效均质的纤维束的材料特性。

纤维束拉伸模量E1和泊松比ν12使用混合规则获得，其中φf为纤维体积分数，Ef,Em分别为纤维和基体的拉伸模量：

E1=φfE1,f+(1-φf)Em

(1)

ν12=φfν12，f+(1-φf)νm

(2)

由Halpin-Tsai半经验方程得到横向拉伸模量：

(3)

其中，

(4)

参数ξ=2，取决于增强纤维的几何形状、基体的几何形状和载荷条件。

由Halpin-Tsai半经验方程得到剪切模量G12：

G12=G13=

(5)

通过求解以下二次方程获得剪切模量G23：

(6)

其中A,B,C的计算公式过长，不在此列出[14]。

由剪切模量G23，可以计算泊松比ν23：

(7)

本小节获得了构成TWF复合材料的纤维束的等效材料特性。

1.2 TWF复合材料几何特性

建立编织结构复合材料单胞模型是研究其力学性能的基础，对于选定的单胞，其几何特征指的是纤维束的空间轨迹(即位置、方向和形状)，纤维束横截面形状等[8]。

单胞(unit cell)为TWF复合材料的代表性体积单元(representative volume element，RVE)，对其进行空间平移复制即可拼造出完整织物[9]。

本文选取的单胞如图2所示。

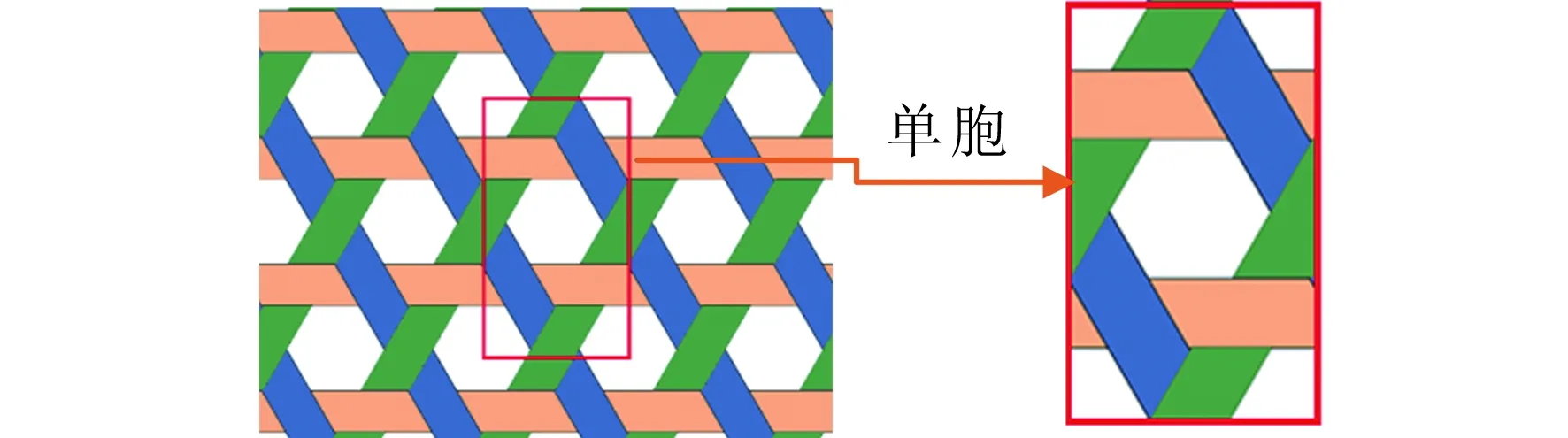
图2 三向织物及其单胞几何结构 Fig.2 Three-directional fabric and its unit cell geometry

根据TWF内0°纤维束运动轨迹可知，在一个循环内,0°纤维束从+60°方向的纤维束之上逐步扩展到-60°方向的纤维束之下，然后又回到+60°方向的纤维束之上。假设在TWF中，0°纤维束按照如图3所示的形式屈曲波动，由直线和椭圆圆弧曲线组成[10]。

图3 单胞内0°纤维束的波动形态Fig.3 Fluctuation pattern of 0° fiber bundle in unit cell

假设TWF中±60°纤维束的波动形态如图4所示。纤维束中心线走向由部分椭圆圆弧与直线组成，其形状接近于波浪状。

图4 单胞内±60°纤维束的走向示意Fig.4 Diagram of the trend of ±60° fiber bundle in unit cell

其中l1l2段、l3l4段、l5l6段为椭圆圆弧曲线(纤维束的交叠部分)，l2l3段和l4l5段(连接部分)连接相邻圆弧段并与之相切。

纤维束的横截面均假设为矩形截面。

1.3 周期性边界条件

周期性边界条件基于平移对称性变换[11]。对于尺寸为2a×2b×2c的3D复合材料，单胞的相对面之间的相对位移(见图5(a))如下：

(8)

其中下标x=a和x= -a表示相对应的面，而下标y，z表示该相对面上的相应点的共同坐标。

方程(8)可以写为：

UA-UB=FAB,UC-UD=FCD,

UE-UF=FEF

U={uvw}，下标A,B,C,D,E,F为单胞的6个面。

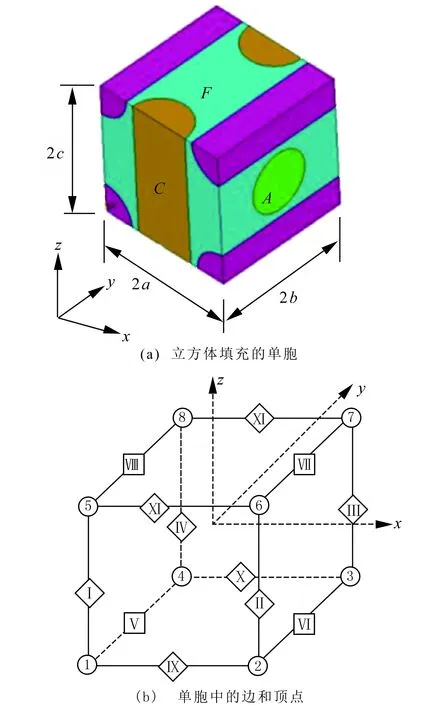
图5 单胞示意Fig.5 Diagram of unit cell

相对的边(顶点除外)的相对位移如下：

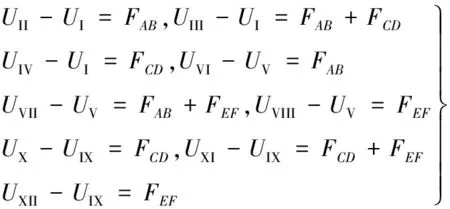
(9)

其中下标I～XII分别代表12条边，如图5(b)所示。

同样的，相对顶点之间的相对位移如下：

(10)

其中下标1～8分别代表8个顶点，如图5(b)所示。

将6个独立载荷情况应用于具有适当周期性边界条件的单胞，每一个载荷的施加都是通过施加单位宏观应变的形式。

(11)

图6为立方体单胞模型受第一种载荷情况(e11=1，其余均为0)时的边界约束与加载情况示意。

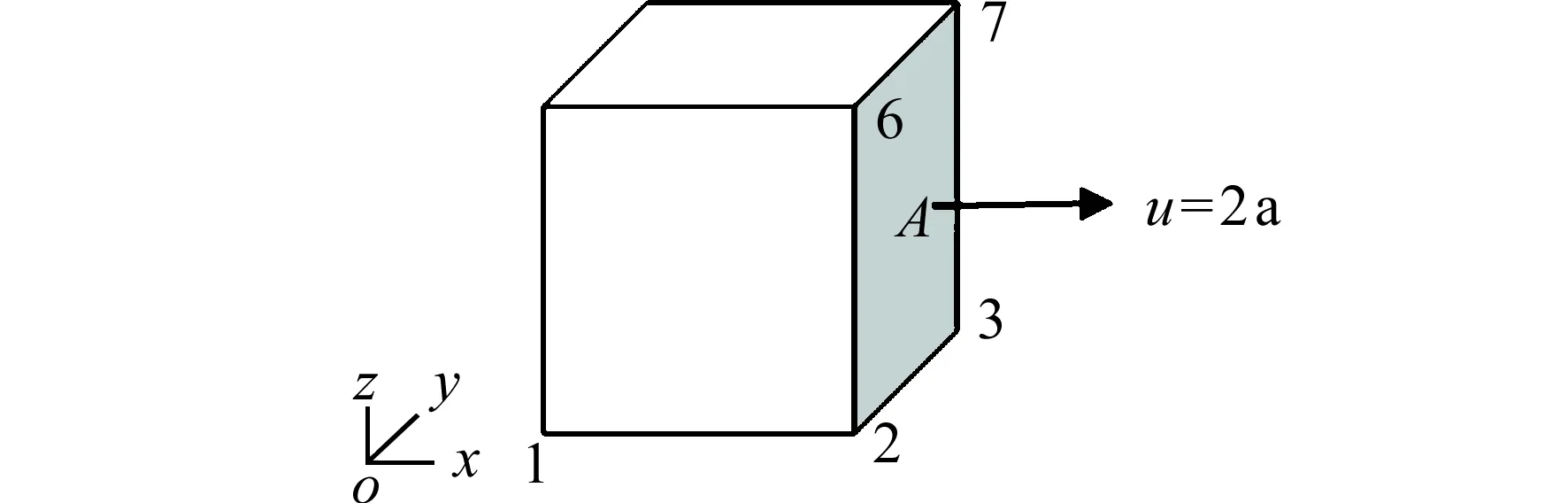
图6 有限元模型边界约束示意Fig.6 Finite element model boundary constraint diagram

约束条件为：

1.4 均匀化

由图7可以得到物体的平衡微分方程：

σij,j+fi=0

式中：(f1,f2,f3)=(fx,fy,fz)为单位体积的体力；σij,j为应力分量对坐标的偏导数，如σ12,1=σxy,x=∂σxy/∂x。

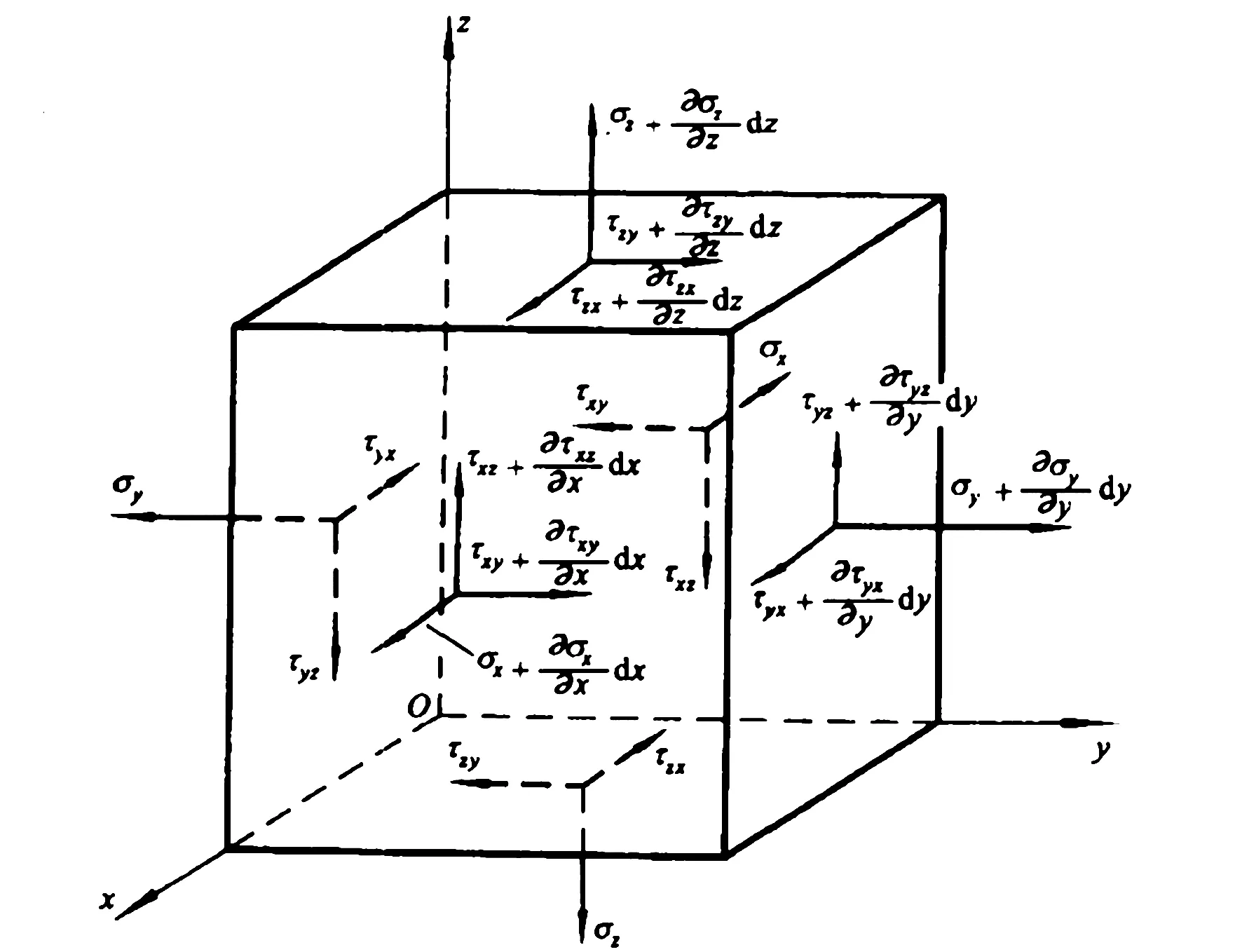
图7 物体内任意一个微分平行六面体的平衡Fig.7 Balance of any differential parallelepiped

应变位移关系和本构关系可以表示为：

式中：C为材料的刚度矩阵。

边界条件为：

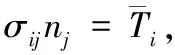
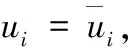
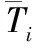
由于复合材料中刚度矩阵C会随位置快速变化，因此很难找到上述方程的解。通过均匀化理论来得到方程的解，引入一个平均模量。

视神经脊髓炎谱系病和多发性硬化患者甲状腺激素水平及甲状腺抗体的相关研究 ………………………………………………………… 陈道文，陈勇，陆杰，等 253

对于非均质材料，可以得到其平均应力应变关系如下：

(12)

式中：〈e〉、〈σ〉分别为均匀应变和均匀应力矩阵；CH为等效均匀刚度矩阵。方程(12)提供了均匀化弹性体的应力应变关系。

在有限元计算的过程中，均匀应力也可以由面平均应力值获得，如下所示：

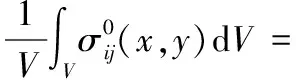
(13)

式中：S为单胞的边界；Ti为边界S上的面力。

1.5 等效力学性能的获取

材料的力学性能可以用三维本构方程来表示，其中矩阵形式如下：

(14)

Cij是弹性模量，对应于方程式(12)中的均匀化刚度矩阵分量。对单胞进行6个独立的载荷情况的应力分析，通过积分获得体积平均应力和应变，从而获得Cij。对于每个单位应变加载，可以获得等效刚度矩阵的一列，最终得到刚度矩阵C。

通过对刚度矩阵C求逆可以获得柔度矩阵S。由柔度矩阵系数，可以得到工程常数如下：

(15)

2 单胞有限元模型的建立

2.1 纤维束材料特性的计算

本文研究了不同碳纤维增强硅橡胶(Carbon Fiber Reinforced Silicone，CFRS)TWF复合材料的特性，其中碳纤维包括T300型(1K)、T700型(12K)、T800型(6K)、M40型(6K)和M60型(3K)，基体采用ZS-NJ-D955 低粘度单组份有机硅。

不同纤维和基体的材料特性如表1所示。

经过计算可以得到纤维束的等效材料性能，如表2所示(仅列出了T300/Silicone的材料特性)。

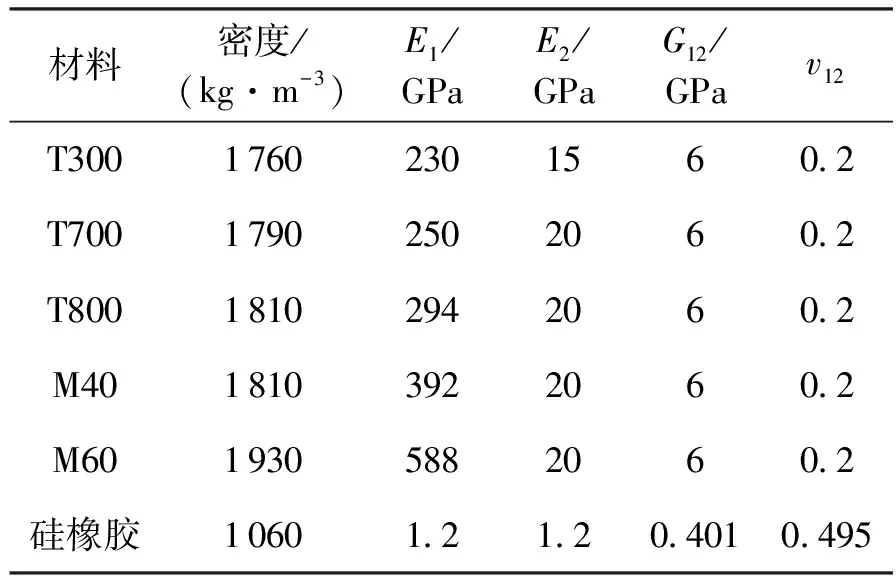
表1 纤维、基体的材料特性

表2 纤维束(纤维体积分数Vf=42%)材料性能

2.2 单胞几何模型的建立

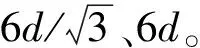
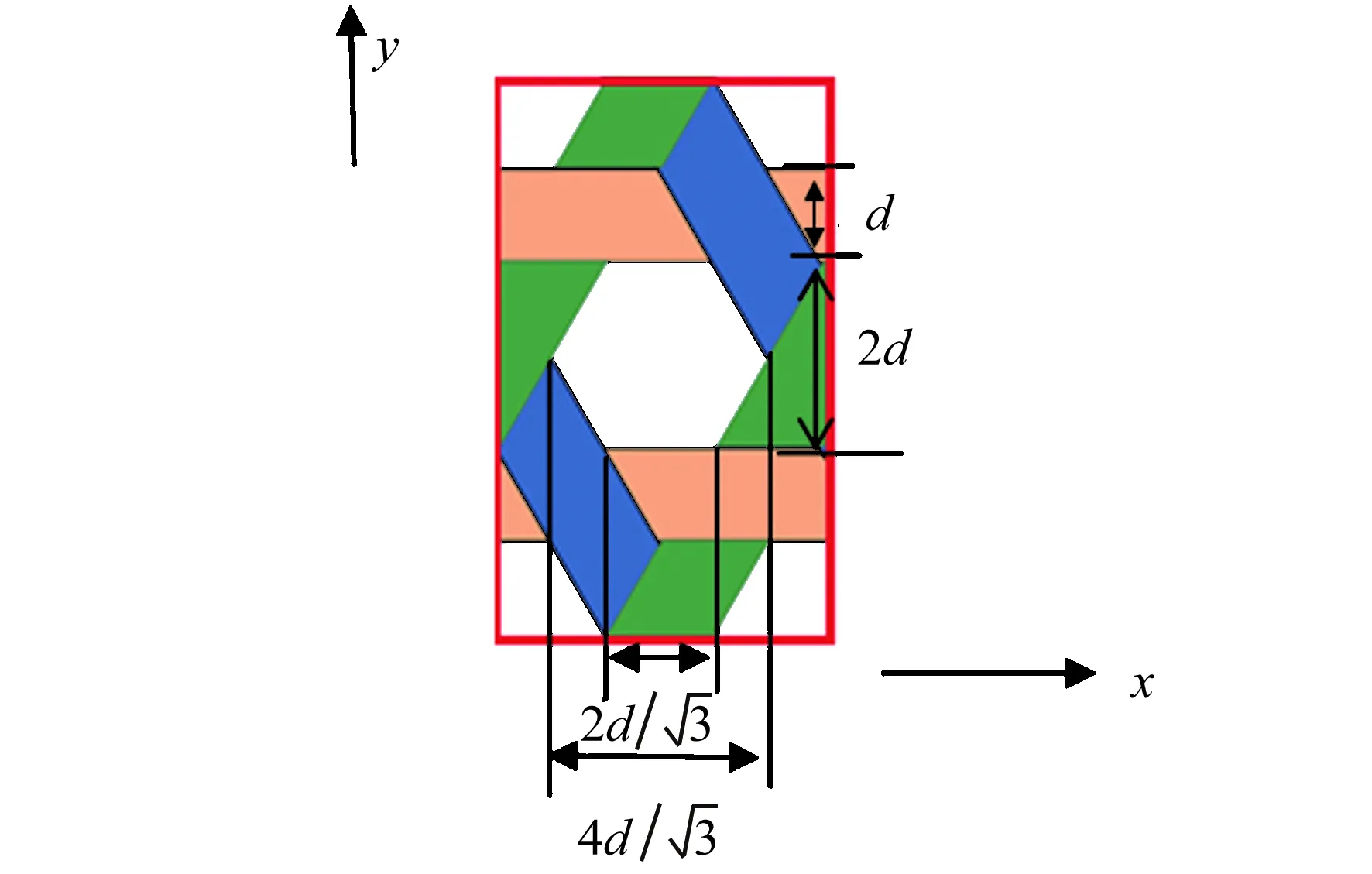
图8 单胞参数Fig.8 Unit cell parameter diagram

纤维束的波动形态示意如图9、图10所示。

图11为通过软件ProE建立起来的TWF单胞实体几何模型，由6个纤维束装配切除后得到。

其中实体为交错的纤维束，基体透明化处理，实际TWF复合材料六边形孔和4个角处应该不含基体，由于有限元分析中周期性边界条件的施加要求模型为立方体，因此采用切除的布尔运算，将模型填充为一个立方体。

可以看出模型充分考虑了纤维束的屈曲波动与交叠情况。其中d=0.9 mm，厚度h=0.075 mm，即单胞长宽高分别为3.12 mm，5.4 mm，0.15 mm。

图9 单胞内0°纤维束截面示意Fig.9 Cross section diagram of 0° fiber bundle in unit cell

图10 单胞内±60°纤维束截面示意Fig.10 Cross section diagram of ±60°fiber bundle in unit cell

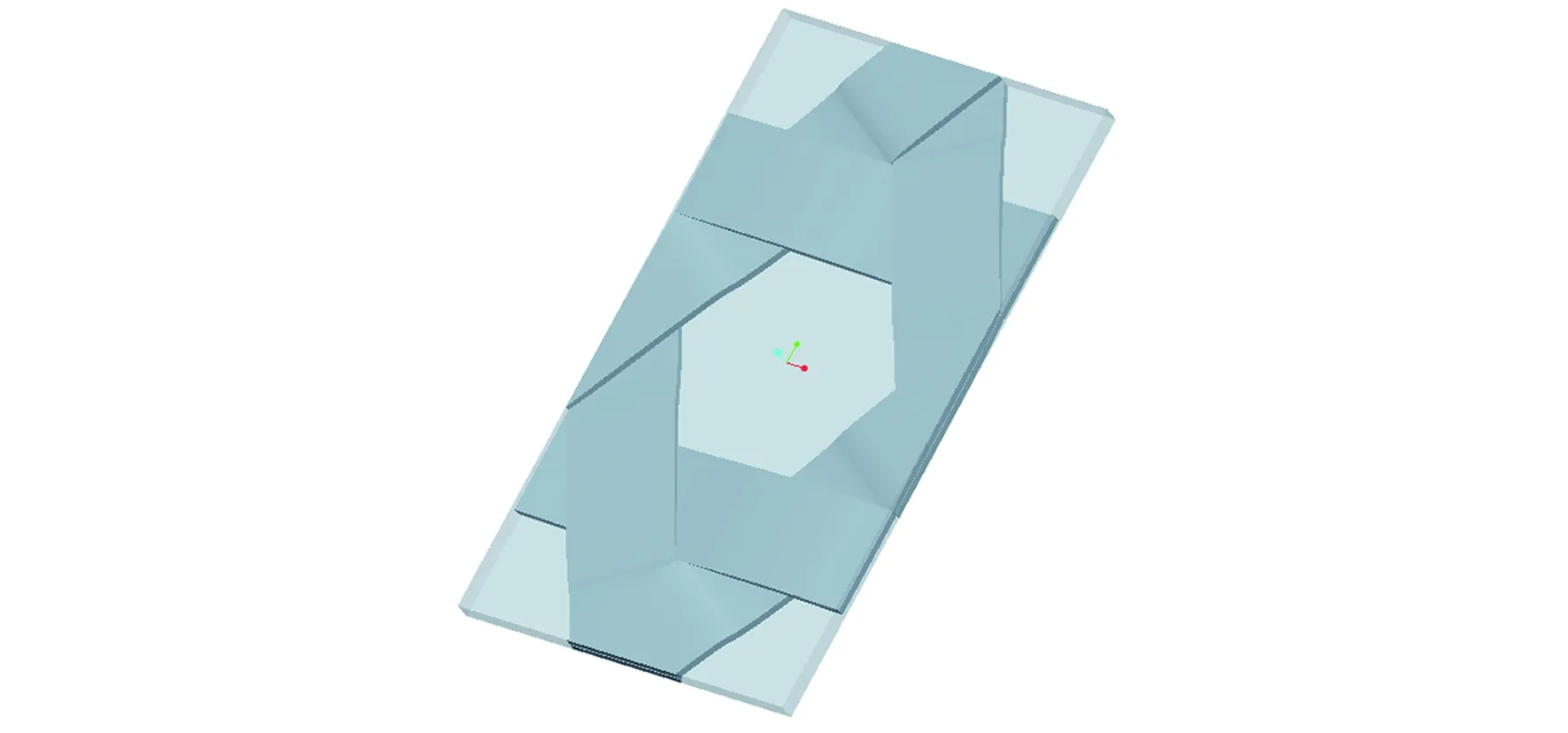
图11 单胞几何模型Fig.11 Unit cell geometry model

2.3 单胞有限元模型的建立

将在ProE中建立起来的实体几何模型导入到有限元分析软件ABAQUS中建立有限元模型。其中在赋予±60°纤维束的材料特性时，需要通过局部坐标系来指定纤维束的材料取向[12]。

对单胞采用四面体单元进行离散，单胞网格采用自由划分，如图12所示。

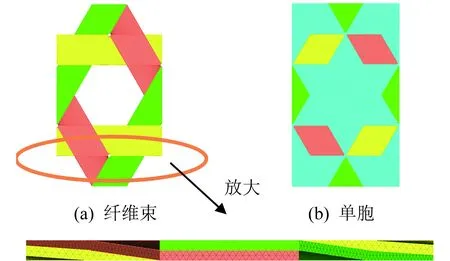
图12 单胞有限元模型Fig.12 Unit cell finite element model

3 TWF复合材料力学性能有限元分析

周期性边界条件(方程(8)～(10))，用Python语言编写代码，在ABAQUS中运行。后处理也使用Python代码实现。周期性边界条件施加程序的具体步骤如下：

2)提取装配体3个坐标方向上的最大值和最小值，计算周期性边界条件中心点的坐标值。

3)计算3个方向上边界条件中的位移初值(式(8))。

4)定义立方体上点、线、面上的节点空集合名称，共6个面，12条边，8个顶点。

5)提取X方向两个对应面上的节点集合，不包含线上的节点，并施加面位移边界条件。依次对第2、3对面施加约束条件。

6)对所有边上的点施加约束方程。首先收集各条边上的点列表，然后开始对边上的节点实际约束方程条件(除顶点以外的点)(式(9))。

7)最后对顶点施加约束方程(式(10))，完成了对8个顶点的约束方程施加，整个周期性边界条件程序运行完毕。

载荷的施加是通过在单胞表面上施加单位应变(方程(11))的形式，确定相应的应力，并由此确定表面平均应力(方程(13))，获得均匀应变和应力(方程(12))。周期性边界条件，即方程(8)～(10)，在ABAQUS中使用多点约束(MPC)来实现。对于每个单位应变，可以获得等效刚度矩阵的一列，最终得到刚度矩阵(式(14))；刚度矩阵的逆得到柔度矩阵，最终可以确定材料的工程常数(式(15))。

得到T300碳纤维增强硅橡胶复合材料(纤维体积分数为42%)的刚度矩阵C：

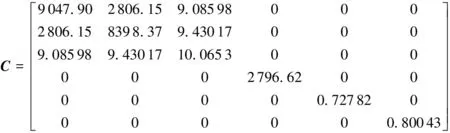
最终得到工程常数如表3所示。

表3 TWF复合材料(Vf=42%)力学特性

4 参数讨论与分析

由于本文研究的材料未来是用于高精度可展开天线反射器反射表面，为满足天线反射器各项高性能指标要求，对材料的力学性能有比较高的要求。本文将碳纤维的模量和纤维体积分数作为两个关键参数，分析其对硅橡胶基TWF复合材料等效性能的影响，可以进行材料的优化设计。

4.1 碳纤维种类对单胞等效性能的影响

本文研究了5种不同碳纤维对于单胞等效性能的影响规律。图13给出了单胞等效性能随碳纤维种类变化的变化规律，其中单胞等效性能包括拉伸模量E11,E22,E33，剪切模量G12,G23,G31，泊松比v12,v23,v31。

从图13可以看出随着碳纤维模量的增大，等效材料性能面内拉伸模量E11,E22均增大；而且E11与E22之间的差距越来越明显，即材料的面内各向异性更加明显；从图14可以看出随着碳纤维模量的增大，等效的横向拉伸模量E33也增大。由于T300的横向模量小于其他几种碳纤维的横向模量，因此等效的横向拉伸模量E33也比较小，导致曲线有一个跳跃。

从图15可以看出随着碳纤维模量的增大，等效材料性能面内剪切模量G12增大；而且增大的越来越多；从图16可以看出随着碳纤维模量的增大，横向剪切模量G23基本保持不变；横向剪切模量G31呈缓慢增加的趋势。

从图17可以看出随着碳纤维模量的增大，泊松比v12,v23,v31均基本保持不变，说明泊松比对于碳纤维种类的变化并不敏感。

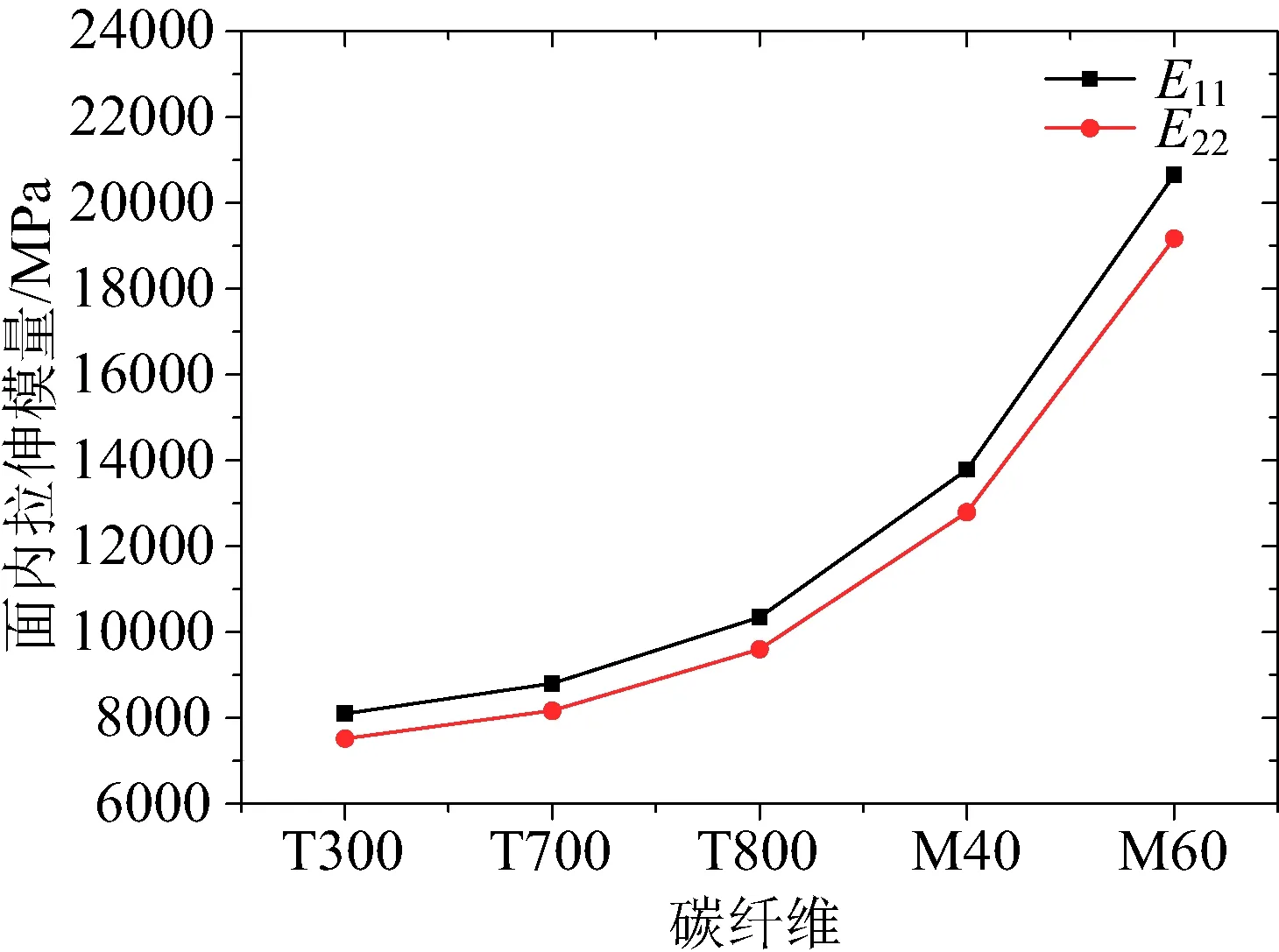
图13 碳纤维种类对面内拉伸模量的影响Fig.13 Effect of fiber types on in-plane tensile modulus

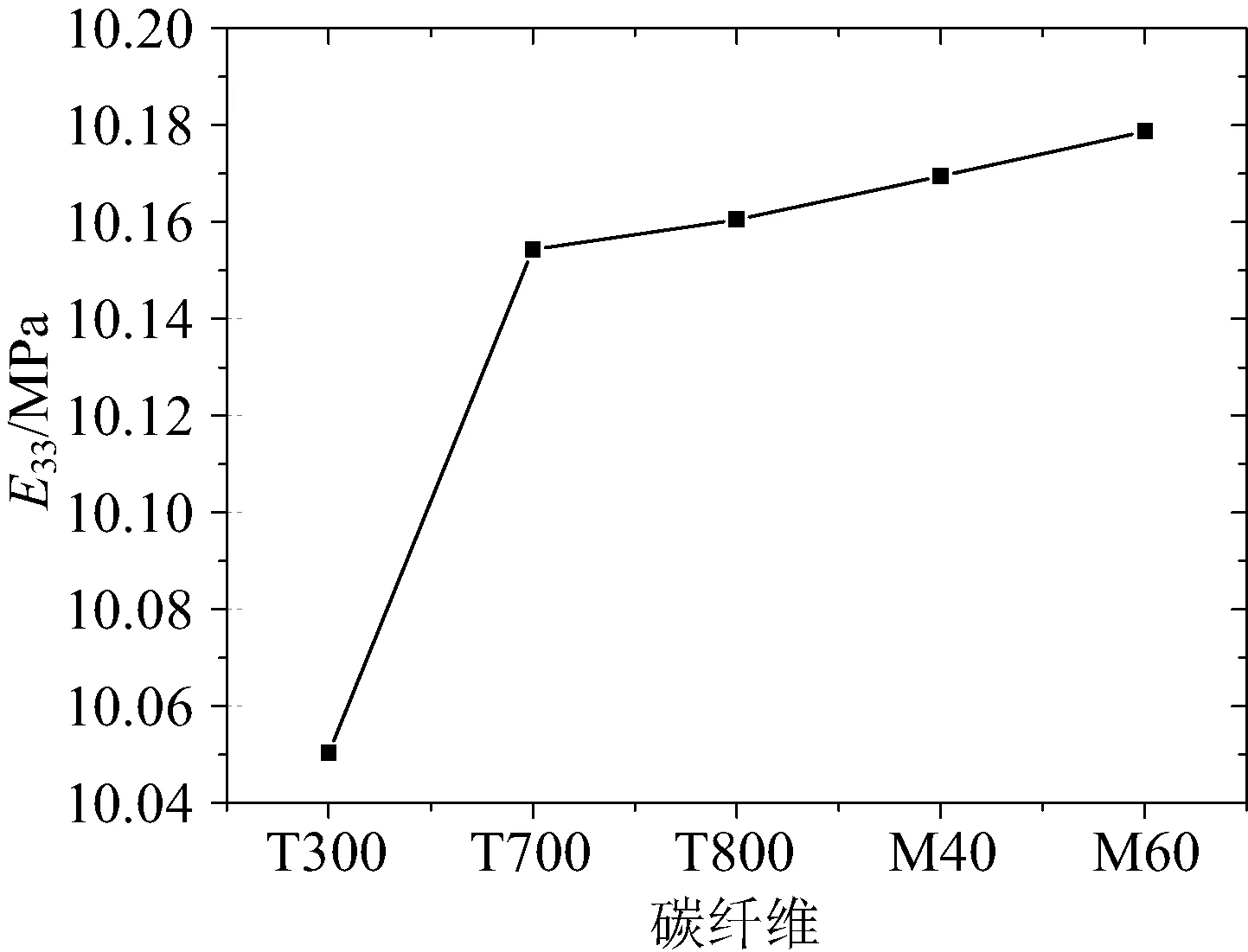
图14 碳纤维种类对横向拉伸模量E33的影响Fig.14 Effect of fiber types on E33

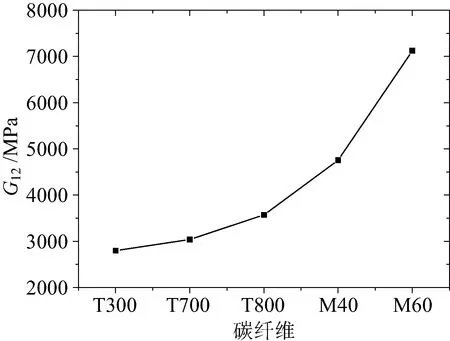
图15 碳纤维种类对面内剪切模量的影响Fig.15 Effect of fiber types on in-plane shear modulus

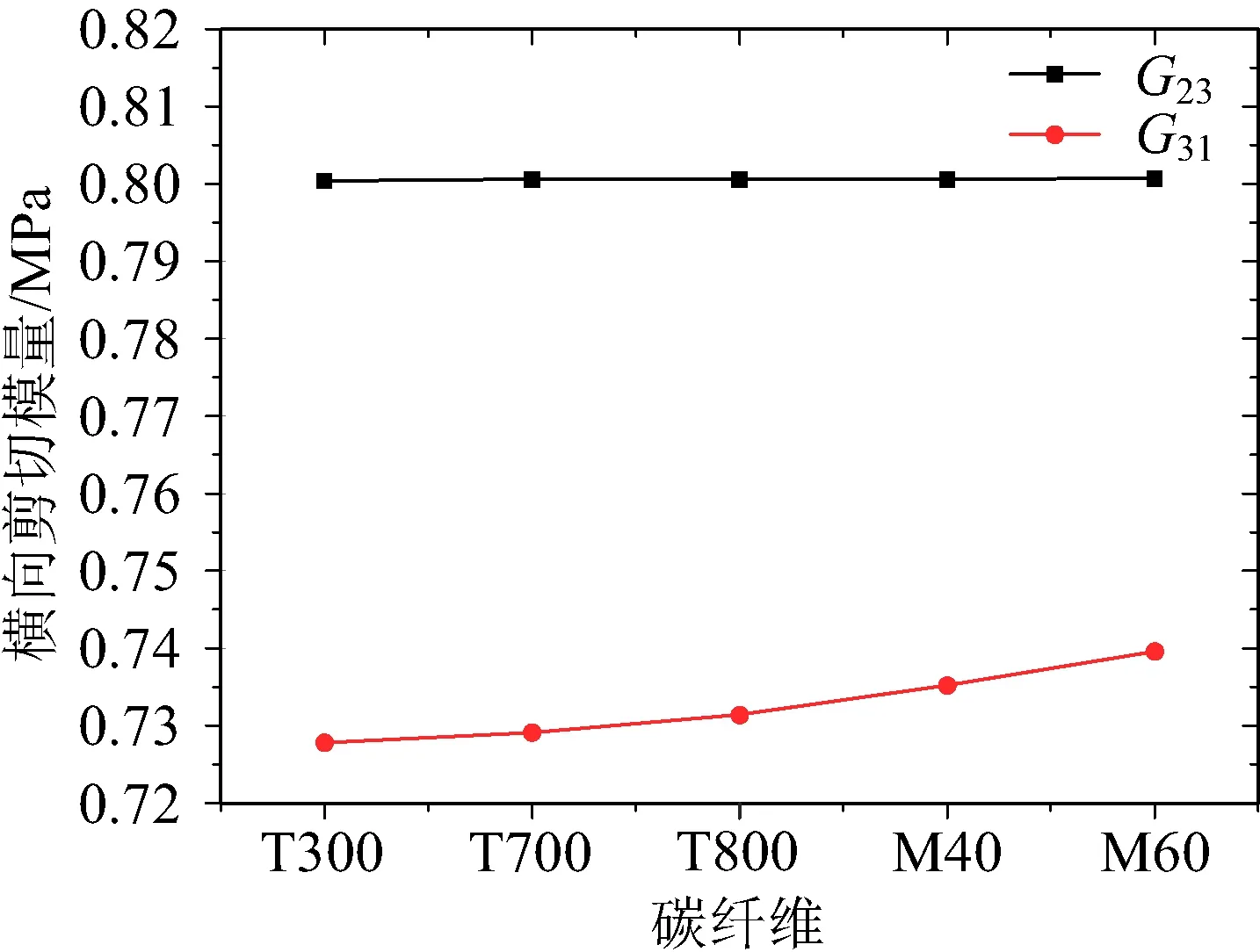
图16 碳纤维种类对横向剪切模量的影响Fig.16 Effect of fiber types on transverse shear modulus

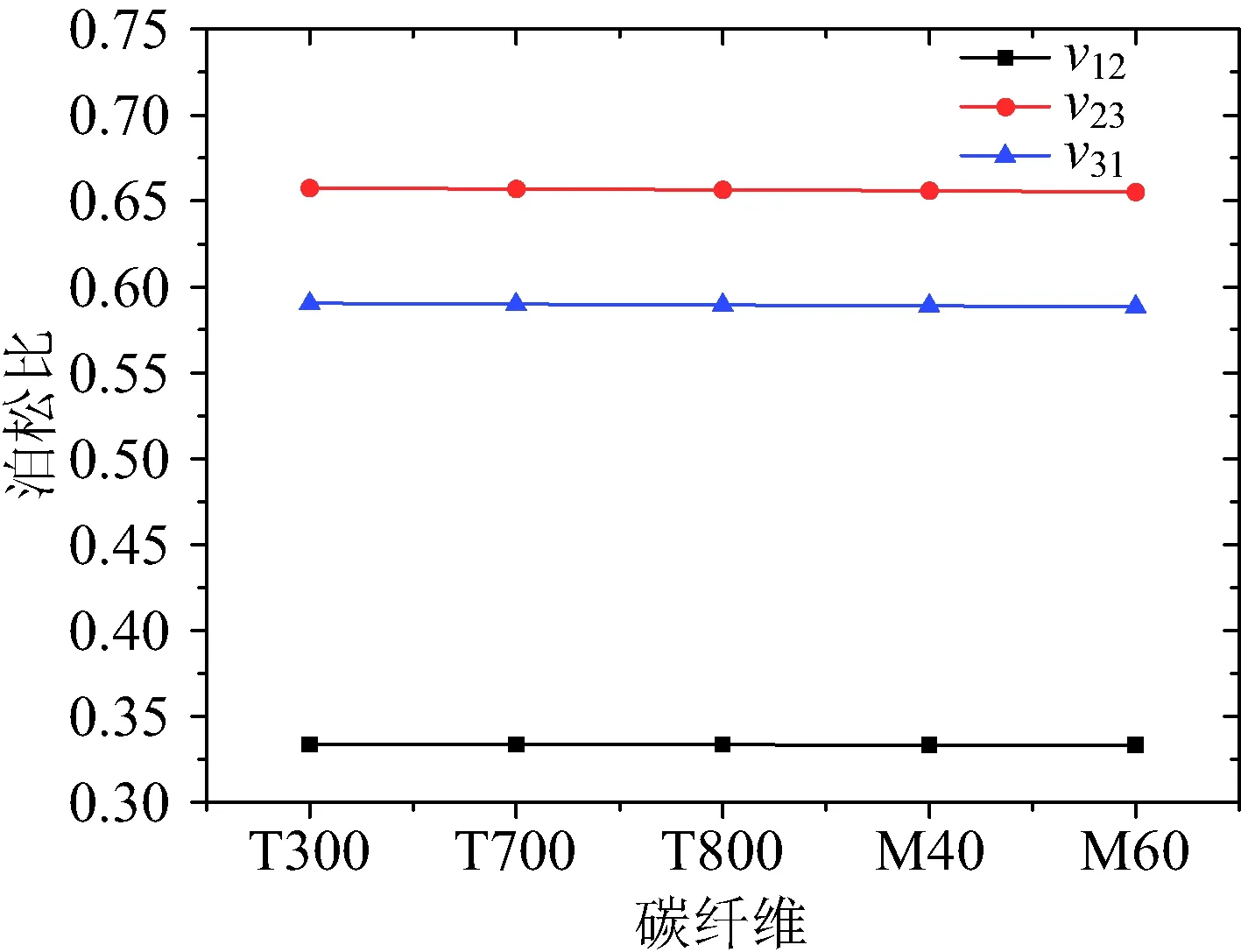
图17 碳纤维种类对泊松比的影响Fig.17 Effect of fiber types on Poisson′s ratio

4.2 纤维体积分数对单胞等效性能的影响

选择纤维体积分数Vf为40%、42%、45%和60%来讨论纤维体积分数变化对材料性能的影响。

图18～图20为拉伸模量E11，E22，E33随纤维体积分数Vf的变化规律，可以看到在相同的碳纤维下随着Vf增大，E11和E22均增大，而且随着碳纤维模量的增大，相同的ΔVf给E11和E22带来的增量越大；在Vf为40%～45%之间时，E33随着Vf的增大而减小，而当Vf为60%时，E33有一个跃增。

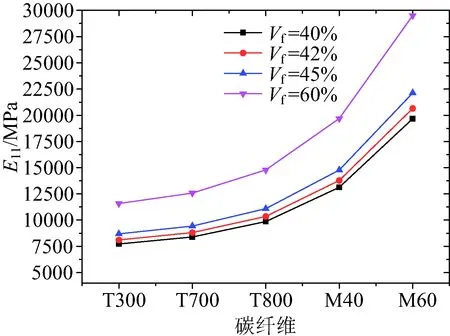
图18 纤维体积分数对面内拉伸模量E11的影响Fig.18 Effect of fiber volume content on E11

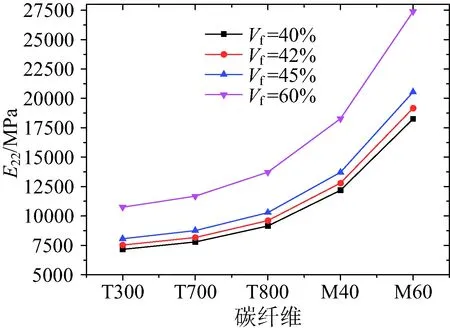
图19 纤维体积分数对面内拉伸模量E22的影响Fig.19 Effect of fiber volume content on E22

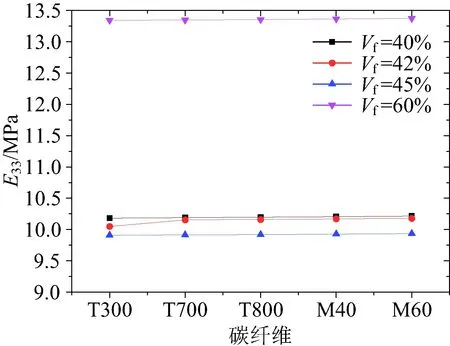
图20 纤维体积分数对面内拉伸模量E33的影响Fig.20 Effect of fiber volume content on E33

图21～图23为剪切模量G12，G23，G31随纤维体积分数Vf的变化规律，可以看到在相同的碳纤维下随着Vf增大，G12增大，而且随着碳纤维模量的增大，相同的ΔVf给G12带来的增量越大；在相同的碳纤维下随着Vf增大，G23和G31均增大。

图24～图26为泊松比v12，v23，v31随着纤维体积分数的变化规律，可以看到在相同的碳纤维下，随着Vf增大，v12是基本不变的，v23，v31略有减小。说明泊松比对纤维体积分数变化并不敏感。

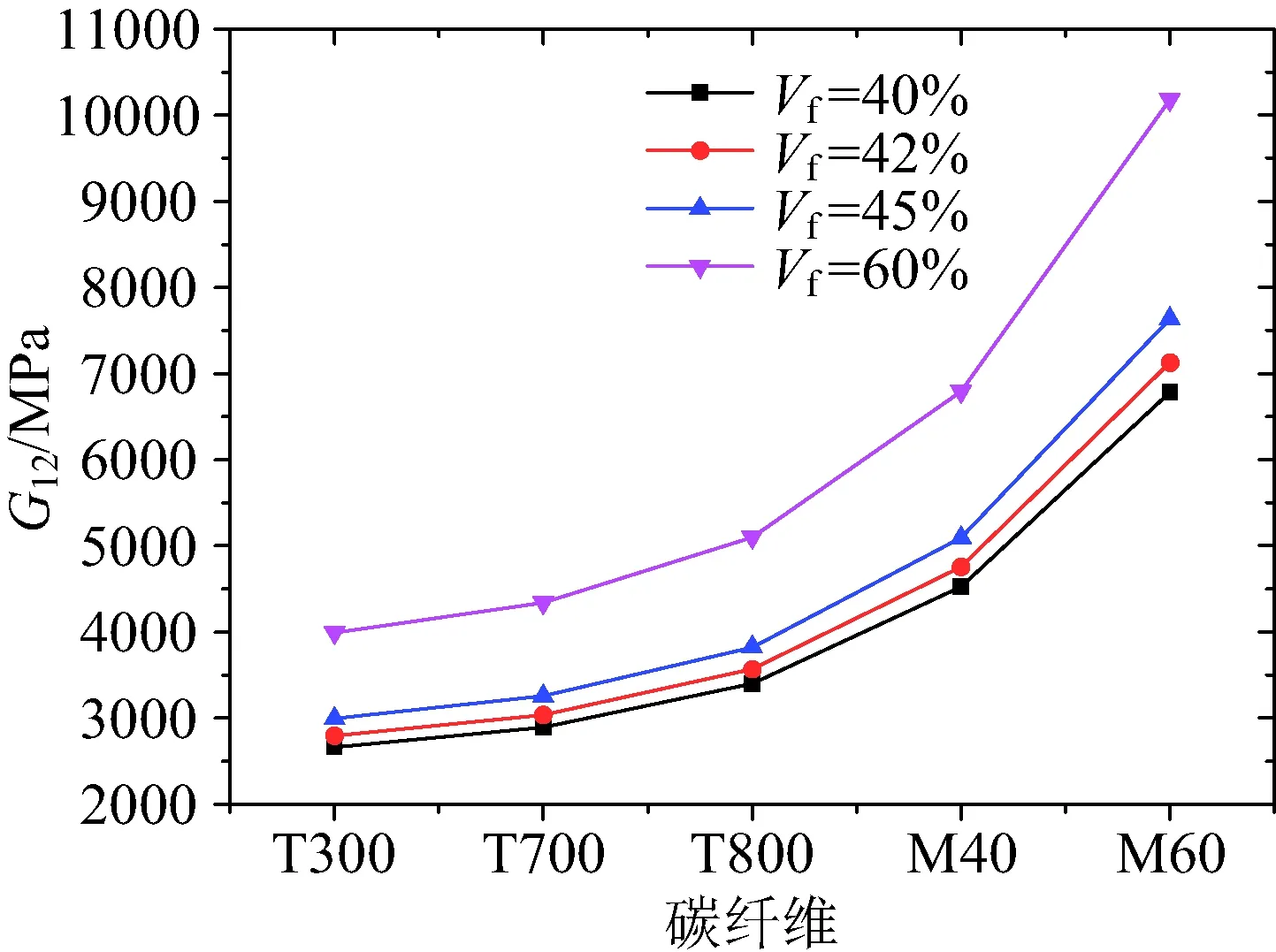
图21 纤维体积分数对面内剪切模量G12的影响Fig.21 Effect of fiber volume content on G12

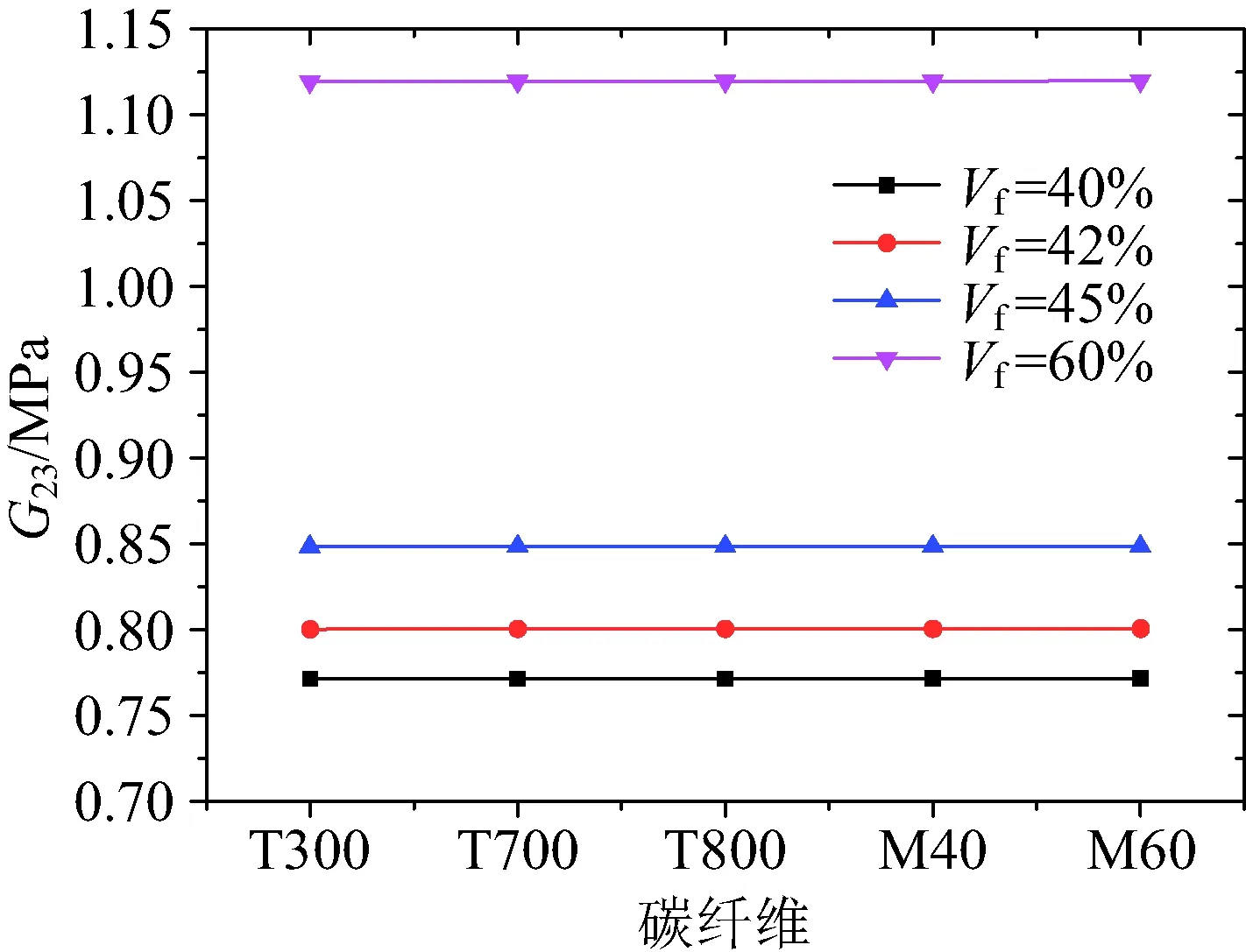
图22 纤维体积分数对面内剪切模量G23的影响Fig.22 Effect of fiber volume content on G23

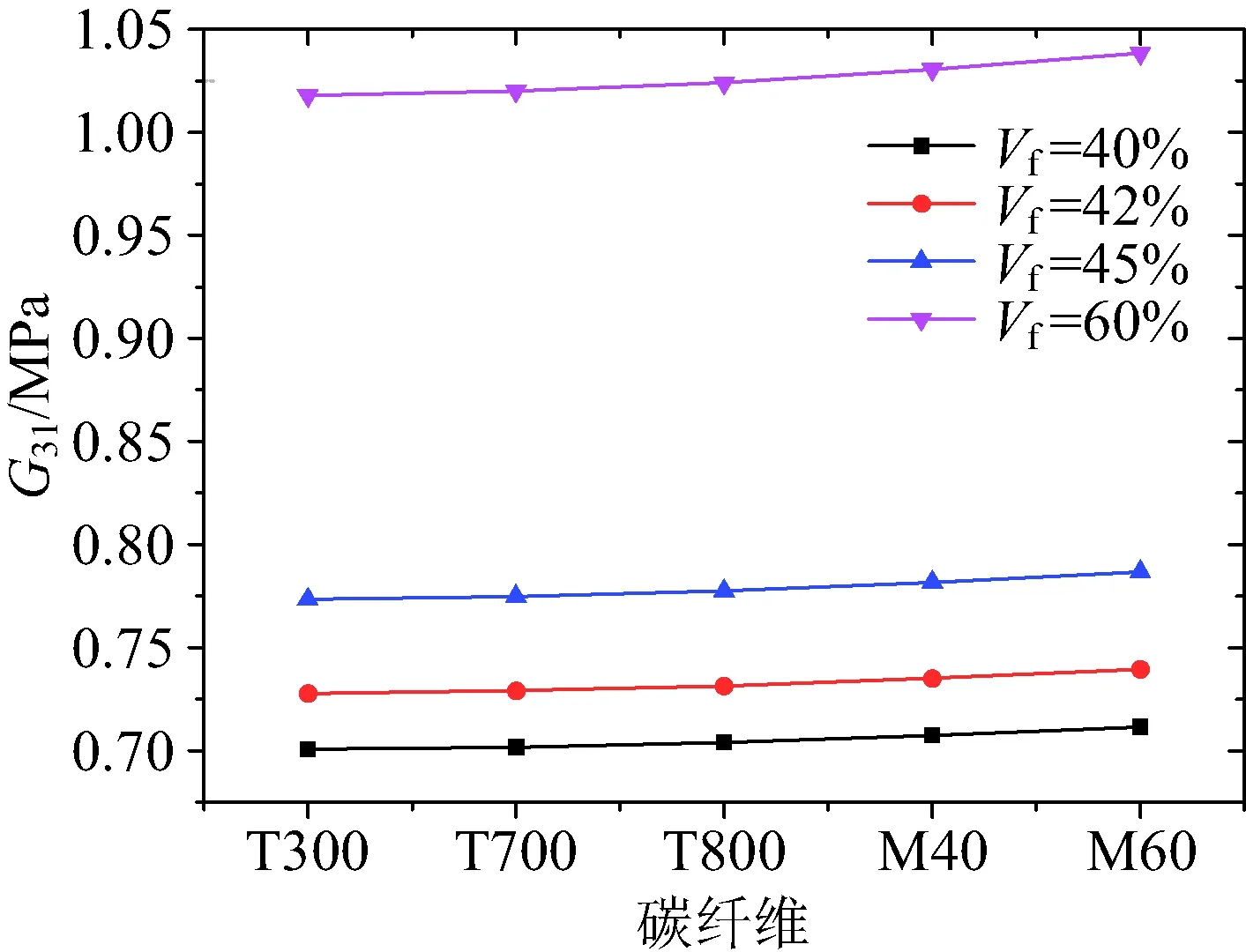
图23 纤维体积分数对面内剪切模量G31的影响Fig.23 Effect of fiber volume content on G31

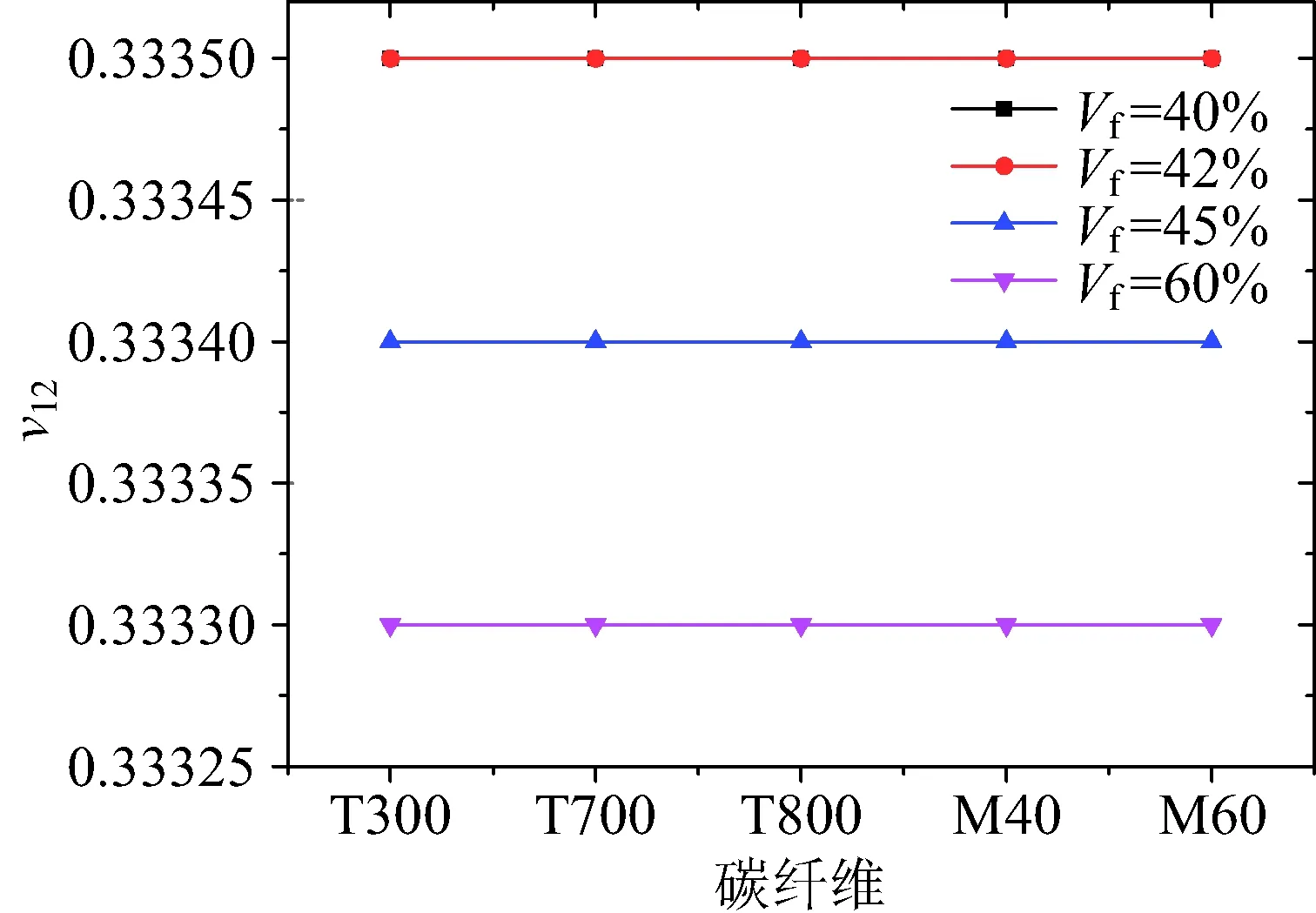
图24 纤维体积分数对面内剪切模量v12的影响Fig.24 Effect of fiber volume content on v12

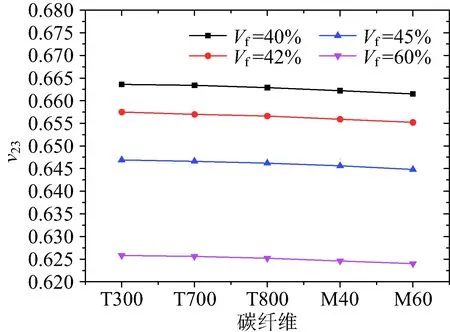
图25 纤维体积分数对面内剪切模量v23的影响Fig.25 Effect of fiber volume content on v23

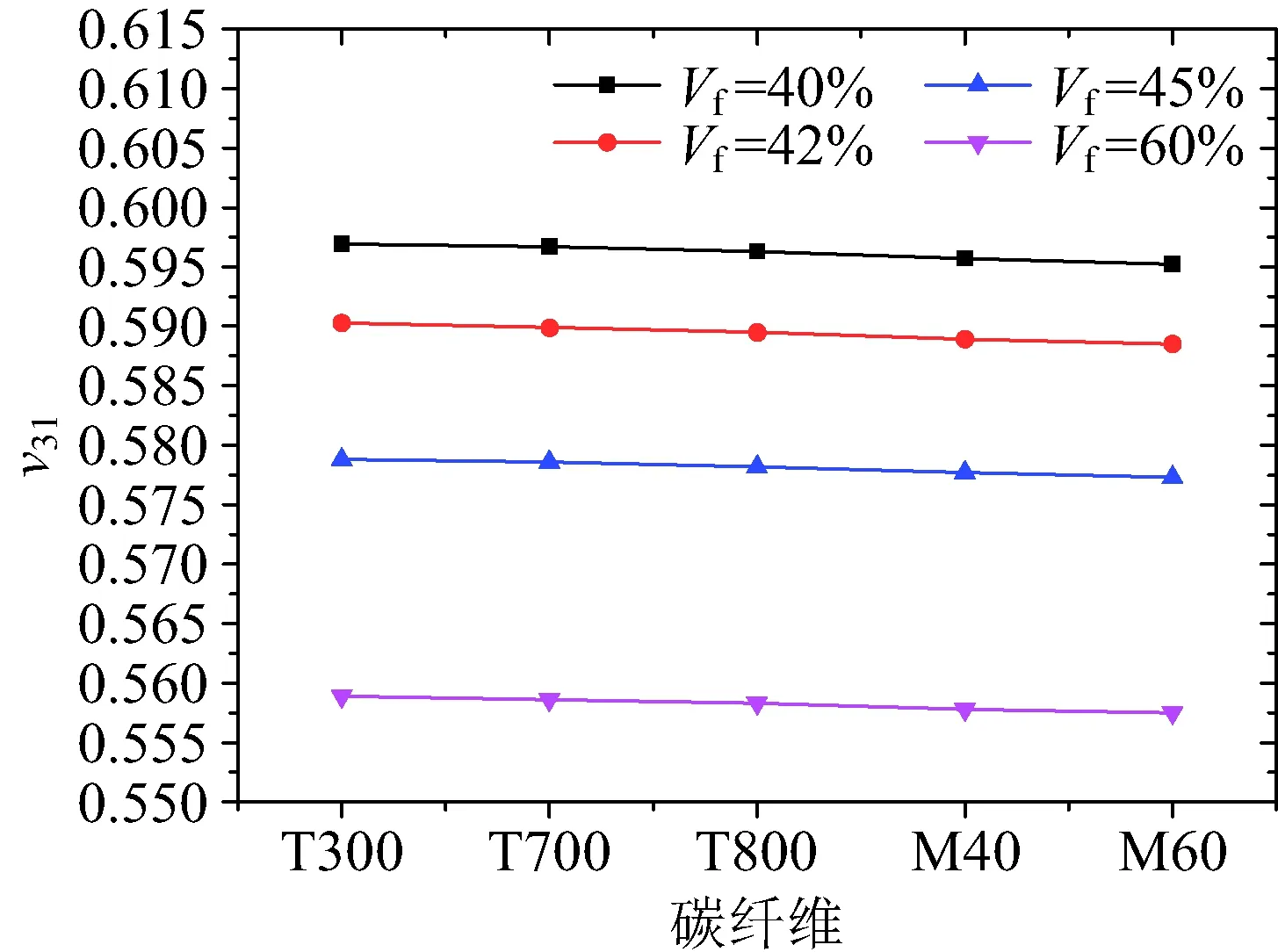
图26 纤维体积分数对面内剪切模量v31的影响Fig.26 Effect of fiber volume content on v31

5 结束语

采用复合材料细观力学的方法对硅橡胶基TWF复合材料进行了力学性能的分析。首先通过混合规则得到纤维束的材料特性(假设其为横观各向同性材料)；接下来选取合适的体积重复单元——单胞，考虑纤维束交叠情况，对纤维束波动情况进行了合理假设，建立了单胞实体有限元模型；在ABAQUS中对单胞有限元模型进行均匀化有限元分析，最终得到了TWF复合材料的等效力学特性。最后重点分析了碳纤维种类和纤维体积分数对于单胞等效性能的影响规律。随着碳纤维模量的增大，等效拉伸模量E11，E22，E33均增大，材料的面内各向异性更加明显；随着碳纤维模量的增大，等效面内剪切模量G12增大，横向剪切模量G23基本保持不变，G31呈缓慢增加的趋势。随着Vf增大，E11和E22均增大，随着碳纤维模量的增大，相同的ΔVf给E11和E22带来的增量越大；随着Vf增大，G12、G23和G31均增大，随着碳纤维模量的增大，相同的ΔVf给G12带来的增量越大；泊松比对于碳纤维种类以及纤维体积分数的变化并不敏感。该材料作为高精度天线反射器的反射面，需满足各项性能指标要求，主要包括刚度和可重复折叠性。本文研究的这两个参数对材料性能均有显著的影响，无论是碳纤维模量还是纤维体积分数的增大均可以使材料的刚度增大；但同样的材料的韧性会降低，对反射器折叠展开会带来不利的影响，因此在进行材料设计时需要综合考虑。