三维规则形貌影响下的二次电子发射特性研究
2020-06-23张娜崔万照曹猛王瑞胡天存
张娜,崔万照,*,曹猛,王瑞,,胡天存,
1. 中国空间技术研究院 西安分院 空间微波技术重点实验室,西安 710100 2. 西安交通大学 物理电子与器件教育部重点实验室,西安 710049
由电子辐照激发的二次电子发射现象一直以来都是物理电子学领域研究的基础和重点问题,其不仅是各类电子倍增管、扫描电子显微镜成像与检测、电子束探针微分析、俄歇电子能谱仪和其他电子表面分析仪器的核心原理[1-2],由其引发的二次电子倍增效应也是制约空间微波部件[3-5]、加速器[6-7]、高功率微波源[8-9]、核聚变等性能和可靠性的重要因素。特别是由二次电子发射引发的卫星有效载荷大功率微波部件的微放电效应,其一旦发生将导致谐振类设备失谐、噪声电平抬高、输出功率下降,甚至引发低气压放电,损坏微波部件表面,进而缩短微波部件寿命甚至造成微波部件永久性失效,最终影响通信信道乃至整个微波传输系统彻底失效。20世纪90年代以来,中国多颗卫星的微波部件在研制过程中发生了微放电问题,严重影响了航天器的研制进程。微放电问题已经成为制约中国航天器水平的瓶颈之一。随着中国航天技术的快速发展,导航卫星、通信卫星、遥感卫星等航天器的有效载荷朝着大功率、多通道、小型化、高可靠方向发展,微波部件承受的功率越来越高,体积越来越小,对微放电阈值的精确分析和提高也提出了更高的挑战。
从微放电效应形成的微观过程来看,它主要涉及两方面的过程:其一是电子与材料的相互作用过程,即二次电子发射过程;其二是电子在电磁场中的运动过程。这两个过程相互交替,相互影响。其中,描述二次电子发射过程的特性参量——二次电子产额(secondary electron yield, SEY)、二次电子能谱(secondary electron spectrum, SES)和出射角分布,分别决定了微放电形成过程中微波部件内运动的电子数目、电子从部件表面出射的初速度以及电子出射时的初始方向。因此,不管是对微放电微观过程精确仿真以期获得准确的微放电阈值,还是通过调控部件表面状态以实现对微放电的有效抑制,都需要掌握实际微波部件表面的二次电子发射特性。
由于规则表面形貌易于揭示形貌参量影响二次电子发射特性的内在机制及影响规律,而且采用光刻、等离子刻蚀等工艺可以较好地实现特定设计的规则形貌,因此在抑制微放电的研究初期或原理性试验验证过程中多采用定制的规则表面形貌。在微波部件中,通过定制表面形貌抑制微放电效应也已经受到越来越多的关注[10],叶鸣等[11]采用唯像概率模型计算了三角形沟槽、矩形沟槽、方孔及圆孔4种规则形貌的SEY。封国宝等[12]通过硅基材料的表面刻蚀和金属银表面溅射获得了圆柱孔和矩形槽等金属微陷阱结构,并测试和模拟了微陷阱结构的SEY。胡晶等[13]模拟了正方形、圆形、三角形凸起和凹陷结构的SEY。这些研究主要集中在表面形貌对SEY的影响,对于表面形貌下影响微放电出射电子能量和角度的SES和出射角分布尚未见报道。
本文首先介绍了表面形貌下的二次电子发射特性模拟方法,然后以三维表面形貌中的圆柱孔为例,介绍了深宽比、占空比等表面形貌参量对SEY、SES和出射角分布的影响规律,为有效抑制微放电和准确评估微放电效应提供参考。
1 二次电子发射模拟方法
蒙特卡罗(Monte Carlo,MC)模拟是研究电子与固体相互作用相关物理量最有力的理论方法[14]。它是一种使用随机数来进行各种物理计算和试验模拟的方法,可以被认为是一种理想的试验,对于研究电子在材料内部的散射过程非常适用。电子在固体内行进时,不可避免地会与固体内部的原子、分子发生碰撞,每一次碰撞都会引起电子损失能量和改变方向,这个过程称之为散射。散射可以分为弹性散射和非弹性散射。
弹性散射是电子与原子的碰撞,由于库仑相互作用的影响,电子将被原子核电势影响而改变运动方向。描述弹性散射重要的参数是弹性散射截面,凡是经过此散射截面的电子均会发生弹性散射。对于入射电子能量Ep<10 keV的情况,用量子力学分波法求解Schrödinger方程得到Mott弹性散射截面[15]在物理意义上更为严格。本文采用Penn提出的介电函数法[16]描述能量小于10 keV电子的非弹性散射过程。根据介电理论,介电函数ε(ΔP,ΔE)是介质对外部点电荷的响应。电子在金属材料中发生非弹性散射的微分散射截面是:
(1)
式中:λin为非弹性散射平均自由程;ΔE、ΔP分别为电子在非弹性散射中的能量损失、动量损失;a0为波尔半径;Im{-1/ε(ΔP,ΔE)}为能量损失函数,它决定了非弹性散射的概率、能量损失分布和散射角度分布。
对于表面为平面的金属材料,二次电子从材料内部出射后就不再返回,而当表面为非平面时,出射的二次电子则有可能再次与表面发生碰撞并进入材料内部,再次进入材料内部的电子与入射电子散射过程类似。电子照射到复杂表面形貌下的二次电子发射过程采用多代模型[17]进行处理,多代模型包含了两个核心过程:一是判断一定的出射电子是否会再次入射并计算其入射点,二是处理电子在表面出射和入射时运动状态的变化。
对于可以采用为数不多的几何结构参数来表征的规则形貌,在电子运动过程中,只需要计算电子在每次轨迹推进过程中所行走的线段是否与构成表面形貌的面相交。如果相交,则相交点即为电子出射的位置;如果不相交,则该电子此次轨迹推进不会出射,仍然采用MC方法计算其在材料中的下一次运动轨迹。具体计算流程如图1所示。
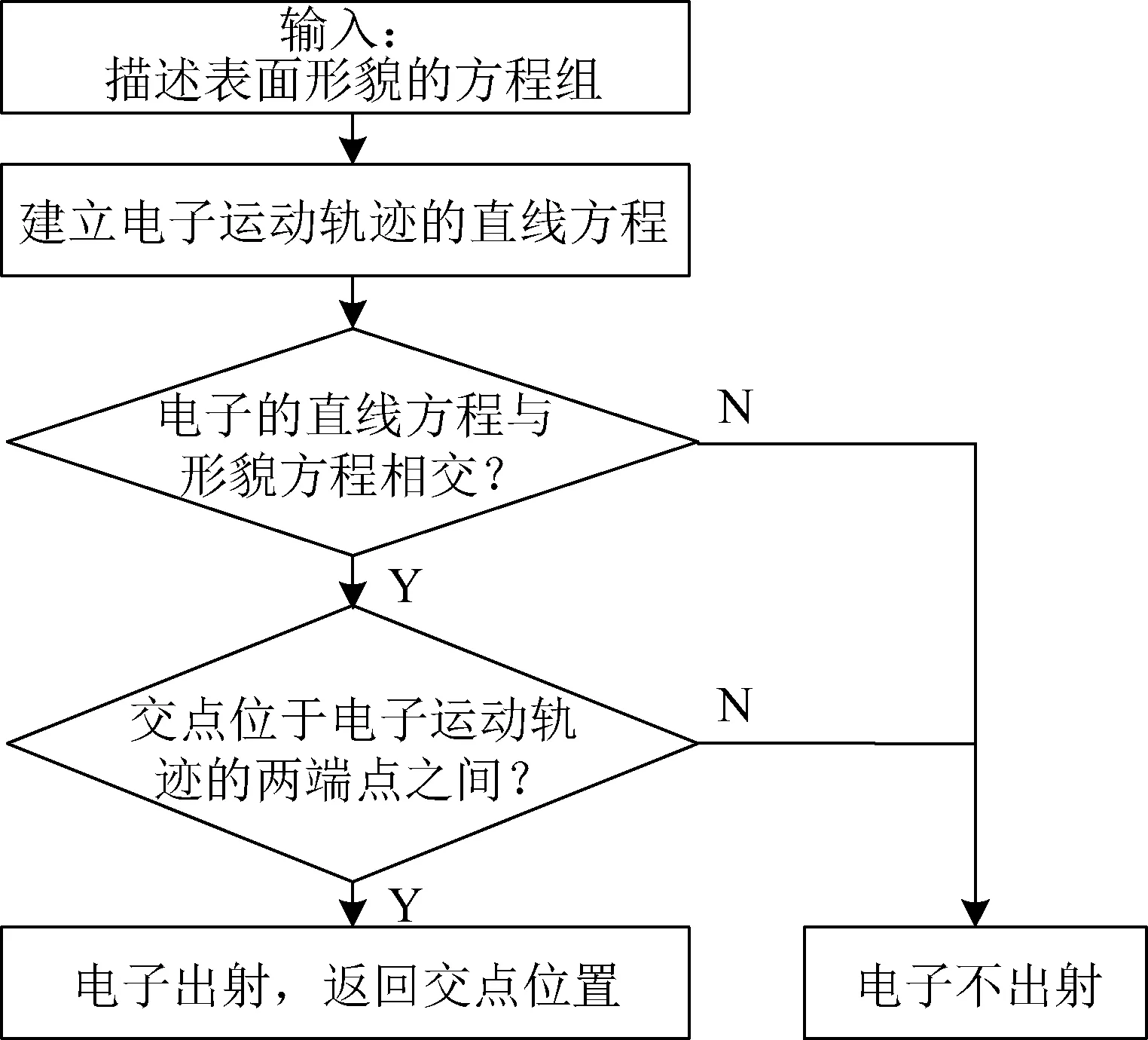
图1 电子从规则表面形貌出射判定流程Fig.1 Flow chart of ejection determination of electrons from regular surface morphology
电子在入射和出射具有表面形貌的表面时,由于不同入射点和出射点的表面法线方向可能不同,因而不同点的角度改变关系也不同。电子的出入射状态通过界面处的能量守恒和切向动量守恒进行修正。入射电子进入材料后的方向为:
(2)
电子出射材料后的方向为:
(3)
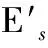
电子在固体中的散射过程由MC方法模拟,一旦二次电子从表面出射就判断其是否发生再入射。在电子入射和出射过程中,考虑电子与表面势垒的相互作用引起的电子能量和动量的改变,再入射电子的散射过程与初始入射电子过程相似。所有电子都被逐个追踪,直到其能量在材料内部耗尽,或者不再返回而形成最终出射的二次电子。出射电子的最终状态将构成有效的二次电子发射特性。
2 表面形貌的二次电子发射特性规律
图2给出了MC模拟时所用的圆柱孔的三维模型。图中虽然只给出了2×2的圆柱孔,实际仿真时的形貌为周期阵列结构。每个圆柱孔的形貌参数为:直径W、深度H。圆柱孔的占空比τ=πW2/(4L2),L为每个孔平均所占据的正方形边长。本文所有的MC模拟结果是以10万个电子均匀照射铜材料表面获得的,所形成的规律也适于其他金属材料的研究。
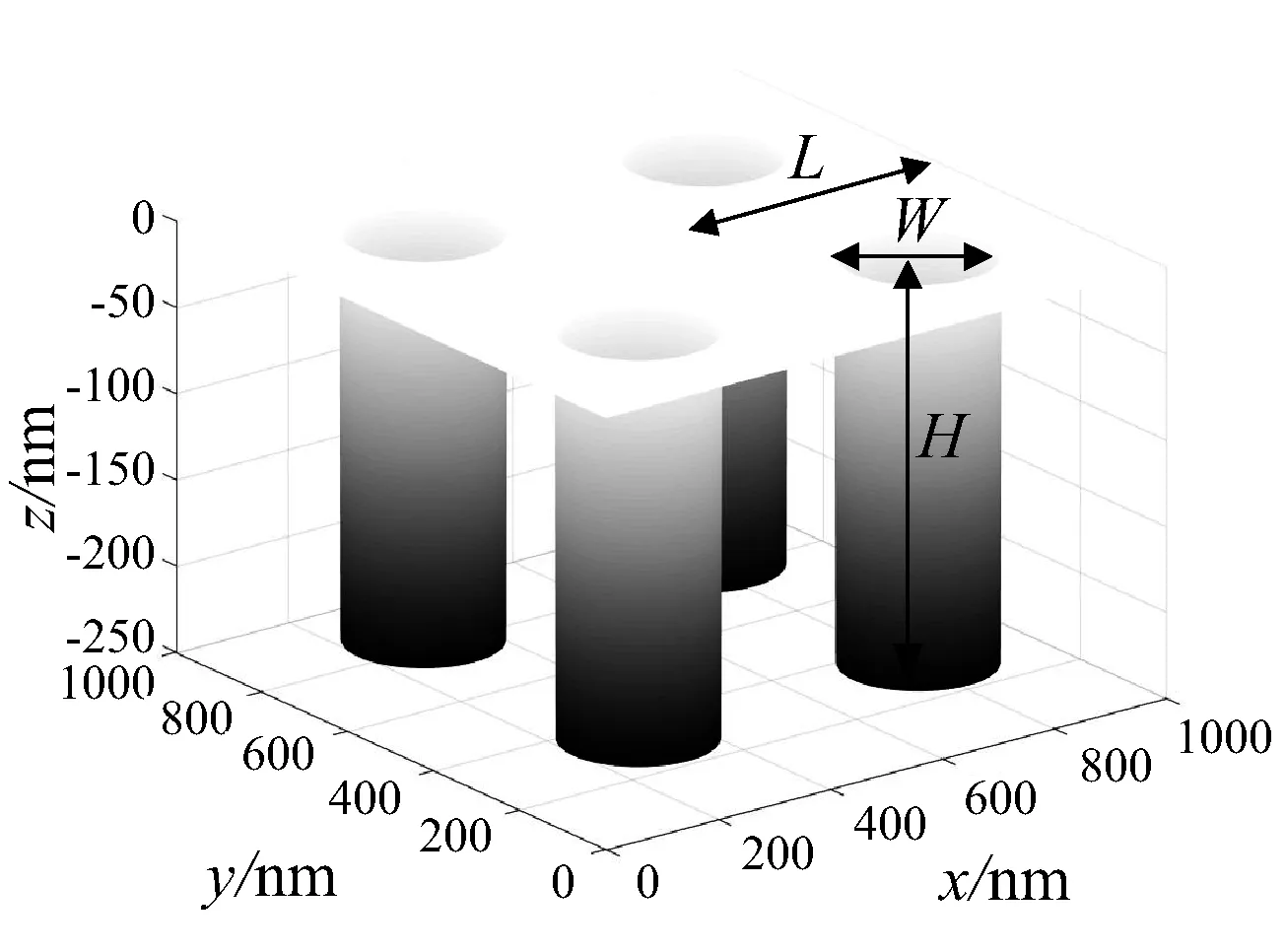
图2 圆柱孔的仿真模型Fig.2 Cylindrical hole model for simulation
首先,模拟了圆柱孔形貌下入射电子能量Ep对SEY的影响规律,如图3所示。图3(a)给出了占空比为0.5,H/W分别为0.25、0.5和1时,不同Ep下的SEY曲线。可以看出,圆柱孔的Ep与SEY的关系与光滑平面的规律相同,均是随着Ep增大,先增大后减小。但圆柱孔的SEY均小于光滑平面,这说明圆柱孔对二次电子具有抑制作用。此外,随着H/W增加,圆柱孔的遮挡效应增强,二次电子发射抑制效果增强,因而SEY降低。图3(b)给出了H/W=1,τ分别为0.3、0.5和0.7时,不同Ep下的SEY曲线。随着τ增加,圆柱孔所占比例增加,由于圆柱孔具有较好的抑制效果,因此SEY降低。
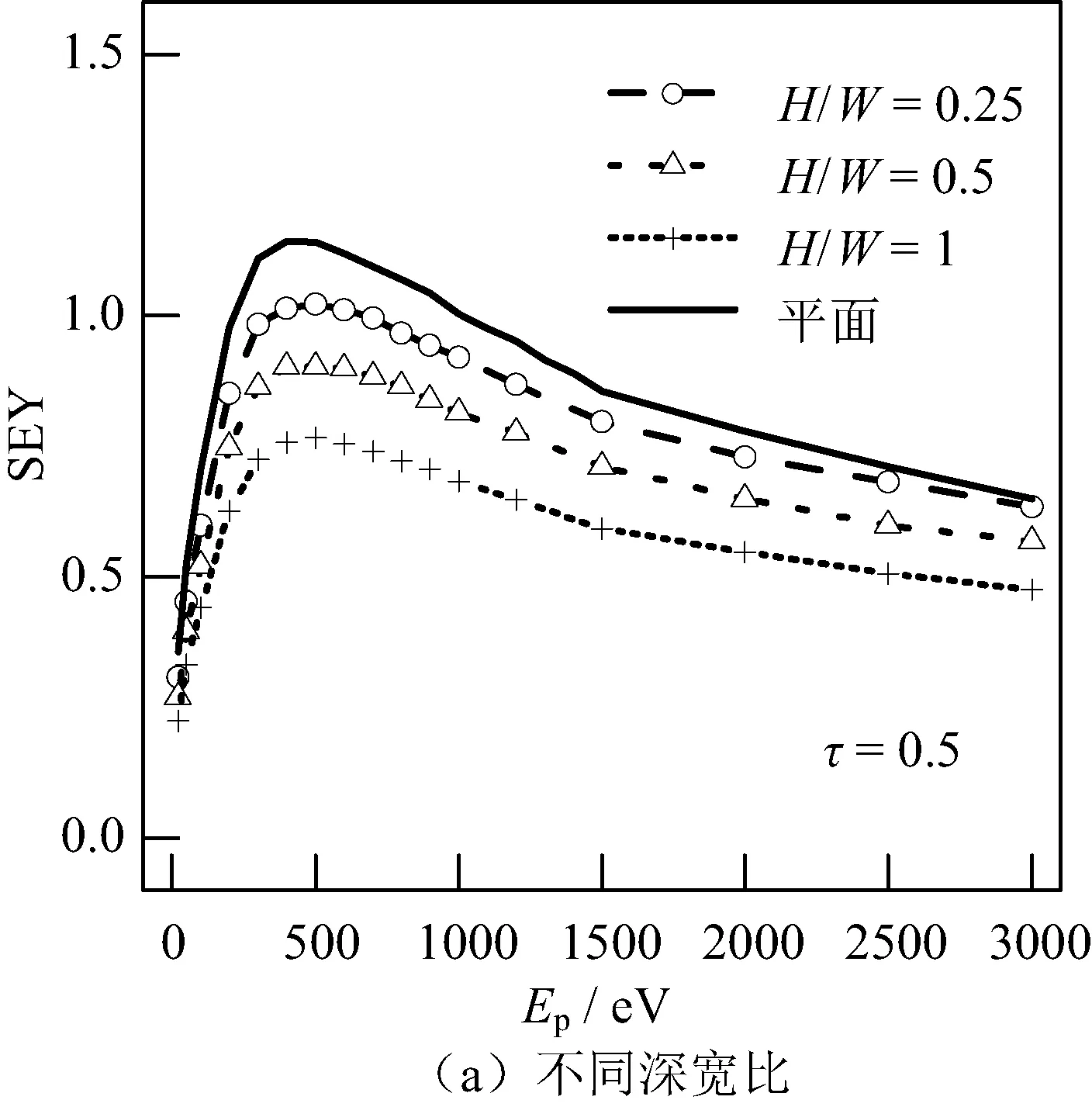
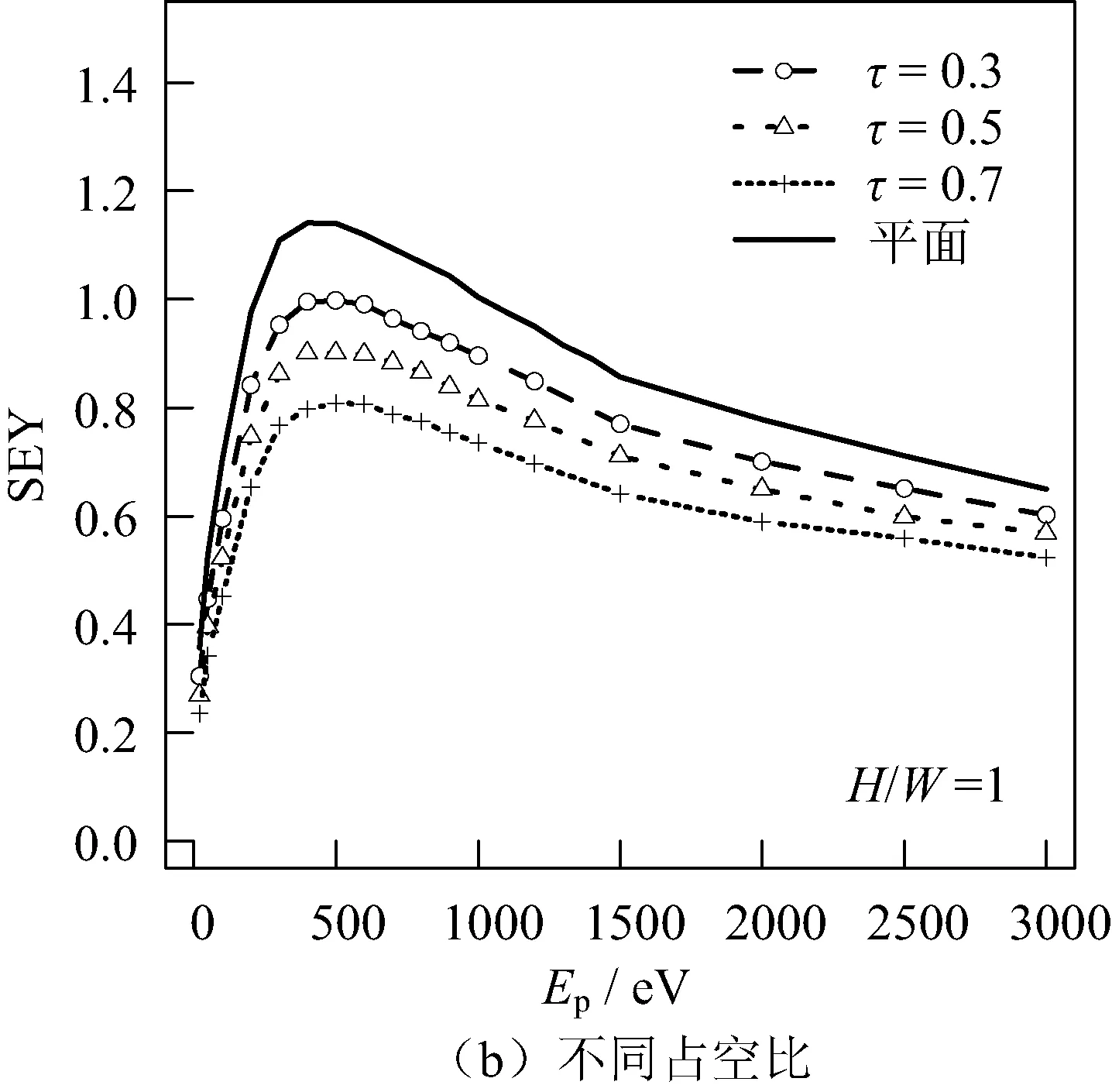
图3 圆柱孔Ep与SEY的关系Fig.3 Relationship between Ep and SEY of cylindrical hole
图4给出了圆柱孔的形貌参数影响SEY的规律。图4(a)是τ为0.5,SEY随着H/W的变化规律。从图中可以看出,Ep为100 eV、500 eV和1 000 eV时,随着H/W增大,SEY均在不断减小,说明增大H/W是抑制二次电子发射的手段。但是,当H/W增大到一定程度,SEY降低将非常缓慢,最后基本保持不变。这是由于被形貌遮挡的二次电子再入射材料内部会进一步产生新的二次电子,新产生的二次电子还可能继续再入射而产生更多的二次电子,形成多代效应。随着H/W增大,多代效应引起的二次电子增加与遮挡效应抑制的二次电子基本相当。因此,并非形貌的H/W越大越好,这不仅增加了表面形貌加工的难度,而且对于二次电子的抑制效果并不显著。
图4(b)给出了H/W为1,SEY随着τ的变化规律。从图中可以看出,随着τ增大,SEY先减小后增大。在τ较小时,三维圆柱孔比例增大,抑制效果增强,SEY增大。当占空比增大到一定值后,三维圆柱孔出现了反常增大。经过分析发现,当τ≥π/4时,相邻圆柱孔间相互交叠,起遮挡作用的圆柱壁消失,二次电子遮挡作用减弱。因此,当τ超过临界值时,随着τ增大,三维圆柱孔的SEY反而增大。
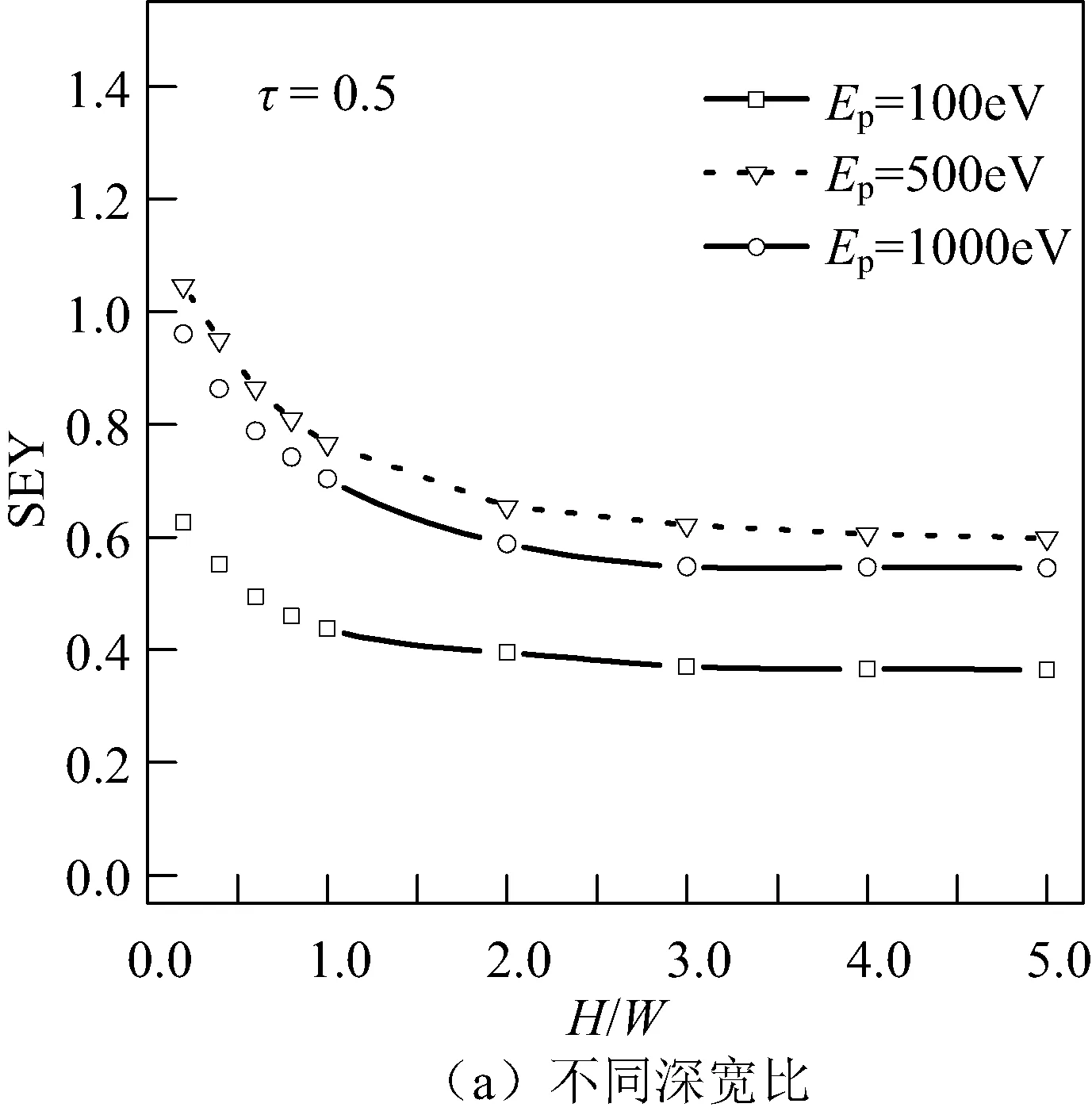
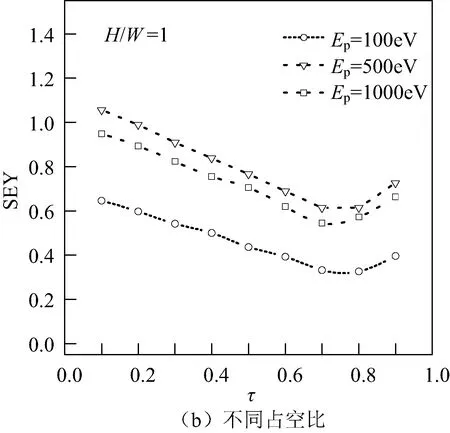
图4 圆柱孔的形貌参数影响SEY的规律Fig.4 Influence of morpholgoy parameter on SEY in cylindrical hole
下面研究三维圆柱孔形貌参量对能谱的影响规律。图5给出了电子均匀照射到三维圆柱孔内时,H/W分别为0.25、0.5和1时,Ep分别为100 eV和500 eV的归一化本征SES。其中,Es表示出射的二次电子能量,Ns表示出射的二次电子数目。为了便于比较,对各能谱以各自的最大值进行了归一化,(dNs/dEs)/(dNs/dEs)max表示归一化的二次电子数目。从图5中可以看出,Ep为100 eV时,不同H/W的归一化本征SES与平面基本重合,深宽比对本征SES的影响非常微弱。而Ep为500 eV时,多代效应增强导致本征SES展宽,并且随着H/W增大,多代电子占比越多,本征SES展宽越明显。
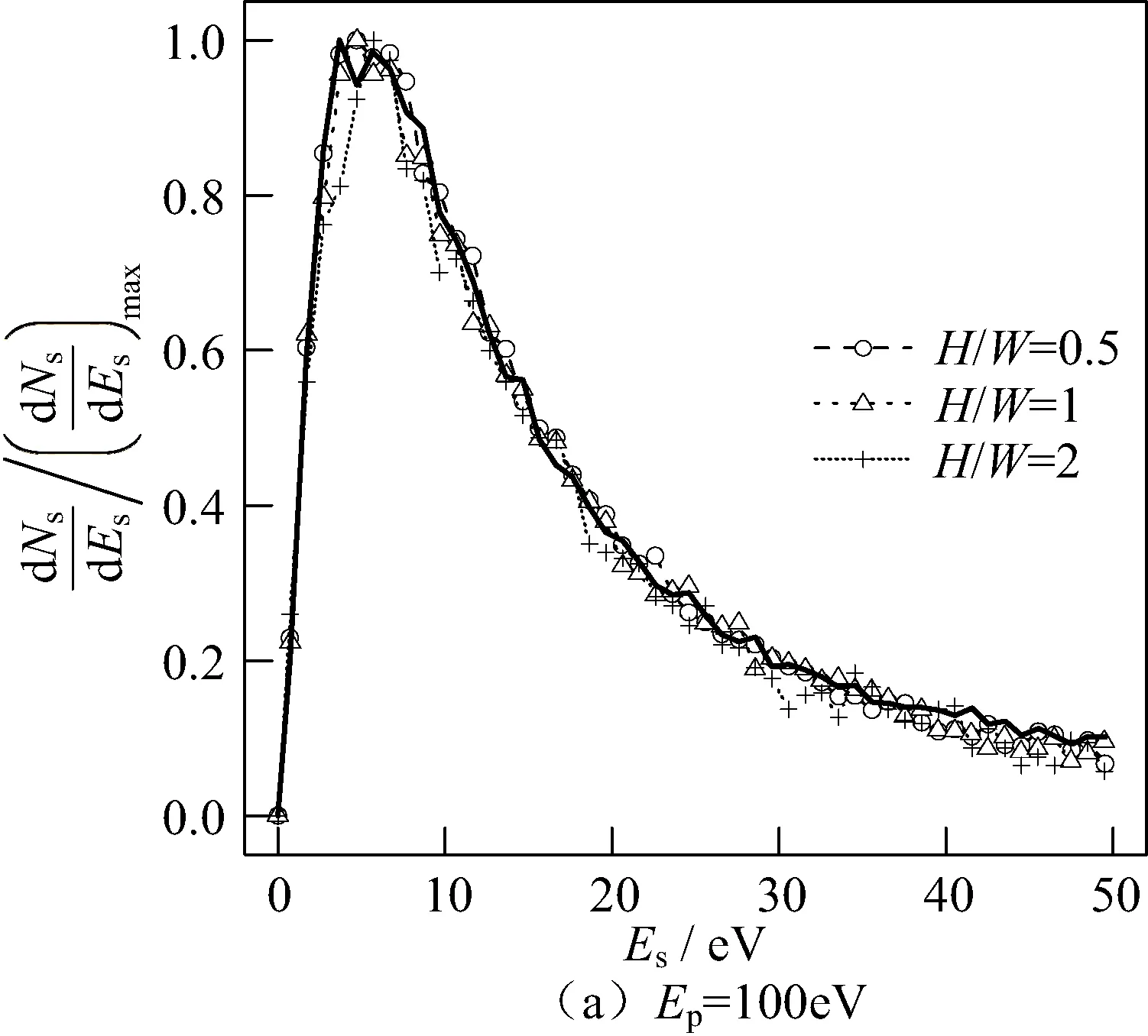
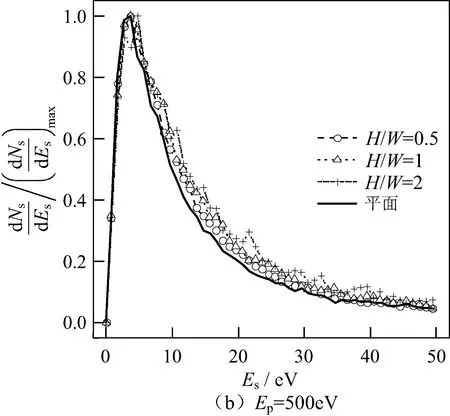
图5 圆柱孔的深宽比影响本征SES的规律Fig.5 Influence of H/W on ture SES in cylindrical hole
图6给出了圆柱孔的占空比影响归一化本征SES的规律,可以看出Ep为100 eV和500 eV时,τ对本征SES的影响均不明显。当Ep较小时,由于圆柱孔本身的本征SES基本没有展宽,因而100 eV下的圆柱孔本征SES与平面基本重合。当Ep较大时,圆柱孔内部出射的电子相对平面所占比例较小,因而圆柱孔略微展宽的本征SES也不再明显。
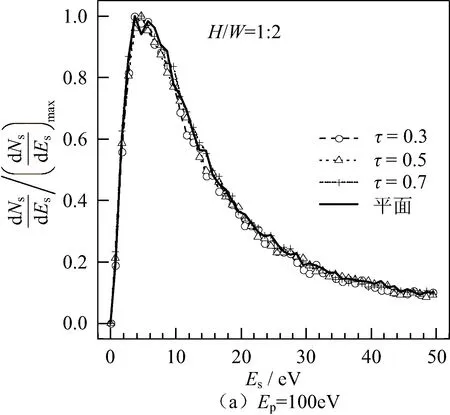
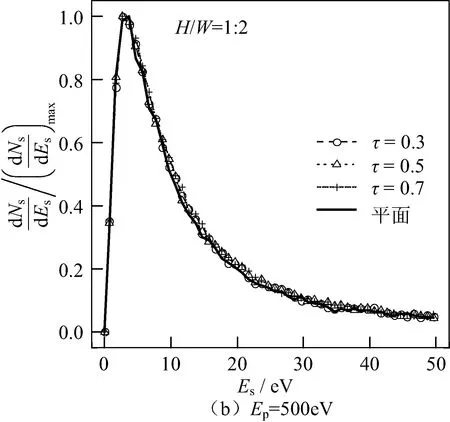
图6 圆柱孔的占空比影响本征SES的规律Fig.6 Influence of τ on ture SES in cylindrical hole
图7给出了不同形貌参数下三维圆柱孔的二次电子出射角度分布,Ep为500 eV,图中曲线上任一点与原点的距离代表了二次电子的相对数量,该点与原点的连线与y轴的夹角即为二次电子的出射角度。图7(a)给出了电子仅照射到圆柱孔内部时,H/W分别为0.25、0.5和1时的归一化二次电子出射角分布。为进行比较,同样给出了光滑平面的二次电子出射角分布,从图7(a)中可以看出,垂直材料表面方向的出射电子数目最多,由于三维圆柱孔对二次电子遮挡的角度选择作用,H/W越大,二次电子的出射角度越向法向方向集中。图7(b)表示H/W为0.5,不同τ的二次电子出射角分布。可以看出,τ越大,单位面积上的三维圆柱孔的数量越多,二次电子的出射方向越向法向集中;反之τ越小,平面占比越多,因而二次电子出射角分布越趋向于平面。
3 结束语
本文采用电子与复杂表面形貌相互作用的多代模型,以三维圆柱孔为例,系统研究了三维表面形貌对二次电子产额、二次电子能谱和二次电子出射角分布的影响规律,为全面评估表面形貌下的二次电子发射特性对微放电效应的影响规律提供了基础数据。通过研究得到以下结论:
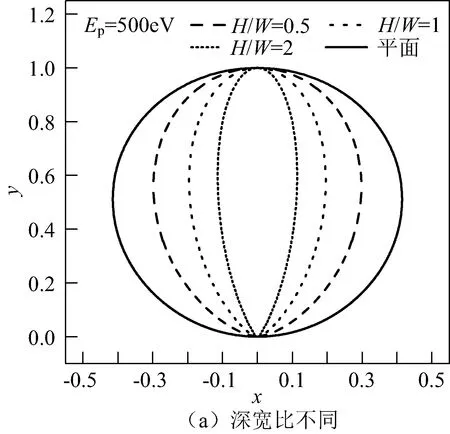
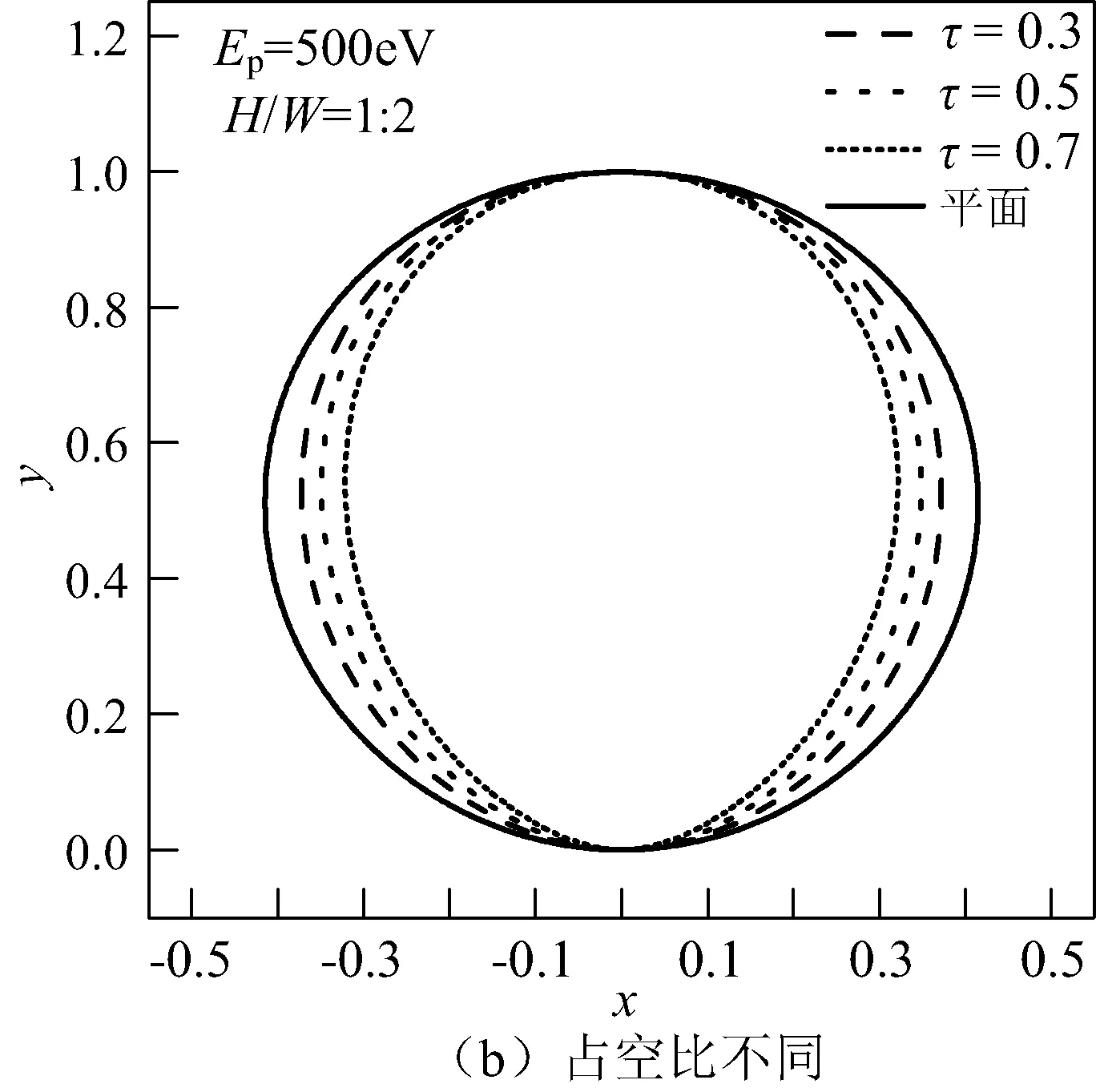
图7 圆柱孔不同形貌参数下的二次电子出射角度分布Fig.7 Distribution of secondary electron emission angle under different morphologic parameters of cylindrical hole
1)随着圆柱孔的深宽比增加,形貌遮挡作用增强,二次电子产额降低,但是由于多代效应的同步增强,深宽比对二次电子产额具有饱和作用。在形貌不发生交叠时,增加占空比能有效抑制二次电子发射。
2)深宽比增加时,入射能量越大,由多代效应引起的圆柱孔能谱展宽越明显,而电子均匀照射到具有一定占空比的表面时,由于圆柱孔的形貌遮挡作用导致出射电子所占比例较低,因而占空比对能谱的影响并不显著。
3)深宽比或占空比增大,二次电子出射角分布越向法线方向集中。
