二项式巧求解，多解法显身手——2017年浙江卷第13题解法探究

◇ 山东 刘艳美

涉及多项式的二项式问题是近年高考中比较常见的题型,其本质是依托二项式定理的定义、公式与性质,关键是把相应的问题加以合理地化归与转化,将其转化为易于求解的简单二项式定理问题进行求解,重点考查学生解题能力,培养学生数学核心素养.

1 高考真题

题目(2017年浙江卷)已知多项式(x+1)3·(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,则a4=________,a5=________.

分析1由于涉及的两个二项式的次数分别为3和2,次数不高,运算的量也不大,因此可以考虑直接利用多项式乘法来处理,比较直接有效.

解法1由于(x+1)3(x+2)2=(x3+3x2+3x+1)(x2+4x+4)=x5+(4x4+3x4)+(4x3+12x3+3x3)+(12x2+12x2+x2)+(12x+4x)+4=x5+7x4+19x3+25x2+16x+4,故a4=16,a5=4.

分析2将两个二项式各自展开,结合所求一次项的系数和常数项的值,通过两个乘式中项的性质加以分析与处理,可省去不必要的计算.

解法2由于(x+1)3(x+2)2=(x3+3x2+3x+1)(x2+4x+4),所以a4=3×4+1×4=16,a5=1×4=4.

分析3观察多项式的展开式,要求的两项分别是一次项的系数和常数项,可知其中常数项就是两个二项式的常数项相乘,而一次项的系数则是每个二项式的一次项系数与另一个二项式的常数项相乘的和.

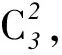
分析4先确定a4与a5所表示的意义,利用二项式定理通过分类讨论来确定含x项的系数a4,并直接通过特殊赋值法来求解常数项a5的值.

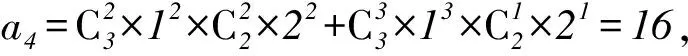
a5=(0+1)3(0+2)2=4.

本题主要考查二项式定理的运用,考查了化归与转化的数学思想和等价变形的能力.二项式定理是一个恒等式,可以结合二项式定理的定义加以展开,也可以根据系数特征进行处理,还可以利用特殊值加以赋值处理.方法众多,技巧各异.

2 变式探究

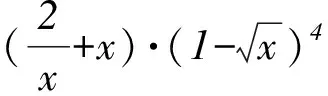
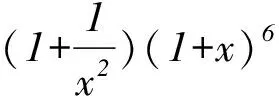
A. 15 B. 20 C. 30 D. 35

变式3已知多项式(x+1)4(x+2)3=x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7,则a1+a3+a5=________,a2+a4+a6=________.

①

令x=-1,可得-1+a1-a2+a3-a4+a5-a6+a7=(-1+1)4(-1+2)3=0,则有

a1-a2+a3-a4+a5-a6=-7,

②

由①+②可得a1+a3+a5=208,由①-②可得a2+a4+a6=215．

求解二项式系数问题,首先要掌握二项式定理的定义,熟记二项式系数的性质,其次要掌握特殊赋值法,赋值法是解决二项式系数问题的重要手段.