基于小波和MK检验的董志塬年降水量分析

2020-06-22赵双庆于宁宇

河北工程大学学报(自然科学版) 2020年1期

赵双庆，范文，于宁宇

(长安大学地质工程与测绘学院，陕西西安 710054)

董志塬是中国黄土高原区面积最大、保存最完整的黄土塬，但干旱和水土流失限制了该地区社会经济的可持续发展。董志塬地区以雨养农业，农业发展与降雨密切相关，降雨是当地农业生产的主要限制因素。引起水土流失最主要的外部动力因素是降水，由其引发的水土流失问题是黄土高原地区最严峻的环境问题，大面积的水土流失导致了土地资源的丧失和退化[1-4]。因此，研究董志塬区的降水时间分布及变化趋势，对于定量估算董志塬区区域土壤侵蚀量、预测未来降水变化趋势、合理安排农业生产以及科学制定水土保持措施具有重要的指导意义。降水在时间和空间上的分布规律及其对地表生态系统的影响是水文生态学研究的关键问题之一[5]。一直以来，降水规律都是国内外专家学者广泛关注的研究课题。Silva[6]使用MK方法对巴西东北部的气候变量的时间序列进行分析, 指出该地区的相对湿度和降水量呈下降趋势。Andreo等人[7]通过频谱分析、相关分析和连续小波分析研究了二十世纪以来伊比利亚半岛南部的气候和水文变化，指出该地区年平均降水存在5年的恒定周期，并预测整个21世纪该地区降水量呈下降趋势。左洪超等人[8]对中国近50年来降水量进行分析，表明我国年平均降水量没有明显的变化趋势但年降水量的变化存在着明显的区域特征。

不同地区降水变化的时间特征不同，对不同流域的降水时间特征进行评价仍然有很重要的价值，有很多专家学者应用MK检验和小波分析方法，研究了黄土高原地区降水量的趋势、周期、突变性等降水时间特征, 对黄土高原降水变化规律有了更深层次的认识[9-15]。目前，对黄土地区的降水规律研究大多是大范围整体性研究，对董志塬地区的降水规律研究较少，所以本文对该地区的年降水规律进行深入分析，将对董志塬的水土保持、生态建设以及灾害预防起到一定的指导意义。

1 研究区概况

董志塬位于甘肃省庆阳市中南部，北起驿马镇北部的桐川乡沿蔡家庙沟至庆城县一线，南止泾河谷底，东西介于马莲河与蒲河之间，地理坐标为N35.25—36.06,E107.46—107.96[16-18]。董志塬地区属于大陆性半干旱气候，降水分布不均匀，时有伏旱、暴雨、冰雹灾害；秋季降温迅速，潮湿多雨；冬季寒冷漫长，降雨稀少，年降雨量500～600 mm。泾河、马莲河、蒲河、黑河4条河流的373条一级支沟从四面八方伸向塬面腹地，塬区周边受冲沟切蚀呈树枝状，形成塬高谷深，沟壑纵横的陇东黄土塬侵蚀地貌。庆城县附近沟壑区侵蚀地貌见图1。董志塬区塬面和沟谷地层划分为：第四系全新世Q4(冲积土层)、晚更新世Q3(马兰黄土)、中更新世Q2(离石黄土)、早更新世Q1(午城黄土)、上、中新世N2(蓝田组红粘土)，工程地质图见图2。

图1 董志塬上的沟壑地形Fig.1 The gulliesofthe Dongzhi Tableland

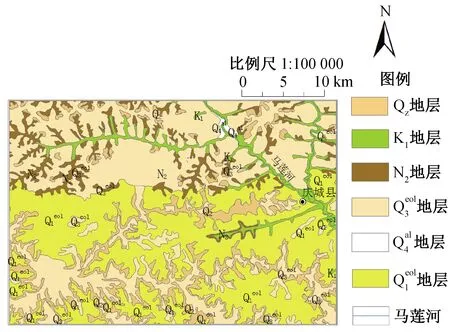
图2 董志塬北部研究区工程地质图Fig.2 The engineering geological map of the research area in northern of the Dongzhi Tableland

2 数据来源与研究方法

2.1 数据来源

本文降水资料来源于中国气象局董志塬区内的西峰站点及南部附近的长武站点1959—2016年的逐日监测数据。气象监测站点位置，见图3。为了得到董志塬的降雨变化的总体趋势，将各站日降雨量累计，得到1959—2016年各年的年降雨数据。

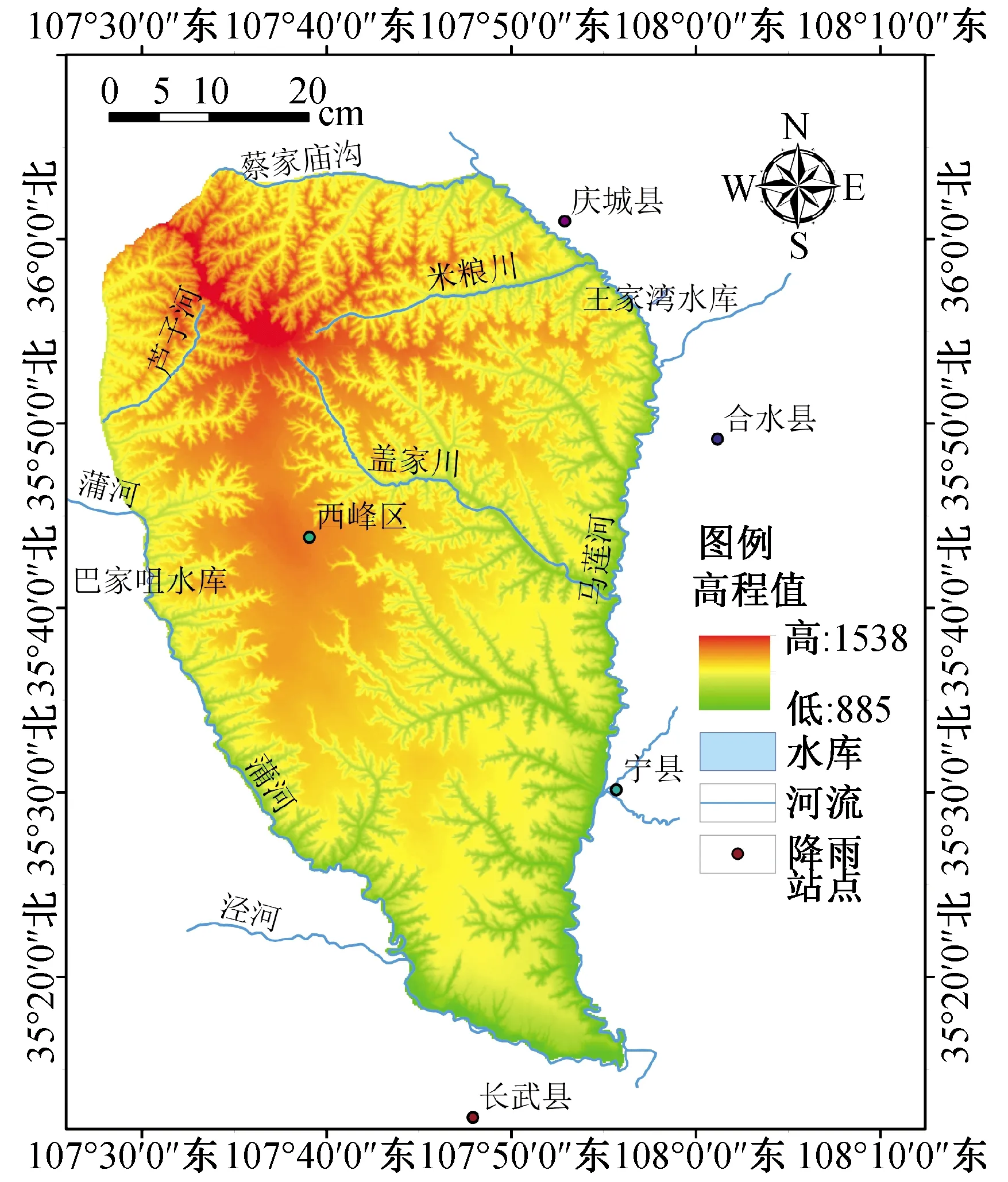
图3 董志塬数字高程模型及气象站的位置Fig.3 The numerical elevation model and location of weather station in the Dongzhi Tableland

为了保证数据质量，本研究仅使用中国气候参考网(CCRN)的数据。由中国气象局管理的CCRN由最先进的站点组成，这些站点配备了高质量的仪器，并遵循严格的观测协议，特别是用于检测气候变化信号[19]。

2.2 Mann-Kendall检验法

本文采用MK检验方法来分析董志塬降水站点的年降水量,得到董志塬地区年降水量变化趋势以及降水量突变年份，具体分析方法简述如下。

2.2.1 MK趋势检验

(1)构建董志塬降水站点的年降水量时间序列(x1，x2，…，xn)，假设H0表示该时间序列中的数据是独立的，随机变量同分布的样本，没有线性变化趋势。

(2)计算检验的统计变量S:

(1)

(3)对于有10个或者更多数据点的时间序列，使用正态近似。统计值S的方差计算如下：

(2)

其中年降水量相同的样本的个数记为i，i值相同的样本中降水量不同的样本的个数记为ei。

(4)构造的标准正态分布变量Z计算如下式：

(3)

(5)在一定的α置信水平上,如果Z≥|Z1-α/2|则拒绝原假设,即在α置信水平上, 年降水量时间序列存在明显的趋势。

(6)其变化趋势的大小用β表示,计算如下：

(4)

若β>0，表示呈上升趋势；若β<0，表示呈下降趋势。

2.2.2 MK突变检验

根据董志塬降水站点的年降水量时间序列(x1，x2，…，xn)，然后我们构造一秩序列：

(5)

其中

(6)

定义统计量：

(7)

其中，sk的均值和方差分别为E(sk)，var(sk)，时间序列独立同分布的情况下，它们的表达式如下：

(8)

把时间序列x逆序排列xn，xn-1，…，x1，再通过(7)式求出UFk，同时令UBk=-UFk(k=n，n-1，…，1)，UB1=0。得到的统计序列UFk和UBk，UFk的正负表明xk的变化趋势，正值表明序列呈上升趋势，负值表明呈下降趋势；当UFk和UBk超过显著性临界直线时，说明趋势显著。UFk和UBk曲线的交点如果在临界线之间，则交点对应的时刻为突变发生的时间[20]。

2.3 Morlet小波分析

在分析时间序列时，需要获得平滑连续的小波振幅以及时间序列的振幅和相位的信息，因而选择非正交的复值小波。Morlet小波是非正交性的复值小波，因此国内外专家学者大多采用Morlet小波对气象时间序列进行周期分析[21]。曹晓敏等[9]应用小波分析，得出黄土高原中部降雨量具有2～3 a和7 a左右的年际振荡，其中以2～3 a的年际振荡尤为明显。郝立生等[21]通过Morlet小波分析发现，太阳活动存在14.5 a的显著周期。李淼等[23]采用Morlet小波函数，对该地区近300 a 来降水的年际变化时间序列进行了小波分析，得出该地区年降水量时间序列存在21 a、35 a 和85 a 左右的主周期，并指出85 a 周期是第一主周期。本研究采用气象学分析时间序列常用的Morlet小波函数，对董志塬降水站点的降水时序进行分析，并用红噪声或白噪声标准谱对小波功率谱的显著性进行检验，从而得到董志塬年降水量周期性变化规律。

Morlet小波函数及离散小波变换公式为：

φ(t)=π-1/4e-t2/2eiabt

(9)

(10)

式中，ω0是角频率，Torrence等人认为取6比较合适[21-22],ωf(a,b)为小波变换后的小波系数，f(iδt)为进行分析的降水时间序列，δt为时间序列的时间间隔；ωf(a,b)为卷积后的小波系数，a和b分别为尺度因子(表示小波的周期长度)和平移因子(表示时间上的平移)，“*”表示复共轭。本文对年降水量进行分析，降水时序的时间间隔为1年，δt取1。

小波功率谱Ea,b定义为：

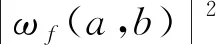
(11)

小波功率谱的显著性检验一般应用红噪声或白噪声标准谱来实现。求得降水时间序列滞后1的自相关系数r(1)，如果大于0.1则用红噪声谱进行检验，若小于0.1，则令r(1)=0，用白噪声谱进行检测。Torrence[21]指出小波功率谱服从χ2分布。在一定的显著水平上，计算得到红噪声或白噪声的显著性理论谱P。如果理论谱小于小波功率谱，则说明这种尺度对应的周期具有显著性。

理论功率谱：

(12)

Pa为红噪声或白噪声谱：

(13)

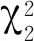
若Ea,b>P，说明小波功率谱是显著的。

3 结果与分析

3.1 年降水量变化趋势分析

通过前述方法得到的西峰、长武站点MK趋势检验统计参数见表1、表2；西峰、长武站点年降水量随年份的变化趋势线见图4、图5。

表1 西峰站点MK趋势检验统计参数

表2 长武站点MK趋势检验统计参数

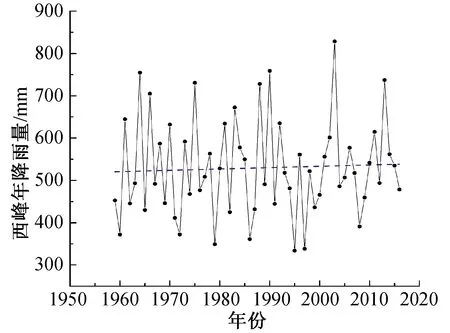
图4 西峰站点年降水量时序及变化趋势线Fig.4 The timing and the trend line of annual precipitation at Xifeng station

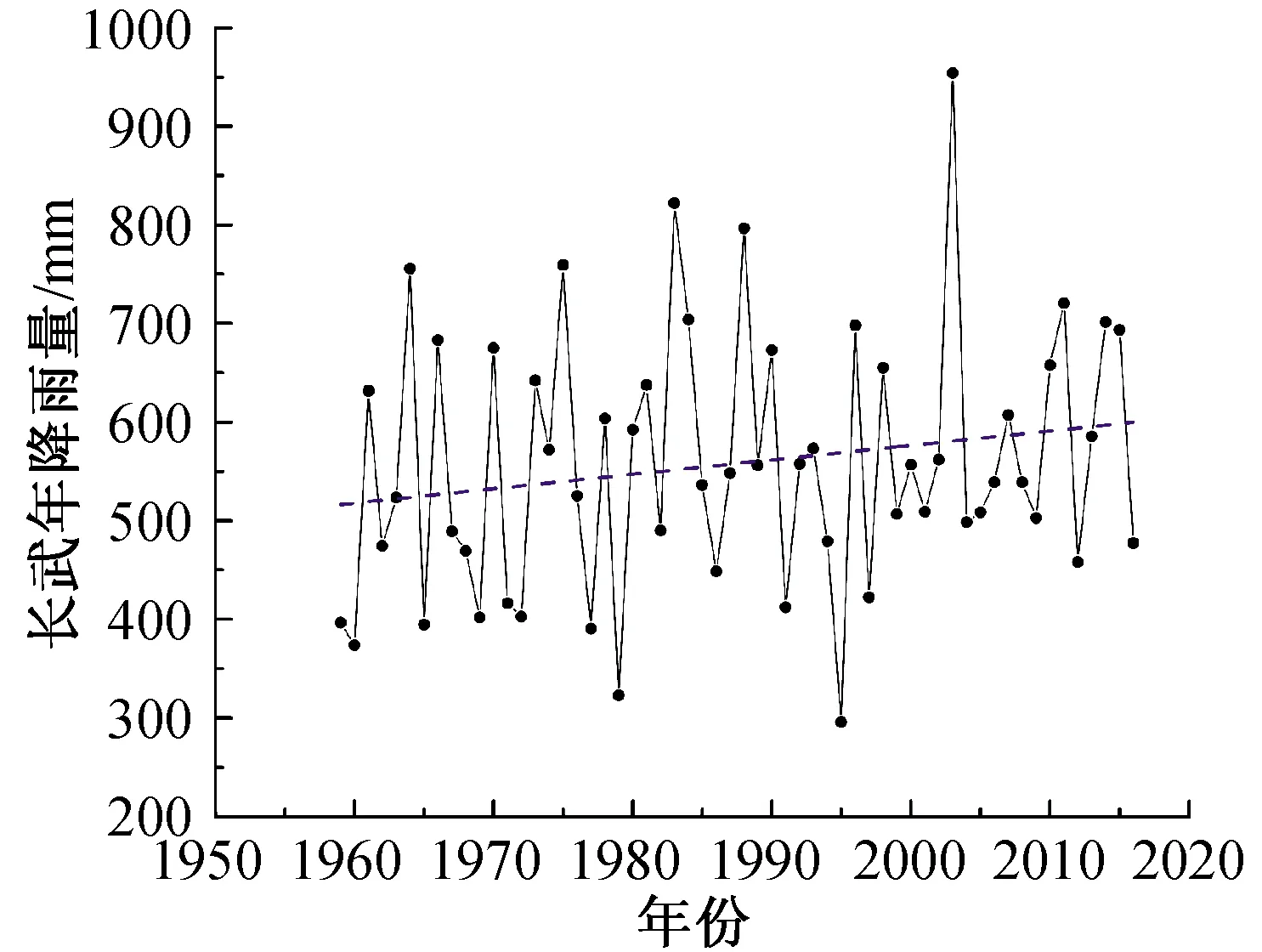
图5 长武站点年降水量时序及变化趋势线Fig.5 The timing and the trend line of annual precipitation at Changwu station

应用MK检验法检验分析水文时间序列时，在0.05的显著性水平下，Z≥|Z1-α/2|拒绝原假设具有统计学意义。显著性水平α取0.05时，拒绝原假设说明存在显著的变化趋势；显著性水平α取0.01时，拒绝原假设说明存在非常显著的变化趋势[24]。

西峰站点，MK分析中位数β=0.553>0，年降水量变化成上升趋势，上升幅度为5.53 mm/10 a，西峰站点年降水的Mann-Kendall趋势检验值Z=0.550<1.96，未通过置信度95 %的显著性趋势检验，西峰站点年降水量呈上升趋势，但未表现出显著性特点。长武站点，MK分析中位数β=1.42>0，年降水量的变化成上升趋势，上升幅度为14.2 mm/10 a，长武站点年降水的Mann-Kendall趋势检验值Z=1.542<1.96，未通过置信度95 %的显著性趋势检验，长武站点年降水量呈上升趋势，趋势不显著。

综上分析，董志塬地区1959—2016年年降水量呈不显著上升趋势，年降水量以5.54～14.2 mm/10 a的速率增加。

3.2 MK突变检验结果与分析

通过前述MK突变检验方法，绘出的UFk和UBk曲线图如下：

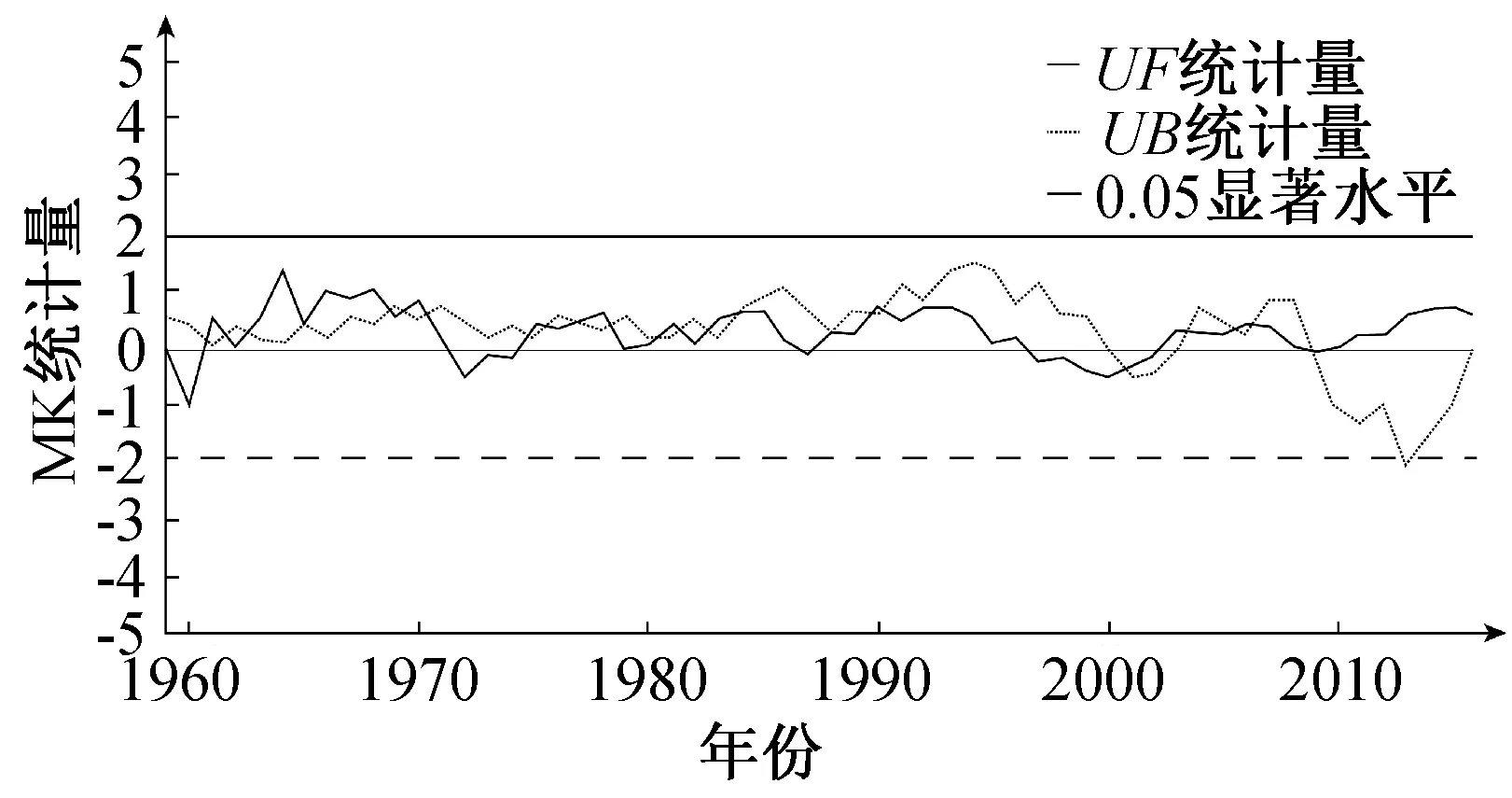
图6 西峰站点年降水量MK统计曲线图Fig.6 The MK statistical curve of annual precipitation at Xifeng station

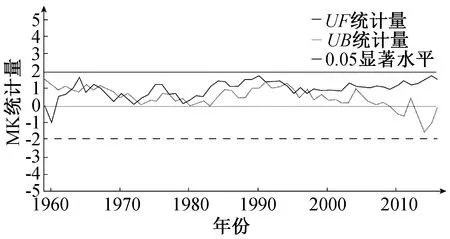
图7 长武站点年降水量MK统计曲线Fig.7 The MK statistical curve of annual precipitation at Changwu station

从西峰站点年降雨量MK检验的UFk趋势线中可以清晰看出，20世纪年降水量变化趋势：20世纪60年代初期下降，然后上升，到70年代初呈下降趋势，70年代后至90年代初一直呈现上升趋势，90年代末至00年代初呈下降趋势，之后又呈现上升趋势。从UFk和UBk的交点可以看出年降水量突变现象，降水量突变年份分别为1962年、1970年、1985年、2003年、2009年。从长武站点年降水量MK检验的UFk趋势线中可以清晰看出，20世纪60年代后，长武年降水量一直处于上升趋势。从UFk和UBk的交点可以看出年降水量突变现象发生在1963年、1971年、1979年、1995年。

综上得出，董志塬降水量突变起始年份分别为1962年、1970年、1985年、1995年、2003年、2009年。最小与最大降水的年份为1995年、2003年，这正好与年降水量突变起始年份1995年与2003年相对应。

3.3 小波分析结果

应用Morlet小波对董志塬气象站点年降水时序进行小波分析，其中年降水时序小波功率谱中的黑色实线为影响锥(COI)，COI考虑了小波函数与信号两端数据卷积所产生的计算结果影响范围，其内部为可信分析结果。黑色虚线内则为显著性90%的功率谱。小波系数实部时频分布图可以得到降水时序的时间、频率变化特征。在时间尺度一定的情况下，降水量在该尺度下的变化特征通过小波系数实部随时间的变化来反映。正值对应降水量偏多的情况，负值对应降水量偏少的情况。年降水量时间序列的主要时间尺度(主周期)，可以通过降水时序小波功率谱来确定。

3.3.1 西峰年降水量的小波分析结果

西峰的情况如图8及图9所示，可见其存在三种时间尺度变化周期，分别为1～2年、7～8年、9～14年时间尺度。从图9可以看出，影响锥内的可信分析结果，时间尺度7～8年在能量上占了主要部分，是影响未来该地区降水量的主要时间尺度，该时间尺度在20世纪80年代趋势比较明显，震荡中心显示其枯水与丰水期的交替周期约为8年。而1～2年的周期主要存在于20世纪60年代早期一段时间，9～14年的周期主要存在于20世纪80年代末至90年代末。

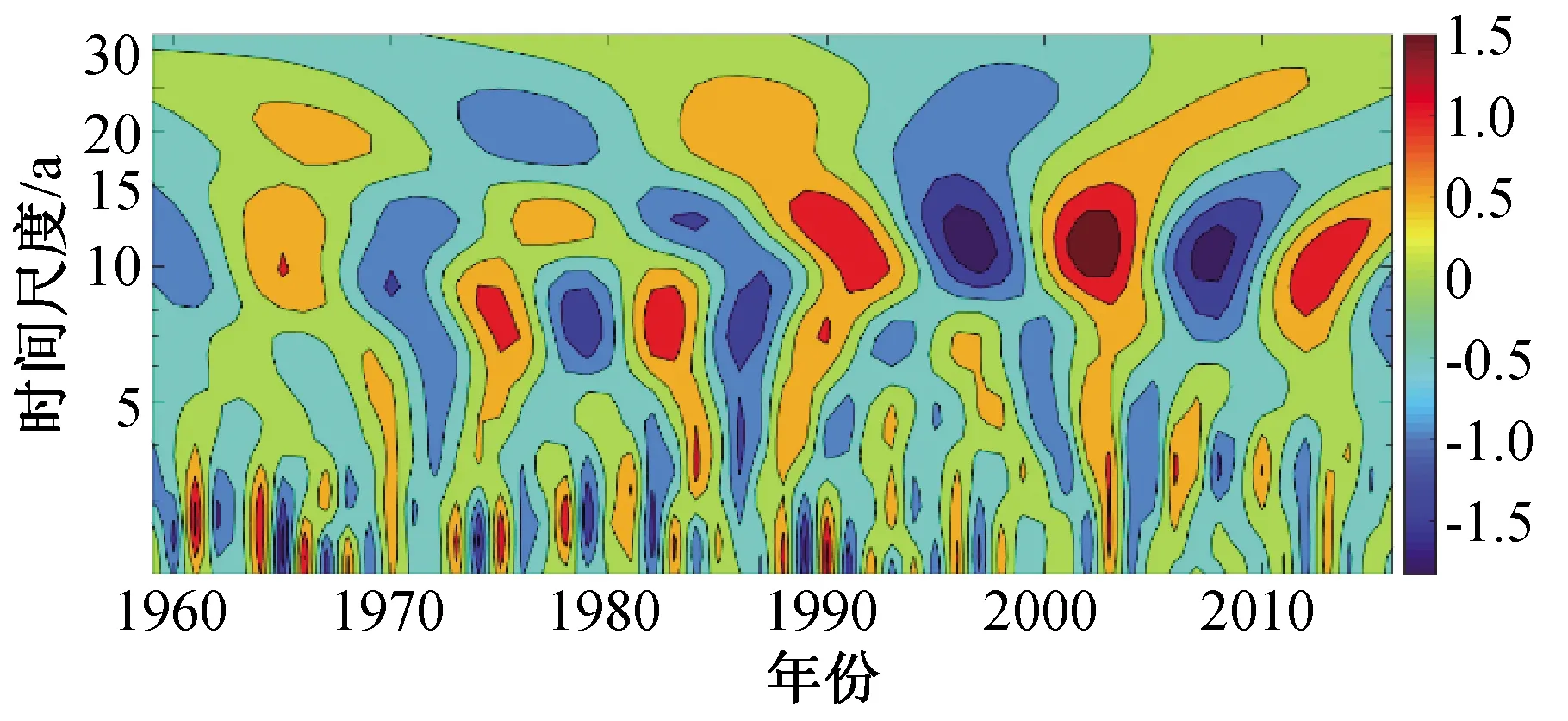
图8 西峰站点年降水时序小波系数实部时频分布图Fig.8 Real part time-frequency distribution of wavelet coefficients of annual precipitation at Xifeng station

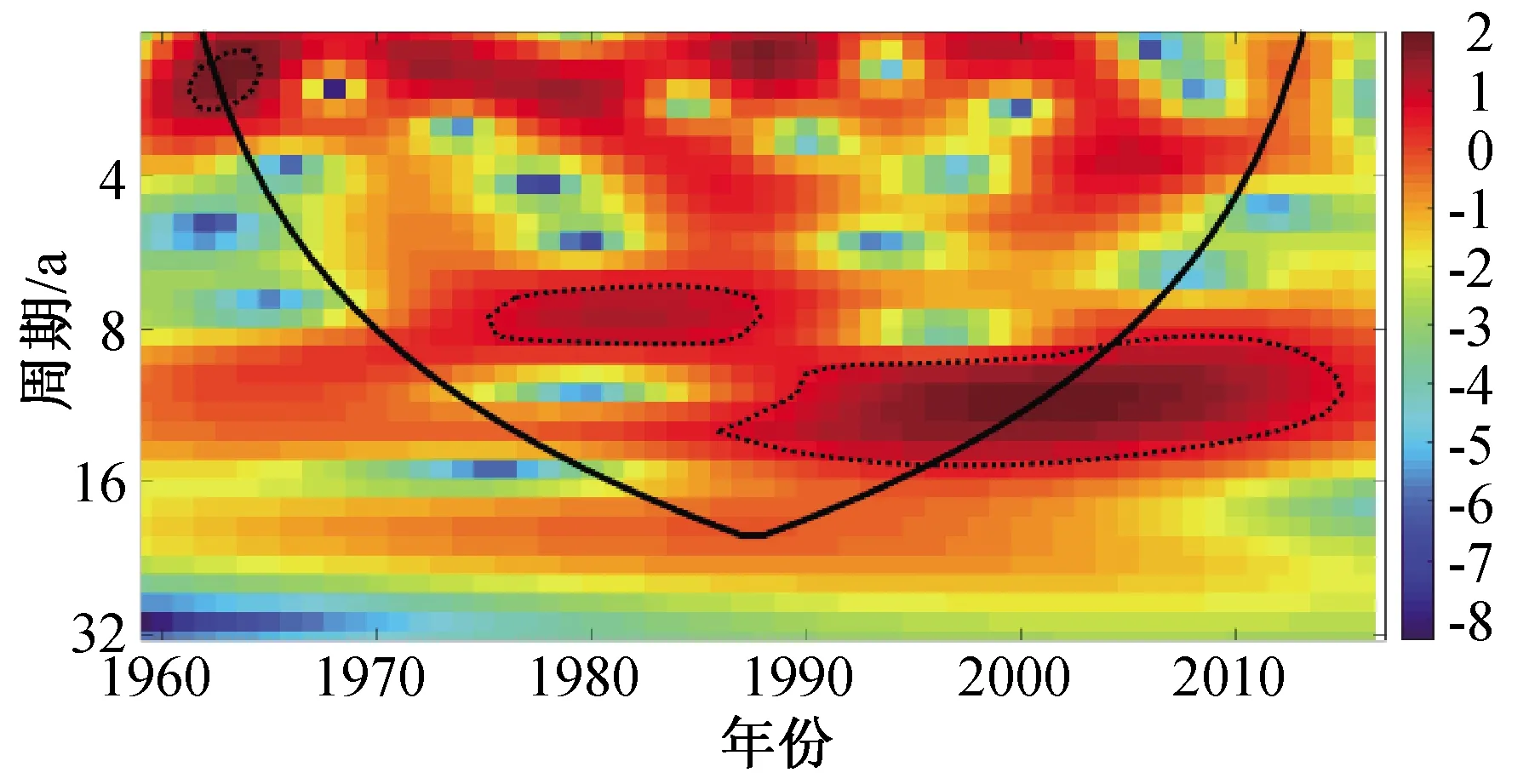
图9 西峰站点年降水时序小波功率谱Fig.9 Wavelet power spectrum of annual precipitation time-series at Xifeng station

3.3.2 长武年降水量的小波分析结果

对于长武地区，根据图10、图11可见其存在三种时间尺度变化周期，分别为1～2年、4～5年、7～9年时间尺度。时间尺度7～9年在能量上占了主要部分，是影响未来该地区降水量的主要时间尺度，该时间尺度在20世纪70年代初到80年代末趋势显著，震荡中心显示其枯水与丰水期的交替周期约为8年。1～2年左右的周期，主要存在于20世纪60年代初和70年代末。而4～5年左右的周期主要存在于20世纪80年代末和21世纪00年代末。

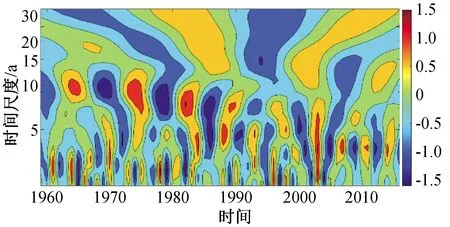
图10 长武站点年降水时序小波系数实部时频分布图Fig.10 Real part time-frequency distribution of wavelet coefficients of annual precipitation at Changwu station

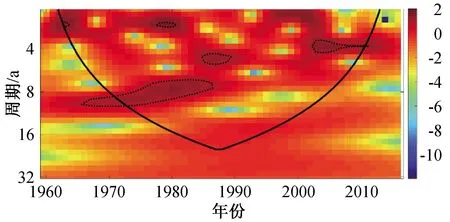
图11 长武站点年降水时序小波功率谱Fig.11 Wavelet power spectrum of annual precipitation time-series at Changwu station

综合分析得到，董志塬地区年降水量受2年、4年和8年的尺度波动所影响，时间尺度8年在能量上占了主要部分，是影响未来该地区降水量的主要时间尺度，主要出现在20世纪70年代到80年代末；董志塬地区年降水量时间序列的主周期为8年，以8年为周期振荡，震荡中心在1980年。董志塬地区降水的丰枯交替明显，董志塬地区整个时间序列上的年降水量呈现出上升下降的循环交替特征。