电动平台车调平系统优化研究

唐火红，王 鑫，栾 铸

（合肥工业大学机械工程学院，安徽 合肥 230009）

1 引言

电动平台车广泛应用于建筑、消防、检修等领域，其调平系统直接影响整机的工作性能[1-2]。目前常见的调平系统包括自重调平系统、平行四连杆调平系统、静液压调平系统以及电液调平系统[3-4]。

这里研究的电动平台车作为飞机机翼无损检测设备的搭载平台，对调平系统的调平精度有较高要求。它采用静液压调平系统，该系统结构简单、成本低并且不易受外在系统干扰，在一次调平过程中，油液温度和压力的变化对调平精度影响小[5-6]。文章首先分析影响静液压调平系统调平精度的主要因素，然后运用ADAMS软件建立静液压调平系统的参数化模型，以调平误差的最小作为优化目标，对该调平系统进行优化设计，得到新的铰点位置参数。根据该位置参数设计样机的调平系统，并对样机调平误差进行试验测试。测试结果表明，样机具备较高的调平精度，该优化方法能够为静液压调平系统的设计提供指导。

2 静液压调平系统调平机理分析

研究的电动平台车静液压调平系统，主要由臂架、平衡油缸、调平油缸和吊篮平台构成，如图1所示。静液压调平系统采用油液体积不变原理，由两个结构尺寸完全相同的平衡油缸和调平油缸组成一个封闭的自动调平回路，平衡油缸伸出（缩回）的长度等于调平油缸缩回（伸出）的长度，通过两个油缸的联动实现调平[7-8]。与立柱总成相连的平衡油缸为主动油缸，其与立柱总成铰接点为B点，与臂架铰接点为C点，臂架与立柱总成的铰接点为A点，A、B、C三点组成一个三角形，其中AB与AC两条边长度固定，在臂架变幅过程中，平衡油缸伸出或缩回，BC长度变长或缩短。与吊篮平台相连的调平油缸为被动油缸，其与吊篮平台铰接点为F点，与臂架铰接点为E点，臂架与吊篮平台的铰接点为D点，D、E、F三点组成另外一个三角形，DE和DF两条边长度固定，随着臂架的变幅，调平油缸缩回或伸出，改变吊篮平台与地面的夹角，从而保证水平。

图1 电动平台车静液压调平系统示意图Fig.1 The Static Hydraulic Leveling System of Electric Platform

根据图1中的臂架变幅过程，分析该系统的调平机理。臂架向上变幅时，平衡油缸伸出，油缸与臂架的铰接点C绕着B点逆时针旋转到C′点，臂架仰起的角度为∠CAC′，此时，平衡油缸有杆腔中的油液被压出，经过管路，流入调平油缸的有杆腔，调平油缸收缩，油缸与吊篮平台的铰接点F绕着E点顺时针旋转到F′点，吊篮平台下落的角度为∠FDF′。将∠CAC′称为臂架变幅角，∠FDF′称为吊篮平台调平角，如图2所示。

图2 变幅角与调平角Fig.2 Luffing Angle and Leveling Angle

当变幅角与调平角相等，即∠CAC′=∠FDF′时，吊篮平台水平，∠CAC′为∠BAC′与∠BAC的差值，令∠BAC′=θ1（t），则∠BAC=θ1（0），∠CAC′＝Δθ1（t）＝θ1（t）-θ1（0），∠FDF′为∠ΕDF与∠ΕDF′的差值，令∠ΕDF′=θ2（t），则∠ΕDF=θ2（0），∠FDF′=Δθ2（t）=θ2（0）-θ2（t）。设平衡油缸伸缩速度为v，其由臂架变幅速度决定，根据设计要求，选取v=5mm/s，另外，BC为平衡油缸收缩时的长度，EF为臂架最大变幅时，调平油缸伸出时的长度。则有如下表达式：

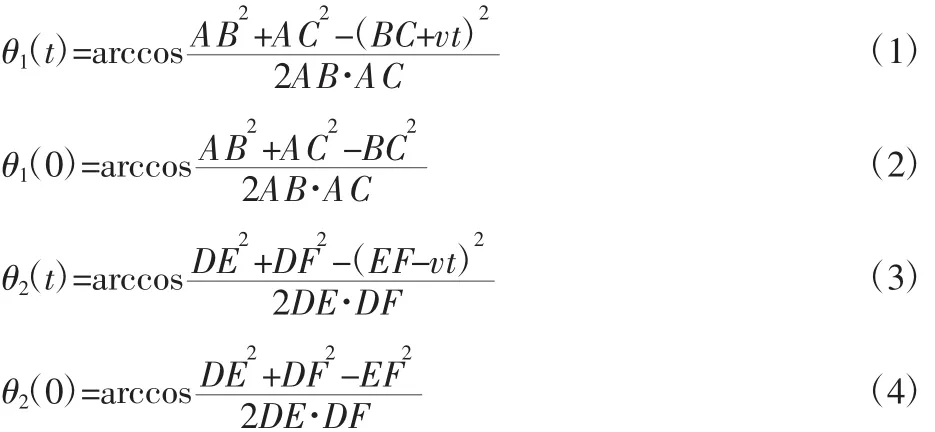
通过以上对调平机理的分析，吊篮平台的调平误差即为变幅角与调平角的差值，该差值用 Δθ（t）表示，Δθ（t）越小即表明调平精度越高，当 Δθ（t）＝0 时，该吊篮平台水平。Δθ（t）的数学表达式如下：

由该表达式可知，调平误差Δθ（t）的大小会随着臂架的变幅发生变化。在油缸伸缩速度一定的情况下，其大小与AB、AC、DE、DF长度有关，即与调平系统中各铰接点的位置布置有关。

3 基于ADAMS的参数化建模及仿真优化

运用ADAMS的参数化设计与优化分析功能[9]建立静液压调平系统参数化模型，对各铰接点位置进行优化设计，通过合理布置各铰接点位置实现调平误差的最小。

3.1 参数化建模

为减少设计变量，选取AB=DE，令A点与D点重合，B点与E点重合，并将A点作为坐标原点，则A、B、C三点代表与平衡油缸有关的三个铰接点，A、B、F三点代表与调平油缸有关的三个铰接点。定义B点坐标为（DV_1，-DV_1），C点坐标为（DV_2x，DV_2y），F点坐标为（DV_3x，DV_3y）。根据油缸选型及设计要求可知BC为平衡油缸伸缩时的最小长度，BF为调平油缸伸缩时的最大长度，则BC=450mm，BF=600mm，C点横坐标DV_2x可表示为DV_2y、DV_1的函数，其表达式为：

D点横坐标DV_3x可表示为DV_3y、DV_1的函数，其表达为：

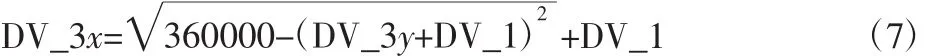
使用目前静液压调平系统设计中常用的试凑方法，确定各铰接点的位置参数，如表1所示。

表1 优化前各铰接点位置参数Tab.1 Position of Each Hinge Point Before Optimization

图3 调平系统参数化模型Fig.3 Parameterized Model of Leveling System

根据表1中参数，建立静液压调平系统参数化模型，如图3所示。在该调平系统参数化模型中，构件BC代表平衡油缸，其由缸体和活塞杆构成。将缸体和活塞杆之间的移动副约束添加在B点上，移动副方向设置为ORI_ALONG_AXIS（POINT_B，POINT_C，‘Z’）。构件BF代表调平油缸，其缸体与活塞杆之间的移动副建立过程与构件BC中建立过程相似。在移动副约束添加完成后，给两个移动副添加驱动，根据油缸实际伸缩速度，平衡油缸的驱动函数设置为v=5mm/s，调平油缸的驱动函数设置为v=-5mm/s，保证平衡油缸伸出长度等于调平油缸收缩长度，模拟实际油缸伸缩及系统调平过程。

3.2 定义约束

根据电动平台车的结构和空间限制要求，确定设计变量的变化范围为：

160mm≤DV_1≤220mm

-200mm≤DV_2y≤-150mm

220mm≤DV_3y≤260mm

由电动平台车的变幅动作要求可知，C点需要位于AB构件右侧，故满足：

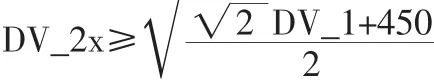
3.3 调平系统仿真

在完成静液压调平系统参数化建模后，根据式（5）创建输出函数Δθ（t），其中，θ1（t）、θ1（0）、θ2（t）、θ2（0）为ADAMS中建立的四个测量函数。对采用试凑方法设计的静液压调平系统进行仿真，得到其调平误差Δθ（t）的变化幅度较大，调平误差最大值为1.41°。

3.4 调平系统优化设计

优化分析是ADAMS提供的一种高级参数化计算、分析工具，在设定的变化范围内，通过分析程序自动地调整设计变量，求取系统铰接点的最佳布置位置[10]。

基于ADAMS的优化设计必须给定设计的目标函数、约束条件以及设计变量。由于之前已建立了参数化模型并定义了约束，因而，仅需将输出函数 Δθ（t）定义为模型的目标函数，并以 Δθ（t）最小作为模型的优化目标，即可对调平系统进行优化设计。

为了加速优化过程，减少仿真过程中的迭代次数，首先利用ADAMS中的实验设计功能，对各个设计变量逐一进行优化分析，找出设计变量中比较好的初始值，然后再进行优化计算。调平误差Δθ（t）在每次迭代过程中随时间变化的曲线，如图4所示。由图中可知，经过优化，调平误差Δθ（t）的最大值达到最小为0.36°，比优化前减少了1.05°，另外，在臂架变幅过程中调平误差变化幅度减小。该调平系统经过优化后的各铰接点位置参数，如表2所示。选取经过优化设计得到的各铰接点位置参数，对调平系统进行仿真，将调平误差随时间的变化曲线与臂架变幅角度随时间的变化曲线导出，从而得到调平误差与臂架变幅角度的关系，以方便后期同样机的调平误差测试结果对比，论证该仿真模型建立的正确性及优化设计方法的合理性。

表2 优化后各铰接点位置参数Tab.2 Position of Each Hinge Point After Optimization

图4 优化过程中调平误差随时间变化曲线Fig.4 The Curve of Leveling Error with Time in the Process of Optimization

4 样机试验与对比分析

根据ADAMS优化得到的各铰点位置参数，设计电动平台车调平系统，并对样机进行试验，测量吊篮平台的调平误差，将试验结果与仿真优化结果对比。

以电动平台车样机作为试验对象，测量吊篮平台的调平误差，测量系统包括传感系统和数据采集及分析系统。将角度传感器安装于臂架上，用以测量当前臂架角度，将倾角传感器安装于吊篮平台上，用来测量吊篮平台的倾角，所测平台的倾角即为调平误差。由于测量过程中臂架变幅运动是连续的，因此试验采用随机取点的方法来获得每个采样点的臂架角度及吊篮平台倾角，该电动平台车样机的试验测试过程，如图5所示。在本次试验中，臂架按（0～50）°变幅，50°为样机的最大变幅角。试验最终测得20组数据，利用MATLAB绘制试验数据的拟合曲线，并将仿真得到的调平误差随臂架变幅角度的变化关系与该拟合曲线对比，对比图，如图6所示。两条曲线具有相似的变化趋势，并且仿真结果与试验结果之间误差较小，最大误差为0.03°，最大误差百分比为17.1%。初步推测导致该误差的主要原因有：（1）平衡油缸的伸出速度与调平油缸的收缩速度不完全一致，调平过程存在滞后。（2）零件的生产加工和装配存在误差。

图5 电动平台车样机试验测试过程Fig.5 Testing Process of Electric Platform

图6 试验结果与仿真结果对比曲线Fig.6 Contrast Curve Between Test Results and Simulation Results

5 结论

以电动平台车静液压调平系统作为研究对象，经过理论分析，推导出影响其调平精度的主要因素为调平系统中各铰接点的位置。运用ADAMS建立调平系统的参数化模型，以调平误差Δθ（t）的最小作为优化目标，对各铰接点位置进行优化设计，经过优化，调平误差曲线得到显著改善，调平精度提高。

根据仿真优化得到的各铰点位置，设计电动平台车样机的调平系统，并对样机调平误差进行试验测试。测试结果表明，该调平系统具备较高的调平精度，样机的实际调平误差与优化后仿真得到的系统调平误差之间相差较小，验证了基于ADAMS的静液压调平系统参数化建模的正确性及优化设计方法的合理性，该优化方法便于理解，设计变量易于修改，并且优化结果较直观，可为静液压调平系统的设计开发提供数据支撑，也可用于类似铰点问题的优化。