基于Matlab的一种调平装置调平机构运动分析

卢月红, 卢发中

(厦门华厦学院 信息与机电工程系，福建 厦门 361024)

在现代化工业中，时常需要把某些设备的工作平面调整到水平位置，从而保证设备系统的运行精度、测量精度等其它工作性能指标.调平装置是把试验设备工作平面的水平调整到适合使用要求的一种装置，是保证许多设备正常工作的前提条件，调平装置在现代化工业中发挥着越来越重要的角色[1].调平机构是调平装置的关键部件，调平机构的调平性能在很大程度上决定了调平装置的使用性能.因此，调平机构的研究具有重要的现实意义.

机构运动分析是机械设计的基础，通过机构运动分析可以得到关注构件或构件上特定点的轨迹、位移、速度以及加速度[2-3].机构分析的方法有图解法和解析法.图解法需反复作图，工作量大而且精度低.随着科技的进步，计算机技术得到了飞速发展，解析法得到了广泛应用[4].利用计算机进行仿真求解，在得到高精度的同时还可以将计算结果图形化，更易于深入分析与研究.本文利用Matlab所具有的数值计算和图解功能对调平机构进行运动分析，为设计出满足工作要求的调平装置提供可靠的数学依据.

1 调平机构调平原理

图1 调平机构简图

本文研究的调平机构主要由被调平筒状部件和移动组件组成，其中移动组件由连杆、连杆座、滚珠丝杠导轨、步进电机和联轴器构成.被调平平面为筒状部件底部平面，由于需要实现X和Y两个方向调平，故选用两套步进电机、滚珠丝杠导轨和连杆组合分别对X、Y两个方向进行调平，采用绕轴旋转的方式——被调平平面绕Y轴旋转，实现X方向调平；被调平平面绕X轴旋转，实现Y方向调平.初步设计外筒、中筒分别用于支撑中筒、内筒.外筒和中筒，中筒和内筒之间分别在径向采用轴连接，内筒、中筒分别绕自己的轴旋转，实现被调平平面X、Y向调平.调平机构简图如图1所示.

2 调平机构运动分析

通过对调平机构的运动分析，旨在得到调平机构滑块位移Sc与筒件转角θ的关系，绘制出在给定位移Sc的情况下，筒件高度h与筒件转角θ的关系图，从而进一步确定调平机构筒件的尺寸；通过得到的调平机构筒件尺寸，分析X轴向调平机构和Y轴向调平机构最大转角θmax，确定滑块最大位移Scmax.

2.1 建立机构运动分析的数学模型

如图2所示，AB为筒件，BC为连杆，C为滑块.根据建立的直角坐标系，不妨设AB的长度为m，方位角为θ1，BC的长度为n，方位角为θ2.

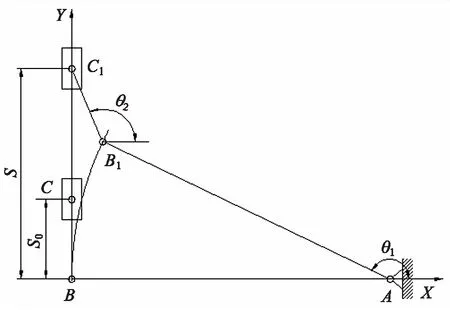
图2 调平机构运动分析简图

由图2所示的几何关系，可以得到以下矢量关系式：

AB1+B1C1=AB+BC1

(1)

可知：AB1的模为m，方位角为θ1；B1C1的模为n，方位角为θ2；BC1的模为S，方位角为90°；AB的模为m，方位角为180°.

将上述矢量方程写成复数矢量形式[5]：

meiθ1+neiθ2=-m+iS

(2)

将欧拉公式eiθ=cosθ+isinθ带入式(2)得：

m(cosθ1+isinθ1)+n(cosθ2+isinθ2)=-m+iS

(3)

化简后可得：

mcosθ1+ncosθ2=-m

(4)

msinθ1+nsinθ2=S

(5)

又转角θ=180°-θ1,S0=n.可得滑块位移:

(6)

2.2 数学模型求解

根据2.1建立的关系式(4)～(6)，利用Matlab软件进行程序设计，求解数学模型，部分程序代码如下[6-7]：

……

l1=m*cos(pi-theta)+n*cos(theta2)+m；

theta2=solve(l1,theta2)；%得到θ与θ2之间的关系……

l2=Sc-m*sin(pi-theta)-n*sin(theta3)+n；

m=solve(l2,m)；%得到筒件高度h与筒件转角θ之间的关系式

……

ezplot(m,theta)；%绘制筒件高度h与筒件转角θ的关系图

title(‘筒件高度h与筒件转角θ的关系图’,‘fontname’,‘黑体’,‘FontSize’,12)；

xlabel(‘筒件转角θ/rad’,‘fontname’,‘黑体’,‘FontSize’,12)；

ylabel(‘筒件高度h/mm’,‘fontname’,‘黑体’,‘FontSize’,12)；

grid on；

……

运行程序，可得到滑块位移Sc与筒件转角θ之间的数学关系：

(7)

同时绘制出给定滑块位移Sc=45 mm情况下，调平机构筒件高度h与筒件转角θ关系图，如图3所示.

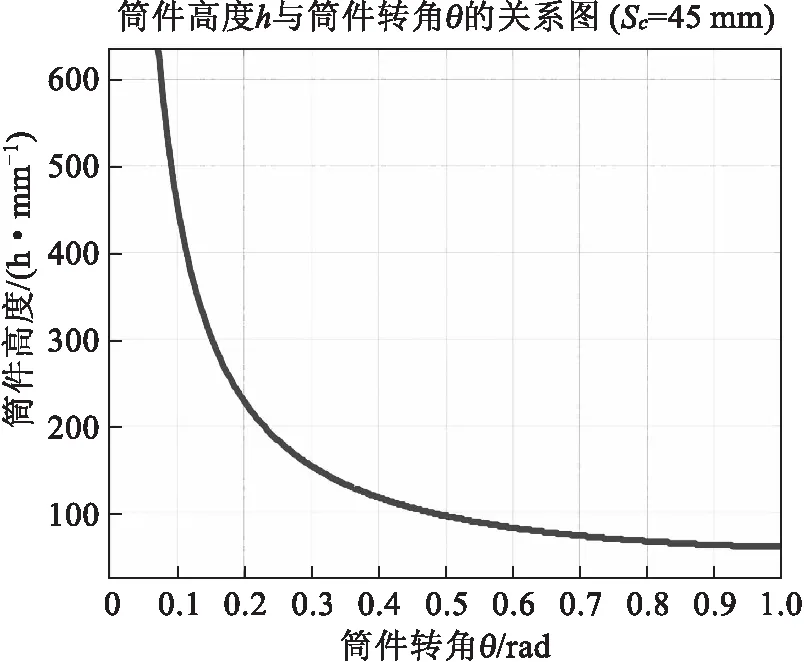
图3 调平机构筒件高度h与筒件偏转角θ关系图

由图3可知，在相同的滑块位移Sc下，调平机构筒件高度h越大，筒件转角θ越小.筒件转角越小说明调平机构调平精度和调平灵敏度越高.因此，可以根据实际情况，选择尽可能大的筒件高度，初步确定筒件的高度值为：中筒464 mm，内筒257 mm.

2.3 调平机构极限位置求解

调平机构在调平过程中，存在四个极限位置：X轴向调平机构最大转角θmaxX，Y轴向调平机构最大转角θmaxY以及滑块在X轴和Y轴上的最大位移ScmaxX、ScmaxY.

(1)X、Y轴向调平机构最大转角分析

从进口到出口，从供不应求到自给有余，在几代氮肥人艰苦奋斗和不懈努力下下，我国已经成为名副其实的世界氮肥大国，并在发展中不断调整产业结构、升级装置技术、淘汰落后产能，向氮肥强国稳步迈进。60年来，几代氮肥人自力更生、艰苦奋斗，开发了一系列技术、装备，有力地支撑了氮肥工业的发展。

如图4所示，调平机构在进行X轴向调平时，中筒会受到外筒的限制，中筒存在一个最大转角θmaxX；同理，调平机构在进行Y轴向调平时，内筒会受到中筒的限制，内筒存在一个最大转角θmaxY.由于滑块位移Sc与筒件转角θ之间存在确定的数学关系，因此通过对θmaxX、θmaxY进行求解，可以确定滑块的最大位移ScmaxX、ScmaxY，在导轨上设定限位开关，从而防止筒件间发生碰撞，保护调平机构，避免调平机构因碰撞发生形变或损坏而影响调平精度和灵敏度.[8]

由图4所示几何关系可得：

∠BAD=∠BCE=θ

(8)

CB=CE/cosθ

(9)

CB=CD+DB=CD+ADtanθ

(10)

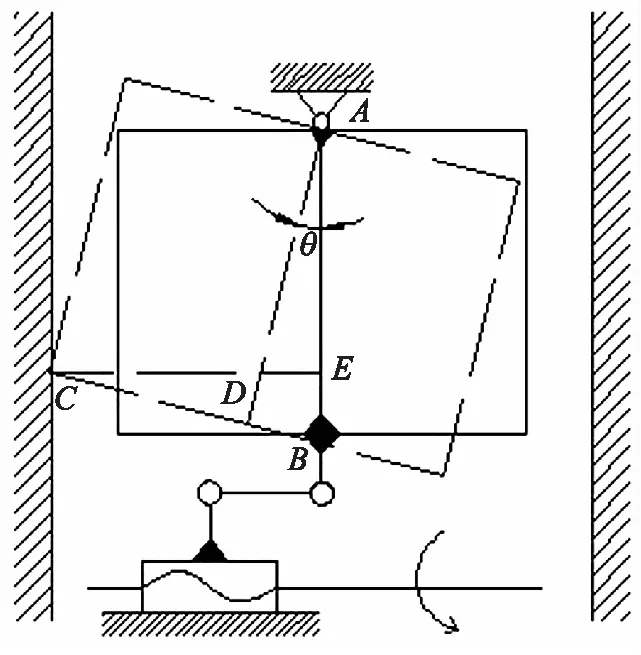
图4 X(Y)轴向调平机构最大转角分析图

对于X轴向调平机构，CD=182 mm，CE=210 mm，AD=464 mm；对于Y轴向调平机构，CD=158 mm，CE=182 mm，AD=257 mm.

根据上述分析，借助Matlab求解，部分求解程序如下：

%求X轴向最大转角

……

l1=input(‘中筒直径’)；

l2=input(‘外筒直径’)；

DE=input(‘中筒高’)；

l3=0.5*l1+DE*sin(theta)/(cos(theta))-l2/(2*cos(theta))；

theta=solve(l3,theta)；

theta=double(theta*180/pi)；

XMaxtheta=theta；

……

%求Y轴向最大转角

l1=input(‘内筒直径’)；

l2=input(‘中筒直径’)；

DE=input(‘内筒高’)；

l3=0.5*l1+DE*sin(theta)/(cos(theta))-l2/(2*cos(theta))；

theta=solve(l3,theta)；

theta=double(theta*180/pi)；

YMaxtheta=theta；

……

运行程序，求解得：

θmaxX=3.50°，θmaxY=5.52°

对于X轴向调平，m=467 mm，n=75 mm，θ=θmaxX=3.50°,带入式(7)得：ScmaxX=28.50 mm.

对于Y轴向调平，m=257 mm，n=75 mm，θ=θmaxY=5.52°,带入式(7)得：ScmaxY=24.71 mm.

因此，为避免滑块发生碰撞，应在导轨相应位置设定限位开关，避免X轴、Y轴滑块位移超过最大位移.

3 结语

本文详细说明了调平机构调平原理，运用矢量法和解析法建立调平机构运动数学模型.使用Matlab软件进行程序设计求解数学模型，并绘制出调平机构筒件高度与筒件转角的关系曲线图，确定了筒件高度值，得到相关数值解，为调平机构的设计以及调平装置的研发提供了一定的帮助与理论支撑.[9]同时，本文也印证了Matlab在进行机构运动分析时所具有的强大数值计算能力和图解功能，为相似问题的分析研究提供一定的参考.