复杂产品设计变更传播多目标路径优化研究

李孟泽，盛健超，李玉鹏，亓文辉

（中国矿业大学矿业工程学院工业工程系，江苏 徐州 221116）

1 引言

复杂产品的设计变更对于企业快速适应市场变化，响应多样化的客户需求起着举足轻重的作用[1]。企业为了保持核心竞争力，经常要对产品进行设计变更。变更的传播可能会影响产品研发进度和产品质量。另外，复杂产品的零部件之间结构关系错综复杂，变更的传播会使开发过程的难度提高，增加设计成本和风险。

针对设计变更问题，国内外学者开展了深入的研究。如文献[2]提出了公理化设计矩阵与设计结构矩阵（Design Structure Matrix，DSM）同步演化的思想，并阐述了其演化的内在机制。文献[3]运用网络层次分析法评估模块化产品设计变更传播的影响，该方法仅仅适用于解决模块化产品问题，而对于难以实现模块化的产品其优势并不明显。文献[4]对产品设计变更进行了并行处理，以变更处理时间作为判据来搜索最优的传播路径。文献[5]以累积变更传播强度最小为目标，根据零部件参数连接关系建立设计变更分析模型，运用改进的蚁群算法进行求解。总之，虽然有关设计变更传播的研究较为丰富，但针对复杂产品设计变更多目标路径优化问题，没有进行针对性的研究。

近年来，复杂网络理论的兴起为解决复杂产品设计变更问题提供了新思路，复杂产品的零部件可以抽象为网络的节点，物理或功能关联关系可以抽象为网络中的边。目前，常见的复杂网络有随机网络（ER模型）[6]、无标度网络（BA模型）[7]以及小世界网络（WS模型）[8]。文献[9]将有向加权网络看作复杂产品的形式化表达，对设计变更的影响进行分析。文献[10]基于BBV无标度网络演化模型，对复杂产品设计变更传播影响进行定量化评估。

鉴于以上研究，首先根据复杂产品零部件的物理连接关系构建复杂网络，根据变更传播特点建立设计变更多目标路径优化模型，运用蚁群算法求解得到最优传播路径，所得最优方案可有效节省设计时间和成本，降低变更影响。

2 复杂产品设计变更网络模型构建

2.1 小世界网络模型

Watts等在1998年提出了一种介于规则网络和随机网络之间的小世界网络模型，该理论的提出是复杂网络研究的一项开创性成果。小世界网络有两个重要的特征参数：特征路径长度L和聚类系数C。

（1）特征路径长度是任意两个节点之间最短距离的平均值，表示为：

式中：dij—任意两个连通节点间的最短距离。

（2）聚类系数用于衡量相邻节点联系紧密程度，表示为：

式中：di—节点vi的度；ti—节点vi的相邻节点之间存在的边数。小世界网络具有很高的聚类系数和较小的平均距离。可以

表示为：

式中：Cr、Lr—对应随机网络的聚类系数和平均距离。

2.2 变更传播模型构建

为了建立变更传播模型，首先将复杂产品分解为有着物理连接关系的零部件。将零部件之间的关系映射为n×n阶方阵，即产品的DSM。若零件ai的变更会引起零件aj的变更，则aij=1（i≠j），反之aij=0。一个包含6个零部件的产品，容易发现，若零部件a1发生设计变更，则零部件a2和a6有可能会受到影响，如图1所示。

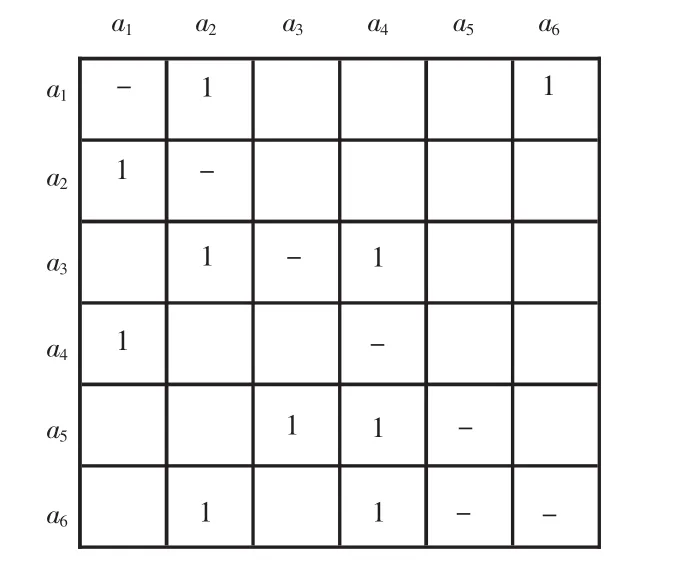
图1 设计结构矩阵Fig.1 Design Structure Matrix

依据产品的DSM构建变更传播模型，其网络模型可以表示为 G=（V，E），V=（v1，v2，…，vn）为节点的集合，E=｛eij|i，j=1，2，…，n，i≠j｝为边的集合。节点代表DSM中的元素，节点间的连接边代表元素之间的关系，从而确定节点之间是否存在连接关系。

2.3 变更传播强度评估

从工程变更角度看，复杂产品可以由大量节点与边构成的复杂网络表示，网络中的节点代表产品的零部件，边代表零部件之间的物理连接关系。在对产品的复杂网络拓扑结构的统计特征进行分析后发现，其特征路径长度和聚类系数满足式（3），具有小世界特性[11]。在该网络中，网络节点的度对设计变更的传播起着重要作用[12]，某个节点度越大，它对应的传播路径越多，扩散范围就越大。

定义变更传播强度与传播概率和节点的度有关。传播概率Pij表示节点vi传播到节点vj的可能性大小。当节点vi和节点vj之间没有连接边，则Pij=0；当节点之间传播概率越大，变更传播越倾向经过该连接边。dj表示节点vj的度。度大的节点拥有较多连接边，变更传播的影响范围比较大。用Fk表示传播第k步可达到节点集合。变更传播强度定义为：

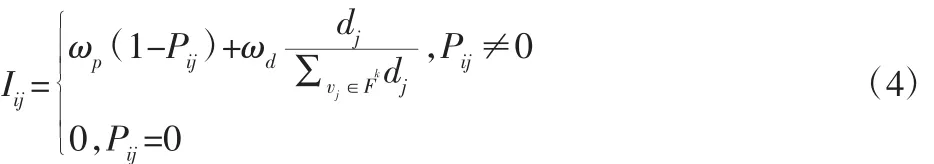
式中：ωp+ωd=1，ωp和ωd—传播概率和节点度对应的权重。在与相关专家确定后ωp=ωd=0.5较为合适。在上述分析中，变更传播强度的大小代表复杂网络中节点之间的边权，权重越大，表示变更通过此边进行传播产生越大的影响。

3 设计变更传播路径搜索算法

3.1 设计变更传播方式

零部件的变更传播存在两种方式：串行传播和并行传播。对于串行传播，如图2（a）所示。零件变更的传播是依次进行的；对于并行传播，如图2（b）所示。一个零件的变更可以同时影响多个零件，其传播路径是由多个串行传播路径组成。在实际传播中，两种变更传播方式都存在。

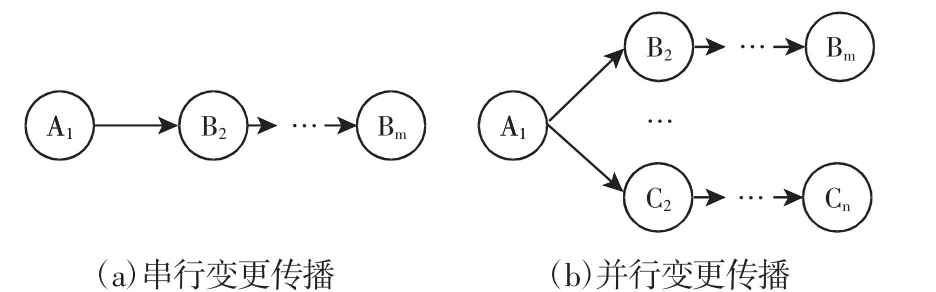
图2 变更传播方式Fig.2 Change Propagation Patterns

3.2 设计变更传播最优路径搜索

设计变更传播路径的搜索是一个NP-hard问题[13]，运用启发式算法求解此类问题有较好的效果。蚁群算法是文献[14]提出的一种启发式智能优化算法，已成功应用于求解许多NP问题、组合优化问题等，如旅行商问题、车辆调度问题。因此，采用蚁群算法求解复杂产品的设计变更传播路径优化问题。基于已建立的复杂网络模型，以变更传播强度、零件设计成本和设计时间为多个优化目标，将复杂产品设计变更多目标路径优化的数学模型描述为：

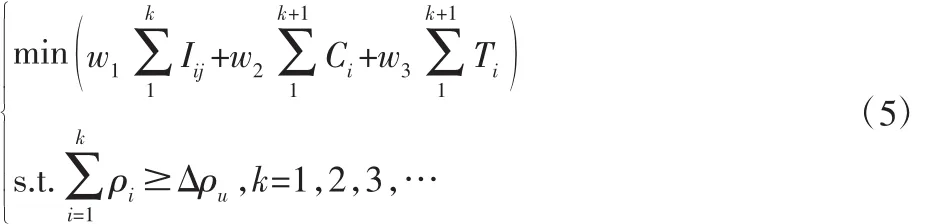
式中：Ci—零件ai的设计成本；Ti—零件ai的设计时间，目标函数为传播路径上的变更传播强度、零件的设计成本和设计时间的加权总和最小。Δρu—初始变更节点的初始变更影响。为了让变更传播停止，定义ρi为节点vi的变更吸收能力，k为变更传播的步数。

在寻找最优路径的过程中，蚂蚁会在其经过的路径上留下信息素，之后的蚂蚁会根据这些信息素的强弱选择路径。每一次循环迭代，蚂蚁的信息素更新按如下规则：

式中：Q—常数；Dl—第l只蚂蚁在本次循环的目标函数值；γ—信息挥发系数；Δτlij—在本次循环中第l只蚂蚁留在边eij上的信息素；Δτij—在本次循环中边eij上的信息素的增量。因为变更优先选择传播影响小的边进行传播，所以定义启发因子为：

式中：传播影响Aij=ω1Iii+ω2Ci+ω3Ti，该启发因子表示蚂蚁从节点vi到节点vj的期望程度。第l只蚂蚁从节点vi到节点vj的转移概率为：

式中：α（α≥0）—信息素的相对重要程度，即轨迹的相对重要性；β（β≥0）—启发因子的相对重要程度，即能见度的相对重要性；—第l只蚂蚁在节点vi下一步允许选择的节点集合。运用蚁群算法寻找变更传播最优路径的搜索步骤，如图3所示。

图3 最优变更传播路径搜索算法框架Fig.3 Algorithm Framework of Optimal Change Propagation Path Searching

（1）通过对复杂产品各零部件之间连接关系分析，将零部件映射为节点，物理连接关系映射为边，建立复杂产品网络模型。

（2）依据复杂网络模型，计算每个节点的出入度；通过从数据库中提取节点与节点之间传播概率。利用式（4），计算每条边的变更传播强度。

（3）输入初始变更节点。评估每个节点变更吸收能力，设置初始变更节点影响，运用蚁群算法进行求解，得到最优的传播路径。

4 案例分析

为了验证所建模型和算法的有效性，以某型号摩托车发动机为例进行分析。产品由汽缸盖，气门，气门固定螺母，曲柄销，气缸垫片，气门固定轴，曲轴箱，活塞等30种零部件组成。根据该发动机零部件间的物理连接关系，得到产品的DSM，并建立零部件结构网络模型，如图4所示。

图4 零部件结构网络模型Fig.4 Structure Network Model of Parts

在设计变更传播的路径搜寻过程中，根据设计变更历史数据库得到经过每条边的概率，如图5所示。图中为30阶方阵，每一方格的颜色深浅代表传播概率的大小，颜色越深表示概率越大，变更传播越容易经过这条路径。依据式（4）计算得到每条边的变更传播强度以及由产品设计变更数据库得到的每个零部件的设计成本和设计时间，经过计算得到的发动机变更传播影响矩阵，如图6所示。气缸体是摩托车发动机的重要零部件，且在现实生活中容易发生变更，故选取节点编号为22的气缸体为初始变更节点，初始变更影响设置为0.30，运用蚁群算法求解。算法通过VisualStudio2013进行开发，运行算法的计算机配置为IntelR CoreTMi5-3210M CPU（2.5 GHz），4GB RAM，得到最路径为 22→30→21→19→4→25。为说明所提方法的有效性，仅考虑变更传播强度单个目标所得最优路径为22→1→30→19→10→21。由以上结果比较得出，如果仅考虑变更传播强度，单目标设计变更传播最优路径的变更传播强度（2.52）小于多目标求解时变更传播强度（2.80）。但在比较其设计成本和设计时间时，发现后者的设计总成本和总时间分别为2220元和23天，都远高于前者的设计总成本和总时间：1970元，18天。如果在变更传播强度没有很大差距的情况下，对前者路径上的零件进行变更，将会节省大量的设计时间和设计成本，提高设计的敏捷性。

图5 传播概率矩阵Fig.5 Matrix of Propagation Likelihood

图6 发动机变更传播影响矩阵Fig.6 Matrix of Change Propagation Impact on Engine

5 结论

针对复杂产品设计变更传播多目标优化问题，提出了一种基于小世界网络的方法。该方法考虑了节点的度和节点间的传播概率两个变量计算变更传播强度，又引入零件的设计成本和设计时间，建立设计变更传播多目标路径优化模型，运用蚁群算法求解得到一条传播影响最小的路径。在实例研究中，以某型号摩托车发动机为例，对上述模型和算法进行了验证。所提方法仅从零件层次考虑，对设计变更传播的影响进行了分析，得出有效的结论。由于变更的执行必须要从零部件的设计参数着手，未来我们将会从复杂产品零部件的参数角度考虑展开研究。