涡轮转子无螺栓挡板过渡态热固耦合响应分析
2020-06-20孙海鹤秦仕勇庞燕龙
孙海鹤,秦仕勇,庞燕龙,任 芳,何 云,卿 华
(中国航发四川燃气涡轮研究院,成都 610500)
1 引言
航空发动机涡轮转子在各种工作状态转换过程中承受着剧烈变化的瞬态热载荷与机械载荷,会对涡轮转子造成显著的疲劳损伤[1-2]。现有统计表明,我国在现役航空发动机工程应用与在研型号研制中暴露出的若干问题均与加减速过渡态相关[2]。涡轮转子无螺栓挡板结构由于取消了轮盘与挡板连接的螺栓和螺孔,有效避免了螺孔的应力集中,成为先进涡扇发动机涡轮转子普遍采用的结构形式[3-5]。无螺栓挡板通常设计成质心半径较大的薄壁结构,往往无法承受自身高转速引起的离心载荷,需要涡轮盘轮缘径向定位面支撑作用才能保证其具有足够的强度储备。因此,航空发动机工作状态下的无螺栓挡板与涡轮盘配合稳定可靠至关重要。
目前国内针对无螺栓挡板结构设计和研究,主要集中于稳态载荷下轮盘或叶片与挡板配合面挤压力关系,未涉及发动机加减速过程瞬态热效应与离心载荷共同作用下的涡轮转子的过渡态响应。如栾永先等[6]通过有限元计算得出了气体压差、离心力载荷作用下无螺栓挡板与叶片轴向配合面挤压力规律。孟庆迪等[7]分析了离心力作用下高压涡轮后挡板不同区域内最大等效应力与转速的关系。王庆平等[8]讨论了双配合面无螺栓挡板结构稳态温度场和离心力作用下径向定位面应力与变形的协调关系,提出了双配合面无螺栓挡板结构设计的一般原则。尽管一些学者认识到涡轮转子以及无螺栓挡板在过渡态情况下的相关设计问题,如马健等[5]指出设计中需要考虑过渡态及急停过程中挡板径向配合面可能出现松弛甚至间隙从而破坏定心关系的问题,但是仍然缺乏对其原理和规律的阐释。国外在这方面的研究也鲜有报道。
本文针对涡轮转子无螺栓挡板结构开展过渡态温度与应力响应历程分析,研究发动机过渡态下无螺栓挡板受力与变形规律,可为涡轮转子无螺栓挡板设计提供参考。
2 涡轮转子结构
某型发动机高压涡轮转子采用“高压锅盖”式无螺栓连接挡板结构(图1),其主要特点是涡轮盘与挡板内缘配合安装边有对应的凹凸结构。装配时,挡板上的凹槽对准涡轮盘上的凸耳轴向压装到位,然后周向旋转特定角度,使挡板内缘的凹槽与轮盘对应的凸耳对齐,此时涡轮盘和挡板的轴向接触面处于过盈状态,弹性恢复力使两个零件紧密连成一体,从而达到轴向定位和紧固的目的。最后用限位销或限位块实现周向定位[9]。
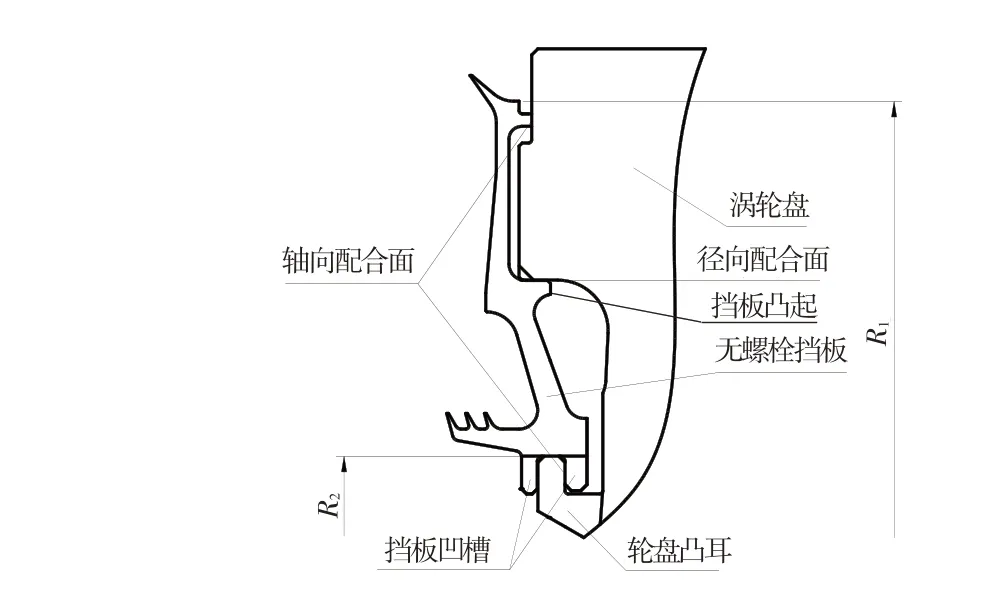
图1 涡轮转子装配示关系示意图Fig.1 Schematic illustration of turbine rotor assembly
3 分析方法及流程
3.1 过渡态响应分析方法
采用有限元方法对涡轮盘、无螺栓挡板构成的涡轮转子进行过渡态分析,以获取无螺栓挡板加减速试车历程过渡态温度场和应力变形历程。采用二维模型进行试车历程计算,以分析加减速试车过程中涡轮转子温度场特点和零件间的相互作用关系。为研究无螺栓挡板与涡轮盘配合面状态变化规律,分别在热分析和应力分析中以接触单元形式考虑配合状态变化对传热和传力的影响。
3.1.1 热分析模型
在热分析工程应用中,通常使用接触热导率h对接触面的热量传递情况进行计算和分析。

式中:Q 是通过接触面的全部热量,A 是表观接触面积,ΔT 是接触面两侧温差。实际问题中,通过接触面的热量可分为经接触点传递的热量Qs和经接触面填充介质传递的热量Qg两部分,则:

式中:hs、hg分别为经接触点传递和经接触面填充介质传递热量的热导率。
根据轮盘与挡板结构的几何特征,获得发动机机械零件接触热导率经验关系式[10-12],对涡轮转子不同换热类型划分区域,选用对应的换热特性准则关系式应用内部程序进行换热边界条件计算,在ANSYS软件中完成模型前处理与瞬态温度场计算。
3.1.2 应力分析模型
涡轮盘及无螺栓挡板周向连续部分采用ANSYS 轴对称模型建模(图2),挡板凸起、轮盘凹槽、轮盘榫槽和涡轮叶片等周向不连续部分采用平面应力单元建模,以模拟其子午面内刚度和质量离心力;无螺栓挡板与涡轮盘的配合面建立接触单元。工作转速、气体压力以试车历程的时间为参量,通过ANSYS表格加载方式协调加载。温度场载荷根据热分析结果按时间映射到应力分析网格。

图2 涡轮转子有限元模型Fig.2 FEM model of the turbine rotor
3.2 过渡态响应分析流程
过渡态情况下,转速和温度场变化会引起无螺栓挡板与涡轮盘配合面挤压力变化,配合面挤压力变化又会引起配合面接触热阻改变进而导致温度场变化,形成传热与应力分析的耦合现象。采用有限元软件ANSYS 顺序迭代法处理传热与应力分析的耦合问题,分析流程见图3,主要步骤如下:①假设无螺栓挡板与轮盘配合面处接触热阻为零;②根据换热边界条件变化历程进行瞬态热分析,获得涡轮转子温度场变化历程;③将获得的温度场历程作为热载荷施加于结构模型,协调所有机械载荷进行瞬态应力分析,并输出挡板与轮盘各配合面挤压力变化历程;④检查计算收敛条件——参考点温度与上一轮温度差异是否小于ε,如不满足则根据挤压力历程数据更新传热模型中各配合面接触热导率后重复②、③步骤,直至满足收敛条件;⑤计算完毕输出传热和应力分析结果。
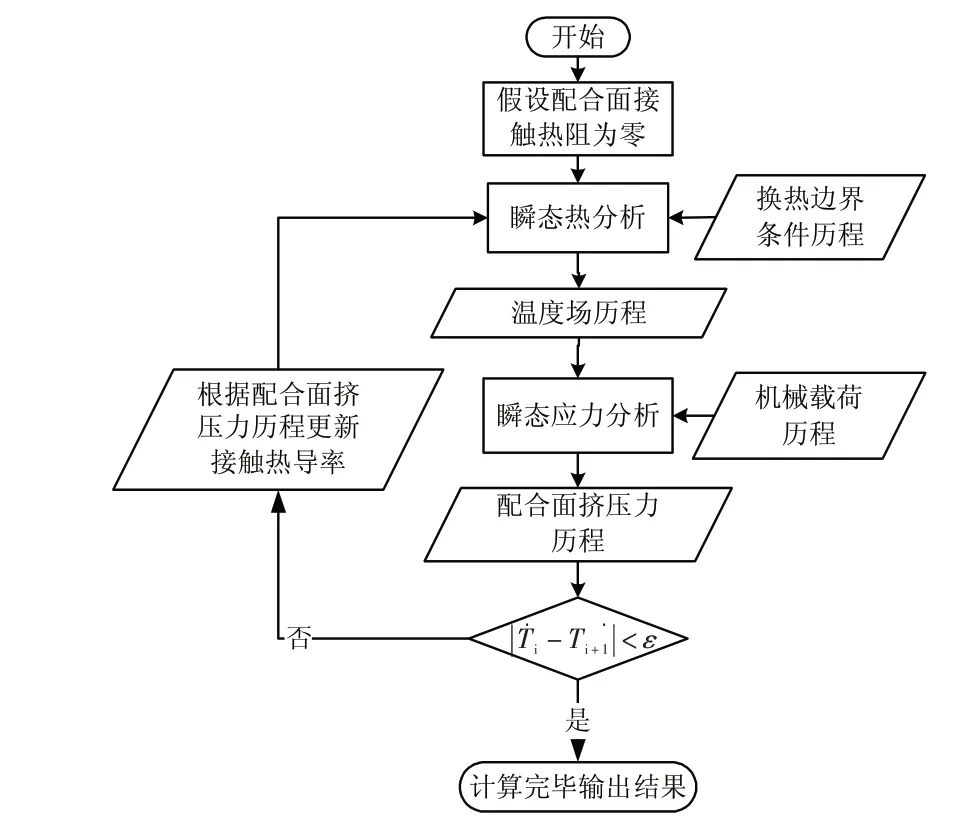
图3 过渡态响应分析流程图Fig.3 Flow chart of transient responses analysis
4 结果分析
4.1 过渡态温度场
根据有限元迭代计算得到的加减速试车历程涡轮转子温度场,绘制了无螺栓挡板平均温度与对应半径区域轮盘轮缘间(图1 中R1与R2之间部分)的平均温度变化曲线(图4)。可见,由于无螺栓挡板为薄壁结构,其热惯性与涡轮盘相比较小,所以过渡态下无螺栓挡板在加减速过程中的热响应明显比轮盘的快,特别是连续加减速过程表现得更加显著。加速过程无螺栓挡板平均温度比涡轮盘轮缘高,减速过程无螺栓挡板的平均温度比涡轮盘轮缘低。高转速停留的热平衡状态下,无螺栓挡板的平均温度比涡轮盘对应部位高。
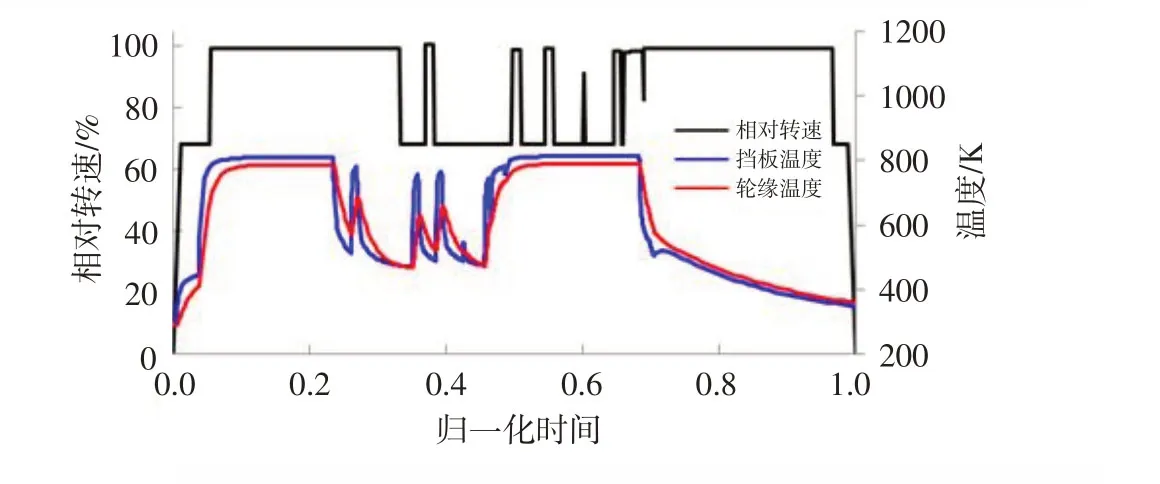
图4 无螺栓挡板与涡轮盘轮缘平均温度Fig.4 Average temperature of boltless baffle and disk rim
4.2 径向配合面挤压力
无螺栓挡板与涡轮盘径向配合面挤压力的变化历程见图5。可见,总体上径向配合面挤压力在加速过程增大,在减速过程减小,在转速停留阶段逐渐减小并趋于稳定值。加减速过渡态及稳态典型时刻的无螺栓挡板与涡轮盘径向配合面挤压力峰谷值如表1 所示。可见,在慢车状态停留一定时间再加速至最大状态后的停留阶段,径向配合面挤压力明显增大,其最大值可达稳定值的约1.6倍。结合转子加速过程中温度场变化历程特点,涡轮转子在加速过程中温度升高,但因无螺栓挡板热惯性小于涡轮盘而温度快速增加,无螺栓挡板的热变形受到涡轮盘配合面的限制,导致其与涡轮盘径向配合面挤压力显著大于稳态值。因此在无螺栓挡板设计中,应保证无螺栓挡板与涡轮盘径向配合面在加速情况下具有足够的挤压强度储备。

图5 无螺栓挡板径向配合面挤压力Fig.5 Extruding force on radial matching surfaces of boltless baffle
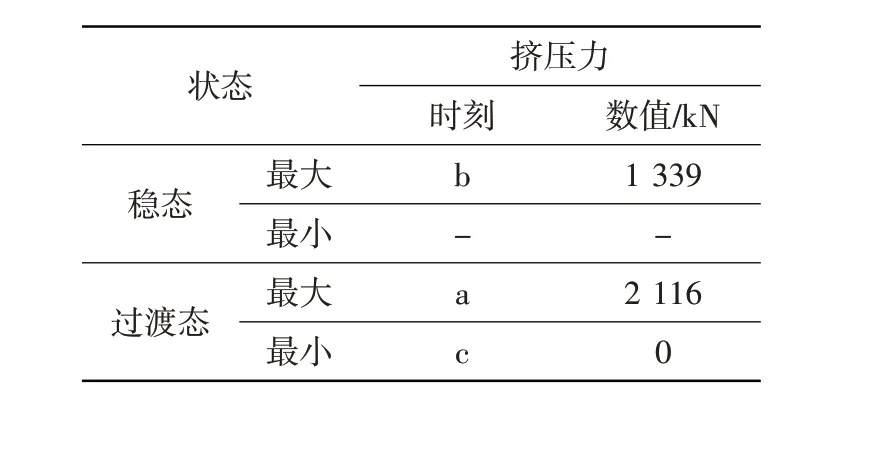
表1 典型时刻无螺栓挡板径向配合面挤压力Table 1 Extruding force on radial matching surfaces at study points
涡轮转子在最大状态达到热平衡后再快速减速到慢车状态,因无螺栓挡板热惯性小于涡轮盘而温度快速下降,其相对轮盘的负热变形使得无螺栓挡板与涡轮盘径向配合面挤压力小于稳态值,出现挤压力为零的情况,即慢车状态下无螺栓挡板与涡轮盘径向配合面产生间隙。
4.3 无螺栓挡板平均周向应力
无螺栓挡板的结构形式类似于轮盘,其工作状态下具有类似于旋转轮盘应力分布的特点,典型失效模式为周向破裂,无螺栓挡板的平均周向应力水平是衡量其承载能力的重要指标。加减速试车历程下无螺栓挡板平均周向应力变化情况见图6,其峰谷值(以无螺栓挡板平均周向应力除以材料室温屈服强度得到的无量纲值表示)情况见表2。由图表可知,最大平均周向应力不是发生在最高转速,而是发生在径向配合面挤压力为零的时刻。因此在无螺栓挡板设计中,应保证无螺栓挡板在大状态热平衡减速过程径向支撑力不足情况下的强度储备,以及无螺栓挡板此时能可靠定心。

图6 无螺栓挡板平均周向应力Fig.6 Mean circumferential stress of boltless baffle
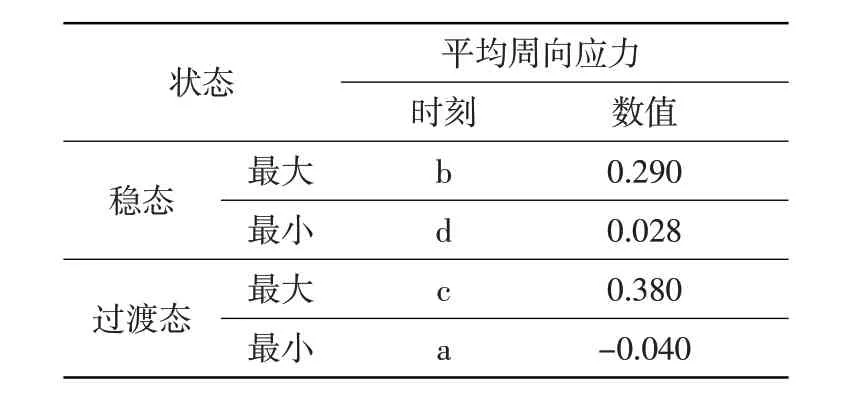
表2 典型时刻无螺栓挡板平均周向应力Table 2 Mean circumferential stresses of boltless baffle at study points
5 结论
通过航空发动机加减速试车历程中涡轮转子过渡态热固耦合响应分析,探讨了无螺栓挡板在过渡态加减速试车过程温度场和受力变化特点,得出以下主要结论:
(1) 发动机由慢车状态快速加速至大功率状态过程,无螺栓挡板热变形大于轮盘,导致无螺栓挡板与轮盘径向配合面挤压力显著大于稳态值,设计时应保证配合面具有足够的挤压强度;
(2) 发动机大功率状态热平衡后快速减速至慢车状态过程,无螺栓挡板与轮盘径向配合面挤压力快速减小,甚至形成径向间隙,此时应保证无螺栓挡板具有足够的强度储备以及工作定心。
