关于变上限积分函数及其可导性的研究

黄娟霞

变上限积分函数是数学分析中比较重要且较为复杂的一类函数，是定积分基本公式的理论基础，是沟通微分学与积分学之间的桥梁，也是应用非常广泛的一类函数［1-3］.而变上限定积分的求导是研究变上限定积分的关键，它有不同于一般函数求导的独特之处.涉及变上限积分函数的相关问题往往有一定的难度，解决起来较为困难［4-5］.因此，本文在以往研究的基础上，给出了变上限积分函数在求极限及求导等几方面的应用，依此阐述相关问题的解决方法.

1 预备知识

定 义1［5］设 函 数f(x) 是 定 义 在 闭 区 间[a,b]上的连续函数，x为闭区间[a,b]上的任意一点，当x在闭区间[a,b] 上任意变动时，对于每一个确定的x值，都有一个与之相对应，因此可看作自变量为x的函数，称为变上限积分函数，记作Φ(x)=

定理1［6］设函数f(x) 在闭区间[a,b] 上连续，则函数在闭区间[a,b]上可导，且其导函数为f(x)，即

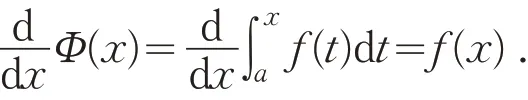
推论2［7］设函数f(x) 在闭区间[a,b] 上连续，且函数u=φ(x) 在点x处可导，则函数在闭区间[a,b] 上可导，且其导函数为

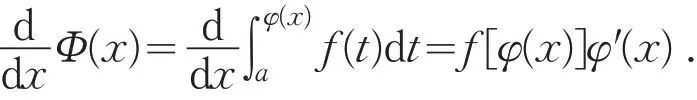
推论3［7］设函数f(x) 在闭区间[a,b] 上连续，且函数u1=φ1(x) ，u2=φ2(x) 在点x处均可导，则函数在 闭 区 间[a,b]上可导，且其导函数为

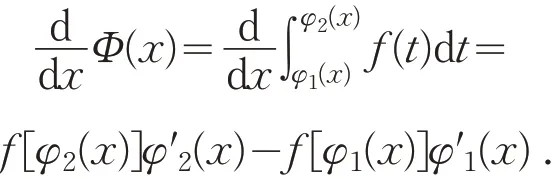
定理2［8］如果函数f(x) 在闭区间[a,b]上连续，且函数F(x) 是函数f(x) 的一个原函数，则有

2 变上限积分函数可导性的应用

2.1 极限问题

在许多求极限的问题中，往往涉及变上限积分函数的求导运算，而且经常与等价无穷小代换方法结合使用.这几类问题融合在一起，给函数极限的求解带来了较大难度.

解 由于f(t)=sint2在闭区间[0,x] 上是连续函数，根据定理1，得

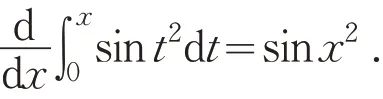
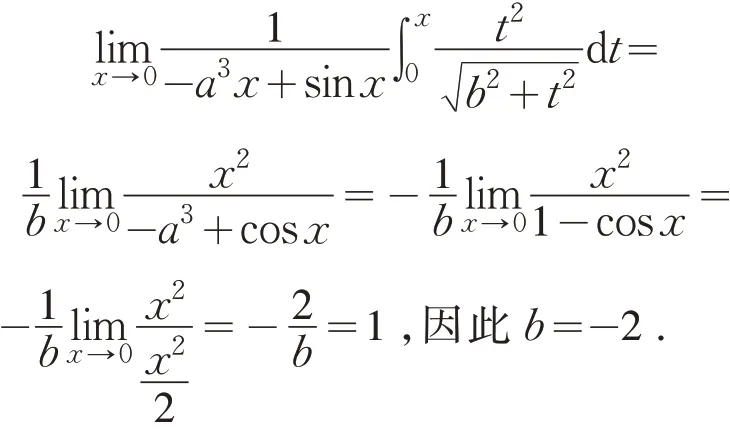
2.2 极值问题

函数的极值问题是分析学中重要且较难的问题之一，变上限积分函数由于情况复杂，难度较大，因而关于它的极值问题更是晦涩难懂.例4 求函数的极值.

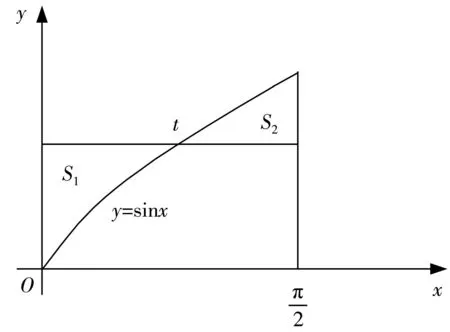
图1 由sinx 围成的封闭面积S1 及S2

令S=S1+S2，则于 是，令得驻点为.由 于 当时，，因 此 可 知为函数S的极小值点，极小值为

从上面的求解实例可以看出，在函数求极值问题中，当遇到变上限积分函数时，往往需要先对其形式进行变换，这里也涉及对积分变量进行代换，变换后符合变上限积分函数求导定理的要求时，再对其进行求导，如果不注意对变上限积分函数真正的形式的区别，很可能会得出错误的结论.

2.3 求导问题

求导问题也称为求微分问题，这类问题是数学分析中比较基础且又比较重要的一类问题.它会随着函数复杂程度的增加求导难度也加大.变上限积分函数作为一类特殊的函数，应用较为广泛，对它进行求导也尤为重要，但因其形式复杂，不易求解，因此有必要对其通过实例求解进行方法探究，更好地总结对其求导的各种方法，以便为这类问题的解决提供一定的参考.

解

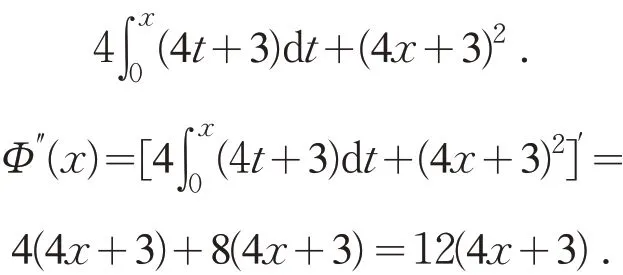
例7 设函数f(x) 为连续函数，且满足，其 中，a≠0,b＞0，求函数f(x).

根据题意易知f(0)=0 ，由（1）式可知f′(0)=a，因此要求函数f(x)就转化为求解满足初始条件f(0)=0 和f′(0)=a的二阶微分方程f″(x)-f(x)=aex的解.

此二阶微分方程的通解为f(x)=C1ex+将初始条件代入其中，得，从而

通过此题可以看出，求解未知函数解析式时，当未知函数中仍然含有函数的积分时，常将等式两边分别求导，将其化为不再含有积分的式子.

例8 设 函数，试 求

解 令u=x+t，则当t=0 时，u=x，当t=x时，u=2x，从而原函数可化为f(x)=从 而

解 函数f(x)可化简为

当x≤0 时

当x≥2 时

当 0 ＜x＜2 时

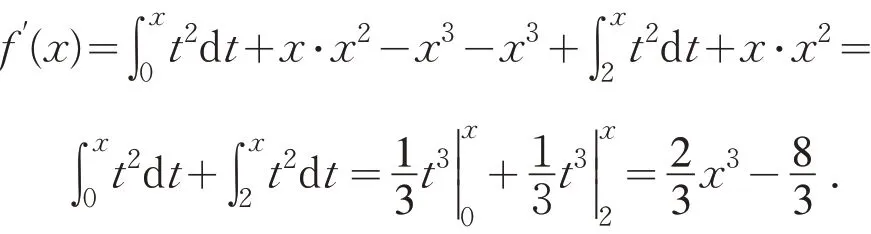
通过上面的例题可以看出，变上限积分函数，当积分上限是单独一个自变量时，可以直接应用定理1 对其进行求导.当积分的上限是自变量的函数时，此时对函数求导即为变上限积分函数的复合求导，可以按照复合函数求导法则进行.另外，如果一个含有自变量的函数与变上限积分函数乘积后求导，可以将其看作是两个乘积函数的求导，可按照乘积函数的求导法则进行，遇到变上限积分函数时，再按照变上限积分函数求导定理进行即可.当遇到被积函数的自变量中有积分变量，同时积分上限又有积分变量的情况时，这类问题在对函数求导前需要对被积函数进行变量代换，待积分变量换为新的变量时，再对变换后的新的变上限积分函数进行求导即可.

3 结论

本文针对数学分析中比较重要的一类函数——变上限积分函数进行了研究，给出了该类函数在求极限、求极值和求导等几方面的应用，从中不难看出，变上限积分函数是由于积分上限的变化而生成的函数，该函数较为复杂，而且涉及这类函数的问题应用范围较广.因此，凡是涉及该类函数的相关问题都是比较难于解决的问题.本文提到了几种变上限积分函数的实际问题，除此之外，还有一些变上限积分函数的实际问题没有提到，这类问题有待于今后进一步深入探究.