数学文化融入大学数学类课程的途径与方法

2020-06-19宋元凤华贞芝

通化师范学院学报 2020年6期

宋元凤，华贞芝

数学是研究空间形式和数量关系的学科，是刻画自然规律和社会规律的科学语言和有效工具.数学作为一个学科、一种文化，有着悠长的发展史，而在这一悠长的发展过程中，积累了许许多多前人的智慧和努力、经验和教训、成果和方法.狭义的数学文化是指数学的思想、精神、方法、观点、语言以及它们的形成和发展.广义的数学文化除上述内涵以外，还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系，等等［1-2］.国内外许多数学研究者对数学类课程中融入数学文化进行了诸多研究并取得了许多成果.南开大学顾沛教授致力于研究与宣讲数学文化在数学类课程中的作用并且撰写了专著《数学文化》［3］.徐利治教授与李尚志教授等学者也研究了数学文化，并为数学文化融入数学类课程提供理论支撑.齐民友教授与邓东皋教授在他们撰写的《数学与文化》一书中从多种角度论述数学作为一种文化对现代文化的影响和力量.2001 年颁发的《全日制义务教育数学课程标准》中特别指出，编写数学教材时要加入介绍相关数学背景知识的内容，强调数学课程中讲解数学知识时要尽量阐述相关数学史、数学发展与数学应用.近些年，许多大学与中小学都将数学文化融入到数学类课堂，通过这种途径提升学生们的数学素养.国外许多数学工作者也研究了数学文化的意义和作用，以及如何把数学文化融入到数学类课程中.1989 年，美国在课程与评价标准中明确了培养学生的目标是把学生培养成具有良好数学素养的工作者；1995 年，英国把培养学生学习数学与应用数学的信心编入国家数学课程标准；1999 年，日本在高中数学课程中加入了人类和数学之间的活动介绍，以及人类在社会生活中的数学观察和统计等内容，在学习指导纲领中，特别强调把数学文化融入数学课程的重要性；2000 年，新加坡号召要培养学生欣赏数学美的能力，激励学生应用数学的信心，鼓励学生要有解决问题的毅力.综上可见，许多国家已把数学文化融入到了数学教育中.这些国家的教育部门、机构和科研院所都在不断深入研究把数学文化融入到数学类课程中，并取得许多成果.

笔者所教授的大学数学类课程中，适当地融入了数学文化的内容，确实增加了课堂教学的趣味性，提高了教学效果，提升了学生的人文素养.

1 将数学文化融入大学数学类课程知识模块

数学史、数学悖论、数学美、数学的思想、数学的精神、数学的方法是数学文化的重要内容，适当地把这些内容引入到数学类课程中，会对学生的培养起到积极的作用.

为了改变大学数学类课堂教学枯燥和缺乏趣味的现状，提升课堂教学的趣味性；为了帮助学生构建数学知识架构，改进学生的数学知识体系；为了对学生进行行之有效的思想品德教育，培养学生良好的道德观念，提升学生的人文素养，教师可以在大学数学类课程中融入数学文化，学生的理性思维能力将得到很大的提升与改善.学生通过学习数学文化接受数学思想和方法时，思维的逻辑性、严谨性和条理性将得到锻炼，学生的人格将得到提升.

学生通过上网查阅与搜集资料，完成教师布置的课下任务.通过学习通APP 做任务、阅读、讨论、交流与书写研究报告等活动，了解人类社会发展的过程和数学发展进程以及它们之间的相互关系，了解数学规律与数学的美，了解数学在科学研究和现实生活中的广泛应用，教师在讲课之前通过讲数学家的小故事提高学生学习数学的兴趣，开阔学生视野.学生学习了数学史，了解了数学的起始与发展的历史轨迹，激发自身的创新意识，学习和领悟数学的美学魅力，培养了体会和欣赏数学美感的能力.在课堂上，教师通过播放生活和科学视频，展示图片与PPT，使学生学习和感悟数学的人文价值、应用价值、科学价值.在讲解和探讨知识的同时，讲述数学的语言、数学的观点、数学的思想、数学的方法、数学的精神，促进学生对数学知识的掌握，提高其数学人文素养，促进学生良好人格品质的形成，为学生的发展打下坚实的基础.

1.1 将数学史融入大学数学类课程知识模块

在大学数学类课程中适当融入数学史知识，可以使学生尽快理解、消化所学知识，培养学生数学的思维品质，能够适时对学生进行德育教育，提升学生的人文素养.

在讲授向量代数中标架与坐标时，由数学史引入这节知识.费马与笛卡尔在几何中引入了坐标系，但他们引入的坐标系没有负坐标，坐标系是平面斜坐标系.Van Schooten 在两位数学家的基础上，引入负的横、纵坐标.在费马与笛卡尔的三维空间解析几何的思想之后，约翰·伯努利最先引入了空间直角坐标系.从几何的二维坐标系到三维坐标系的引入，大约用了四十多年，可见一个理论的形成、发展与完善是需要很多数学家持之以恒的探索与研究的.通过这段数学史的介绍，让学生认识到学习需要持之以恒，勤动脑多思考.在讲述这部分知识时还可以把坐标系的知识和思想政治教育结合起来，培养学生的人文素养.

讲授极限概念时，教师可以引入我国数学家刘徽提出的“割圆术”，刘徽描述他的“割圆术”为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”［4］.教师可以利用动画演示刘徽的“割圆术”，动画演示从圆内切正六边形开始，依次添加正十二边形，正二十四边形，……，圆的内切正多边形边数越多，正多边形的面积与圆面积的差距就会越小，把极限过程演示得十分生动和具体.通过这种方式帮助学生了解和认识到我国古代数学文化在当时处于世界领先水平，弘扬中国数学文化，让学生产生国家和民族荣誉感，同时调动学生学习数学的积极性，奋发图强，为中国的现代化建设贡献自己的力量.

在讲授初等数论课程时，同余这部分知识与中国剩余定理是紧密相连的.中国剩余定理又称为孙子定理，最早出现在公元5 世纪中国南北朝时期的数学著作《孙子算经》里，其内容是“有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？即一个整数除以三余二，除以五余三，除以七余二，求这个整数”［5］.该定理是中国古代求解一次同余式组的方法，是数论中的一个重要定理.通过讲授中国剩余定理，使学生了解同余知识的起源，同时使学生了解中国剩余定理是中国古代历史上最完美和最值得骄傲的数学成果之一，它是中国对世界数学的重要贡献，通过讲授这些内容来增加学生的学习兴趣和民族自豪感.

在讲授高等代数课程的二次型知识时，由于这部分内容比较抽象且不好理解，可以讲授二次型引入的背景和历史，使学生知其然，也知其所以然.二次型的研究开始于18 世纪对二次曲线与二次曲面的分类问题.高斯引入了二次型的正定、负定、半正定和半负定等概念；柯西首先开始研究二次型的分类；西尔维斯特给出了n个变数的二次型的惯性定律；雅克比重新发现和证明了上面的定理；维尔斯特拉斯给出了同时化两个二次型成平方和的方法.

1.2 将数学悖论知识融入大学数学类课程知识模块

数学悖论是基于人类对客观事物的认识的基础上，提出的逻辑矛盾的数学结论.数学悖论是数学发展历史进程中出现的一种文化，是数学文化的重要组成部分.课堂教学中引入数学悖论，可以提高数学类课程的趣味性，提高学生的思维能力，激发学生探索科学的兴趣.

在一些大学数学类课程的课堂上讲授一些和这个学科相关的悖论，可以激起学生的学习兴趣，激发学生的求知欲.秃子悖论内容是“若一个人有X根头发，被称为秃子，则有X+1 根头发的人也是秃子，因此(X+1)+1 根头发的人还是秃子.以此递推，会得到结论无论你有多少根头发你都是秃子”，这个悖论是模糊数学中的经典悖论“.飞矢不动”悖论是由芝诺提出的，其内容是：“由于箭在它的飞行途中任何瞬间都有一个暂时的位置，因此它在这个位置上和静止没有什么区别.”这是数学分析课程中关于连续性知识的一个悖论.罗素悖论是由罗素提出的，其内容是：“对于任意一个集合A，A要么是自身的元素，即A∈A；A要么不是自身的元素，即A∉A”［6］，这是集合论的一个悖论.而“理发师悖论”是罗素悖论通俗化的一个悖论，“理发师悖论”的内容是“一个理发师声称将给城里所有不给自己理发的人理发.”根据理发师的声明，他到底是否应该给自己理发呢？根据这个悖论，他给不给自己理发都是不对的，因此这是一个悖论.通过讲述悖论可以挖掘学生的探索欲和求知欲，引导学生形成严谨的思维.

1.3 将数学美融入大学数学类课程知识模块

数学美体现在许多方面，比如公式的简洁美，图形的对称美和图形美，数学的语言美等.大学数学教师在讲授数学类课程时应该考虑把数学美的教育融入到课程中，使学生感悟和欣赏数学之美，同时能够培养学生创造美的能力.

在讲授解析几何的单叶双曲面知识时，先介绍单叶双曲面的对称性，即单叶双曲面关于坐标原点、三个坐标面、三个坐标轴对称.然后通过单叶双曲面在建筑物、工业中和生活中的应用，例如广州电视塔（图1）、上海世博会的太阳谷（图2）、日本的神户塔（图3）、花瓶等了解单叶双曲面是对称的、优美的、有用的，从而促使学生认识到单叶双曲面的知识是有应用价值的，也使学生从中体会到数学的美感.

图1 广州电视塔

图2 上海世博会的太阳谷

图3 日本的神户塔

在讲授高等代数的线性空间知识时，数域p上线性空间V有一个关于线性空间的维数定理.

定理1 如果V1,V2是线性空间V的两个子空间，那么

维（V1）+维（V2）=维（V1+V2）+维（V1⋂V2）.

在讲述线性方程组知识时，把线性方程组

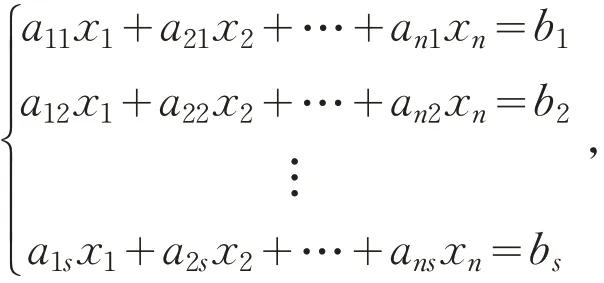
写成矩阵的形式AX=B，充分体现了数学的简洁美.

通过前面的两个例子可以看到数学的简洁美，这样的结论在大学数学类课程中比比皆是，在讲授这类知识时，教师可以有意识地传播这些思想，使得学生感受数学的简洁美，并能够欣赏和领悟这种美.

1.4 将数学的思想、精神、方法融入大学数学类课程知识模块

数学的思想包括归纳思想、极限思想、代换思想等，数学精神包括探究精神、质疑精神等，数学方法包括尝试方法、类比方法、代换方法、归纳方法等.数学的思想、精神、方法是数学文化必要的组成部分，教师在讲授数学知识的同时，更应该注重传授数学的思想、精神、方法，锻炼学生的思维和解决问题的能力.

在讲授概率论课程的知识时，可以引进一些机会游戏的计算、抽彩中奖问题的研究、人身保险问题的研究，阐述概率论的应用，引入所学知识，培养学生的数学思想，锻炼学生的数学精神，改善学生的数学方法.

在讲授解析几何课程二次曲面的知识时，可利用平行截割法根据整体观察截痕的变化规律来了解和认识单叶双曲面的形状.研究和认识二次曲面形状的基本办法是平行截割法.为了弄清楚曲面的大致形状，进而推出它的性质，通常把曲面作为点的轨迹来研究，而分析一组平行平面去截割图形会得到一组平面截痕，通过一组平面截痕的变化规律来研究图形整体形状，即部分的变化规律来研究图形整体形状，从这个方法我们可以体会出由部分到整体、由特殊到一般的认识事物的办法.通过这部分知识的讲解，使学生认识和学习到数学的思想和数学的方法.