空间解析几何中直线参数方程的教学反思
2020-06-19徐传友
徐传友
自笛卡尔和费马[1]研究出图形与坐标的关系以后,求动点的轨迹方程时,直接找出给定条件动点的坐标x,y,z之间的关系式很困难,但如果适当地引入一个辅助变量(称为参数),则较容易找出坐标x,y,z和参数之间的关系式,即得到了图形的参数方程,这样就间接地建立了x,y,z之间的关系式.
参数方程不仅是空间解析几何的一个重要研究内容,而且在数学分析中的二重积分、曲线积分、曲面积分中也有重要应用[2],与微分几何联系紧密[3],在电脑美术设计中也有广泛应用[4].
1 曲线参数方程的概念
如果变数t(a≤t≤b)的每一个值对应于变向量r→的一个完全确定的值r→(t) ,则称r→=r→(t)是t的向量函数.在直角坐标系向量函数可以写成r→(t)=x(t)→i+y(t)→j+z(t)k→.
定义1[5]取t的一切可能取的值,向量函数表示的向径终点总在一条曲线上;反过来,在这条曲线上的任意点,总对应着以它为终点的向径,而这向径可由t的某一值t0(a≤t0≤b)通过向量函数的表达式完全决定,那么就把向量函数表达式叫作曲线的向量式参数方程.
2 直线参数方程的应用
在空间解析几何课程的教学中,直线可谓是贯穿始终.既可以直接利用直线的参数方程研究直线与直线、直线与平面的相交和垂直的问题,直线与二次曲面的相交、相切的问题,以及二次曲面的相交、相切的问题,还可以给出教材[5]中某些结论的重新证明.
2.1 相交方面的应用
在考虑直线与直线、直线与平面和二次曲面相交,或者二次曲面之间相交的时候,使用直线的参数方程比较便捷.
例1 求过点P(1,-1,1) 且与直线垂直相交的直线.
解 已知直线的方向向量v→=(2,1,-1),且过点(-1,-1,0) ,所以直线的参数方程为x=-1+2t,y=-1+t,z=-t,因此所求直线与已知直线的交点坐标可以写为Q(2t-1,t-1,-t),因此,且向量与已知向量v→垂直,则有2(2t-2)+t-(-t-1)=0,解得,所以直线的一个方向向量w→=(2,-1,3) ,其标准方程为
本题也可以使用常规方法求解,但过程相对复杂.下面给出常规解法.

又由于两直线相交,所以假设交点坐标为M(p,q,r).一方面,点P和点M都在所求的直线上,所以向量与向量共线,因此得到另一方面,点M在已知直线上,所以点M的坐标满足已知直线的方程,即

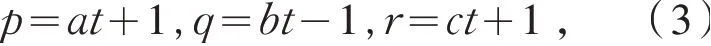

由式(1)和式(4),解得a:b:c=2:(-1):3 ,因此所求直线的标准方程为
教学反思:从例1 的两种解法容易看出,在解决直线的相交问题时利用参数方程步骤简洁,解题思路更加清晰.在教学过程中,如何引导学生使用参数方程很关键.在与例1 类似的问题中,需要学生抓住关键词“相交”,然后利用参数方程给出交点坐标,进而再利用相关条件解决问题.
当两个球面相交时,交线是圆,如何得到圆心呢?此时圆心在两球心的连线上,于是可以利用直线的参数方程将其表示出来,再结合其他几何知识就可以求出圆心坐标.
例2 假设两球面(x-1)2+(y-1)2+(z-2)2=4 和(x+1)2+(y-2)2+z2=9 相 交,求 其交线圆的圆心.
解 两球心分别为O1(1,1,2) ,O2(-1,2,0),两球半径分别为R1=2 ,R2=3.由于交线圆的圆心在两球心的连线上,且(2,-1,2) ,所以两球心的连线的方向向量可以 取其 参 数 方 程 为x=2t+1,y=-t+1,z=2t+2 ,所以圆心C的坐标为C=(2t+1,-t+1,2t+2) ,设圆的半径为r,利用圆半径和球半径的关系,可得解得t=因而可得圆心C的坐标为
教学反思:解决本题的关键是知道相交圆的圆心在两球心的连线上,且该连线与相交圆所在平面垂直,这样就可以将求圆心问题转化为求直线问题上来.
通过上述两个例子可以看出,只要问题中直接或间接给出直线内容,就可以使用直线的参数方程来解决.
2.2 距离方面的应用
解析几何教材给出了点到平面、点到直线以及两异面直线之间的距离公式[5].具体公式如表1 所示.
事实上,教材中所给的三种距离的定义都是最短距离,从分析的角度出发,这个最短距离是得到的距离函数的最小值,因此,可以利用直线和平面的参数方程重新求出上述三种距离公式.
性质1 点P(x0,y0,z0) 到直线的距离为,其 中
证明 直线L过点M(α,β,γ) ,方向向量为,其参数方程为bt+β,z=ct+γ,根据点到直线距离的定义,需要求出点P与直线上所有点的距离,并求出最小值,即求出距离函数的最小值,因此有这是关于参数t的一元二次函数,它的最小值为ρ=即为原来点到直线的距离公式.
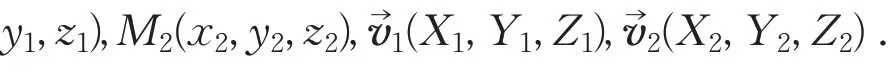

表1 距离公式
注1:由上述证明过程可以看出在L1上存在唯一一点P,在L2上存在唯一一点Q,使得PQ的距离最短,即为异面直线的距离.另 外,,即PQ所在直线与直线L1垂直,同理可得PQ所在直线与直线L2垂直,因此可得如下结论:
性质3 两异面直线的公垂线存在且唯一.
注2:与上述的推导类似,可以得到点到平面的距离.
教学反思:教材中虽然已给出距离公式,但在教学过程中,给出上述的推导过程,一方面可以帮助学生更形象地理解书中距离的定义,即最短距离.另一方面也可帮助学生掌握数学分析中极值的求法,并且当需要求垂足问题时,使用上述方法比较简单.
2.3 相切方面的应用
定义2 从二次曲面S外一点向曲面引切线,则这些切线生成的曲面称为切锥面.
特别地,如果曲面S是球面,则切锥面是圆锥面.
例3 给定椭圆抛物面S,方程为z=3x2+4y2+1,求以原点O为顶点的切锥面方程.
解 设M(x,y,z) 是切锥面上的任意一点(非原点).则直线OM上存在唯一的切点N,即存在唯一的实数t,使得(tx,ty,tz)是该切点N的坐标,由于切点M(x,y,z)在椭圆抛物面上,所以其坐标满足椭圆抛物面的方程,即tz=3(tx)2+4(ty)2+1,整理得(3x2+4y2)t2-tz+1=0 ,这是关于t的一元二次方程,由相切的条件得到Δ=z2-4(3x2+4y2)=0 ,即所求的切锥面的方程为z2=4(3x2+4y2).
例4 给定椭球面S,方程为设方向为常向量v→的一束平行光线照射S,其中部分光线与S相切,它们的切点在S上形成一条曲线Γ.证明:Γ落在一张过椭球面中心的平面上.
证明 不妨设常向量v→=(α,β,γ) ,在曲线Γ上任取一点M(x,y,z) ,且M是切点,则过M的光线l(t)=(x,y,z)+t(α,β,γ) 是椭球面的切 线,其 上 任 意 一 点 坐 标 为(x+tα,y+tβ,z+tγ) .由于每条切线与椭球面有且仅有一个 切 点,故t=0 是的唯一解,由于(x,y,z)∈Γ⊂S,上述方程化为,此方程只有t=0 的唯一解,当且仅当,这是一个过原点的平面方程,故Γ落在一张过椭球面中心的平面上.
教学反思:从上面的证明可以看出,在教学过程中,涉及到相切问题,可以引导学生思考如何利用直线的参数方程,把切点问题转化为关于参数t的一元二次方程的相等实根问题.
2.4 对称性方面的应用
利用二次曲面的对称性,在求二重积分、曲面积分和曲线积分时非常方便,因此了解曲面的对称性很重要.如何判断曲面具有对称性呢?即如何知道一个二次曲面具有对称平面、对称轴和对称中心呢?这就需要先研究已知点关于点、直线和平面的对称点,然后再研究曲面的对称性.下面以点关于平面的对称点为例进行研究.
性质4 点P(x0,y0,z0)关于平面Ax+By+Cz+D=0 的对称点坐标是
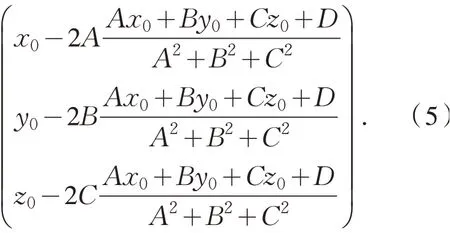
解 平面的法向量为n→=(A,B,C) ,过点P且以n→为方向向量的直线的参数方程为x=x0+At,y=y0+Bt,z=z0+Ct.此直线与平面垂直相交,把参数方程代入平面方程得(A2+B2+C2)t+Ax0+By0+Cz0+D=0 ,从 而参数则直线与平面的交点坐标为此时O点是P点和对称点Q的中点,因此对称点坐标即为式(5).
虽然空间解析几何的教材中都提到了二次曲面的对称性,即三个坐标面都是椭球面和双曲面的对称平面,三个坐标轴都是椭球面和双曲面的对称轴,原点是对称中心.而抛物面只有两个对称平面,一个对称轴,没有对称中心.这些结果自然会引起学生的思考,为什么这三类曲面的对称平面、对称轴和对称中心不同?怎么得到的这些对称平面、对称轴和对称中心?为什么坐标面是对称平面,坐标轴是对称轴呢?其他平面和直线是不是对称平面和对称轴呢?这些都没有给出具体说明,我们以椭球面为例给出具体的推导过程.
性质5 三轴椭球面有且仅有三个对称平面,旋转椭球面有无数个对称平面.
证明 不妨设椭球面的方程为
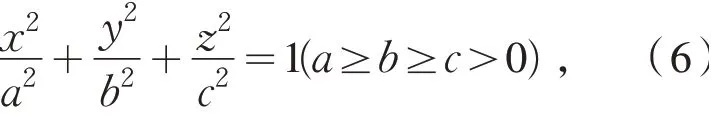
在椭球面上任取一点P0(x0,y0,z0) ,假设椭球面的对称平面方程为Ax+By+Cz+D=0 ,则点P0关于平面的对称点坐标为式(5),把式(5)代入椭球面方程,得到
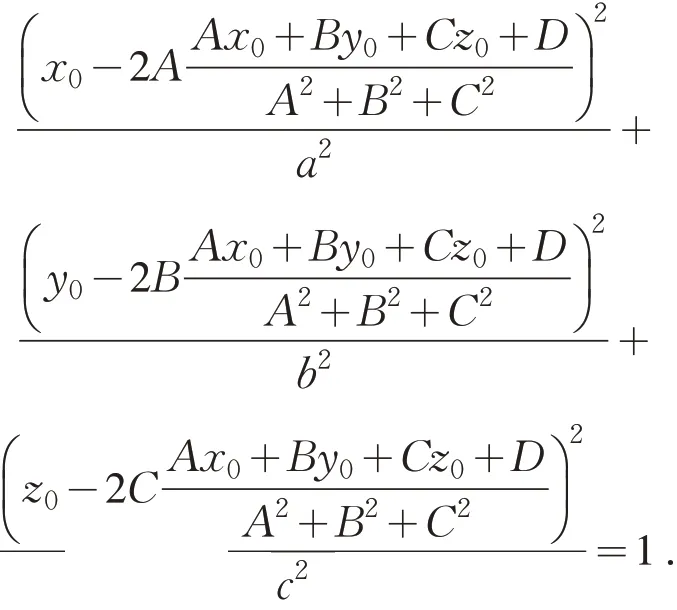
由于P0点坐标满足椭球面方程,故上述方程化为
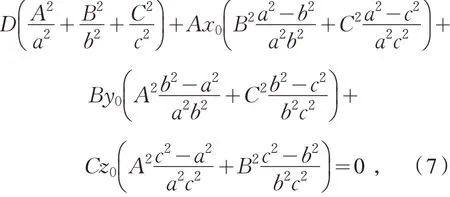
由于(-x0,-y0,-z0) 也满足椭球面方程,所以也满足式(7),代入上式得到


由于A,B,C不全为零,所以式(8)中D=0.由于(x0,-y0,-z0),(-x0,y0,-z0),(-x0,-y0,z0)也满足椭球面方程,所以也满足式(9),代入式(9)得到
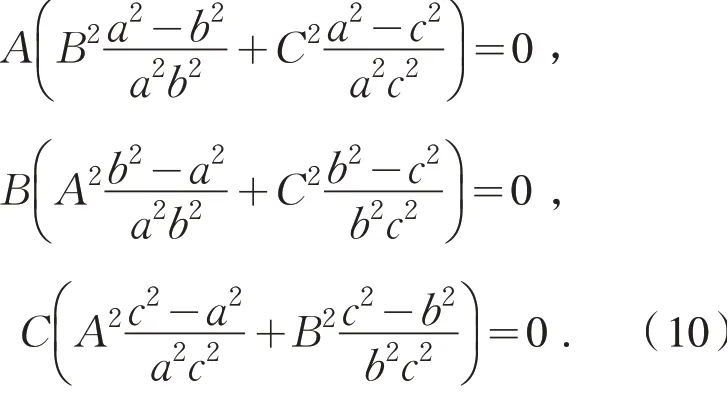
以下分两种情况讨论.
一是椭球面为三轴椭球面的情形.不妨设a>b>c.如果A,B,C全不为零,则式(10)化为
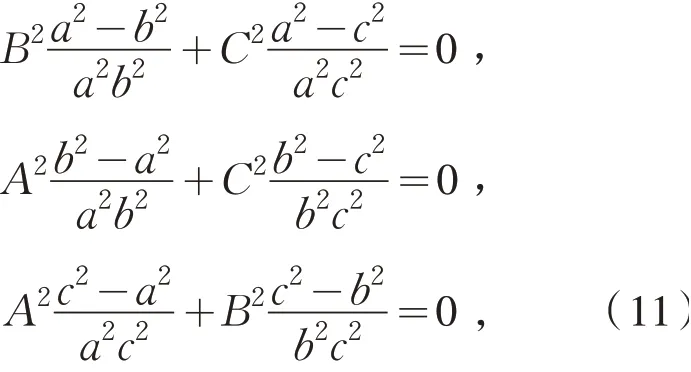
因为a>b>c,所以由式(11)得到A=B=C,这与假设矛盾,所以ABC=0.如果A,B,C中有一个为零,不妨设A=0 ,则式(10)中的第二式和第三式化为由条件可知B=0,或者C=0.其他两种假设可以类似讨论.
所以在该情形下,对称平面是X=0 ,Y=0 和Z=0 三个坐标平面,即式(6)表示的三轴椭球面有且仅有三个对称平面,且对称平面为三个坐标面.
二是椭球面为旋转椭球面的情形.不妨设a=b>c,则式(9)化为AC2=0 ,BC2=0 ,于是C=0 ,或者A=B=0.如果A=B=0 ,则对称平面为XOY平面;如果C=0 ,则对称平面为过z轴的平面,且有无数个.
如果给出椭球面的一般方程,则经过坐标变换,一般方程可以化为标准方程(6),讨论过程参考上述内容,对称平面的个数不变,只是对称平面不一定再是坐标平面,而是与坐标变换有关,这里不再赘述.
注3:对椭球面的对称轴和对称中心可以类似讨论.同理,柱面、锥面、双曲面和抛物面也都可以类似讨论.
教学反思:教材中直接说明了椭球面的对称平面问题,但是并没有说明还有没有其他的对称平面.我们在对这个知识点进行讲解时,可以引导学生考虑两个问题:①椭球面的对称平面为什么是三个坐标面,还有没有其他对称平面;②如果还有其他对称平面的话,该如何得到,然后逐渐引导学生结合点关于平面的对称点问题,利用直线的参数方程求解对称点,并考虑椭球面的对称平面问题.
通过对这些知识的挖掘,既帮助学生理解了椭球面的对称性,又能引起他们对课程内容的思考,培养学生们的科研能力,有利于提升他们以后的教学研究能力.
3 结束语
直线在空间解析几何课程中有许多应用,本文是几何教学团队多年教学经验总结的成果.这些成果立足于课本知识,又有许多延伸,可以作为学生的研究性课题.当然,空间解析几何还有许多内容可以挖掘,今后会继续加以研究.
