波形钢腹板组合连续箱梁的徐变与剪力滞效应分析

2020-06-18

福建质量管理 2020年11期

(中铁一院集团新疆铁道勘察设计院有限公司新疆乌鲁木齐 830011)

引言

波形钢腹板组合箱梁是最近几十年开始逐步使用的一种新型结构，其受力特点为弯矩主要由箱梁顶底板承担，剪力主要由钢腹板承担，与常规混凝土箱梁相比，具有节省圬工，自重较小，从而也减小了桥梁下部结构的工程量，具有良好的经济效益。混凝土有徐变，而钢材没有，从而导致混凝土和钢材连接处的应力随时间的变化产生应力重分布[1-2]，进而影响箱梁剪力滞效应的变化[3]。

唐杨[4]研究了在不同环境相对湿度、加载龄期、加载时间、混凝土强度等级以及桥墩高度对波形钢腹板组合箱梁桥收缩徐变的影响。李立峰等[5]通过对两根模型梁205d的持续监测，得出波形钢腹板箱梁能有效减少徐变引起的反拱。胡旭辉等[6]从波形钢腹板组合箱梁截面尺寸，钢腹板数量及厚度，顶底板厚度等方面对箱梁剪力滞效应的影响进行了分析计算和有限元模拟。熊锋等[7]分析研究了波形钢腹板连续箱梁施工过程中，剪切变形对徐变引起的结构挠度和应力变化程度。虽然很多国内外的学者对混凝土徐变和箱梁剪力滞问题都做了很多研究，但是鲜有人将二者综合起来考虑，尤其是在这种新型波形钢腹板组合箱梁上，故如何考虑箱梁徐变对剪力滞效应的影响并建立相应的理论分析方法是非常必要的。

一、波形钢腹板组合连续箱梁的剪力滞效应分析

利用叠加法原理，可将以图1所示的两跨连续梁分解为两个简支梁，如图2(a)、(b)所示，计算两个简支梁的剪力滞效应，然后叠加获得原连续梁的剪力滞效应[8]。

图1 两跨连续梁

(a)

(b)

对(a)，结构的剪力和弯矩为：

(1)

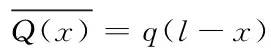
(2)

由文献[7]可得：

(3)

由边界条件u′|x=0=0,u′|x=2l=0得：

(4)

可得u(x)的表达式为：

(5)

得到图(a)的附加弯矩表达式为：

(6)

同理，得到图(b)的附加弯矩的表达式：

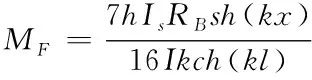
(7)

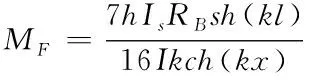
(8)

根据叠加原理，结构的附加弯矩表达式为：

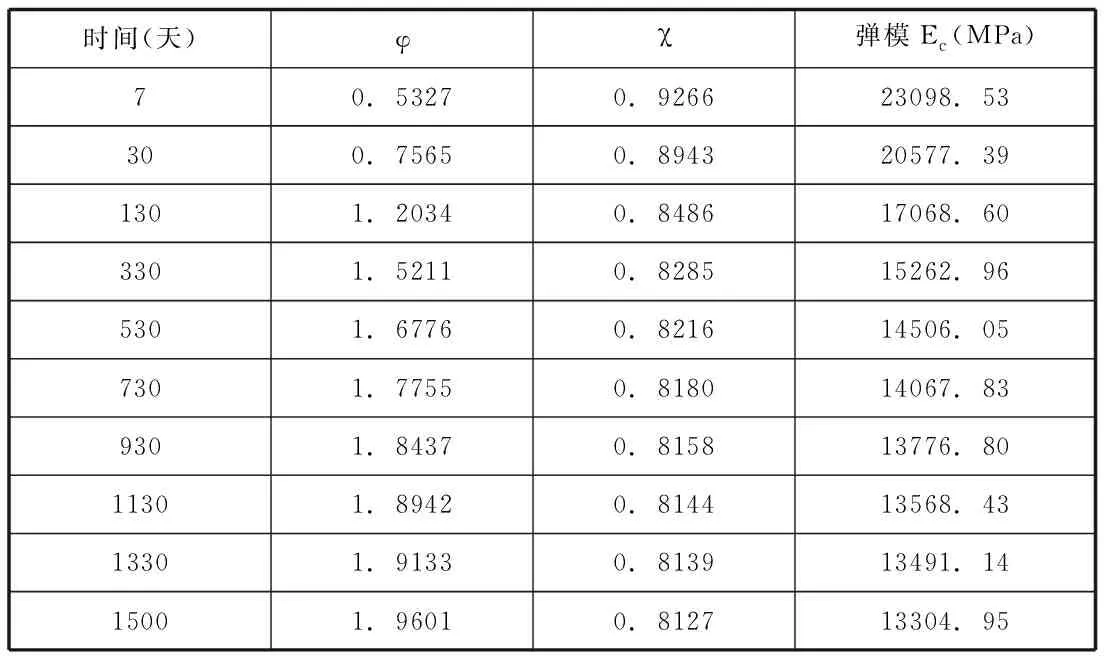
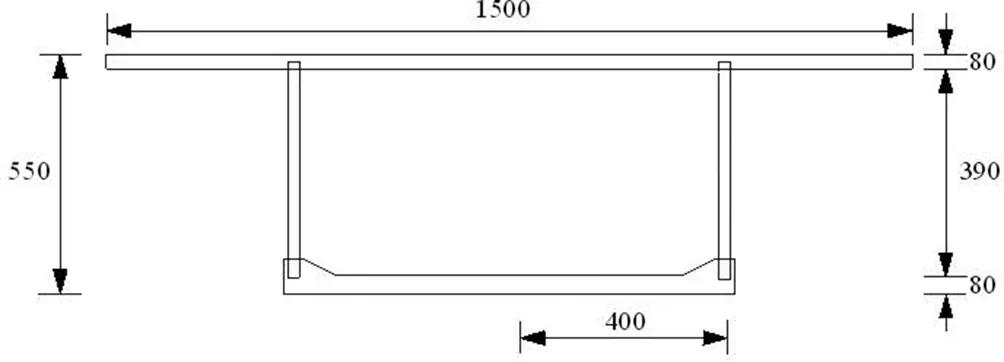
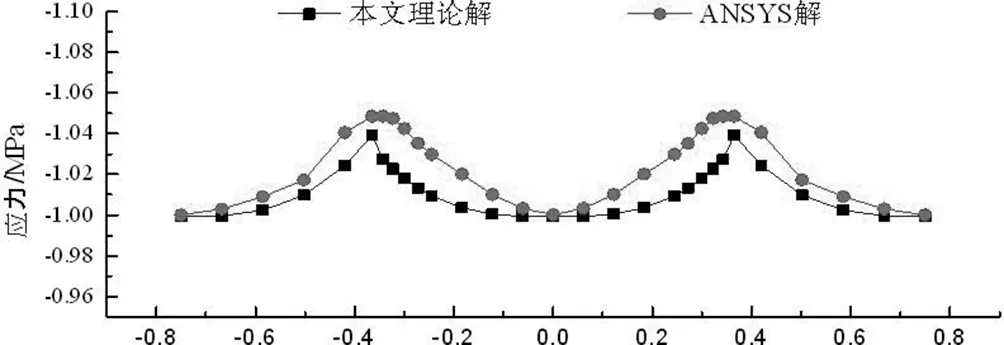
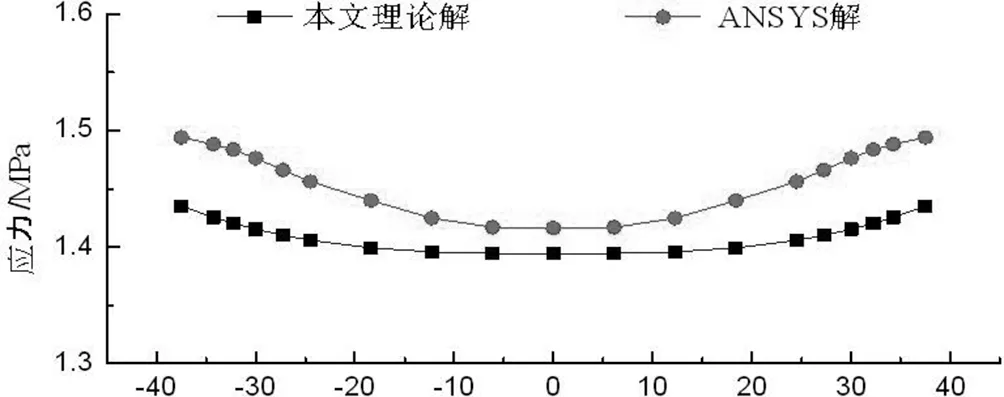
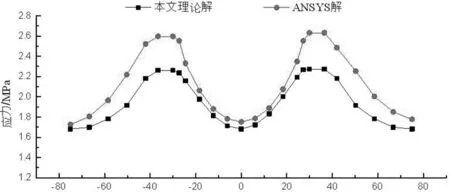
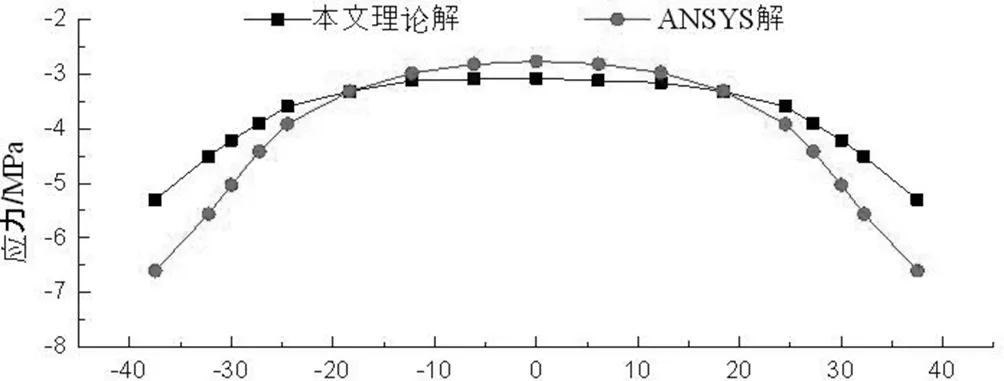
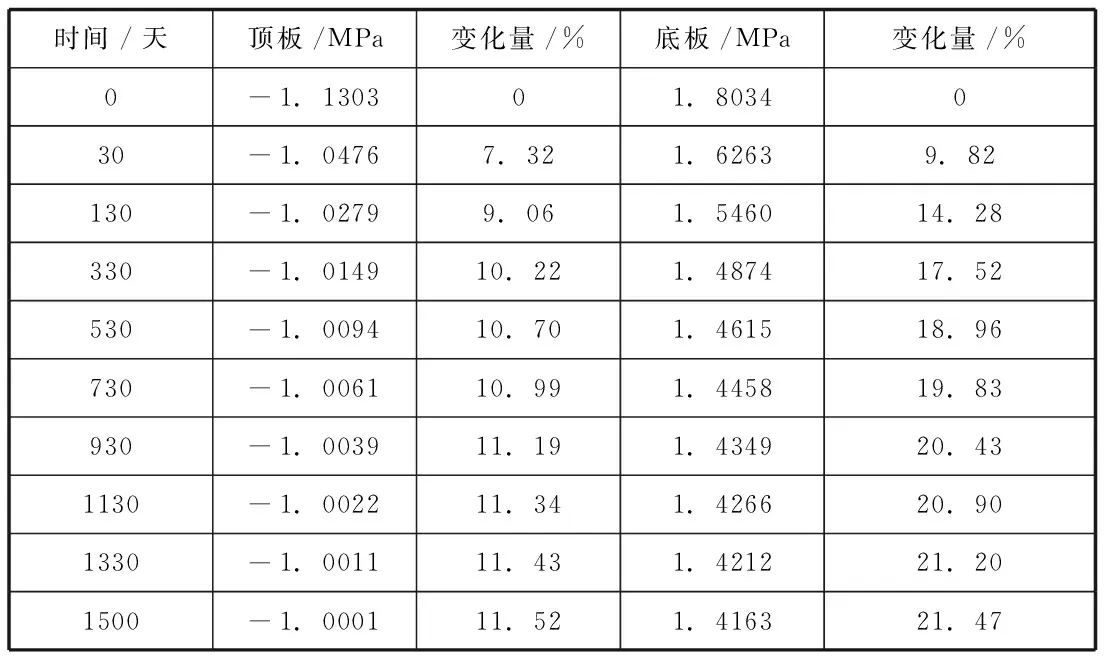
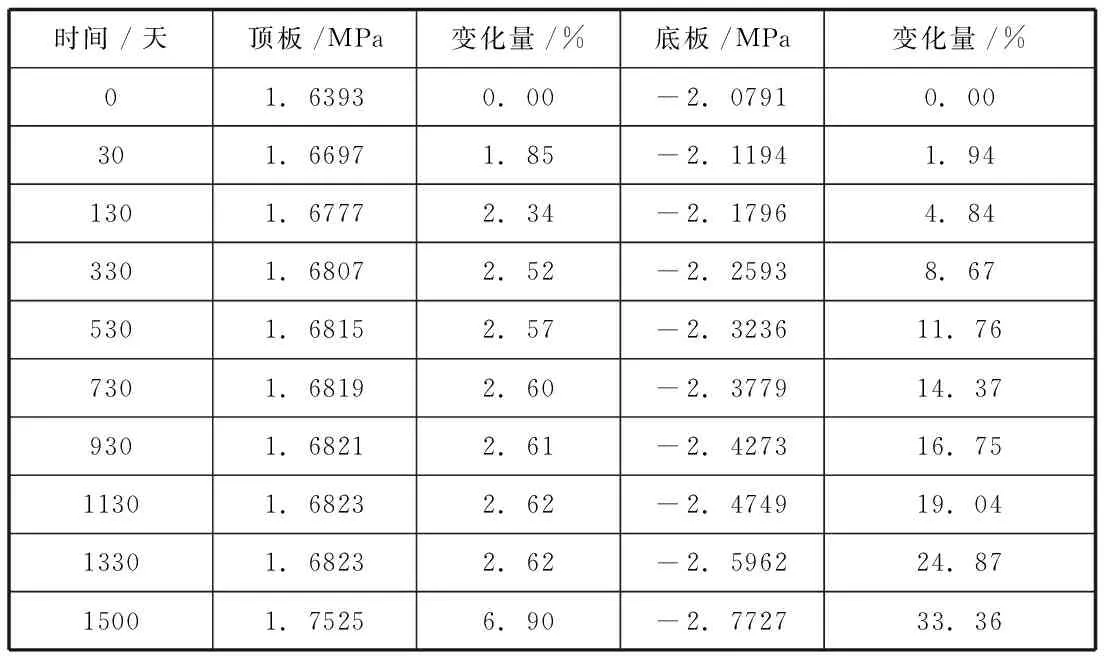
当0≤x

(9)

当l≤x≤2l时：

(10)

由文献[7]及式(7)～(10)得波形钢腹板连续箱梁翼板应力为：

当0≤x

(11)

当l≤x≤2l时：

(12)

二、徐变效应分析

Z.P Bazant[9]提出按龄期调整的有效模量法计算徐变的混凝土应力-应变关系为：

(13)

式中：t0——加载龄期；φ(t,t0)——徐变系数；

按龄期调整的有效模量为：

(14)

式中：χ(t,t0)——老化系数

将式(14)带入式(13)得：

Δσc(t,t0)=Ec(t,t0){εc(t)-εc(t0)[1+φ(t,t0)]}

(15)

任意t0时刻波形钢腹板组合连续箱梁的应力为：

σc(t,t0)=Ec(t0){εc(t)-εc(t0)φ(t,t0)[1-χ(t,t0)]}

(16)

式中，β(t,t0)=φ(t,t0)[1-χ(t,t0)]为徐变影响系数，带入上式得：

σc(t,t0)=Ec(t,t0){εc(t)-εc(t0)β(t,t0)}=σc(t)-σc(t0)β(t,t0)

(17)

(一)按龄期调整的有效模量计算

H.Trost根据CEB FIP(1964)假定徐变系数和弹性模量为不变量，老化系数χ的平均值在0.82左右，建议取0.8。实际上0.8是老化系数随着徐变时间无限增长的收敛值，H.Trost对χ取值为一不变常数，低估了徐变效应，对混凝土前期徐变效应计算会有一定的计算误差。所以本文计算了考虑老化系数的按龄期调整的有效模量：

(18)

式中：R(t,t0)——松弛系数。

王勋文[9]依据徐变系数φ与松弛函数R之间的非线性关系和对大量实验数据的分析拟合，推导得出了老化系数的计算公式为：

(19)

(20)

本文采用式(19)(20)进行老化系数的计算，运用T-B方程计算波形钢腹板组合连续箱梁的徐变效应，模型中混凝土的不同时刻的按龄期调整的有效模量如表1所示：