尾部风险视角下的投资组合优化

周 亮

(1.湖南财政经济学院 财政金融学院，湖南 长沙 410205；2.湖南师范大学 数学与统计学院，湖南 长沙 410081)

一、引言

马科维茨的均值—方差模型(M-V模型)奠定了现代投资组合理论的基石，但随着风险定义的变化，导致了投资组合构建问题的不断修正。Bertocchi等研究表明，通过经典的均值—方差框架构造的投资组合可能缺乏最优性，未能正确识别出资产收益率的非正态分布对风险产生的影响[1]。金融资产收益率往往表现出尖峰厚尾及负偏的非正态分布特征，因此采用方差来对资产的风险进行衡量并不完全准确，Sortino和Price采用下行标准差来衡量资产风险，并用其代替标准差对经典的夏普比率进行修正，提出了Sortino比率，即用超额收益率除以下行标准差来衡量资产的风险调整后收益[2]。下行标准差仅将资产收益率下跌的部分看作风险，而收益率上行的部分不作为风险，更为符合人们的心理预期。随后，Alexander和Baptista在Sortino比率的基础上更进一步，利用在险价值(Value-at-Risk，VaR)对夏普比率进行了再次修正[3]。VaR是由JP摩根公司在1994年提出的，在既定概率水平下，某投资组合在某段时间内可能产生的最大损失，VaR简单明了，可以对金融资产的尾部风险进行有效的度量，因此自提出以来在理论研究和金融监管层面得到了极其广泛的运用[4-5]。

但是VaR不满足凸性和次可加性，不是一致性风险度量指标，即用VaR来作为风险衡量指标时，投资组合的风险不一定小于各项资产风险中的最大值，这不符合风险分散化的市场原理和经济意义。因此，Rockafeller和Uryasev提出了条件在险价值(Conditional Value-at-Risk，CVaR)，指的是投资组合的损失超过某个给定VaR值的条件下，该投资组合的平均损失值[6]。CVaR可以对投资组合的尾部风险进行更准确的刻画，且满足次可加性、正齐次性、单调性和平移不变性，是一致性风险度量指标[7]，因此CVaR在理论和实践层面都得到了广泛应用[8]。很多学者通过用CVaR指标代替标准差来改进马科维茨的MV模型，或对夏普比率进行改进。如Alexander分析了衍生品投资组合构建过程中的CVaR最小化模型投资绩效[9]；Gao等比较了均值—CVaR模型与均值—下行波动率模型在构建投资组合时的绩效表现差异[10]；康志林和李仲飞讨论了大样本或者大规模投资组合下均值—CVaR模型的最优化求解方法[11]；黄金波等则使用CVaR替代了夏普比率中的标准差，构造了用来测度基金业绩的修正夏普比率[12]。本文在构建尾部风险投资组合时，将利用CVaR构造风险最小化模型，同时采用黄金波等构造的修正夏普比率对组合绩效进行衡量。

除CVaR外，高阶矩也是衡量尾部风险的常用指标[13]，如当资产收益率序列偏度更小及峰度更大时，说明资产的尾部风险更高。Samuelson指出，在资产组合的随机收益不服从正态分布或者投资者的效用函数不是二次函数的情况下，高阶矩风险不能忽略不计[14]。一些学者开始对高阶矩组合投资问题进行了研究。Jondeau和Rockinger利用期望效用函数的Taylor展开讨论了非正态条件下的资产配置问题，发现偏度风险和峰度风险的存在对金融投资决策有显著影响[15]；Lai等基于多项式目标优化技术讨论了四阶矩的组合投资选择问题[16]。余婧用上下半方差的比值近似刻画偏度，建立了均值—方差—偏度模型，并利用该模型对中国证券市场主要股票指数进行实证分析后发现，考虑了收益率非对称性的投资组合模型较传统模型具有更优的表现[17]。宋燕玲等构建了均值—方差—偏度—正弦熵模型，并考虑了证券投资中的流动性因素，建立了带有模糊流动性约束的M-V-S-L-SE模型，结果发现，该模型比传统模型能够获得更高的累积收益率[18]。但是总体来看，采用高阶矩构造投资组合主要集中在偏度的应用上，而峰度在许多实证中发现对组合绩效的影响很小，因此本文将借鉴Rachev等使用的方法，采用在M-V模型中加入协偏度矩阵，构造M-V-S模型，以在考虑尾部风险的基础上对投资组合进行优化[19]。

相对于已有研究，本文的主要贡献在于：一方面，在传统M-V模型和最小化方差模型的基础上，分别构造了加入协偏度矩阵的M-V-S模型和CVaR最小化模型，以在优化投资组合的过程中实现对尾部风险的管理，同时利用中国股票、商品和债券等大类资产的历史数据对组合优化模型进行了实证检验，并且针对模型参数如偏度偏好系数、滚动时间窗口等进行了稳健性检验，验证了基于尾部风险的组合优化模型在构造投资组合时的有效性；另一方面，针对于夏普比率无法对投资组合风险进行有效衡量的问题，本文借鉴其他学者的研究结论，采用CVaR指标对夏普比率进行了修正，修正后的夏普比率着眼于投资组合的尾部风险，实现了对投资组合绩效更有效的刻画。

二、研究设计

(一)CVaR最小化模型

对于金融资产或投资组合来说，VaR指在特定持有期内及一定置信水平下其面临的最大可能损失，是度量尾部风险的有效指标。但是由于VaR不满足次可加性，不符合一致性风险度量的要求，因此Rockafeller和Uryasev提出了一致性风险度量指标CVaR(Conditional VaR)，弥补了VaR的不足。CVaR指在一定的置信水平β=100(1-α)%下，损失超过VaR的条件期望，公式如下：

CVaRβ(w)=E[f(w，l)|f(w，l)≥VaRβ(w)]

(1)

其中，f(w，l)为与组合投资权重w有关的损失函数，CVaR的值要大于VaR，是一个更为保守的风险测度。如果考虑收益分布，则需要计算其左尾的条件期望，则：

CVaRβ(w)=E[f(w，l)|f(w，l)≤VaRα(w)]

(2)

Rockafeller利用CVaR对均值—方差模型进行了改进，提出了均值—CVaR模型[20]：

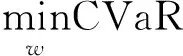
(3)

其中，w为资产权重向量，ωi为单个资产的权重。但是，由于CVaR的定义中包含了VaR，均值—CVaR的求解过程较为困难，因此可以构造辅助函数：

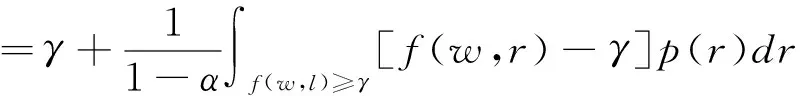
(4)

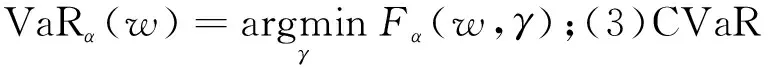
但是一般情况很难得到联合密度函数p(r)，因此可采用蒙特卡罗模拟，通过实际观测样本r1，r2，…，rT，使用经验分布函数对Fα(w，γ)近似求解：

(5)

其中，T为样本量。本文为了将CVaR最小化模型与最小化方差模型进行比较，对模型(3)不设置收益率限制条件，即不加入条件w'μ=μ0，从而计算出全局最小化CVaR投资组合。

(二)M-V-S模型

金融资产收益往往不符合正态分布，而常是左偏(负偏)或高峰的，因此仅从一阶和二阶矩(均值和方差)出发，很难对金融时间序列进行准确的认识。负偏度的存在使得资产收益下降的可能性远大于上升的可能性，从而增加了尾部风险，因此本节借鉴Rachev等的研究思路，在均值—方差模型的基础上加入对偏度的分析，从而使得模型能够实现对尾部风险的管理[13]。

设有N个风险资产，其收益向量为R=(R1，R2，…，RN)′，μ=E(R)=(E(R1)，E(R2)，…，E(RN))′为风险资产的期望收益向量，则N个资产的协偏度矩阵S可以定义为：

S=E[(R-μ)(R-μ)′⊗(R-μ)′]

(6)

其中，⊗表示克罗内克积，则投资组合收益的偏度可以由下式计算：

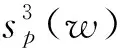
=w′S(w⊗w)

(7)

则加入偏度的均值—方差模型(M-V-S)可以表示为：

(8)

其中，δ为风险规避系数，为了保持模型结构的一致性，本文中M-V模型和M-V-S模型均取值为4；λ为偏度偏好系数，本文设定为4，在稳健性检验中将对λ的不同取值进行检验。当λ越高时，表明投资者越倾向于正偏的资产，投资组合的尾部风险将会更低。

(三)投资组合绩效评价指标

常用来衡量投资组合绩效的是夏普比率，表示单位风险下所能提供的超额收益率，计算公式为：

(9)

但是夏普比率以标准差作为投资组合风险的衡量指标，假定资产收益率符合正态分布，没有考虑资产收益率的尖峰厚尾及有偏等非正态分布特征。因此，Alexander和Baptista采用VaR指标代替标准差，对SR指标进行了修正，计算公式为：

(10)

VaR虽然能够反映高阶矩信息，从而更符合金融资产收益率尖峰厚尾及有偏的特性，从而弥补了标准差指标的缺陷，但是VaR不满足次可加性，即用VaR度量的组合风险不一定小于单个资产风险之和，从而违背风险分散化原理，不是一致性风险度量工具。因此，黄金波等采用CVaR替换夏普比率的标准差，同样构造了修正的SR指标，计算公式为：

(11)

根据CVaR的性质，SR-adj指标具有规模不变性和随机占优单调性等特性，且能保证资产组合的SR-adj值大于所有单个资产SR-adj值中的最小值，因此用SR-adj在对投资组合尾部风险进行分析时，能够更好的反映投资组合绩效。因此本文将主要采用SR-adj指标对投资组合的绩效进行评价，同时辅以SR指标进行分析。

三、实证检验

(一)变量选取及数据预处理

为了验证CVaR和M-V-S模型的有效性，本文选取了沪深300、中证500、南华工业品、南华农产品及5年期国债期货五大类资产指数作为投资组合的基准资产。其中沪深300和中证500指数分别代表大盘股票和小盘股票，南华工业品和南华农产品代表商品类资产，债券类资产选择了5年期国债期货(1)由于中国企业债与国债走势相关性极强(相关系数高达0.95以上)，为了保证分析结果能够在投资实践中具有更强的可操作性(综合性更强的债券指数很难使用高比率的杠杆)，选择国债期货作为债券类资产的代表；同时由于10年期国债期货2015年才上市，数据量比5年期国债期货要短，因此选择5年期国债期货。。沪深300指数和中证500指数于2005年1月开始编制，因此选取这些指数2005年1月至2019年2月的所有周数据进行分析。中国5年期国债期货在2013年9月6日才开始上市，因此2013年9月6日以前的数据由5年期国债指数进行补齐(2)国债期货与国债指数的相关系数在0.86以上，且笔者的前期研究证明了采用国债指数进行分析的结果是一致的，本文为了加强论文的实践可应用性，选择了国债期货作为分析对象；在对数据进行补齐时，将5年期国债指数2013年9月6日的数据调整到与国债期货相一致，之前的数据也进行等比例调整。。之所以采用周数据，是因为周数据频率适当，既可以捕捉到资本市场近期的波动，同时又可以避免频繁调仓导致交易成本过高的弊端。整个样本期间共733周，数据来自wind金融数据库。

表1报告了五类资产周收益率的描述性统计情况，其中第1列和第2列为将周收益率和周波动率进行年化后得到的数据；MDD为最大回撤，为在选定周期内任一历史时点往后推，资产净值曲线走到最低点时的收益率回撤幅度的最大值。从表中数据可以看到，中证500指数为代表的小盘股股票的年化收益率最高，但是其风险也是最大的(无论是年化波动率、MDD、VAR还是CVaR都是五类资产中最大的)，由于收益率较高，因此其夏普比率(SR)和调整后夏普比率(SR-adj)分别为0.405 3和1.164 8，均高于其他四类资产；沪深300指数的收益和风险均仅次于中证500，其夏普比率为0.344 5，但是由于其尾部风险相对国债期货高出许多，因此SR-adj为1.072 2，略低于国债期货的1.097 4；商品的风险介于股票和债券之间，工业品在样本期间的表现要明显好于农产品，其年化收益率为6.38%，而农产品的年化收益率仅为-0.5%；国债期货的风险最低，但是其收益也较低(仅高于农产品)，其SR和SR-adj分别为0.336 6和1.097 4，均处于较高水平；从偏度上看，只有国债期货的偏度为正，其他均为负值，说明国债期货的尾部风险最低。

表1 资产周收益率的描述性统计结果

构建投资组合最主要的目的是分散风险，而资产间的低相关性是分散风险的前提。表2报告了五类资产指数间的相关系数矩阵，可以看到，除了两个股票指数之间及两个商品指数之间的相关系数较高之外，其他的相关系数均较小且显著性很低，其中国债期货与其他四类资产间的相关系数均为负(其中两个显著，两个不显著)，说明通过对所选五类资产指数进行组合配置，可以有效的降低投资组合的风险。

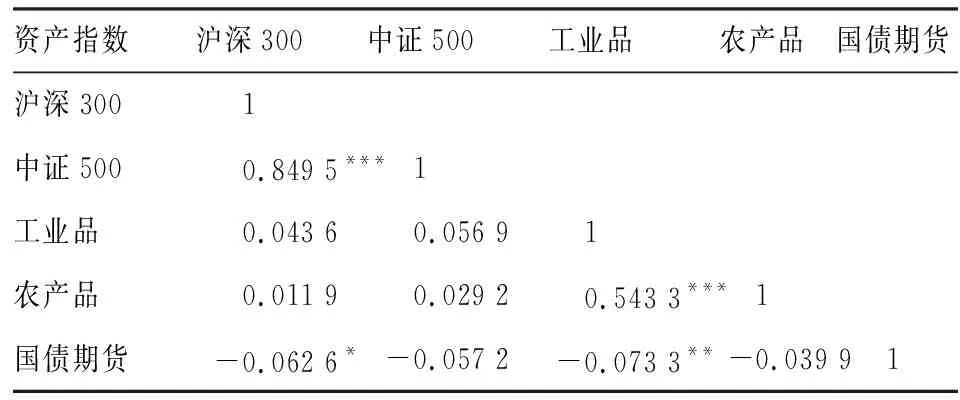
表2 资产收益率相关性系数矩阵

由于国债期货的波动率过低，如果直接采用原始数据构造投资组合，会导致国债指数所占比重过大(初步计算显示，国债期货在模型中的占比超过了90%)，从而使得研究失去意义。考虑到商品期货和国债期货均能够自由使用杠杆(商品期货的杠杆限制在20倍左右，国债期货的杠杆限制在50倍左右)，且无需融资成本，因此根据风险平价原理，对商品期货和国债期货适当增加杠杆，以使其风险与股票大体相当。计算结果显示，对工业品的杠杆应为1.6倍左右，对农产品的杠杆应为3倍左右，对国债期货的杠杆应为12倍左右(沪深300指数的波动率虽然比中证500指数低，考虑到股市中融资的限制，股票指数均采用原始数据)。表3报告了加杠杆后资产周收益率的描述性统计分析结果，可以看到，增加杠杆后，工业品和国债期货的收益率及风险调整后收益均有了大幅提高，尤其是国债期货，其年化收益率、SR和SR-adj分别提高了44.95%、1.576 9及5.169 4，远高于其他资产。加杠杆后的五类资产指数间的波动率及CVaR均比较接近，在利用组合优化模型尤其是最小方差组合及CVaR最小化组合时，所得到的资产权重能够更为合理，而不像原始数据那样，使得某类资产所占权重过高。

表3 加杠杆后资产周收益率的描述性统计结果

(二)静态投资组合

1.风险收益统计

将样本区间看成一个整体，通过组合优化模型求得各投资组合中的资产权重，并保持资产权重在整个样本区间不变。均值—方差组合(M-V)、最小化方差组合(Minrisk)、CVaR最小化组合(CVaR)及均值—方差—偏度组合(M-V-S)的风险及收益情况如表4所示。可以看到，M-V-S组合的年化收益率最高，达到了38.15%；Minrisk组合的年化波动率最低，仅为14.42%；M-V-S组合加入了组合偏度作为优化对象，因此其偏度最高，达到了0.439 5，而Minrisk和CVaR组合都是负偏的；CVaR模型的最大回撤和CVaR值均是最低，说明CVaR模型很好的控制了组合的尾部风险；从SR来看，M-V模型最高，达到了1.693，但是由于其尾部风险偏高，因此其SR-adj为5.617 1，略低于M-V-S模型的5.827 1；CVaR组合无论是SR还是SR-adj都要高于Minrisk组合。

由于Minrisk和CVaR两个模型是全局方差或全局CVaR最小化模型，并没有考虑收益，因此这两个模型的收益率均偏低，但是总体来看，CVaR模型在控制风险尤其是尾部风险方面，均要优于Minrisk，且风险调整后收益更高(无论是SR还是SR-adj)。M-V-S模型由于在原有的均值-方差模型中加入了偏度因子，因此其投资组合会有更高的上行波动率(但是更高的上行波动率并不代表风险，反而能使实际的投资组合业绩更好)，从而导致其组合波动率相对于M-V模型更高。因此，使用夏普比率来判断M-V模型和M-V-S模型组合绩效的优劣有失公允，采用调整后的夏普比率来对两个组合进行判断，可以得到更符合实际的结果。表4的结果也验证了，M-V-S模型虽然不能改善M-V的夏普比率，但是采用CVaR衡量风险的调整后夏普比率却显示M-V-S模型的效果更佳。

表4 静态投资组合的风险收益统计

图1报告了四种静态投资组合的净值曲线图，由于组合之间净值差距较大，因此采用了对数坐标轴。可以看到，M-V组合和M-V-S组合的走势接近，Minrisk组合和CVaR组合的走势接近，前两个组合的净值曲线要远高于后两个组合。整个样本区间内，M-V-S组合的净值曲线整体在M-V组合之上，而CVaR组合则只是略高于Minrisk组合。但是总体来看，无论是哪种组合，净值曲线均保持了较好的上升趋势，对风险均实现了较为有效的控制，这得益于表2所报告的五类资产指数间的低相关性。

2.资产权重分析

投资组合间的绩效差异来自于对各资产指数权重的配置差异。表5报告了四种投资组合对五类资产指数的配置权重，相对于Minrisk和CVaR组合，M-V和M-V-S组合配置了更多的中证500、国债期货，以及更少的沪深300及商品指数，由于国债期货和中证500指数的收益率最高，从而导致M-V和M-V-S组合的收益率要远高于Minrisk和CVaR组合。但是Minrisk和CVaR组合由于在各资产间的配置更为均衡，从而使得组合的风险更低。对比M-V-S组合和M-V组合，可以看到，M-V-S组合配置了更多的国债期货，由于国债期货的收益率最高，从而使得M-V-S组合年化收益率最高。而CVaR组合的资产配置与Minrisk组合较为相似，从而使得两者的净值曲线极为相似，但是由于CVaR考虑的是尾部风险，而Minrisk却是以波动率为优化对象，进而导致CVaR模型的尾部风险更低，相应的风险调整后收益更高。

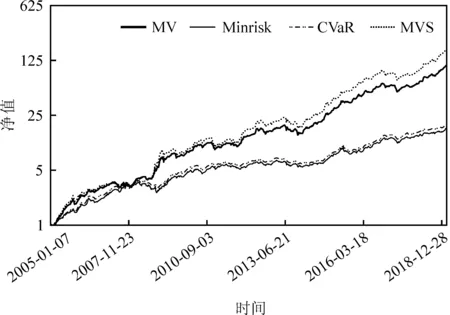
图1 静态投资组合的净值曲线图

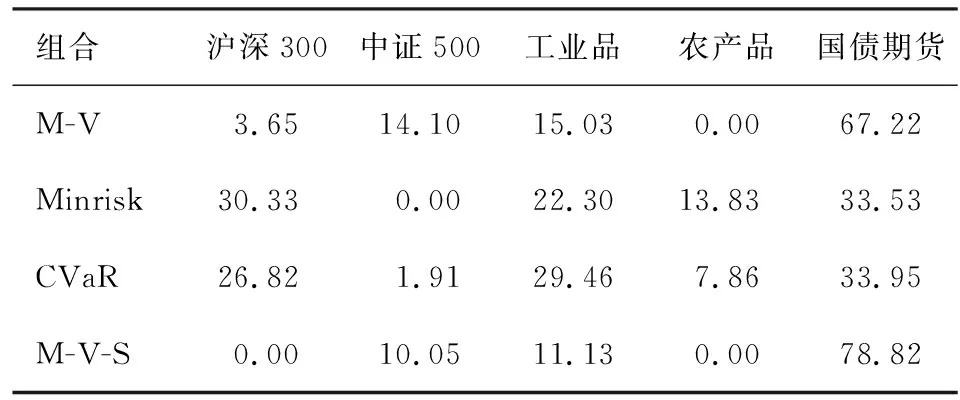
表5 静态投资组合的资产配置权重 单位：%

3.稳健性检验

由于公式(8)中组合偏度的系数λ代表投资者对偏度的偏好程度，因此当λ不同时，构造的投资组合会有差异，本节将对λ进行稳健性检验。表6报告了λ分别取值为2、4、6和8时M-V-S投资组合的风险收益统计情况，可以看到，当λ变大时，组合的年化收益率逐渐提升，但是风险也不断升高，从而导致组合的SR不断降低，但是由于尾部风险上升速度相对波动率要慢，因此SR-adj并没有明显的下降。将表6的结果与表4中的M-V组合绩效进行比较可以看到，不同λ系数下，虽然M-V-S组合的SR一直低于M-V组合，但是SR-adj始终高于M-V组合，充分说明了M-V-S模型在控制投资组合尾部风险时的有效性，而且由于λ=4时并不是M-V-S模型表现最优的参数，因此之前的研究结果是稳健的，即M-V-S模型可以对投资组合的尾部风险调整后收益进行改善。

表6 M-V-S组合的风险收益统计

(三)动态投资组合

1.风险收益统计

前述分析是建立在全样本的静态投资组合构造基础上的，可以理解为一种回溯检验，这在现实环境下是无法实现的。因此，本节采用滚动时间窗口构建投资组合，并分析和比较动态投资组合的绩效。首先，采用50周(即接近一年的时间)为窗口进行滚动，即采用t-50至t-1期的资产指数收益率序列来构造第t期的投资组合，并根据第t期资产指数的收益率来计算投资组合在第t期的收益率，并依次滚动，每周调仓，不考虑交易成本。在后面的分析中将对时间窗口进行稳健性检验。

表7报告了动态投资组合的风险及收益统计结果，可以看到与静态投资组合相似的结果，即M-V模型和M-V-S模型的收益和风险均远高于Minrsik和CVaR模型；M-V模型的SR略高于M-V-S模型，但是由于M-V-S模型更好的控制了尾部风险，因此M-V-S模型的SR-adj达到7.685 2，高于M-V模型的7.198 3；CVaR模型虽然年化波动率和最大回撤要高于Minrisk，但是其对尾部风险进行了更好的控制，表现为更低的VAR和CVaR值，且由于CVaR模型的年化收益率更高，从而导致CVaR模型的SR和SR-adj均要远高于Minrisk组合；由于CVaR动态组合对尾部风险控制的卓越表现，其SR-adj甚至超过了M-V和M-V-S组合。总体而言，动态投资组合得出的结论与静态投资组合相似，即CVaR组合和M-V-S组合通过有效的控制尾部风险，能够获得更高的调整后夏普比率，且动态组合由于能够对市场状况进行更及时的反馈。除了Minrisk组合外，其他组合的SR和SR-adj均要高于静态投资组合。图2报告的动态投资组合净值曲线可以看到，M-V组合和M-V-S组合的净值曲线走势仍然相似，只是M-V组合净值曲线一直在M-V-S组合之上；相对于静态投资组合，CVaR动态组合的净值曲线要远高于Minrisk组合，说明通过时间窗口滚动能够更好的实现尾部风险的管理。

表7 动态投资组合的风险收益统计

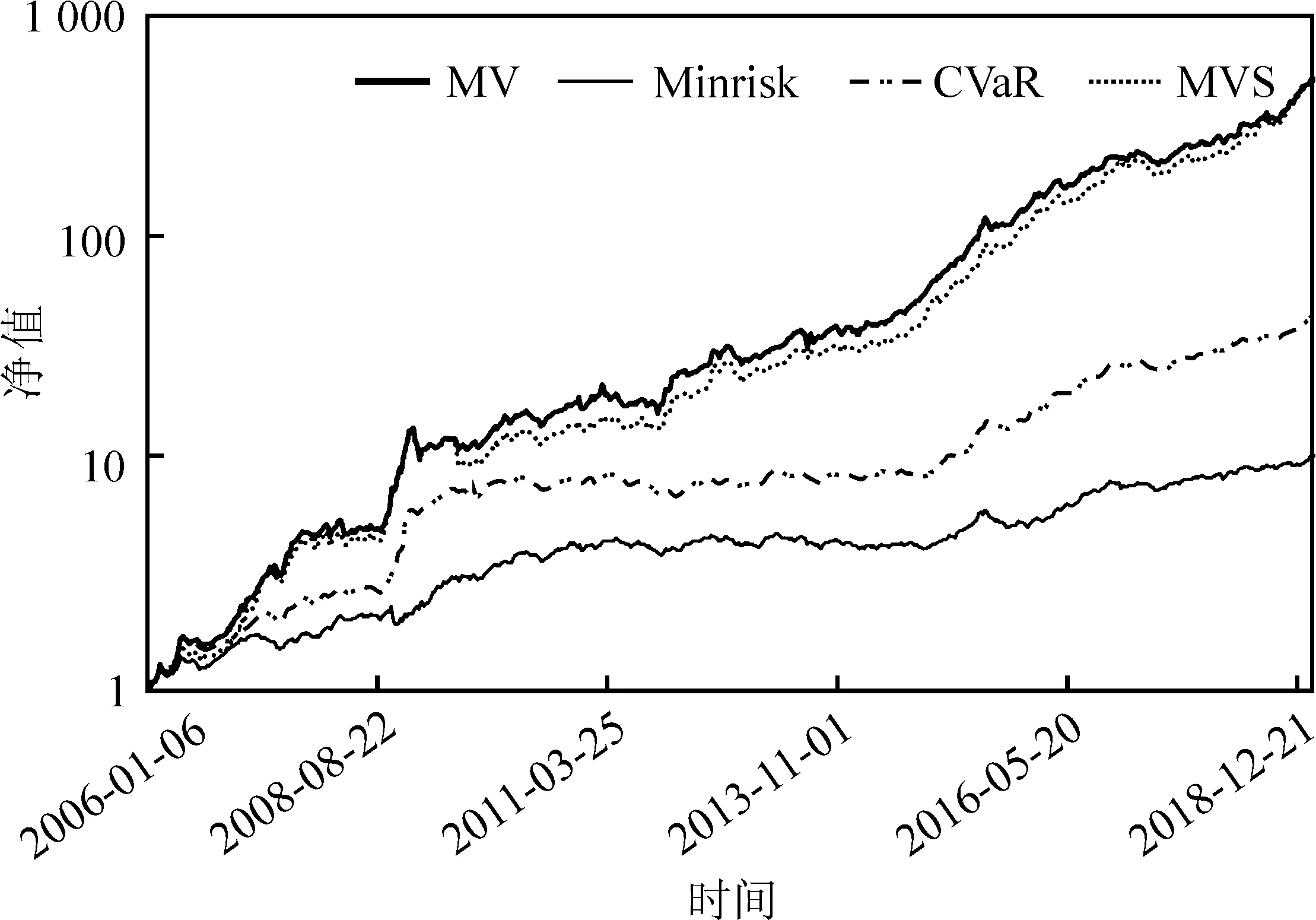
图2 动态投资组合的净值曲线图

2.资产权重分析

同样对动态投资组合的资产权重进行分析，以识别投资组合的收益差异来源。表8报告了动态投资组合在样本区间的平均资产权重，可以看到，M-V组合和M-V-S组合的资产分布明显更分散了，其国债期货的权重分别从静态投资组合的67.22%和78.82%下降到了49.08%和51.06%，同时，除了工业品的权重有所降低之外，其他三类资产的权重都有所提升；Minrisk的平均资产权重与静态投资组合相似，而CVaR组合则相对静态投资组合在资产间分配的更为均衡。因此总体来看，较高的国债期货占比是M-V和M-V-S组合收益率更高的原因所在，而在资产间更均衡的权重分配是Minrisk和CVaR组合在风险控制上表现更优的原因所在，这与静态投资组合的分析结果是一致的。

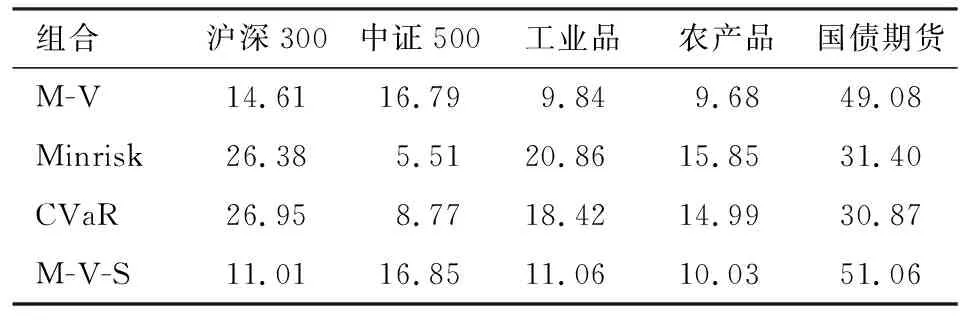
表8 动态投资组合的平均资产权重 单位：%

3.稳健性检验

对时间窗口进行稳健性检验，分别选择25周(约0.5年)、75周(约1.5年)、100周(约2年)和125周(约2.5年)的时间窗口对投资组合的绩效进行检验，结果如表9所示。可以看到，随着时间窗口的变长，所有投资组合(除125周窗口下的Minrisk组合)的绩效均表现出下降的趋势，即投资组合收益率降低，但由于风险却没有跟着下降，从而导致SR和SR-adj纷纷下降。在每个时间窗口下，M-V组合和M-V-S组合的SR和SR-adj均要高于Minrisk组合和CVaR组合(除25周的CVaR组合外)；M-V-S组合的SR要低于M-V组合(除75周外)，而SR-adj要高于M-V组合；CVaR组合无论是SR(除125周外)还是SR-adj均要高于Minrisk组合。且无论在哪个时间窗口下，M-V-S组合都取得了1左右的偏度，而Minrisk组合的偏度始终为负，M-V组合和CVaR组合虽然在个别时间窗口偏度高于M-V-S组合，但是整体来看，M-V-S在偏度控制上最为有效的。综合来看，M-V-S模型和CVaR模型有效的控制了投资组合的尾部风险，从而使得投资组合获得了更高的调整后夏普比率，研究结果在不同时间窗口下均是稳健的。

四、结论与讨论

选取2005年1月～2019年2月沪深300指数、中证500指数、南华工业品、南华农产品及5年期国债期货的周收益率数据，并根据风险平价原理对南华工业品、南华农产品和国债期货适当增加杠杆以使得各资产间的波动率大体相似，利用M-V、最小化方差(Minrisk)、最小化CVaR及M-V-S模型对五类资产分别构造静态和动态投资组合，以CVaR修正后的夏普比率(SR-adj)比较了基于尾部风险的投资组合优化方法与传统投资组合优化方法间的绩效差异，研究结果表明：考虑了尾部风险的CVaR组合和M-V-S组合均表现出了比传统组合(分别是Minrisk组合和M-V组合)更高的SR-adj，M-V组合和M-V-S组合由于在优化模型中考虑了收益的最大化，因此表现出了比CVaR组合和Minrisk组合更高的收益率及SR-adj；且该研究结论无论是采用静态投资组合还是利用滚动时间窗口构造动态投资组合均有效，在控制了偏度偏好系数及滚动时间窗口时，研究结论也是稳健的。相对于已有对投资组合的研究，本文的创新之处在于：一方面，采用CVaR和协偏度矩阵构造了基于尾部风险的投资组合优化模型，并利用中国大类资产数据对组合优化模型进行了实证检验，验证了投资组合优化模型的有效性；另一方面，采用CVaR指标对夏普比率进行了修正，修正后的夏普比率着眼于投资组合的尾部风险，能够对投资组合绩效进行更有效的刻画。

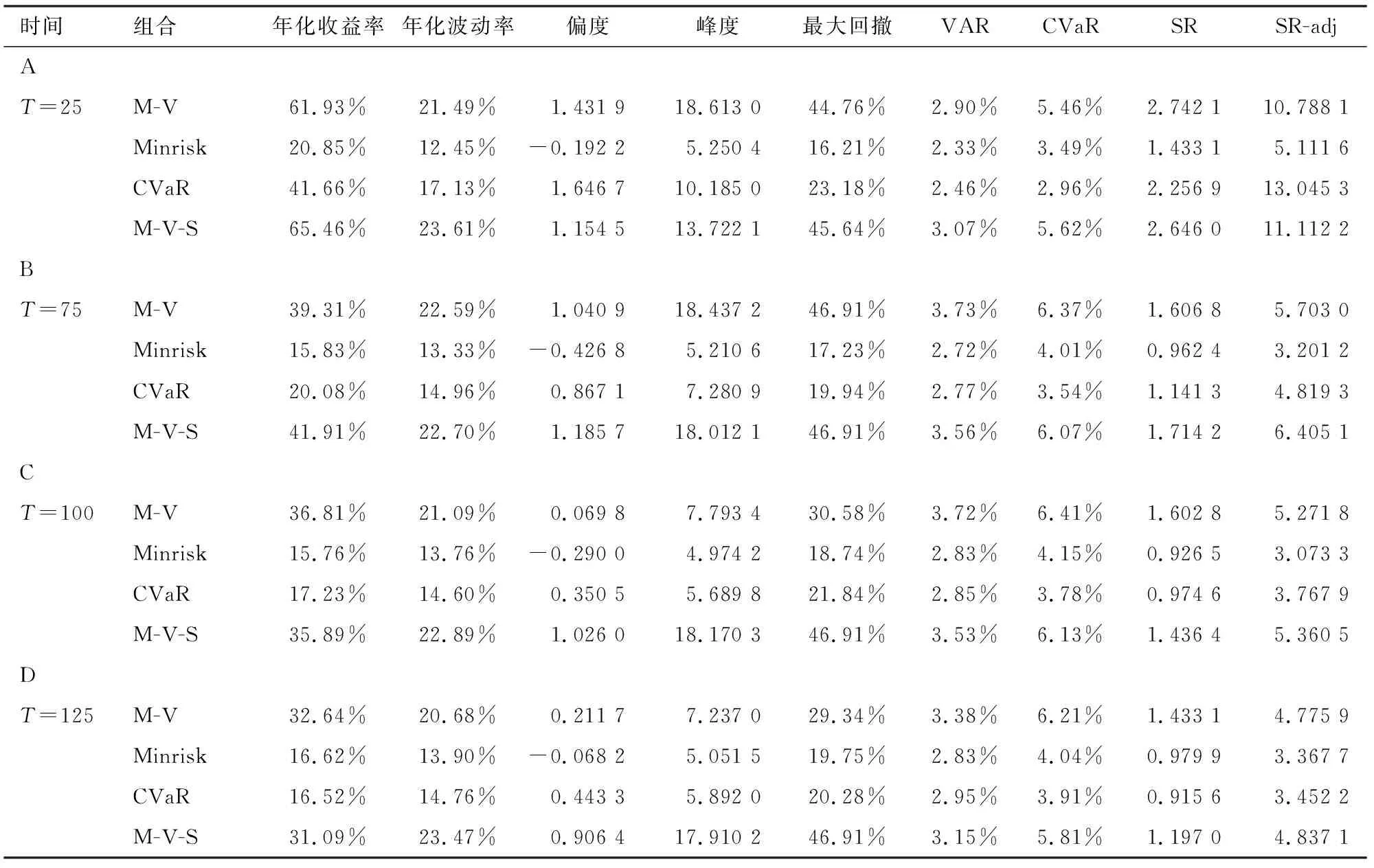
表9 基于时间窗口的稳健性检验

本文的研究结论是中国投资组合理论的有力补充，同时对于投资者来说具有一定的实践借鉴价值：第一，波动率虽然是衡量投资风险的常用指标，但并不是最有效的指标，因为当资产上行波动率增加时往往能够给投资者带来更高的投资收益，因此在构建投资组合时应重点考虑资产的下行风险，尤其是加大对尾部风险的管理，如本文采用CVaR最小化和M-V-S模型都可以在投资组合优化过程降低组合的尾部风险，从而使得投资组合的风险调整后收益有了明显改善；第二，应该采用合适的指标来对投资组合绩效进行衡量，常用的夏普比率虽然能够对风险调整后收益进行有效衡量，但是由于其对风险的度量是基于投资组合的标准差，而金融资产收益率的非正态分布状况使得用标准差来度量投资风险并不有效，如本文提出的采用CVaR作为风险指标来计算夏普比率的方法，可以对投资绩效进行更有效的度量，因此投资者在实际交易过程也应该采用多种指标对投资绩效衡量，而不仅仅是简单依赖夏普比率；第三，低相关性的资产在构造投资组合时能够有效分散投资风险，在本文的研究中，债券由于与其他资产间的相关性较低甚至为负相关，因此在投资组合中增加债券的权重可以实现风险的有效分散，甚至由于加杠杆后的债券收益率高于其他资产，债券资产权重的增加还使得投资组合的收益得到了大幅提升，因此投资者在实际投资过程中应注重资产种类的配置，通过多种资产的配置来实现对风险的分散。