仅有三个非负特征值的图

2020-06-18糟玉英王国平

华中师范大学学报（自然科学版） 2020年3期

糟玉英，王国平

(1.新疆工程学院数理学院，乌鲁木齐 830029；2.新疆师范大学数学科学学院，乌鲁木齐 830017)

本文考虑的图皆为简单无向图.设图G的点集为V(G)={v1，v2，… ，vn}.用A(G)=(aij)n×n来表示图G的邻接矩阵，其中，若vi和vj相邻则aij=1，否则aij=0.因为是实对称的，所以A(G)可以将其特征值设为λ1(G)≥λ2(G)≥…≥λn(G).A(G)的特征值也称为图G的特征值，由G的所有特征值构成的集合被称为图G的谱．

关于图的谱的研究结果有很多.文献[1]刻画了仅有一个特征值小于-1的连通图.文献[2]中确定了至多有两个非负特征值的简单图.文献[3]确定了至少有6个非零特征值的二部图.文献[4]得到了仅有两个非负特征值的图的第三大特征值.文献[5]描述了恰好有两个非负特征值的图．

设图G的边集和点集分别为E(G)和V(G).若图G是连通的且其点集和边集满足E(G)|=V(G)|-1+c，则称G为c圈图.当c=0，1，2，3时，G被分别称为树、单圈图、双圈图、三圈图.文献[6]确定了带有k个悬挂点的三圈图中谱半径最大的图.文献[7]刻画了带有完美匹配的三圈图中具有最大特征值的图.文献[8]得到了三圈图中具有最大无符号拉普拉斯谱半径的图.文献[9]刻画了第二大特征值不超过1的所有三圈图.文献[10]刻画了二部三圈图中谱半径最大的图．

本文首先确定了仅有三个非负特征值的所有树、单圈图、双圈图和三圈图，同时也确定了仅有三个非负特征值的非连通图．

1 满足λ3(G)≥0和λ4(G)<0的连通图G

设G是一个连通图，其顶点集为V(G).让V′⊆V(G)，将V′中的点按照原来在G中的邻接关系进行连接后得到的图就称为G的诱导子图．

引理1[11]设G是一个n阶连通图，H是G的m阶诱导子图.G和H的特征值分别为λ1(G)≥λ2(G)≥…≥λn(G)和λ1(H)≥λ2(H)≥…≥λn(H).那么当1≤i≤m时，λi(G)≥λi(H)≥λn-m+i(G).

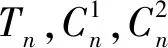
引理2[11]设G是一个二部图，则其谱是对称的，即若θ是G的m重特征值，那么-θ也是G的m重特征值．

由引理2易知下列引理3成立．

引理3若T∈T7,则T恰有四个非负特征值．

用Pn，Sn和Cn分别表示n个点的路，星图和圈.双星图Sa，b是将a和b个点分别连接在P2的两端后得到的(a+b=n-2).图H6是将一条边的端点粘在P5的中间点上后得到的．

定理1设T∈Tn.若λ3(T)≥0且λ4(T)<0，则T同构于下列图中的一个：

S4，S2，1，P5，P6，H6.

证明明显地，n≥4.当n≥7时，容易观察到对于Tn中的任一个树T都含有七个点的子树T7作为其诱导子图.根据引理1及引理3可知，λ4(T)≥λ4(T7)，这表明，T同样至少有四个非负特征值.因此，可以认为4≤n≤6．

借助Maple计算后容易看出，当λ3(T)≥0且λ4(T)<0时，T同构于下面五个图中的一个：S4，S2，1，P5，P6，H6．

用Cn+v表示将一个点与Cn的某个点连接后得到的图；用C3⊙2表示将两个点与C3的同一个点连接后得到的图；用Cn⊕2v表示将两个点分别与Cn的两个相邻点连接后得到的图；用C3+Pn表示将Pn的一个端点与C3的某个点连接后得到的图；用C3⊙2P2表示将两条P2各自的一个端点与C3的同一个点连接后得到的图；用C3⊕2P2表示将两条P2各自的一个端点分别与C3的两个相邻点连接后得到的图；用C3⊙v⊙P2表示将一个点及P2的一个端点与C3的同一个点连接后得到的图；用C3⊕v⊕P2表示将一个点及P2的一个端点分别与C3的两个相邻点连接后得到的图；用C3⊕3v表示将三个点分别与C3的三个点连接后得到的图；用C3+P3表示将P3的中间点与C3的某个点连接后得到的图；用C3+P4表示将P4的某个二度点与C3的某个点连接后得到的图．

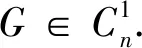
Ck(4≤k≤7)，C4+v，C5+v，C3⊙2v，

C3⊕2v，C4⊕2v，C3+P3，C3+P4，

C3⊙2P2，C3⊕2P2，C3⊙v⊙P2，

C3⊕v⊕P2，C3⊕3v，C3+P3，C3+P4.

证明当n≥8时，可观察出G至少含有七个点的树T7作为其诱导子图.由引理1及引理3可知，λ4(G)≥λ4(T7)，这表明G至少有四个非负特征值.明显地，n≥4，故可确定4≤n≤7．

借助Maple计算得到，当λ3(T)≥0且λ4(T)<0时，G同构于下列十八个图中的一个：

Ck(4≤k≤7)，C4+v，C5+v，C3⊙2v，

C3⊕2v，C4⊕2v，C3+P3，C3+P4，C3⊙2P2，C3⊕2P2，C3⊙v⊙P2，

C3⊕v⊕P2，C3⊕3v，C3+P3，C3+P4.

哑铃图是将两个点不交的圈分别粘在一条路的两个端点后得到的；∞图是由恰有一个公共点的两个圈构成的；θ图是将不同的两个点用三条内部不交的路连接起来后得到的，其中三条路中至多有一条路的长度为1.显然，任一个双圈图都是将一些树粘在哑铃图，∞图或θ图上得到的.让bn，θn及∞n分别表示带有n个点的哑铃图，∞图及θ图．

用b6+v和b6+P2分别表示将一个点和P2的一个端点与b6的某个二度点连接后得到的图；用b6⊕v和b6⊕P2分别表示将一个点和P2的一个端点与b6的一个三度点连接后得到的图.用∞5+v和∞5+P2分别表示将一个点和P2的一个端点与∞5的某个二度点连接后得到的图；用∞5*v和∞5*P2分别表示将一个点和P2的一个端点与∞5的四度点连接后得到的图；用∞5+2v表示将两个点分别与∞5的两个相邻二度点连接后得到的图.用θ4⊙2v，θ4∘2v及θ4•2v分别表示将两个点与θ4中的一个二度点，不同的二度点及相邻的两个点连接后得到的图；用θ4⊙v⊙P2，θ4∘v∘P2及θ4•v•P2，分别表示将一个点及P2的一个端点与θ4的一个二度点，不同的二度点及相邻的两个点连接后得到的图；用θ4+P2和θ4+P3分别表示将P2和P3的一个端点与θ4的一个二度点连接后得到的图；用θ4⊕v和θ4⊕P2分别表示将一个点和P2的一个端点与θ4的一个三度点连接后得到的图．

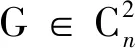
b6+v，b6+P2，b6⊕v，b6⊕P2，∞5+v，

∞5+P2，∞5*v，∞5*P2，∞5+2v，∞6，

θ4⊙2v，θ4∘2v，θ4·2v，θ4⊙v⊙P2，

θ4∘v∘P2，θ4·v·P2，θ4+P2，

θ4+P3，θ4⊕v，θ4⊕P2，Di(1≤i≤12).

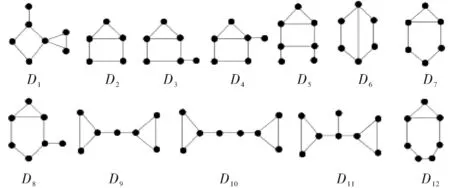
图1 Di(1≤i≤12)Fig.1 Di(1≤i≤12)

证明利用Maple可计算出λ3(θ4)=-1<0且λ4(θ4)=-1.5616<0.这意味着n≥5.当n≥9时，可观察到G至少含有七个点的树T7作为其诱导子图.根据引理1及引理3可知λ4(G)≥λ4(T7)，这说明G至少有四个特征值是非负的．

由上所述，可以确定5≤n≤8．

经过Maple计算后可以确定，G同构于下列32个图中的一个：

b6+v，b6+P2，b6⊕v，b6⊕P2，∞5+v，

∞5+P2，∞5*v，∞5*P2，∞5+2v，

∞6，θ4⊙2v，θ4∘2v，θ4·2v，θ4⊙v⊙P2，

θ4∘v∘P2，θ4·v·P2，θ4+P2，θ4+P3，

θ4⊕v，θ4⊕P2，Di(1≤i≤12).

用I1⊙2v表示将两个点与I1⊕P3I1的同一个点连接后得到的图；用I1•2v表示将两个点分别与I1的两个相邻点连接后得到的图；用和I1⊕P4分别表示将P3和P4的一个端点与I1的某个点连接后得到的图；用I1⊙v⊙P2表示将一个点及P2的一个端点与I1的同一个点连接后得到的图；用I1•v•P2表示将一个点和P2的一个端点分别与I1的两个相邻点连接后得到的图；用I1⊙2P2表示将两条P2各自的一个端点与I1的同一个点连接后得到的图；用I1+P3表示将P3的中间点与I1的某个点连接后得到的图；用I1+P4表示将P4的某个二度点与I1的某个点连接后得到的图．

用I2+v，I2⊕v及I2*v分别表示将一个点与I2的二度点，三度点及四度点连接后得到的图；用I2+P2，I2⊕P2及I2*P2分别表示将P2的一个端点与I2的二度点，三度点及四度点连接后得到的图；用I2∘2v表示将两个点分别与I2的不同二度点连接后得到的图；用I2•2v表示将两个点分别与I2的相邻的二度点和三度点连接后得到的图．

用I3+v和I3⊕v分别表示将一个点与I3的二度点和与二度点相邻的三度点连接后得到的图；用I3•2v表示将两个点分别与I3的相邻的二度点和三度点连接后得到的图；用I4+v表示将一个点与I4的某个二度点连接后得到的图；用I4∘2v表示将两个点分别与I4的不同二度点连接后得到的图；用I5+v和I5⊕v分别表示将一个点与I5的二度点和与二度点相邻的三度点连接后得到的图．

用I7⊕v表示将一个点与I7的某个三度点连接后得到的图；用I8+v表示将一个点与I8中四度点和二度点相邻的二度点连接后得到的图；用I8⊕v表示将一个点与I8中三度点和二度点相邻的三度点连接后得到的图；用I9+v表示将一个点与I9中两个三度点相邻的二度点连接后得到的图．

用I29v表示将一个点与I29中四度点相邻的二度点连接后得到的图；用I30+v表示将一个点与I30中两个三度点相邻的二度点连接后得到的图；用I30⊕v表示将一个点与I30中二度点不相邻的三度点连接后得到的图；用I31+v表示将一个点与I31中三度点相邻的二度点连接后得到的图．

用I32⊕v和I32*v分别表示将一个点与I32的三度点和四度点连接后得到的图；用I32⊕P2和I32*P2分别表示将P2的一个端点与I32的三度点和四度点连接后得到的图；用I32+v和I32+P2分别表示将一个点和P2的一个端点与I32中三度点相邻的二度点连接后得到的图；用I32v和I32P2分别表示将一个点和P2的一个端点与I32中四度点相邻的二度点连接后得到的图．

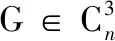
Ii(3≤i≤31)，I1⊙2v，I1·2v，I1⊕P3，

I1⊕P4，I1⊙v⊙P2，I1·v·P2，I1⊙2P2，I1+P3，
I1+P4，I2+v，I2⊕v，I2*v，I2+P2，

I2⊕P2，I2*P2，I2∘2v，I2·2v，I3+v，I3⊕v，
I3·2v，I4+v，I4∘2v，I5+v，I5⊕v，I7⊕v，

I8+v，I8⊕v，I9+v，I29v，I30+v，I30⊕v，
I31+v，I32⊕v，I32*v，I32⊕P2，I32*P2，

I32+v，I32+P2，I32v，I32P2.

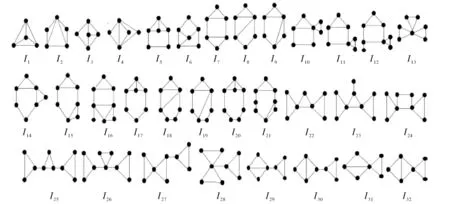
图2 Ii(1≤i≤32)Fig.2 Ii(1≤i≤32)

证明若n=4则G≅I1.利用Maple计算得出λ2(I1)=λ3(I1)=λ4(I1)=-1<0，这意味着n≥5.当n≥10时，可以观察到G至少含有七个点的树T7作为其诱导子图.根据引理1及引理3得到λ4(G)≥λ4(T7).显然可知，G的特征值至少有四个是非负的.因此得出5≤n≤9.经过Maple计算后得出，当λ3(T)≥0且λ4(T)<0时，G同构于下列六十九个图中的一个：

Ii(3≤i≤31)，I1⊙2v，I1·2v，I1⊕P3，

I1⊕P4，I1⊙v⊙P2，I1·v·P2，I1⊙2P2，I1+P3，
I1+P4，I2+v，I2⊕v，I2*v，I2+P2，

I2⊕P2，I2*P2，I2∘2v，I2·2v，I3+v，I3⊕v，
I3·2v，I4+v，I4∘2v，I5+v，I5⊕v，I7⊕v，

I8+v，I8⊕v，I9+v，I29v，I30+v，I30⊕v，
I31+v，I32⊕v，I32*v，I32⊕P2，I32*P2，

I32+v，I32+P2，I32v，I32P2.

定理5设G是一个k(k≥4)圈图.若λ3(T)≥0且λ4(T)<0，则5≤n≤6+k．

证明由k≥4很容易看到，n≥5.假设n≥k+7.接下来，通过去点破除G中的圈.由于G是k圈图，所以至多删掉G中的k个点可以破圈.这样，得到的G的诱导子图就是一个至少含有七个点的树T7.根据引理1及引理3，得出λ4(G)≥λ4(T7).这说明G的特征值至少有四个是非负的，这与G仅有三个非负特征值矛盾．

由上所述，可以确定5≤n≤6+k．

2 满足λ3(G)≥0和λ4(G)<0的非连通图G

参照文献[4]，首先给出Gm的定义．

用NG(v)表示图G中点v的邻点集，再记NG[v]=NG(v)∪{v}.设G1和G2是两个不交的完全图，其点集分别为V(G1)={v1，v2，…，v「m/2⎤}和V(G2)={w1，w2，…，w⎣m/2」}.Gm(m≥2)是按照下面的要求在G1和G2之间添加一些边之后得到的：

2) |NGm[vi]∩V(G2)|=i-1，这里的i=1，…，「m/2⎤；

3) 当m为偶数时，有|NGm[wj]∩V(G1)|=j-1；当m为奇数时，有|NGm[wj]∩V(G1)|=j，这里j=1，…，⎣m/2」．

下面的图3给出了当2≤m≤ 6时Gm的图结构．

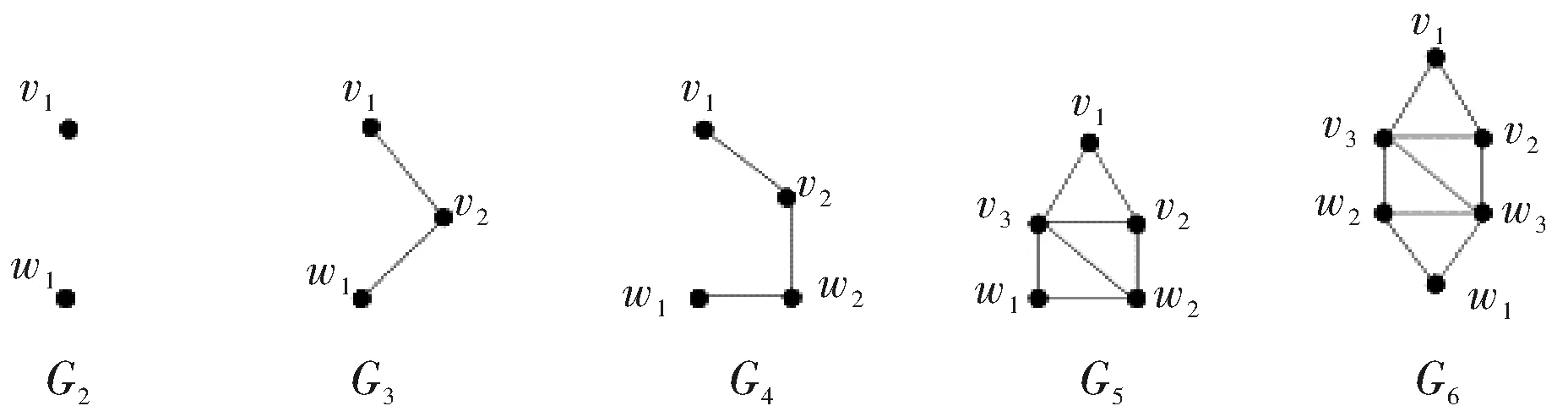
图3 Gm(2≤m≤6)Fig.3 Gm(2≤m≤6)

设Kn是n个点的完全图.将Gm中的m个点v1，v2，…，vm分别用Kn1，Kn2，…，Knm去替换，并且如果vi和vj在Gm中是相邻的且1≤i≠j≤m，那么就将Kni中的每个点和Knj中的每个点相连；否则，就不连.这样得到的图记为Gm[n1，n2，…，nm].

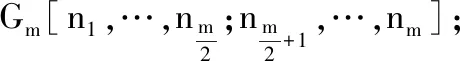
若图X和图Y是同构的，那么记为X≅Y；否则，记为XY．

引理4[5]设图G是一个带有n(n≥3)个点的连通图，那么

1) 若λ2(G)>0且λ3(G)<0，则G≅Gm[n1，n2，…，nm]，其中3≤m≤12，且Gm[n1，n2，…，nm]G3[1;1;n-2]；

2) 若λ2(G)=0且λ3(G)<0，则G≅Kne．

所有患者术后72 h行颅脑增强MRI检查肿瘤切除情况，根据Simpson分级标准，达到Ⅰ级 58例，Ⅱ级13例，Ⅲ级9例。术后送病理检查均诊断为脑膜瘤，Ⅰ级良性脑膜瘤59例，Ⅱ级非典型性脑膜瘤21例。术后即时发现，8例多饮多尿者中6例症状缓解，2例无明显改善；5例并发一过性尿崩；4例嗅觉减退；4例颅内感染；1例脑脊液漏；1例出现高热、血糖升高等严重下丘脑反应而死亡；1例大量出血形成脑疝而死亡。随访2～7.5年，平均(5.4±1.4)年，56例视力不同程度的改善，21例无明显变化，3例视力减退。11例复发，复发率为13.8%，再次行手术治疗。

图G的邻接矩阵A(G)的特征多项式P(G，λ)=det(λI-A(G))也称为图G的特征多项式，这里的I表示n阶单位矩阵．

引理5[5]设图Gm(m≥ 2)的邻接矩阵是A=(aij).其中n1，…，nm是正整数，令bii=ni-1(1≤i≤m)及bij=aijnj(1≤i≠j≤m)，设B=(bij)是m阶矩阵.则P(Gm[n1，n2，…，nm]，λ)=(λ+1)n1+…+nm-mf(λ)，其中f(λ)=det(λI-B).并且-1是Gm[n1，n2，…，nm]的n1+…+nm-m重特征值．

引理6[5]设G是一个n≥ 2阶连通图.则λ1(G)>0且λ2(G)<0当且仅当G≅Kn．

若G=B1∪B2∪…∪Bm，这里的m≥2,而B1，B2，…，Bm是m个没有公共点且互不相连的连通图，则称G是非连通图，B1，B2，…，Bm是G的m个连通分支．

定理6设G是一个n≥4阶非连通图.则有

1)λ3(G)>0且λ4(G)<0当且仅当G同构于下面中的一个：

Gm[n1，n2，…，nm]∪Kc，Ka∪Kc∪Kn-a-c，

其中，3≤m≤12，Gm[n1，n2，…，nm]G3[1;1;a]且a，c≥2．

2)λ3(G)=0且λ4(G)<0当且仅当G同构于下面中的一个：

Gm[n1，n2，…，nm]∪K1，Kqe∪Kn-q，

K1∪Kc∪Kn-1-c，K1∪K1∪Kn-2，

其中，3≤m≤12，Gm[n1，n2，…，nm]G3[1;1;n-3]且q≥ 3，c≥ 2．

证明假设G有m个连通分支B1，B2，…，Bm，即G=B1∪B2∪…∪Bm，其中m≥2.由Perron定理可知，λ1(Bi)≥0(1≤i≤m).因为λ4(G)<0，所以确定m≤3.由引理1及引理3容易看到，1)和2)都是成立的．

推论1如果G≅G3[a;b;c]∪Kp，那么λ4(G)=-1．