定子电流建模的差分进化与最小二乘混合算法

彭 程，郭春雨

(华北科技学院，北京 东燕郊 065201)

0 引言

断条是异步电机的一类常见故障，定子电流中周期信号的幅值能够揭示是否存在断条故障以及故障的程度，因此定子电流分析法成为断条故障诊断的一种重要方法。定子电流信号频率和幅值分析的常用算法有矩阵束算法[1]、Prony算法[2]、谱估计[3]、小波包算法[4]、自适应滤波[5]、神经网络[6]、智能优化算法[7]等。本文提出了一种用于断条故障诊断的定子电流建模算法，并使用仿真算例对算法进行了检验。

1 问题描述

已有研究表明，出现断条故障时，异步电机定子电流为：

(1)

式中，f为工频，Hz；t为时间，s；S为转差率；B1、B2、B3为各频率成分的幅值，A；φ1、φ2、φ3为各频率成分的初相角，rad。即定子电流中会出现 (1±2S)f的频率成分，并且断条数目可以按式(2)进行判断[2]。

(2)

式中，p为电机极对数；R为转子导条总数；Rb为断裂的导条数。设N+1个不同时刻定子电流的测量值为

Im(nT)=I(nT)+e(nT)

(3)

式中，T为采样周期，s；n为采样点数，n= 0, 1, 2, ...,N；e(nT)为测量噪声，服从数学期望为0、标准差为σ的高斯分布，A。定子电流建模需要解决的问题是根据Im(nT)估计出式(1)中各未知参数，尤其是f、S、B1和B3的值，以便进行断条故障诊断。本文通过求解式(4)定义的非线性最小二乘问题得到各未知参数。

(4)

式中，J为目标函数，A2。

2 差分进化算法

差分进化[8-10]是一种基于种群的智能优化算法，种群中每个个体对应于优化问题的一个可能的解。差分进化算法使用变异、交叉、选择三种操作逐步更新种群中的个体，得到优化问题的解。

对于一个D维优化问题，设种群大小为P，与种群中的第k(k=1, 2, ...,P)个个体XkRD对应的变异操作为

Vk=Xr1+F(Xr2-Xr3)

(5)

式中，Vk为变异向量；r1、r2、r3为集合{1, 2, ...,P}中三个不同的元素，且均不等于k；F为缩放因子。

交叉操作中，试验向量Uk的一部分分量来自于个体Xk，其余分量则从变异向量Vk中获取，即试验向量Uk的第i(i=1, 2, ...,D)维分量

(6)

式中，r4为[0, 1]区间内服从均匀分布的随机数；C为交叉概率，C为Vk的第i维分量；为Xk的第i维分量。

选择操作采用贪婪策略，将Uk与Xk中更优的一个作为下一代种群的第k个个体。

3 定子电流建模算法

观察式(1)给出的定子电流模型，可以知道模型的8个参数中f、S、φ1、φ2、φ3为非线性参数，B1、B2、B3为线性参数。令θ1=[B1B2B3]T，θ2=[fSφ1φ2φ3]T，若θ2已知，式(4)简化为线性最小二乘问题，并且θ1为式(7)定义的线性代数方程组的最小二乘解。

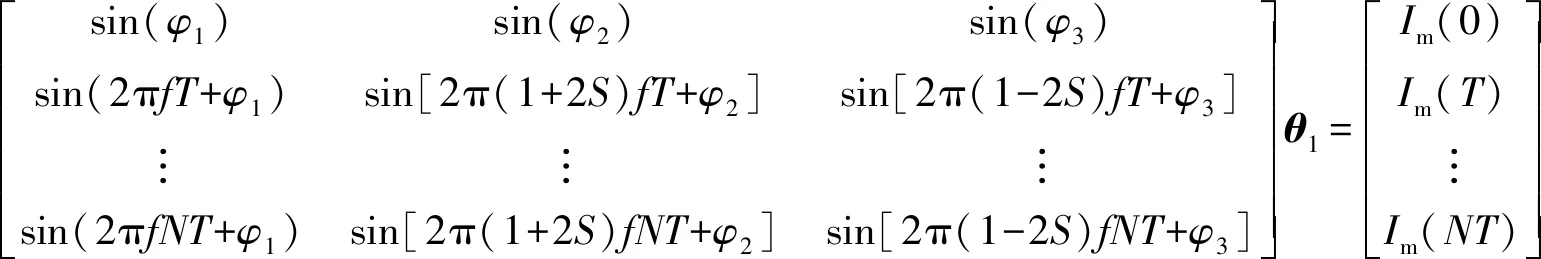
(7)

考虑到定子电流模型的这一特点，定子电流建模时对8个未知参数进行了分组，使用差分进化算法确定θ2，通过求解式(7)得到与θ2对应的θ1。本文将该定子电流建模算法称为差分进化与最小二乘混合算法。

注意到θ1的三个分量B1、B2、B3均应为非负数，而式(7)的最小二乘解不一定能满足这一约束条件，故需要对其进行修正。这里将修正步骤作为定子电流建模的最后一步，具体做法是若某频率成分的幅值的计算结果小于零，则取其绝对值作为幅值，初相角则增加π。例如优化得到的某频率成分正弦信号为-0.2sin(49t+π/3)，则将其修正为0.2sin(49t+4π/3)。

综上所述，定子电流建模的差分进化与最小二乘混合算法的流程为：

步骤1：设置差分进化算法参数，包括种群大小P、缩放因子F、交叉概率C以及最大进化代数G。设置各未知参数的取值范围。

步骤2：按随机方式生成初始种群，对初始种群的每个个体，根据式(7)计算其对应的线性参数θ1，使用式(4)计算该个体对应的目标函数值。令进化代数g=0。

步骤3：令g=g+1。依次使用变异、交叉、选择操作更新种群中每个个体。

步骤4：若g≤G，返回步骤3。否则输出种群中最优个体及其对应的θ1，作为优化问题的最优解。

步骤5：对幅值计算结果小于零的频率成分进行幅值和初相角修正，得到定子电流模型参数。

4 仿真实验

仿真中假设定子电流各参数的理论值：f=49.9 Hz，S=0.03，B1=8.00 A，B2=0.12 A，B3=0.10 A，φ1=1 rad，φ2=2 rad，φ3=5 rad；采样频率为1000 Hz，数据长度为1001；差分进化算法参数：P=100，F=0.5，C=0.9，G=200；根据定子电流各参数的特点，确定其取值范围：f[47, 53] Hz，S[0.01, 0.06]，φ1、φ2、φ3[-π/2, π/2] rad。

不考虑测量噪声的情况下，目标函数J随进化代数g的变化过程见图1。由图1可知J快速趋向于零，算法结束时最优解对应的J=5.436510-14，各参数的估计值：f=49.9000 Hz，S=0.0300，φ1=1.0000 rad，φ2=2.0000 rad，φ3=-1.2832 rad，B1=8.0000 A，B2=0.1200 A，B3=0.1000 A。除φ3外，其余参数的估计值均与理论值相同，由于φ3的估计值与理论值之间相差2π，可以知道采用上述估计值作为定子电流模型参数，能够正确表示无噪声情况下的定子电流。

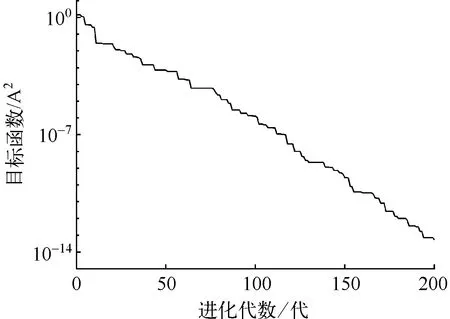
图1 目标函数变化曲线

作为对比，与不考虑定子电流模型参数特点的实验进行比较。在使用差分进化算法直接估计全部8个参数时，设B1[0, 10] A，B2、B3[0, 1] A，φ1、φ2、φ3[0, 2π] rad，其他参数的取值范围以及差分进化算法参数保持不变。

两种思路下各自进行100次仿真实验，参数估计值及J的统计结果见表1。由表1中数据可知，与直接使用差分进化算法估计全部参数相比，使用差分进化与最小二乘混合算法进行定子电流建模可以得到更高精度的解。

在e(nT)的标准差σ取0.05 A和0.10 A两种噪声水平下，使用差分进化与最小二乘混合算法各进行100次仿真实验，参数估计值和J的统计结果见表2。由表2可知，噪声情况下，该算法仍然有很强的稳定性，能够为判别断条故障的发生情况和程度提供有效依据。

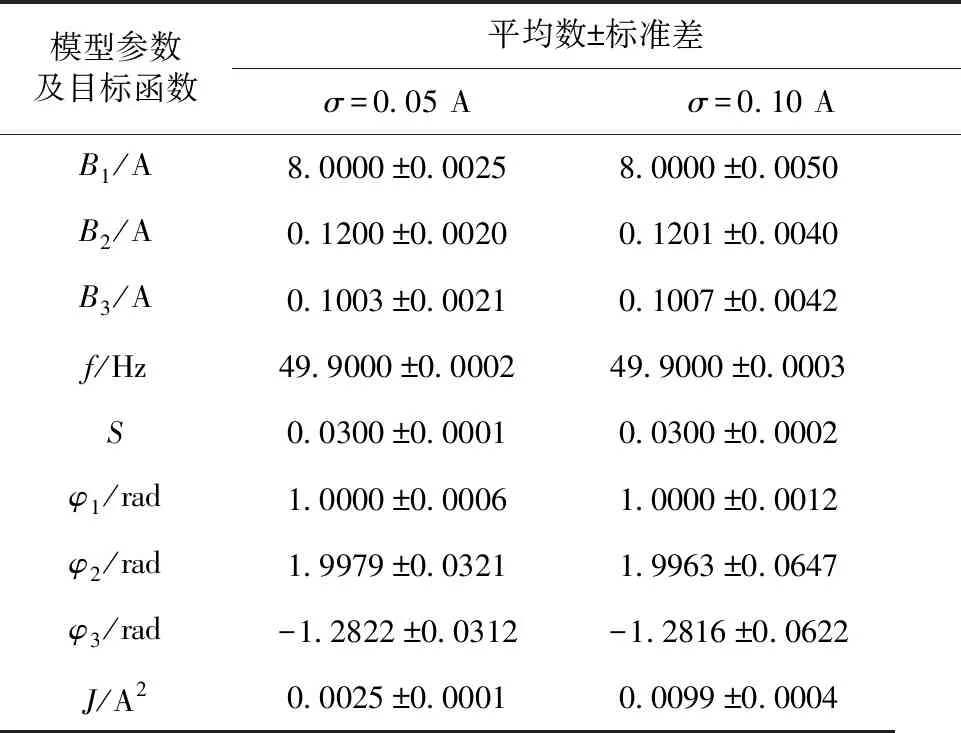
表2 不同噪声水平下仿真实验的统计结果

5 结论

(1) 使用差分进化算法，从非线性优化的角度进行定子电流建模，需要估计工频等8个参数。本文考虑到定子电流模型的结构性，使用差分进化算法估计定子电流模型中的5个非线性参数，其余3个线性参数则通过线性最小二乘算法得到。差分进化算法属于随机优化算法，而线性最小二乘是确定性算法。将差分进化算法与线性最小二乘技术相结合进行定子电流建模，它降低了差分进化算法搜索空间的维数，同时还减少了差分进化算法搜索过程中的盲目性。

(2) 不考虑测量噪声的情况下，与直接使用差分进化算法进行定子电流建模相比，差分进化与最小二乘混合算法得到了更高精度的解；存在测量噪声的情况下，差分进化与最小二乘混合算法也能够得到高精度的解，并且性能稳定，可以用于异步电机断条故障诊断。