含杂质盐岩典型蠕变模型的参数识别与对比分析

2020-06-18易海洋路乐乐武志德

华北科技学院学报 2020年2期

易海洋，路乐乐，曹伟，武志德

(1.华北科技学院，北京东燕郊 065201；2.中国矿业大学(北京)，北京 100083；3. 中国石油勘探开发研究院廊坊分院，河北廊坊 065007)

0 引言

蠕变行为是盐岩重要的力学特性，也是影响盐岩储库长期运营、稳定性、安全性的关键因素。深部地层中的盐岩储库，由于有效容积的减少和发生大变形将造成储库失效[1，2]。因此，盐岩蠕变行为的研究将对减少有效容积的损失和防止储库失效有重要的意义。

目前，国内外学者主要通过蠕变试验、理论分析、数值模拟等方式对盐岩蠕变进行了大量研究，且在理论模型方面成果显著。岩石蠕变具有复杂的非线性行为[3，4]，目前，理论模型种类繁多，可分为经验模型[4，5]、元件模型[7，8]、损伤流变模型[10]和分数阶流变模型[11，12]等。近年来，不同学者采用新的理论发展了盐岩蠕变模型，如Hou等[13]基于流变模型建立了流变损伤模型；Zhou等[14]基于分数阶微积分理论，在经典西原模型基础上，提出了基于时间的分数阶导数的盐岩蠕变本构模型；Yang等[15]也建立了能够反映盐岩的蠕变全过程的本构模型。我国盐矿多为含大量杂质和夹层的层状盐岩，而目前对盐岩蠕变模型研究多集中在纯盐岩方面，郑雅丽等[16]通过对纯盐岩和含杂质盐岩进行力学试验对比分析，发现纯盐岩与含杂质盐岩的变形能力以及力学特性明显不同，盐岩内部杂质成分将会抑制盐岩的变形能力、提高盐岩的抗压强度。由于含杂质盐岩在蠕变过程中复杂的力学特性，以及现有的蠕变模型中参数较多，使得拟合结果不具有唯一性，不能够充分揭示含杂质盐岩的蠕变特性。因此，确定参数少、模拟效果好的含杂质盐岩蠕变模型将是研究盐岩蠕变重要的方向。

本文基于含杂质盐岩分级加载蠕变试验，采用Origin拟合蠕变试验数据得到盐岩蠕变模型参数。将参数代入计算另一组成分相近、杂质随机分布的盐岩蠕变数据，对比分析各个模型在描述蠕变模型的适用性。

1 含杂质岩盐蠕变试验

1.1 试验准备及其加载方案

本次含杂质盐岩分级加载蠕变试验在室温条件下进行，使用中国石油勘探开发研究院廊坊分院地下储库工程实验室盐穴储库长期运行蠕变试验机CK/Y2014-01进行，如图1所示。试验所用的盐岩试样取自江苏金坛，采用钻孔取芯。岩芯主要含泥岩和钙芒硝杂质，NaCl含量为79%。由于盐岩易溶于水，而且在潮湿的空气中容易被潮解，则采用干式锯磨将样品加工成直径约100 mm，高约为200 mm的圆柱形试件，试验对两个样品进行了测试，实际样品尺寸、密度和加载压力见表1。

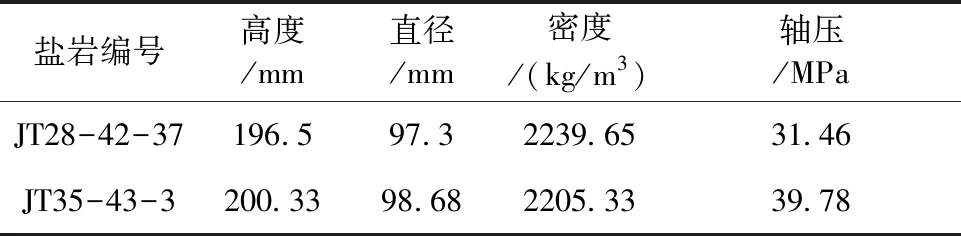
表1 盐岩样品的基本参数

1.2 试验结果

试验过程中，蠕变变形数据由试验系统自动监测，两个试验样品的蠕变应变随时间的变化曲线如图2所示，可见，两个样品经历了典型的初始蠕变和稳态蠕变阶段。但是两个样品的蠕变曲线由于杂质分布情况不同和加载应力不同，应变演化曲线在稳态蠕变增量上略有不同。总体上，两个样品的蠕变应变曲线在演化趋势上相近。

图1 试验加载示意图

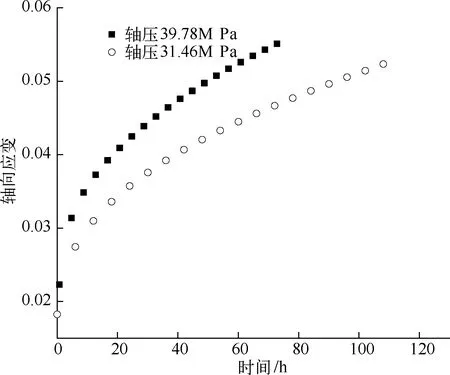
图2 蠕变试验曲线

2 典型蠕变模型参数识别

2.1 Bailey-Norton模型参数

Bailey-Norton蠕变模型为时间硬化蠕变模型之一，通过与大量的试验数据对比发现，该模型能较好的描述岩石蠕变的初始阶段和稳态阶段，并以蠕变应变率的形式进行表示：

(1)

假定岩石在蠕变过程中，温度为保持不变，即T=C，则有：

(2)

对上式两端进行积分，可以得到：

(3)

总应变ε表示为：

ε=εe+εcr

(4)

其中εe=σ/E1，E1为岩石的弹性模量，总应变ε可以表示为：

(5)

2.2 伯格斯(Burgers)模型参数

伯格斯(Burgers)模型能够较好地反映岩石在蠕变过程中发生的瞬时弹性变形、黏弹性变形以及黏性流动变形。伯格斯(Burgers)模型是典型地元件模型是由Maxwell和Kelvin体串联形成，如图3所示。

图3 伯格斯(Burgers)模型

伯格斯(Burgers)模型由弹簧、黏壶进行串并联形成，由上图可以得到总应变ε为：

ε=ε1(t)+ε2(t)

(6)

式中，ε为总应变；ε1(t)为Kelvin体表示的应变量；ε2(t)为Maxwell体表示的应变量。

总应变ε可以表示为：

(7)

式中，η1、η2分别表示岩石的黏性系数。

2.3 西原模型参数

西原模型常用来建立盐岩蠕变的本构方程，是典型的元件模型，其结构由胡克体、Kelvin体、Bingham体串联形成如图4所示。

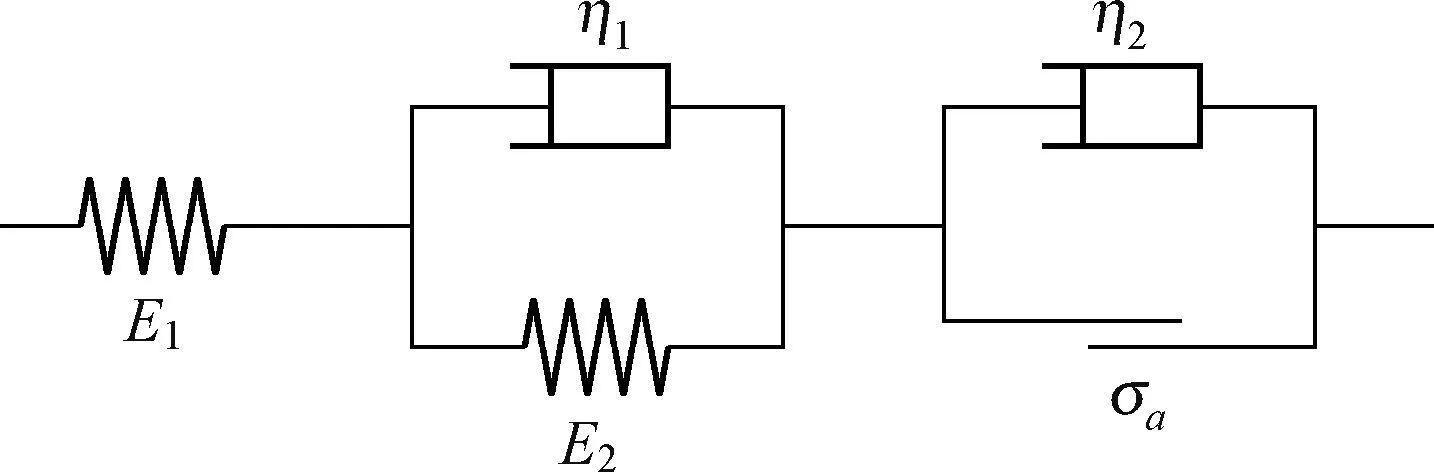
图4 西原模型

由图4可知，总应变ε可以表示为：

ε=εe+ενe+ενp

(8)

式中，εe、ενe、ενp分别表示胡克体、黏弹性体、黏塑性体的应变。

分数阶蠕变的模型本构方程：

(9)

式中，E2表示盐岩的变形模量。

2.4 分数阶蠕变模型参数

本文采用分数阶蠕变模型，如图5所示。

由图5可知，盐岩的总应变ε由三个部分组成，分别为：胡克体的应变εe，黏弹性体的应变为ενe，黏塑性体的应变为ενp。

图5 分数阶蠕变本构模型示意图

总应变ε可以表示为：

ε=εe+ενe+ενp

(10)

分数阶蠕变的模型本构方程：

(11)

图6 不同盐岩蠕变模型的拟合曲线(轴压为31.46 MPa)

表2 盐岩蠕变模型参数

E1/ MPaE2/ MPaη1η2βγC1C2C3Bailey-Norton2035———————————————0.00230.0032-0.608Burgers模型145124421.879×1053.69×104———————————————西原模型145024453.685×1047.461×104———————————————分数阶蠕变模型1718———74932.682×1050.3910.981—————————

3 蠕变模型对比分析

通过使用Origin对轴压31.46 MPa的蠕变试验进行非线性拟合，得到各个模型参数的拟合结果，见表2。并将拟合得到的参数代入轴压39.78 MPa的试验中计算蠕变变形，计算结果曲线如图7所示。对比计算结果与试验数据发现，在应力-应变范围相差不大时，其蠕变模型参数也变化不大，从图7可以看出：Bailey-Norton模型、Burgers模型、西原模型、分数阶模型的计算结果与蠕变试验数据均较为接近，且分数阶模型拟合效果更加明显。随着时间t的增加，分数阶蠕变模型的曲线与蠕变试验曲线重合。

图7 不同盐岩蠕变模型的计算结果(轴压为39.78 MPa)

由图7可知，各个模型在瞬时蠕变应变的计算结果能够较好的匹配试验数据；当进入稳态蠕变阶段时，随着时间t的增加，Bailey-Norton模型、Burgers模型、西原模型曲线均远离试验结果曲线。由于分数阶蠕变模型考虑了盐岩蠕变损伤引起的粘性随时间的变化[3]，因此，在稳态蠕变阶段后期，能够较好的接近试验数据。