《九章算术》的模型化思想——以“方程模型”为例

王斌儒 甘肃有色冶金职业技术学院 建筑与信息工程系

模型化思想产生于中国古人的社会实践之中，体现着中国古代的生产方式、生活方式和思维方式的特点。在中国古代数学典籍中蕴涵着中国古代数学模型化思想的发展历程。

1 九章算术的概况

1.1 《九章算术》的起源与基本内容概说

秦汉时期，中国古代的科学体系和教育体系才逐渐形成，数学表达逐渐体系化。《算数书》和《周髀算经》对数学思想系统产生了重大影响。大约在这个时期，《九章算术》成书，关于具体时间以及著者等问题，长期以来莫衷一是。李迪指出《九章算术》是刘徽所著。现在我们所说的《九章算术》即是刘徽的版本。

刘徽的《九章算术》，全书一共包括九个部分，分别为方田、粟米、衰分、少广、商功、均输、盈不足、方程和勾股。前面六章分别是数学在社会生活的不同领域中的应用，后面三章提供了可用于各个领域的三种常用数学模型，每章都通过具体问题来表明这种应用。《九章算术》中九章的内容详情见表1。

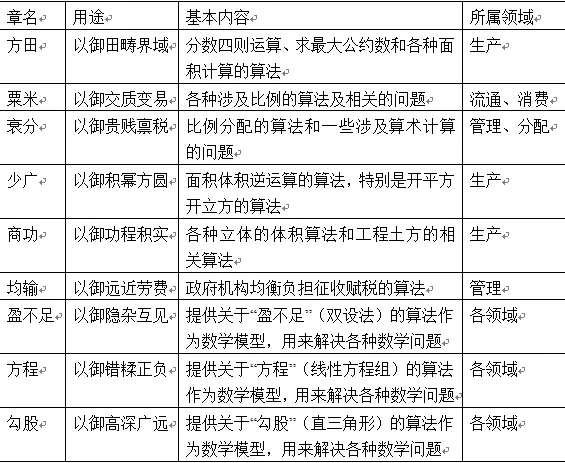
表1 《九章算术》九章的内容

《九章算术》作为中国最早给出系统的数学模型的著作，为实际生产生活中的问题提供了新的方法和思路。《九章算术》明确地以应用为目的，解决人们日常生活、生产实践的诸多问题，数学模型化思想渗透其中，密切联系实际，将现实生活中的一般现象概括为数学问题加以解决。

1.2 《九章算术》的历史地位

《九章算术》是古代最重要的数学典籍之一，历史上多次作为朝廷颁定的首选数学教科书使用，对中国古代数学和数学教育的发展起了巨大的作用，是中国古代数学从汉代直到元代前期一直处于世界数学的前列的基础。

2 《九章算术》的模型化思想

数学模型是为了解决现实世界问题而建立的，数学模型是人们认识原型的方式之一。结合方程，构建数学模型数学应用问题是包含了一个或多个数量关系的具体情节或事件，解决数学应用问题的过程就是从情节中抽象并理顺数量关系的过程，方程是有效地表达、处理、交流和传递信息的工具，是反映客观事物数量变化规律的一种模型。数学应用问题可以以方程为途径，构建数学模型来解决，在这种情况下所构建的就是方程模型。

《九章算术》做了许多属于建立和使用数学模型的工作。它的“九章”内至少有三章——盈不足、方程、勾股——提供的就是基本的数学模型。下面主要以“方程模型”为例阐述《九章算术》的模型化思想。

2.1 九章算术》中的“方程模型”

《九章算术》中的“方程”，实际是线性方程组。“方程术”解线性方程组的方法是世界上最早的完整的线性方程组解法。现今矩阵变换中的一些性质：对方程组的增广矩阵进行初等变换不改变方程组的解，对矩阵施行初等变换不改变矩阵的秩等，在方程术及刘徽注中都有其理论依据。

刘徽对“方程”的注释为：“程，课程也.群物总杂，各列有数，总言其实，令每行为率.二物者再程，三物者三程，皆如物数程之，并列为行，故谓之方程.行之左右无所同存，且为有所据而耳.”这段文字是刘徽对“方程”概念的精辟解说。在《九章算术》第八章方程中共计18 个题，二元的8 题，三元的6 题，四元、五元的各2 题。在题中涉及方程的矩阵表示和直除法消元每一题都是借助于算筹进行“遍乘直除”。所谓“遍乘”就是用常数乘某一行中各数；所谓“直除”就是要消去乙行某未知数系数，使用甲行同一未知数的系数乘乙行所有的数，然后用甲行一次次对减乙行，直至乙行该系数为零。其实这里的“遍乘直除”基本想法和后面的矩阵解线性方程组想法是一致的。

“遍乘直除”法是把此“方程”前三行转化成只有反对角线上有非零元，从而求得解答。如果将方程组系数的方阵横着写，就是现行教材中线性方程组系数的增广矩阵，筹算过程就是现行矩阵的行初等变换。然而由于当时筹算过程的程式化与机械化，需要多次反复的演算，使得筹算过程相当繁琐，并且又由于受到直除是以少行减多行的限制，常常使变换无法施行。但正是基于这种程序化的演算，才出现了小数“直除”大数的情形，从而促进了负数的产生和正负数加减法法则的形成，随之变换过程得以施行且越来越简捷。

2.2 《九章算术》中“方程模型”理论的意义

以特定的数学模式代替各种数学关系的分析，这种思想与方法在我国古代数学中有着非常深远的影响。“方程”这一数学模型，便是这一思想发展的产物 。“方程术”以及由此所进一步发展的演算程序化，使我国古代解方程组法达到了相当完善的领先水平。

在对“方程”施行直除变换时，要求是以少行减多行，而这个限制常常使得方程术无法畅行。正是由于这种“并减之势不得广通”，与“方程”解答程序相矛盾，导致了正、负数的产生，从而又推动了方程术的发展和完善。《九章算术》中正负术曰：“同名相除，异名相益，正无入负之，负无入正之。其异名相除，同名相益，正无入负之，负无入正之。”前一半给出了正、负数的“减法法则”，后一半给出了正、负数的“加法法则”。

《九章算术》关于负数的记录在世界上也是首创的，因为在外国，印度在七世纪、欧洲人在十三世纪才开始认识负数。

3 总结与反思

本文通过对《九章算术》中模型化思想的研究，重点分析了卷第八方程中的数学模型思想的应用，从《九章算术》可以看得出，中国数学文化起源于人的实际需要，比如丈量土地、测量容积等。它以社会生活与生产实际为研究对象，以解决实际问题为目标，围绕建立算法与提高计算技术而展开，强调在观察、实验基础上进行分析、归纳得出结果，寓理于算，把数学建立在实际直观模型的基础上。在九个章节中后三个是数学模型，本文挑选出方程模型作为例子，是因为方程定理是中国几何的根源.由此看来，刘徽定义的“方程”相当于现在的方程组。由于本人精力和水平的有限，对分类的认识可能不够到位，汇总也不能十分完全，而且对于“盈不足”模型和“勾股”模型并没有具体分析，这些还可以作进一步的改进。